解析概率基础在《生物统计学》中的重要作用

朱贵凤

(天津现代职业技术学院，天津 300222)

一、生物统计学的内涵

生物统计学在生命科学的研究以及生产实践中起着非常重要的作用，生物统计学是集科学的实践性、以及科学的应用性还有方法论于一体的一门学科，应当明确的是，生物统计学的重要任务之一是应用于实践。凭借统计推理的能力，学会从不确定性和概率的角度认真思考问题，深刻理解统计学的所有基本原理。在科学实验中，统计学原理的应用更为突出。因此，我们说生物统计学是数理统计在生物学研究中的应用，它结合数理统计原理和统计方法，来理解、分析、推断和解释生命过程中的各种现象和各种实验调查数据。它属于应用数学领域。它不仅为设计实验和收集数据提供了正确的手段，而且生物特征识别能够给出真实客观的科学结论。生物数学包含了许多分支，其中生物特征学是最早形成的分支之一，其核心是运用统计学原理和方法研究生物客观现象和问题，在这样的过程中形成一门新的学科，即生物数学。由于各种问题需要对生物学进行深入研究，这极大地促进了统计学在许多基本方面的发展和完善。统计方法在生物学等领域的应用，对于正确理解、正确推断和正确解释生命科学中的各种定量现象，在生物学界显得越来越重要。统计分析和实验设计是生物科学研究中不可分割的两个部分。统计分析的原理和方法是实验设计的基础。正确设计的实验为统计分析提供了更丰富、更可靠的内容信息，二者紧密结合，得出科学合理的结论，不断推动应用生物学研究的快速发展。因此，生物统计学是人类不可缺少的一门重要学科。可以简单概括为：生物统计学主要包括生物统计学语言、生物统计学数据描述、生物统计学分析工具、概率基础和统计方法。下面重点介绍概率基础在生物统计学中的重要应用。

二、概率基础在生物统计学中的应用

概率基础主要包括：随机试验、随机事件、概率的统计定义、小概率原理、随机变量、随机变量的概率分布等。它们是如何应用于生物科学的？

(一)随机试验

随机试验是指在同一条件下观察某种生物现象的一种试验，当然包括各种科学试验。比如：新冠病毒在全球范围内肆虐，目前还没有完全被人类制服而且控制住，要控制好这场疫情，疫苗起到了至关重要的作用，全球都在进行大规模的试验，研究开发疫苗。这些就需要进行随机试验。

(二)随机事件

在人类进行的各类社会实践中有些现象在一定条件下必然发生，或不可能发生。例如，太阳会从西边升起,鱼儿离开水不能存活下去。他们分别称为不可能事件和必然事件。然而在生物科学中大量存在的，却是在一定条件下可能发生也可能不发生的现象，又例如，某人感染了新冠肺炎病毒，过马路恰好遇到了红灯，等等，这些有可能发生也有可能不发生的现象叫随机事件。

(三)概率的统计定义

1．在同一条件下进行n次重复试验，如果随机事件A发生了m次，其比值m比n称为随机事件A发生的频率，当实验次数逐渐增大时，随机事件A的频率越来越稳定地接近某一数值P，那么就把P称为随机事件A发生的概率，这样得出的定义就是概率的统计定义。

例如，某大型孵化室记录了某品种动物8批入孵种蛋的孵化结果，见下表。

从上表可以看出，8批次孵化率围绕一个稳定值A=0.965做小幅摆动。而这个稳定值又无法准确地确定。在实际生活中用它们的加权平均数作为孵化率，来评价种蛋质量和孵化技术的好坏，这就是概率基础在生物科学的应用。

又例如，全球都在研究治疗新冠肺炎的疫苗，目前国内至少有四家公司在研究生产疫苗，世界上多个著名大学和生物制药公司合作开发疫苗。但是大家都在关注疫苗成功的概率是多少？

2．古典概率

若随机试验满足：随机事件的总数是有限的，每个随机事件出现的可能性相等，称为古典概率。

例：某社区有40人报名参加防疫志愿者服务，其中有党员25人，志愿者分为4个小组，(每组10人)，现在要挑选一名志愿者，求下列概率：(1)选到的志愿者是第一组的同学，(2)选到的自愿者是党员

解 设A={志愿者是第一组的}，B={志愿者是党员}

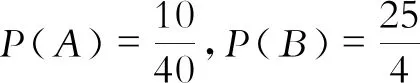
生物统计学中概率基础的一个有趣的例子就是对男性和女性出生率的研究。传统的看法是男孩和女孩出生的比例约各占50%，但事实是男孩比女孩更容易出生。法国数学家拉普拉斯在其著作《概率论的哲学探索》中，根据法国的研究资料，研究了男孩或女孩的出生的概率问题，经过近10年的统计研究，法国每个地区出生的男女人数之比总是在一定数值比摆动，为了找出问题所在，拉普拉斯选择巴黎对这一地区进行实地调查实验，研究发现该地区出现了“重女轻男”的现象，这与中国的“重男轻女”不同，由于自然因素的影响，必然会影响统计规律。人们不禁要问，为什么男孩比女孩多一点？拉普拉斯从概率的角度解释了这个问题，因为带有X染色体的精子和带有Y染色体的精子与卵子交配的机会并不完全相同。这也说明了概率论基础知识在生物学中的广泛应用。

(四)小概率原理

在统计学中，小概率事件的概率通常界定在小于0.05或0.01之间,这称为小概率原理。小概率原理已在生物统计学上进行科学检验中得到广泛的应用。在后疫情时期，虽然我们周边得新冠肺炎的病人几乎没有，也可以说现阶段在我国，我们得新冠肺炎的概率属于小概率事件，但是我们仍然不能掉以轻心麻痹大意，我们还是要求人们在公共场合戴口罩，尤其是乘坐交通工具时戴口罩，不聚集，勤洗手，常通风等等。某种意义上讲概率基础知识在科学防控上意义很大。

(五)随机变量

在生物统计学中每次做的随机试验的结果至少有两种可能。若用字母x表示一次试验可能发生的结果。那么x的取值范围就应该是数值0.1.2.....或者某一区间(a，b)。究竟会出观什么结果当然是随机的。我们称这样的x为随机变量。

例如：用某种新冠肺炎疫苗给10名感染新冠肺炎的病人注射后，其痊愈的可能结果是“0人痊愈”、“1人痊愈”、“2人痊愈”……“10人痊愈”。若用x表示痊愈人数，那么x的取值为0，1，2，……，10。

例如：测定某位新冠肺炎患者感染的病毒数，x表示测定结果，则x的取值结果就是0，1,……。

例如：测量某个成年者的体重，表示测定结果的变量x所取的值为一个范围(a，b)，x值可以是这个范围内的任何实数。

又例如：测量灯泡的寿命，x表示测定结果，则x可能取值为(a，b)内的任何数值。

(六)随机变量的概率分布

随机变量的概率分布是生物统计学概率基础中一个非常重要的基本概念。所谓随机变量的概率分布，是指对所有可能的随机试验结果和所有可能结果发生的概率的描述，以及对所有可能的随机试验结果的研究，以揭示生物世界存在的统计规律，这也是随机变量概率分布的重要作用。其中，二项分布是离散型随机变量最常见的分布，正态分布是连续型随机变量最常见的分布。作为概率论基础上的两个重要概念，它们是生物统计学研究中不可缺少的重要内容。

1．二项分布

设X示事件A发生的人数，

故称X服从参数为n,p二项分布。记为X～B(n,p)，其中n,p称为参数

例如：某国高风险区感染新冠肺炎的概率为0.7，求在这一地区检查10人，恰有3人

感染新冠肺炎的概率。

设X表示检查10人感染新冠肺炎的人数

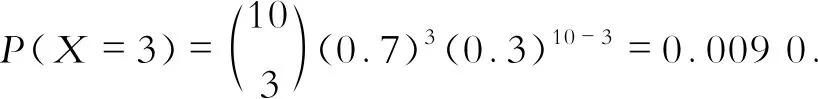
2.正态分布

正态分布就是指的是一种大多数变数都集中在平均数附近，由平均数向两侧分散的变数逐渐减少的连续型概率分布。其分布密度曲线是一条光滑的型似于座钟的曲线，是一条对称而且连续的曲线。在生物统计学的理论研究和实际应用中，概率基础的正态分布起着重要的作用。在人类社会科学中，许多变量服从或近似服从正态分布，如动物的日增重、产蛋率、产奶量、产毛量、乳脂率、瘦肉率、体型指数、某些生理指标等，以及人的身高、体重、体重等，血液粘度指数等等也服从或近似服从正态分布。实验误差和我们班上学生的数学成绩也近似服从正态分布。在人类社会实践中，许多概率统计分析方法都是基于正态分布的。

注意：一般正态分布的分布函数F(x)与标准正态分布的分布函数Φ(x)之间的关系为

于是：

比如：一群山羊的体重X～N(100,400),试计算该群山羊体重在80～120 kg范围内的概率。

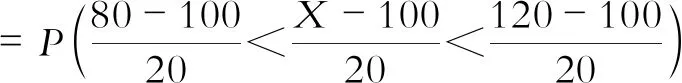
=Φ(1)-Φ(-1)

=2Φ(1)-1

=2×0.8413-1

=0.6826

即该群山羊体重在80～120 kg范围内的概率为0.682 6这就是运用概率统计方法研究生物科学的实际应用。

三、概率基础在新冠肺炎科学防控中的应用

新冠病毒在全球肆虐，目前还仍然没有得到完全控制。众所周知：要控制好这场疫情，疫苗起到了至关重要的作用，以色列的一项研究已经显示，在大规模接种新冠疫苗后，以色列的疫情防控取得了显著效果，成为海外第一个通过接种疫苗成功遏制疫情的国家。全球都在关注疫苗成功的概率是多少？

我们需要了解一下疫苗的原理：疫苗就是基于特异性免疫机制，所谓特异性免疫具有相当的专一性它只针对特定的外来异物发挥免疫作用。当病毒进入人体后，用它表面的特殊结构穿过细胞膜，在细胞中大量复制，复制出新的病毒去感染其他健康的细胞，迅速地人体内的免疫细胞就会很快地发现这些病毒。疫苗的生产过程是,首先，科学家从病患的身体上分离出毒株，经过体外细胞培养，使病毒株大量复制增值，最关键的一步是将这些毒株用科学方法进行灭活处理，使他们失去原有的致病性，然后将失去毒性的病毒少量的放入人体内，人体就会产生抗体，疫苗除了直接注射灭活的抗原，让机体自然产生抗体以外，还有一种是直接注射抗体，这两种的作用都是一样的，他们都使人体不再容易感染到病毒。

目前世界很多国家都在研制疫苗，我国也有多家公司在研制疫苗，疫苗成功的概率达到99%以上，远远高于其他国家疫苗的成功率。

通过概率统计研究有如下的数据表明：在单针接种后28天，陈薇团队研发的克威莎疫苗三期临床试验结果，该疫苗的总体保护效力达到了74.8%，美国强生公司研发的也是单针疫苗，尽管都同处于三期临床试验，但总体保护效力仅有66%，不过都高于世卫组织规定的50%。在单针接种后28天陈薇团队研发的克威莎疫苗针对重症病例的保护效力则达到了100%。美国强生公司疫苗针对重症病例保护效力为85%。见下图表：表-1.表-2

表-1

表-2

由表-1.表-2知：“从疫苗保护作用来看美国强生公司的疫苗明显低于陈薇团队研发的克威莎疫苗数据，从而说明了陈薇团队研发的疫苗的效果会更好。”这也体现了概率基础在科学防控方面起到了重要作用是生物科学最直接的应用。

综上所述：概率基础在生物统计学中有着重要的作用，它的应用无处不在,它在我们人类的生活中给予了最具应用的广泛性和实践性，尤其在现在为我们抵御病毒侵害提供最有力的理论依据，为科学防控打下坚实的科学基础。