一类约化的 Rosenzweig-MacArthur 随机捕食者-食饵模型的平稳分布
杨亚飞
(西北师范大学 数学与统计学院,甘肃 兰州 730070)
0 引言
捕食者与食饵种群间的相互作用是生态系统的重要组成部分[1]. 自20世纪20年代Lotka和Volterra首次提出Lotka-Volterra模型以来,越来越多的学者通过构建各种模型来研究种群间的相互作用[2-3],其中之一就是下面的Rosenzweig-MacArthur模型
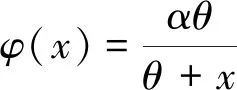
另一方面,功能反应是影响捕食者-食饵模型的重要因素.2013年,Dawes和Souza推导出一个新的三维模型和不同类型的功能反应,包括Holling型功能反应等[4].根据他们的方法和文献[5]的理论,Lax等在文献[6]中提出了下面的模型:
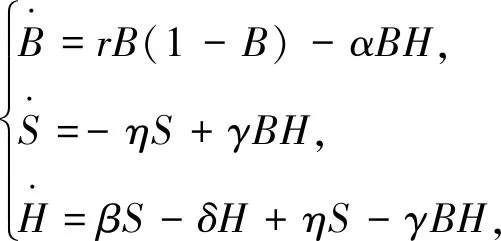
(1)
其中:S代表休息的捕食者;H代表狩猎的捕食者.所有的参数均为正数.
对类似于模型(1)的这种常微分方程模型,它并不能捕捉环境的波动.因此,越来越多的学者将随机干扰项引入捕食者-食饵模型中[7,8].基于此,本文考虑如下随机模型:
(2)
其中:σi(i=1,2,3)表示噪声的强度;Bi(i=1,2,3)是相互独立的标准布朗运动,其定义在带有滤子{Ft}t≥0且满足通常条件的完备概率空间(ω,F,{Ft}t≥0,P)上.
1 预备知识
为便于证明本文的主要结论,令
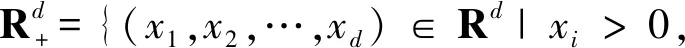
定义[9]如果函数P(s,x,t+s,A)与s无关,则转移概率密度函数P(s,x,t,A)是时间齐次的(且相应的Markov过程称为是时间齐次的),其中0≤s≤t,x∈Rd,A∈B,B表示Rd中Borel集的σ-代数.
令X(t)是Rd中标准的时间齐次的Markov过程,且满足
dX(t)=F(X(t))dt+G(X(t))dB(t),
(3)
其中F(X(t))和G(X(t))分别是n维向量函数和n×m阶矩阵.
定义算子L和X(t)的扩散矩阵A(x)分别为:
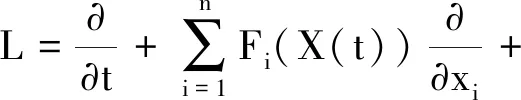
引理1[9]假设X(t)满足(3)且函数V(x(t))∈C2,1(Rn×R,R),则
dV=LV(X(t))dt+VxG(X(t))dB(t),
其中,
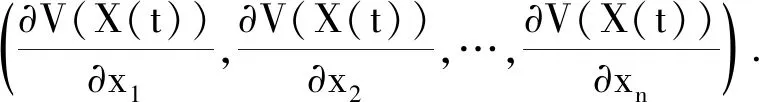
引理2[9]假设存在有界开集U∈Rd且U带有正则边界Γ,若满足以下两个条件
(A1):对任意的x∈U,扩散矩阵A(x)是正定的.
(A2):在RdU上,存在非负的C2函数V,使得LV<0.
则Markov过程X(t)存在唯一的平稳分布,且分布具有遍历性.
2 主要结果
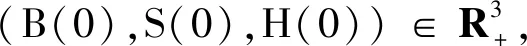
证明显然,系统(2)的参数满足局部Lipschitz条件,由文献[10]知,当t∈[0,τe]时(τe为爆破时间),对任意给定的初值(B(0),S(0),H(0)),系统(2)存在唯一解.为使定理成立,只需证τe=∞.进一步由文献[11],只需证τ∞=∞几乎必然成立.反设不真,则存在正常数T和ε<1,使得
P{τ∞≤T}>ε.
因此,存在整数n1≥n0,使得对任意的n≥n1,有
P{τ∞≤T}>ε,
其中n0由文献[11]给出.
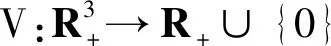
其中a将在后续证明中给出.
由引理1可得
其中


定理的后续证明与文献[11]中定理3.1的证明类似,故在此省略,从而定理得证.
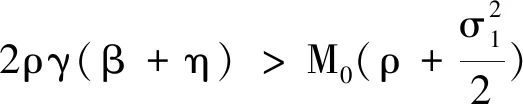
c=γ(β+η).
证明系统(2)的扩散矩阵为
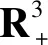
下证(A2)成立.通过计算可得

(4)
令
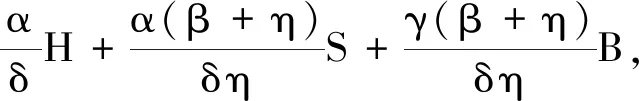
由(4)得
(5)
再令

(6)
定义
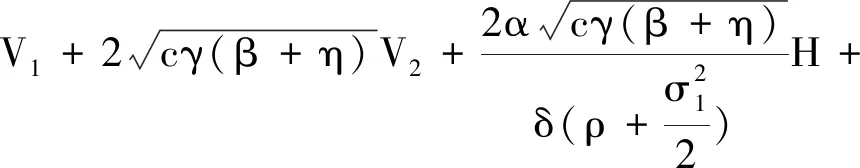
由(5)和(6)得
其中
然后定义
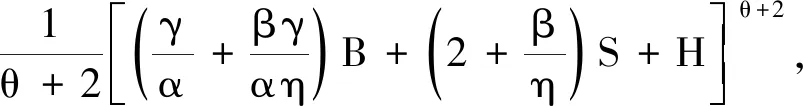
则
其中
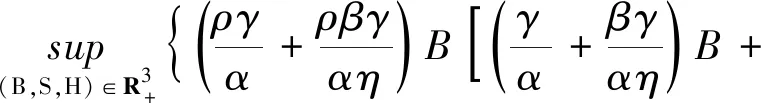
现定义如下Lyapunov函数
其中N充分大且满足:
-Nλ+D1≤-2.
通过计算得
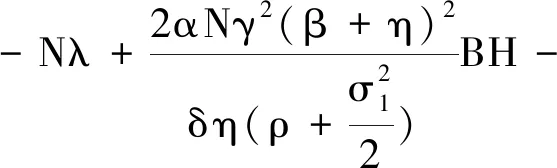
(7)
为了验证条件(A2),定义一个有界开集
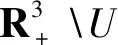
(8)
(9)
(10)
(11)
(12)
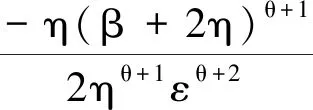
(13)
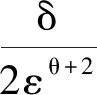
(14)
其中
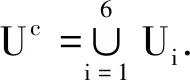
(ⅰ)对任意的(B,S,H)∈U1,注意到xb-bx+b-1≥0,由(8)和(9)得

(ii)对任意的(B,S,H)∈U2,由(9)和(10)得

另一方面,由(7)得
(iii)对任意的(B,S,H)∈U3,由(11)得
LV≤
类似地,对任意(B,S,H)∈Uj(j=4,5,6),由(12)、(13)和(14)可得LV≤-1.
因此,对任意的(B,S,H)∈Uc,有LV≤-1.这说明条件(A2)成立.定理得证.
3 数值模拟
本节将采用文献[12]中的Milstein高阶方法来对理论结果进行数值模拟.选取系统(2)的初值为(0.1,0.2,0.2),其余参数如表1所列.

表1 系统(2)的各参数值
利用Milstein高阶方法可得到系统(2)的离散化变换为
其中:时间增量Δt>0,εi,j(i=1,2,3)表示互相独立的高斯随机变量,遵循分布N(0,1).
通过计算发现
即定理2的条件成立.因此,由定理2可知,系统(2)存在唯一的平稳分布且其具有遍历性.系统(1)、(2)的解及其种群密度函数的直方图如图1~图7所示.

图1 系统(1)和(2)中食饵种群B的解曲线
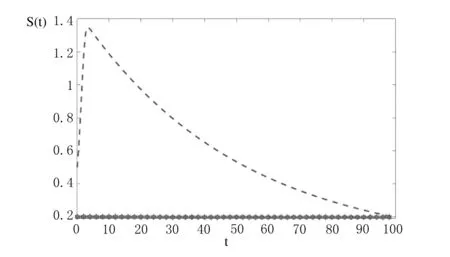
图2 系统(2)中休息捕食者种群S的概率密度函数直方图

图3 系统(1)和(2)中捕食者种群H的解曲线

图4 图2的局部放大图
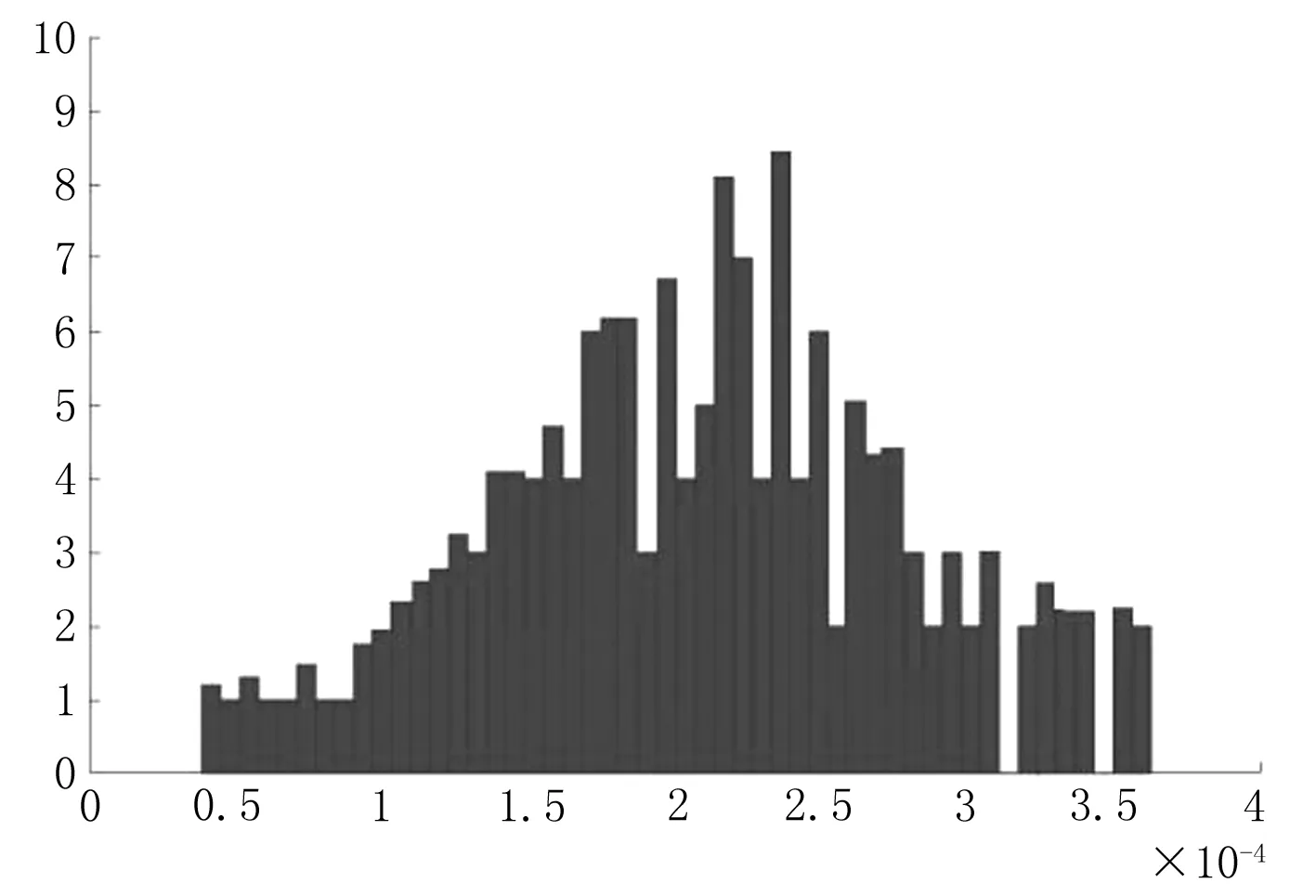
图5 系统(2)中食饵种群B的概率密度函数直方图
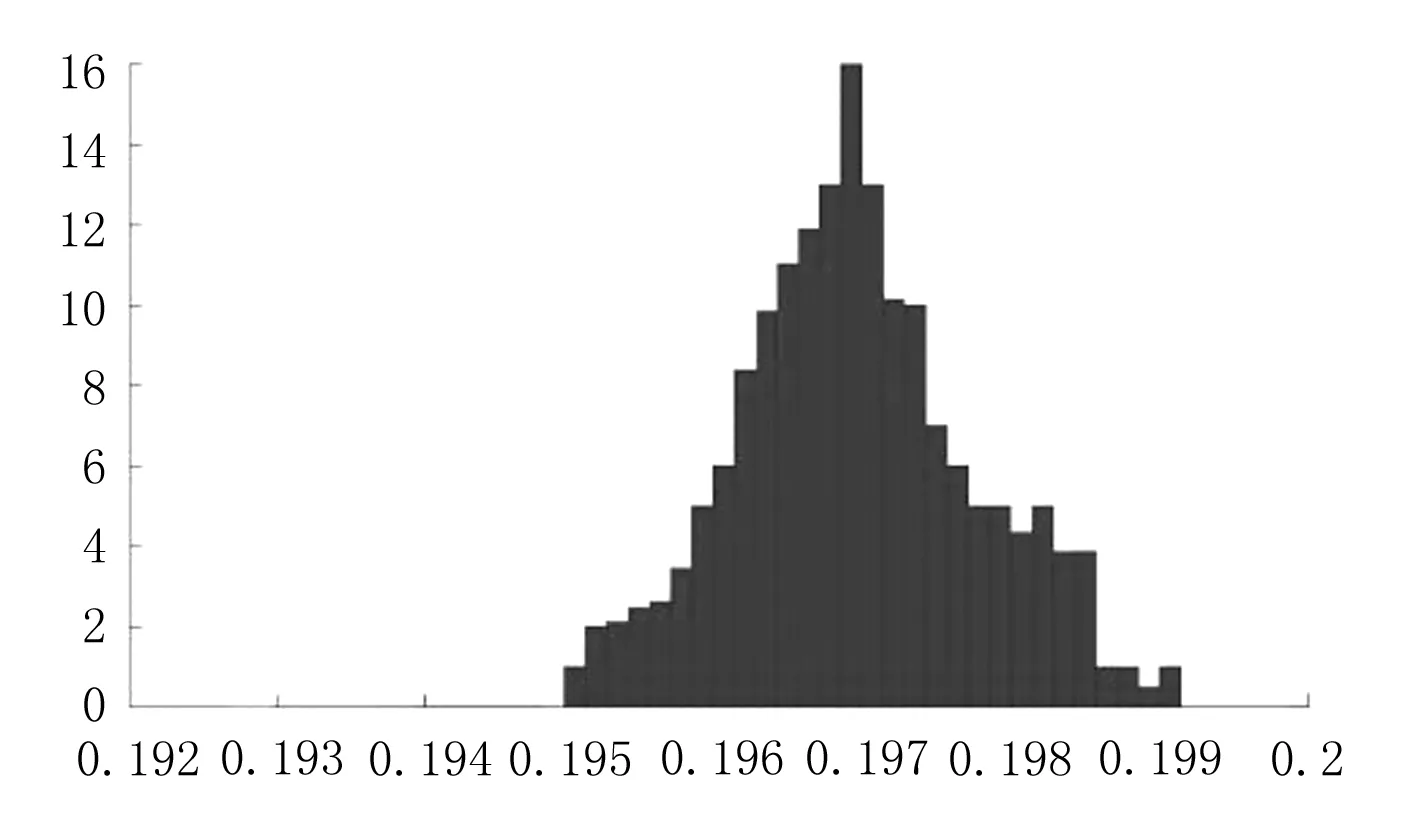
图6 系统(1)和(2)中狩猎捕食者种群H的解曲线
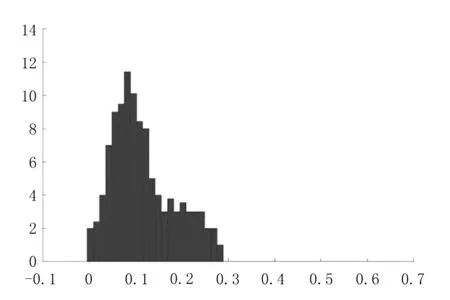
图7 系统(2)中狩猎捕食者种群H的概率密度函数直方图
4 结论
本文利用随机微分方程理论,通过构造合适的Lyapunov函数来分析一类约化的Rosenzweig-MacArthur模型整体正解及其平稳分布的存在唯一性.定理2表明,当系统(2)的参数满足一定条件时,系统(2)会存在唯一的平稳分布并具有遍历性.

