一个二分量Camassa-Holm系统解的爆破准则

黄 群

(温州大学数理学院，浙江温州 325035)

旋转的二分量的Camassa-Holm系统[1]如下所示：

若σ=1，该系统就是经典的二分量Camassa-Holm系统[2-4]：

这个系统是完全可积的．

文献[1]通过线性传输理论建立系统（1）柯西问题的局部适定性，基于特征方法和Riccati型微分不等式研究了系统（1）在情况下的爆破准则．受文献[1]启发，本文考虑系统（1）在情况下的解爆破的条件．当时，系统（1）变成如下形式：

通过证明得到，初值在一定的空间条件中，系统（4）的解发生爆破当且仅当它的一阶导数趋于无穷．此外，给出了系统（4）发生爆破的初始条件．

1 准备知识

介绍一些符号和属性．用∗表示卷积，Lebesgue空间中的范数表示为其中1≤p＜∞．L∞(R)包含了所有的本性上确界函数，若f为Lebesgue可测函数，其范数为为了定理证明，引入特征方法．设q(t,x)是随着解u(t,x)发展的粒子轨迹，并且满足方程

通过计算可得以下与时间无关的守恒量，记为：

2 爆破准则

考虑系统（4）的初值在一定条件下，系统的相应解发生爆破的充要条件，即解发生爆破的准则．利用反证法进行证明，关键在于估计如果得到有界，则产生矛盾．

时，(u,)ρ在有限时间内爆破．

证明：为了方便运算，把系统（4）改写为如下形式：

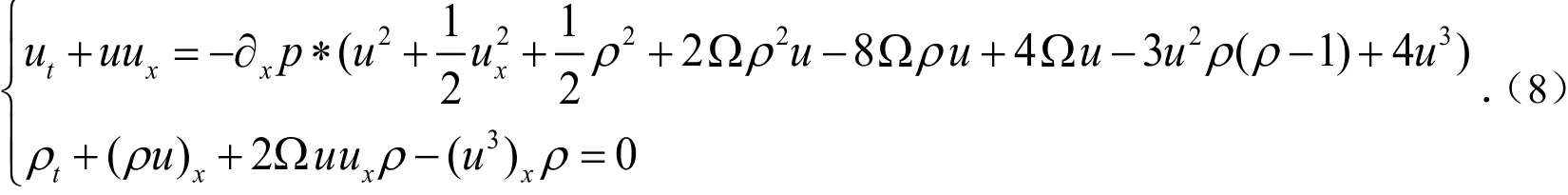
利用这些符号，相应地可以把（6）式改写为如下形式：

假设T＜∞，（6）式不成立，则存在一个正数A，使得

对任意x∈R，有以下式子成立：

接下来我们估计函数f的上确界．

另一方面，可以得到以下估计：

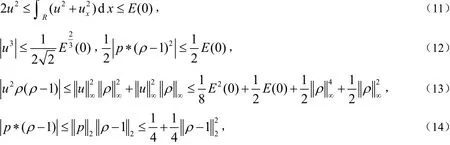
其中常数C和C1只依赖于

给定任意x∈R和引入一个新的一阶微分函数

满足

现说明P(t)≤0，t∈ [ 0,T)．如果不成立，则存在一些t0∈[0,T)，使得P(t0)＞0．令t1=max{t＜t0;P(t)≤ 0}，则P(t1)=0，P′(t1) ≥ 0，或等价于

和

同时有：

这与（22）式矛盾．因此有P(t)≤0， ∀t∈ [ 0,T)．所以任意选择x∈R，t∈ [0,T)，有

接下来考虑系统（4）的解爆破的充分条件．先介绍一个对证明爆破准则有重要作用的引理．

引理1[5]令那么对 ∀t∈ [0,T)，至少存在一个点ξ(t)∈R，使得函数m(t)在(0,T)中绝对连续，且有在(0,T)上几乎处处成立．

下面给出系统（4）的解发生爆破的初始条件．

证明：由稠密性知，只要证明定理对s≥3成立即可．注意到系统（4）的第二个方程对x求导得：

进而可以得到以下估计：

从而有：

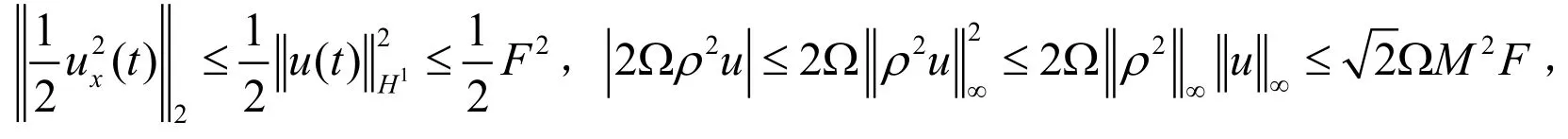
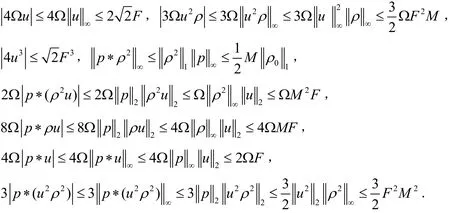
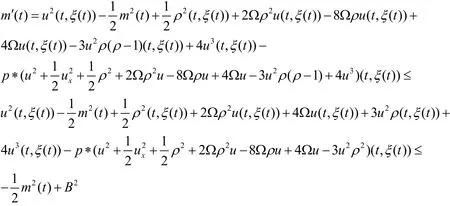
在[0,T)几乎处处成立．