求解奇异线性系统的右预处理GMRES方法

王帅丽

(温州大学数理学院，浙江温州 325035)

本文讨论求解线性方程组：

本文用T A表示A的转置，Ir为r阶的单位矩阵，用R()A和N()A分别表示A的值域和A的零空间．

本文主要讨论奇异线性系统的右预处理GMRES（The Generalized Minimal Residual）方法并做收敛性分析．众知，矩阵乘法不满足交换律，尤其是奇异矩阵乘法逆序律的复杂性，导致左、右预处理系统的系数矩阵其条件数有时候差异很大．从而，对某些问题，若做左预处理效果不理想时，可以考虑做右预处理[1-2]．

由Saad等[3]提出的GMRES方法是解决大型非对称线性系统最流行的方法之一，用GMRES方法可以进行求解非奇异线性系统，也可以求解奇异线性系统[1,4]．

定义1[5]设B∈Rn×n，我们称满足r(Bi)=r(Bi+1)的最小非负整数i为B的指标，记作：

B的Drazin逆记为BD，并满足：

定义2 对于任意矩阵A∈Rn×n，如果R(A)=R(AT)，那么称A为值域对称矩阵．

引理1[6]设A∈Rn×n，那么值域对称矩阵的等价描述如下：1）R(A)=R(AT)，2）N(A)=N(AT)，3）A+A=AA+，4）A+=A#，其中A+是A的Moore-Penrose广义逆，即A+满足：A+AA+=A+，AA+A=A，(AA+)T=AA+，(A+A)T=A+A．

A#是A的群逆，即A#满足：AA#A=A，A#AA#=A#，AA#=A#A．

如果A是值域对称矩阵，则A的指标为1，即index(A)=1，且；但index(A)=1，则A不一定是值域对称矩阵，如：

文[6]中Zhang对线性系统（1）的系数矩阵做了左预处理，而本文对线性系统（1）的系数矩阵做右预处理，使得预处理后的系数矩阵是值域对称的．对于值域对称的奇异线性系统，用GMRES方法进行求解时，具有良好的性能．因此，我们需要找出合适的预处理子使得经过预处理后系统的系数矩阵是值域对称的．除此之外，本文基于恰当分裂，讨论了其收敛性．

1 奇异线性系统的右预处理子

基于线性方程组（1）的系数矩阵A的分裂所诱导的分裂迭代方法，称为定常迭代法．对于系统（1）的系数矩阵，当A是非奇异矩阵时，基于A的分裂：A=M-N，假设M可逆，则其迭代格式为xk+1=M-1Nxk+M-1b，k=0,1,2,…，称M为预处理子；当系数矩阵A是奇异矩阵时，A-1不存在，因此奇异矩阵M作为预处理子更合理．经过右预处理后的矩阵使得预处理后的线性系统的系数矩阵是值域对称的，且 index(Aˆ)=1，然后用GMRES方法进行求解．

设用一个奇异矩阵M作为线性系统（1）的右预处理子，则通过它预处理后的系统为：

通过求解（3）来求解（1）．

定义3A的分裂：为恰当分裂．

注意：如果A和M是非奇异的，那么由A所诱导的分裂均为恰当分裂．

证明：先证明1）．

首先有

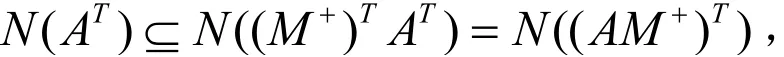
由N(A)=N(M)，则

由r(BM)≤r(B)，可得

再证2）．

首先有N(M+) ⊆N(AM+)，由1）可得

则

由N(M+)=N(MT)，可得N(AM+)=N(MT)．

证毕．

当原方程组的系数矩阵不是值域对称的，那么经过预处理后方程组的系数矩阵是否是值域对称的呢？或者当原方程组的系数矩阵是值域对称的，那么经过预处理后方程组的系数矩阵是否依旧是值域对称的呢？如下定理给出预处理系统的系数矩阵保持值域对称的充要条件．

定理2 如果A是值域对称矩阵，N(A)=N(M)，那么AM+是值域对称矩阵，当且仅当M是值域对称的．

证明：由定理1知，N((AM+)T)=N(AT)，N(AM+)=N(MT)．

由A是值域对称矩阵，则N(A)=N(AT)．又由N(A)=N(M)，有N(M)=N(AT)．则N((AM+)T)=N(AM+)，当且仅当N(M)=N(MT)．

证毕．

进一步，由如下定理说明对任一系数矩阵A，经恰当分裂后的预处理系统的系数矩阵均为值域对称的．

定理3 如果A=M-N是恰当分裂，那么AM+是值域对称的．

证明：由定理1知：N((AM+)T)=N(AT)，N(AM+)=N(MT)．由于A=M-N是恰当分裂，则R(A)=R(M)，N(A)=N(M)，N((AM+)T)=N(AM+)，即AM+是值域对称矩阵．

证毕．

引理2[7]对于线性系统（1）应用GMRES，初始迭代向量x(0)∈R(A)，如果A是值域对称的，那么GMRES在终止时决定的解为：x*=A+b．

定理4A=M-N是一个恰当分裂，对预处理后的系统（3）应用GMRES，初始迭代向量y(0)∈R(A)，那么GMRES在终止时决定的解为：x*=A+b．

由引理2知，若y(0)∈R(AM+)，则GMRES在终止时决定的解为：y*=(AM+)+b．

下证R(AM+)=R(A)，x*=M+y*=M+(AM+)+b=A+b．

再证(AM+)+=MA+．

由于A=M-N是恰当分裂，则R(A)=R(M)，N(A)=N(M)，R(AT)=R(MT)．

又由R(M+M)=R(MT)=R(M+)，则M+M是R(M+)上的正交投影．

同理，A+A是R(A+)上的正交投影．

远程教育理念核心在于实现教学过程中教师与学生的时空分离，此理念在节省教育资源，促进教育公平发展的同时，也使得学习过程更具自主和灵活，满足不同水平学生对教学内容的充分理解，即契合“掌握学习”理论的一般原理。慕课、微课以及雨课堂等迅速成长，成为当下教育信息化的重要方式。但简单地将传统课堂数字化网络化就能取得绩效是不切实际的。实现在线教育优势,教师核心素养是保证教学质量，实现信息化教育有效推进的重要因素。

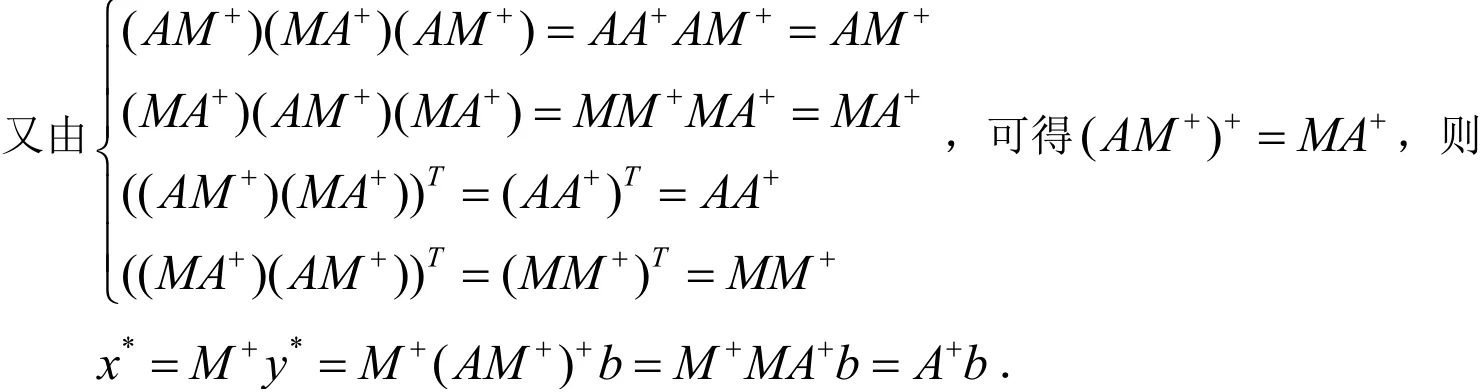
证毕．

2 恰当分裂的特征

由上节内容可知，对于任意一致的奇异线性系统，我们都可以基于恰当分裂的预处理GMRES方法得到广义逆解A+b，即基于恰当分裂选择预处理．在本节中，我们进一步讨论恰当分裂的特征及其它刻画，同时我们还讨论了恰当分裂条件下预处理系统系数矩阵的谱性质．

首先，R(A)=R(M)当且仅当存在一个非奇异矩阵P1使得M=AP1，N(A)=N(M)，当且仅当存在一个非奇异矩阵P2使得M=P2A．进一步，恰当分裂可由下述命题等价刻画．

命题1A=M-N称为A的恰当分裂，当且仅当存在非奇异矩阵P1,P2使得M=AP1=P2A．

线性系统（1）的系数矩阵A，A∈Rn×n，r=rank(A) ＜n，Berman等[8]通过下面A的分解来描述恰当分裂：

其中，A11是秩为r的非奇异矩阵，P和Q是置换矩阵．

引理3[8]A由（4）式给出，那么A=M-N是一个恰当分裂，当且仅当

其中，M11是秩为r的矩阵．

引理4[6]矩阵A由（6）式给出，那么A=M-N是恰当分裂，当且仅当

其中，R是一个秩为r的非奇异矩阵，且

引理5[9]矩阵A和矩阵M分别由（6）式和（7）式给出，那么

当线性系统（1）的系数矩阵非奇异时，假设M可逆，则A=M-N是恰当分裂，其迭代格式位：x(k+1)=M-1Nx(k)+M-1b，有如下经典结论成立：

进一步，当M不可逆时，有如下定理对这一结论加以推广．

定理5 矩阵A和矩阵M分别由（6）式和（7）式给出，A=M-N是恰当分裂，那么

证明：由A=M-N是恰当分裂，则N(A)=N(M)，N(AM+)=N(M+)，易证R(A+)=

令(λ,y)是AM+的特征对，则λ≠0，y≠0，故AM+y=λy≠0．

由N(AM+)=N(M+)，则M+y≠0，即

由于A+A是R(A+)上的正交投影，有

则

所以λ是的特征值，即λ是的特征值．

证毕．

3 结 论

通过GMRES方法求解奇异线性系统Ax=b，是目前解决大型稀疏线性系统最流行的方法之一．研究表明：A无论是不是值域对称矩阵，当找到预处理子M使得A=M-N是一个恰当分裂，则预处理后的系统的系数矩阵是值域对称的，那么GMRES将收敛到一个解；同时，x*=A+b是Ax=b在y(0)∈R(A)中的唯一解．在某种程度上，我们解决一个奇异的线性系统，就像解决一个局部的非奇异线性系统一样，或者用局部的非奇异化来求解一个奇异的线性系统．对于求解奇异线性系统，在恰当分裂条件下，我们已经推导出存在左预处理子使得R(M+A)=R((M+A)T)，存在右预处理子使得R(AM+)=R((AM+)T)．进一步，利用本文的理论结果，为寻求左、右全局预处理子P、Q使得提供了可能性，这也将是我们下一步的研究工作．