双重寻优的机器人轨迹规划及其在断路器柔性装配中的应用研究

舒 亮，葛亮君，吴自然，陈 威，张腾翔

(1．温州大学浙江省低压电器工程技术研究中心，浙江温州 325002；2．浙江聚创智能科技有限公司，浙江温州 325002)

断路器是配电系统中的重要保护性元件，在工业、民用等领域有广泛应用．目前断路器生产多以人工为主，自动化装配单元中柔性装配工艺缺失，装配流程复杂，只能完成单一规格产品的制造．工业机器人具有工作效率高、稳定可靠、重复精度好等优势，在制造行业得到了越来越多的应用[1]．将工业机器人与断路器自动化制造相结合，研究断路器柔性化制造工艺及其相应的机器人协调控制方法，对于提升断路器制造效率和产品品质具有重要意义．

机器人进行装配作业时，其运动轨迹对于机器人的作业效率和平滑稳定性能有较大影响，轨迹规划[2]是工业机器人运动控制的基础研究领域，决定着其作业效率和运动性能．李俊[3]、付荣[4]等采用4-3-4次多项式和3-5-3次多项式插值法研究了机器人轨迹规划问题，该类方法可以快速规划机器人末端的运动轨迹，然而仅适用于三段式轨迹，对于轨迹中间点发生变化的情况，无法适用．对于柔性装配机器人，机器人作业轨迹需要经过不同中间节点，可以采用三次样条插值法进行轨迹规划[5-6]，该方法计算量小，在一定优化算法的基础上，可以根据中间节点个数变化自发地对工作路径进行规划，适应性强．

群智能算法被较多用来对机器人轨迹规划问题进行研究[7-9]．通过群智能算法对机器人轨迹进行优化，一般需要设计相应的适应度函数或目标函数评判解的优劣性．马睿[10]等通过遗传算法对三次多项式插值的轨迹时间进行优化，根据目标函数将轨迹中每段时间相加得到的值进行比对得到优化结果，然而其优化解每次结果各不相同，得到的结果不稳定．类似地，冯斌[11]等人通过粒子群算法对点到点之间的高次多项式插值轨迹时间进行了优化，并采用适应度函数对解的优劣进行评价，但迭代结果在稳定性方面有待提高．王玉宝[12]等在对高次多项式轨迹优化过程中，通过动态调整学习因子改进了粒子群优化算法，改进后的算法性能有了一定提升，但由于该方法只对群体极值进行了优化，没有考虑粒子迭代过程中分段最优极值，因而优化的群体极值之外仍可能存在潜在更优解．

针对上述问题，本文提出一种双重寻优的机器人轨迹规划新方法，在适应度函数评判得到的优化粒子集合中，分别比对机器人每一分段轨迹对应的分段时间并进行二次寻优，从而得到机器人运动速度和加速度约束条件下的整体潜在更优解．在此基础上，研究并设计了一种适用于不同零件的断路器柔性化装配工艺，将改进的优化算法应用到机器人柔性化装配工艺中，并进行了相关仿真和实验验证．

1 柔性装配机器人动力学建模

1.1 断路器柔性装配工艺

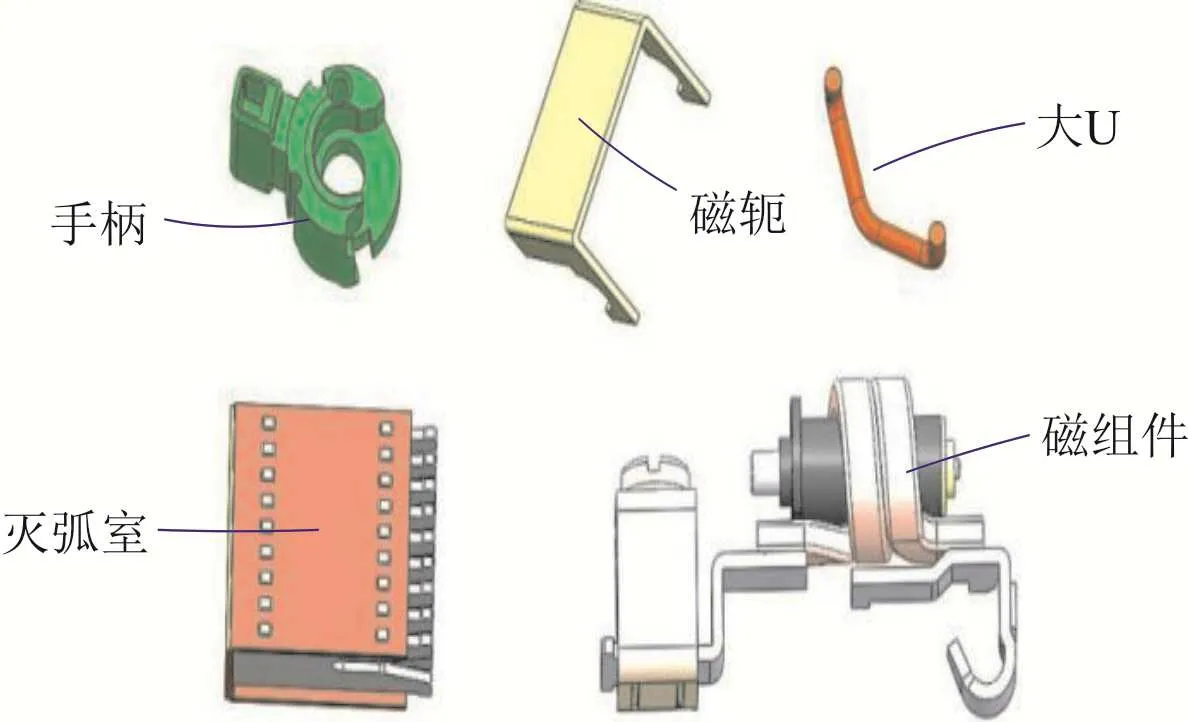
图1 断路器待装配零件模型

断路器的构成部件较多，以小型断路器为例，其主要构成有手柄、磁轭、大U、灭弧室和磁组件等，几何结构如图1所示．实现断路器柔性化装配，其关键在于对不同零件产生的随机姿态进行调整和归一化处理，需要进行零件姿态柔性化调整．图2所示为基于六轴机器人的断路器零件姿态调整系统，由六轴机器人、机器人末端夹具、姿态调整辅助机构和零件托盘组成，其中柔性机器人末端夹具由4个夹爪气缸组成，其结构如图3所示．通过夹头的设计使夹爪行程范围与零件尺寸相匹配，从而适用于不同姿态、不同零件的夹取和姿态调整．

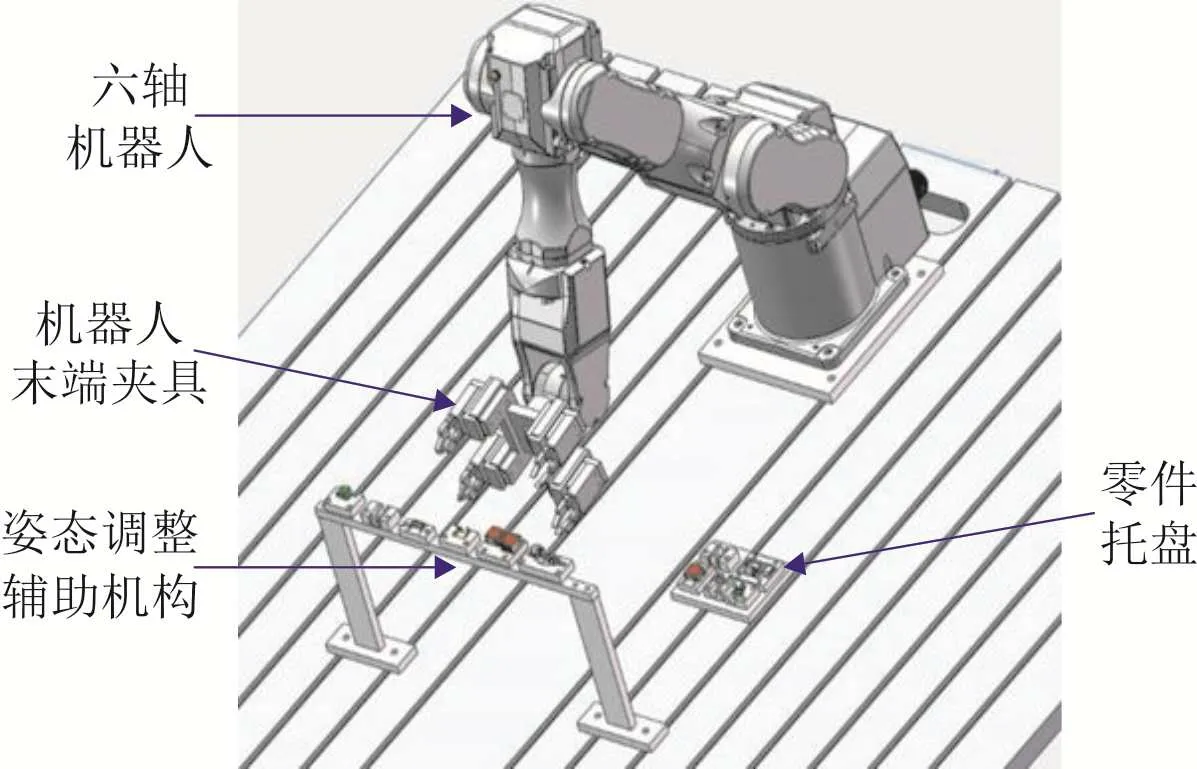
图2 基于六轴机器人的断路器零件姿态调整

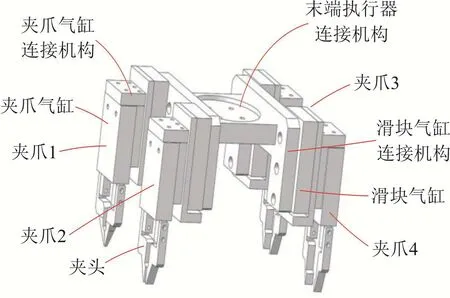
图3 柔性机器人末端执行机构示意图

断路器零件较多，为对姿态调整过程进行描述，选灭弧室其中一种姿态阐述柔性机器人装配过程．机器人末端夹具由4个夹爪组成，夹爪1到夹爪4行程分别为0 – 6 mm、3 – 9 mm、11 – 17 mm和16 – 22 mm．对该姿态下灭弧室零件姿态调整，需用到夹爪3和夹爪4．

灭弧室夹取和调整方法示意图如图4（a）所示，需要经过4个变换过程．首先将灭弧室从1状态绕Z轴旋转一定角度调整为2状态，然后绕Y轴顺时针旋转90度以3状态放入灭弧室调整机构中，最后使用夹爪4将灭弧室调整为4状态放入零件托盘中．图4（b）为其他零件某种姿态调整示意图，包括磁轭、大U、磁组件和手柄，可以按照类似于图4（a）中灭弧室的方法进行姿态调整，并最终以指定姿态将不同零件放置于零件托盘（图5），并进行最终装配．

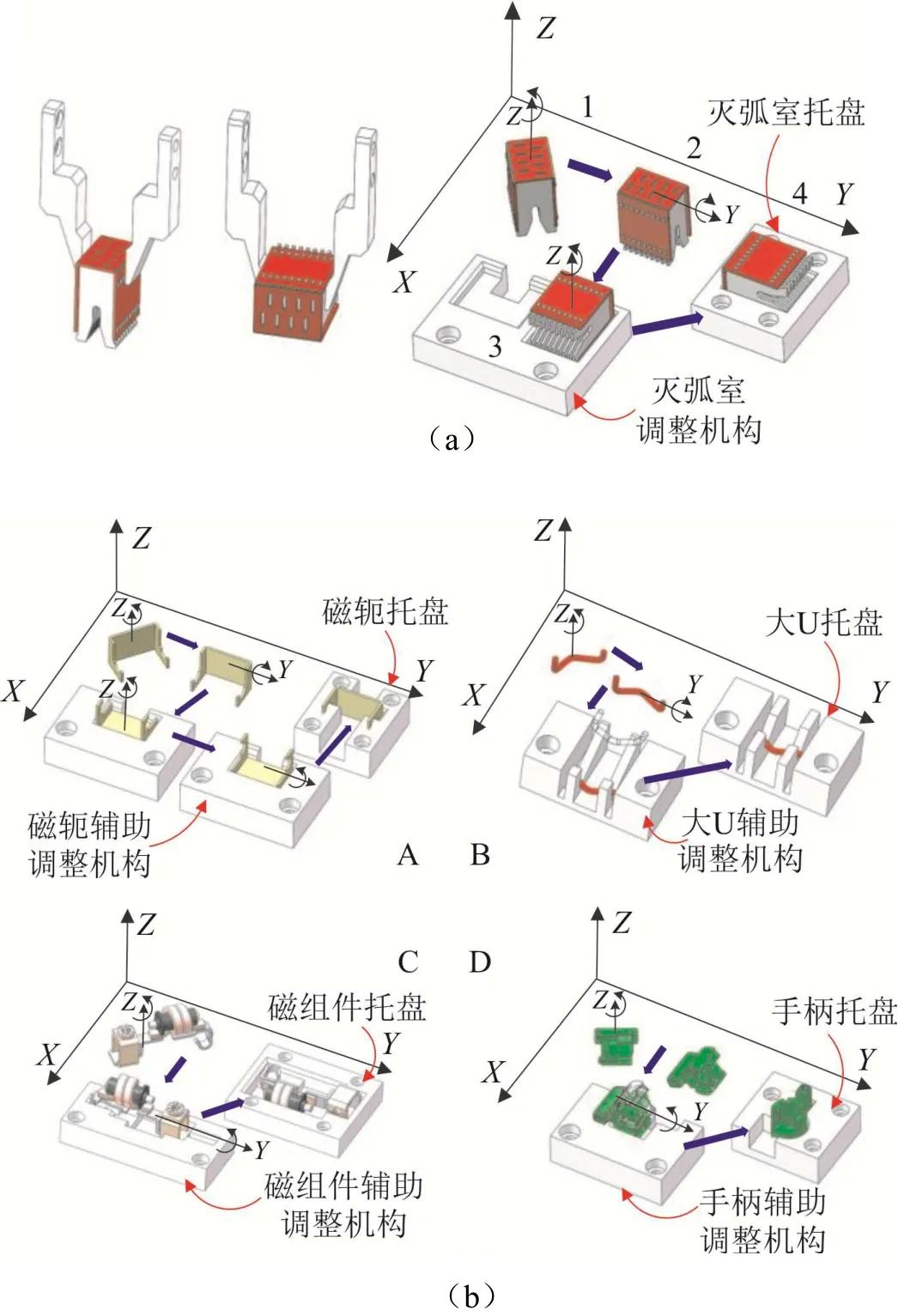
图4 不同断路器零件的柔性装配过程

1.2 机器人运动学分析

图6所示为六轴机器人模型及其连杆坐标系，根据D-H法[13-14]建立机器人相邻关节空间的数学模型，C4机器人D-H参数如表1所示．

D-H建模方法是由Denavit和Hartenberg[15]提出的，主要用于机器人运动学分析，通过齐次坐标变换来实现两个连杆上坐标的变换．由D-H法确定两相邻连杆之间的坐标变换通式为：

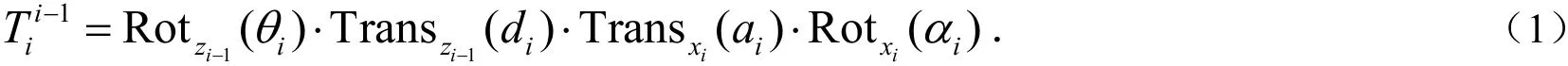
对任一关节连杆i，θ为关节角变量，d是沿关节i轴线的两个公垂线的距离，a为两个关节轴线沿公垂线的距离，即连杆长度，α是在垂直a的平面内两个轴线的夹角，即连杆扭角．

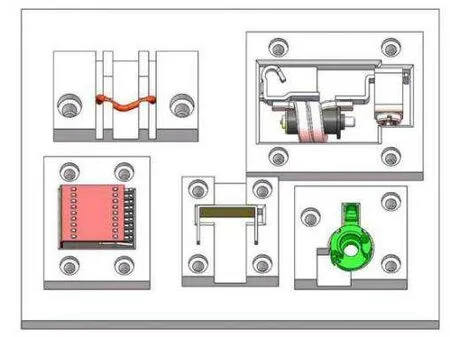
图5 不同零件以指定姿态放置

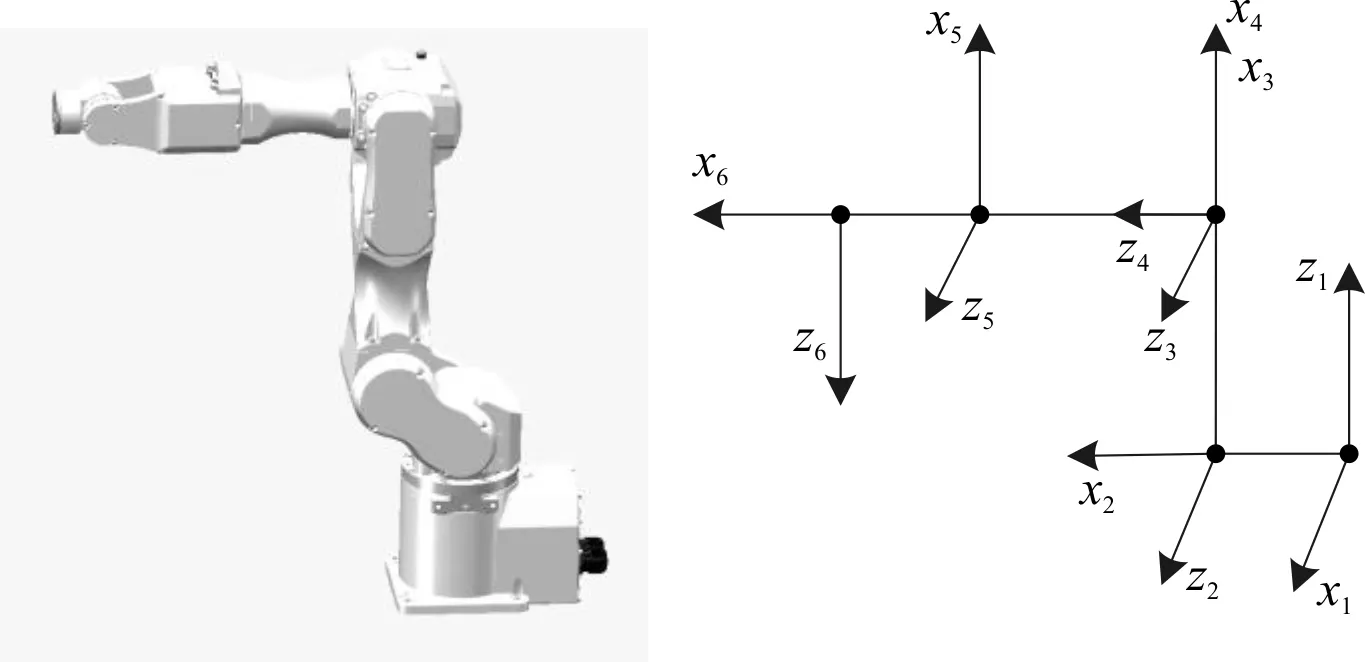
图6 柔性装配机器人模型与连杆坐标系

表1 六轴机器人D-H参数

本文在关节空间进行轨迹规划，所以对机器人进行运动学分析时，需要研究机器人末端执行器和基坐标系的对应关系．由上述坐标变换通式（1）可得机器人末端执行器到基坐标系的齐次变换矩阵为：

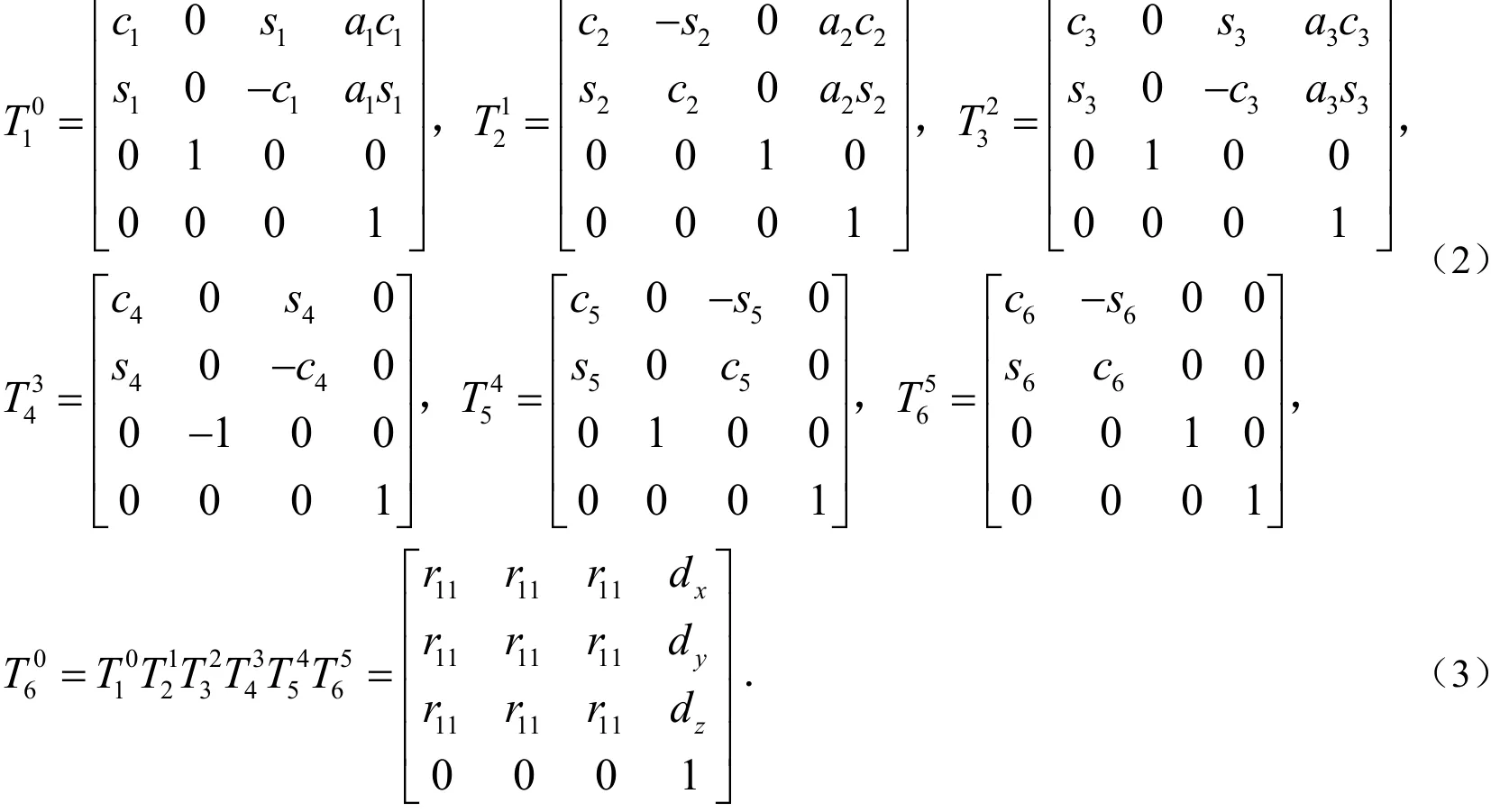
1.3 三次样条轨迹规划

轨迹规划是根据机器人作业任务要求，确定机器人各关节角度、角速度和角加速度关于时间的函数．对于断路器零件柔性装配任务，机械臂虽然在笛卡尔空间内不需要严格要求运动轨迹，但由于工作台面复杂，不仅需要规定机械臂的起始点，还要指明两点之间的若干中间点，如避障点、离开点、接近点等，需要沿经过这些点的特定路径运动．样条插值是一种常用的平滑曲线插值方法，本文采用三次样条来完成机器人在关节空间中的轨迹规划．

三次样条插值实质上是在机械臂运动过程中每段轨迹运动时间确定的情况下，求解样条函数的系数，再求导得到机器人速度和加速度对时间t变化的函数，从而确定机器人对时间t的运动情况．样条曲线θ(t)是一个分段定义的函数，其插值函数如（4）式所示，

其中，θi(t)是时间t的三次函数，其形式如（5）式所示，

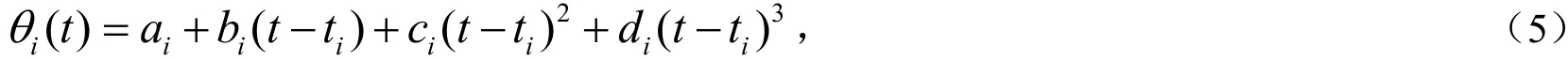
其中，ai,bi,ci,di为多项式的未知系数．

由已知条件和需要满足的约束，可求任意n+1个点的样条函数的系数．已知条件为：1）n+1个数据点表示机器人时间序列的关节值；2）每一分段函数都是三次多项式；3）节点处为二阶连续；4）起始端点速度为零．具体求解过程如下．

i）由曲线本身的微分式插值及微分的连续性以及样条可得：

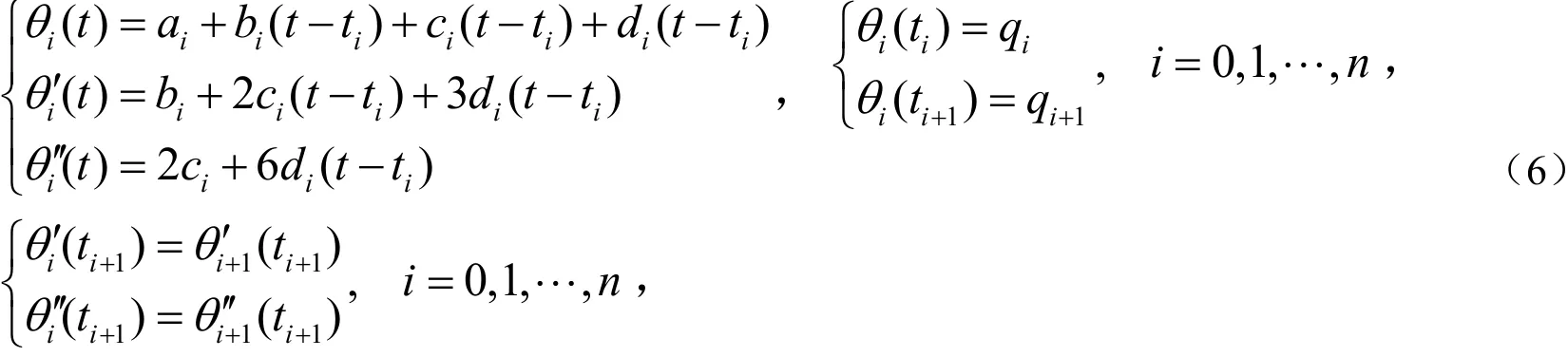
其中，iq表示机器人关节角度位置．

ii）将时间间隔hi=ti+1-ti带入样条曲线的条件，即（6）式中，可得多项式系数表达式：

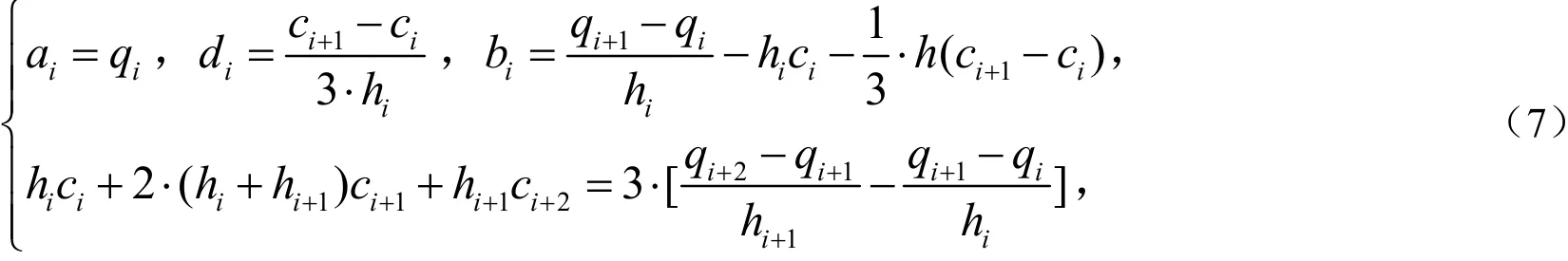
其中，a为每段初始时的机器人关节角度，系数c可由已知点和时间间隔求得，系数b,d可由c表示，所以求出系数c即可求得所有系数．

iii）由（7）式中i的取值范围可知，共有n-1个公式，还需要另外的约束条件，根据实际情况对起始点的速度加以限制，机器人起点和终点速度为零，结合（7）式中关于c的方程，可得：

其中，

从而最终获得样条函数的各项系数，对机器人的运动轨迹进行描述．

2 柔性机器人最优轨迹规划

2.1 粒子群优化算法

断路器柔性化装配过程中，需要对机器人运动性能进行优化，在保证机器人速度平滑，加速度连续有界的情况下尽可能减小运动时间．通过三次样条插值分析机器人运动轨迹后，需要对轨迹运动时间进行评判，以寻找到机器人从开始运动、经过中间节点、到停止运动的最小时间．

粒子群算法[16-17]（Particle Swarm Optimization，简称PSO）是一种模拟鸟群觅食行为的方法，属于进化算法的一种．PSO由随机解开始，通过迭代找寻最优解．在一个N维目标搜索空间中，有M个粒子组成一个群落，每个粒子及其速度都是一个N维向量．通过定义的适应度函数来确定粒子所找到解的优劣，在每次迭代中粒子通过两个极值进行更新，一个是粒子本身每次迭代的最优解，该解称为个体极值，另一个是整个种群当前找到的最优解，该解是群体极值．粒子群根据搜索到的最优值与过去搜索到的最优值进行比对，从而确定全局最优解．

PSO算法的更新公式为：

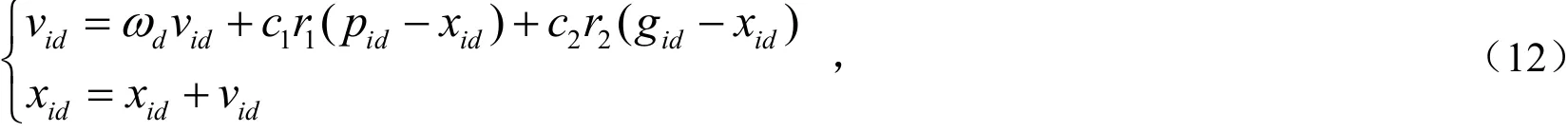
其中，ω为惯性权重，本文ω取值根据（10）式进行实时更新；1c,c2为学习因子，本文1c,c2取值为1.96；1r,2r是[0,1]内的随机数．当1c为零c2不为零时，粒子失去自我认知能力，只具有社会学习能力，此模型被称作全局PSO算法；当1c不为零c2为零时，粒子失去获取社会信息的能力，只有本身信息的认知模型，此模型则为局部PSO算法．

在（12）式中，每个粒子速度更新取决于三部分，分别是：粒子保持本身过去速度趋势的wdvid因子；粒子根据过去经验调整自身速度向粒子历史最佳的方向逼近的因子；粒子根据群体共享信息向群体最佳方向靠拢趋势的因子．（13）式中的Maxgen为最大迭代次数，本文最大迭代次数为15，d为当前迭代次数，ωmax设为0.9，ωmin设为0.4．

本文通过粒子群算法对机器人运动时间进行优化，优化的适应度函数为每个关节总运动时间：

根据三次样条轨迹规划方法，求得表示机器人关于时间的运动轨迹多项式，通过下面（15）式中机器人运动速度和加速度的约束条件判断运动轨迹的范围，从而确定粒子找到时间解的合理性，再与目标函数进行对比来判断每代粒子最优解的优劣性．

式中jiθ表示第j关节第i段多项式函数的值．

2.2 双重寻优PSO轨迹优化

使用粒子群算法对机器人轨迹进行优化时，每次迭代均需判断粒子群中个体粒子时间解的合理性．对轨迹时间进行优化时，其适应度函数为轨迹不同分段时间的和，通过比对该值来确定解的优劣性．而粒子每一维的数值是随机的，导致得到的适应度数值也是随机的，算法寻找最优解的能力不强．本文提出双重寻优的轨迹规划新方法，在判断适应度函数解的优劣性的基础上，再次判断粒子中每一分段轨迹所对应的时间极值，进行二次寻优，进而提高轨迹规划的可靠性与准确性．实现改进粒子群轨迹优化方法主要有4个步骤，其流程如图7所示．具体步骤如下．

1）粒子群参数初始化，包括种群数量M，迭代次数Maxgen，参数ω,1c,c2，机器人运动中间节点，粒子时间及其速度的随机解等，其中最重要的是给出随机的粒子群，粒子群中粒子参数包括各分段轨迹的运动时间和用于更新该时间的粒子速度．粒子群的时间解需根据粒子可能需要的运动时间范围进行随机确定．

2）根据上一步得到的随机粒子计算对应每个粒子时间解的轨迹，该轨迹是机器人关节、关节速度和关节加速度的函数．通过机器人速度和加速度约束判断每个粒子对应轨迹的合理性，并根据适应度值判断符合要求的粒子所对应时间的优劣性，以种群中所有粒子每一分段轨迹相加的最小值作为第一代群体极值，将群体极值最优的粒子通过G1表示，粒子的个体极值是每个粒子本身的解，通过H1表示．

3）进行算法第二次迭代，根据粒子群算法更新每个粒子的时间，再次由机器人速度加速度约束判断粒子时间的合理性，剔除不合理的解．然后，根据适应度函数更新粒子群的个体极值H1和群体极值G1．对于得到的每个粒子的个体极值，从算法第二次迭代开始，在判断粒子群时间解的合理性后，除了对每个粒子适应度值对比得到粒子的个体极值矩阵H1之外，还需要通过和上一代粒子中每一维时间值进行对比，得到潜在的更小的个体极值矩阵H2，判断新的矩阵H2对应时间解的合理性，若H2中有粒子满足要求，则将H2中合理的粒子替换掉H1中对应的粒子，并更新二次比对之后新的群体极值G1，否则H1和G1均不变．

4）进行下一步迭代，直至迭代次数结束．

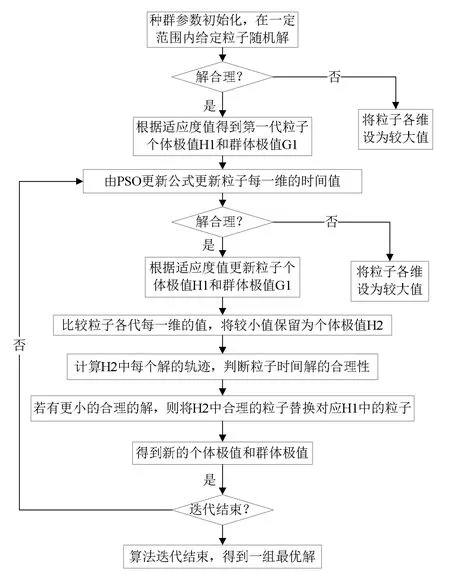
图7 双重寻优PSO轨迹优化流程图

2.3 仿真结果与分析

以断路器柔性化装配作业对算法进行验证，在图2所示的装配作业过程中，机器人需要借助相应的辅助机构完成作业任务，其运动过程包括4个分段（图8所示）：AB段表示机器人从安全点启动到取件坐标点夹取零件；BC段表示机器人夹取零件到变换姿态将零件放到调整机构上；CD段表示机器人松开零件并变换姿态后以另一种姿态夹取调整机构上的零件；DE段表示机器人从调整机构上夹取零件并放置到零件托盘．机器人作业过程中需要经过相应避障点，以避免机器人运动或位姿变换过程中与周围机构发生碰撞．以断路器磁系统的某一姿态为例进行说明，机器人调整过程中需要经过的节点各关节值如表2所示．

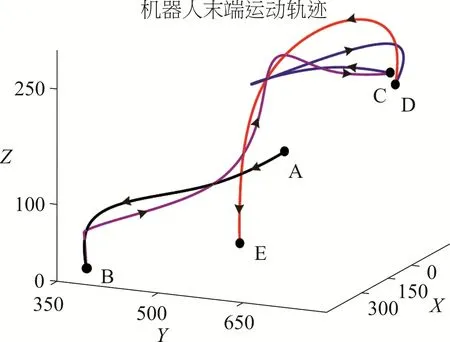
图8 柔性机器人分段作业路径示意图

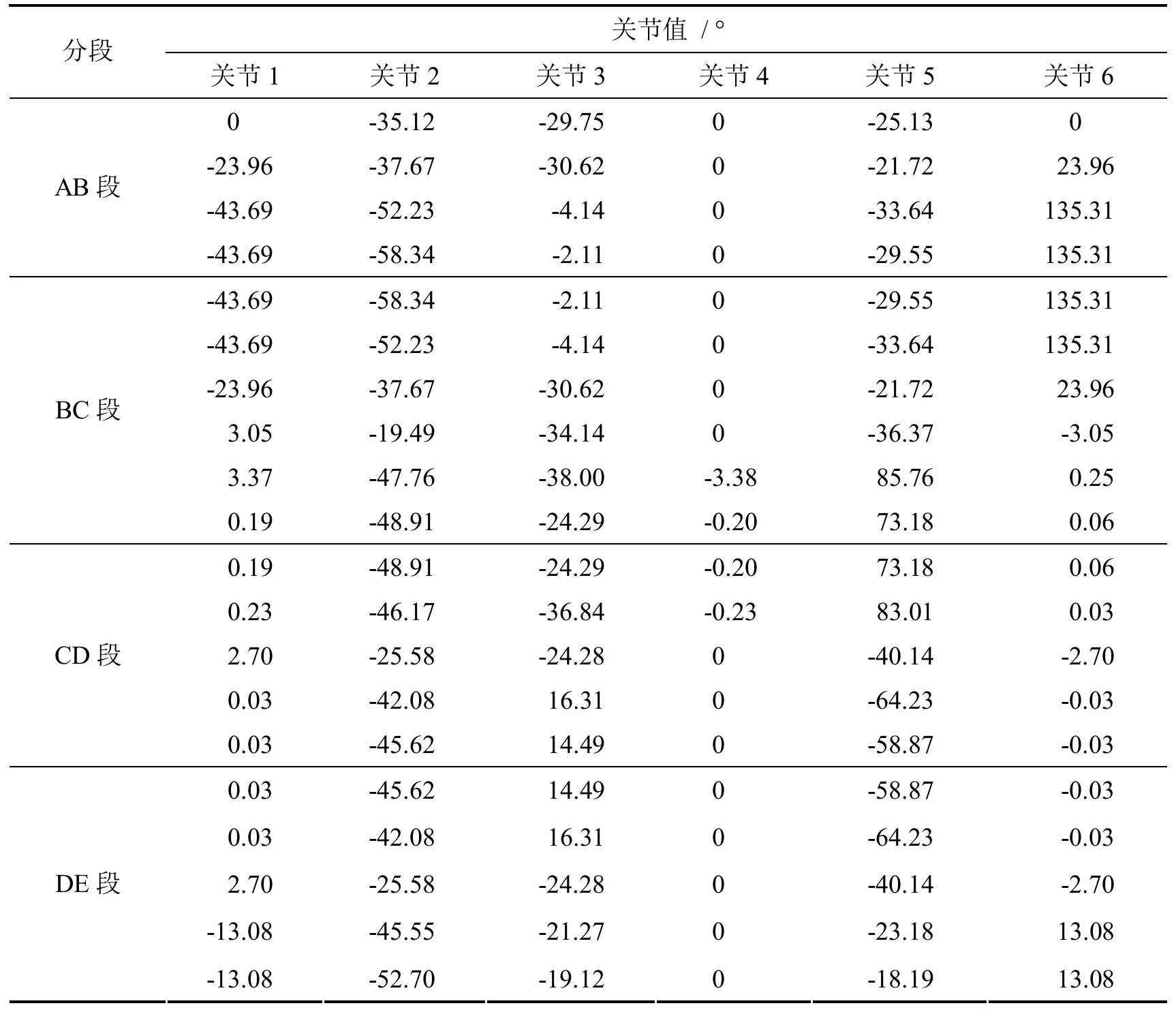
表2 机器人姿态调整运动节点及关节值

由表2可知，机器人在AB段经过4个点，BC段需要经过6个点，CD段和DE段各需要经过5个点．图8为各阶段机器人末端执行器在笛卡尔空间中的运动轨迹．机器人从初始A点运动到相机拍照区域的B点夹取零件，再从B点运动到C点处的调整机构放置零件，接着机器人调整末端执行器姿态到D点再次夹取零件，最终运动到E点完成零件姿态的调整任务．

对上述关节和各运动阶段分别进行优化．对于优化后每一阶段每一分段的时间，由于机器人从一个点运动到另一个点时各关节需要同时运动，所以取每一小段优化时间中最大值作为该段各关节的运动时间．由于关节4在AB段和DE段关节值完全没有变化，所以不考虑该关节在这两段轨迹时间的优化，此外，对其他关节点没有变化的分段，其两点之间的运动时间采用其他关节优化结果中的最大时间．

为进行对比，本文优化前时间设置为机器人可能的运动时间范围内的随机值．优化前后得到的各分段最大运动时间如表3所示，由该表可以看出，改进前后的算法在每一分段轨迹的所需最大运动时间结果上存在以下差异：改进前的优化结果可能出现各段时间极度不均衡的情况，而改进后的算法基本遵循运动关节所需运动角度越长则时间越长的规则，说明改进后算法得到的优化结果更加合理．此外，相比于优化前所取的随机值，改进后的时间结果都有所减小．同时，将表中机器人每个运动阶段总的时间进行对比，相比随机设置的运动时间，未进行改进的优化算法在AB段、BC段、CD段、DE段分别缩短了11.9%、22%、22.6%、9.9%．优化算法进行双重寻优以后，各分段分别缩短了37.9%、25.6%、39.5%、17.3%．由该结果可以看出，进行双重寻优改进后的算法相比改进前的算法成效更优，分别提高了26%、3.6%、16.9%和7.4%．

图9为使用改进后的粒子群算法对机器人每个阶段运动时间进行优化前后的各关节运动轨迹．由该图可以看出，优化后轨迹较优化前轨迹运行时间明显缩短，速度和加速度也更接近允许的最大值．

3 实验平台搭建与验证

图10为机器人运动程序执行的总体流程图．在程序开始执行后，机器人在电机控制下首先运动到安全的起始点位置，与此同时机器人末端执行器上各夹爪回到初始位置．然后，通过以太网和相机建立连接，连接成功后向相机发送请求零件信息命令，所需信息包含零件的种类、姿态和坐标等．若此时相机区域检测有零件，则相机拍照后发送零件信息给机器人，机器人以一定时间间隔读取相机对应端口信息．机器人接到相应信息后，对该信息进行处理，以判断零件的种类和姿态信息，再根据轨迹规划结果执行对应姿态情况下机器人的运动程序，完成相应姿态下零件柔性装配任务．机器人运动执行完成后，返回初始位置并请求和等待相机下一次发送的信息指令．

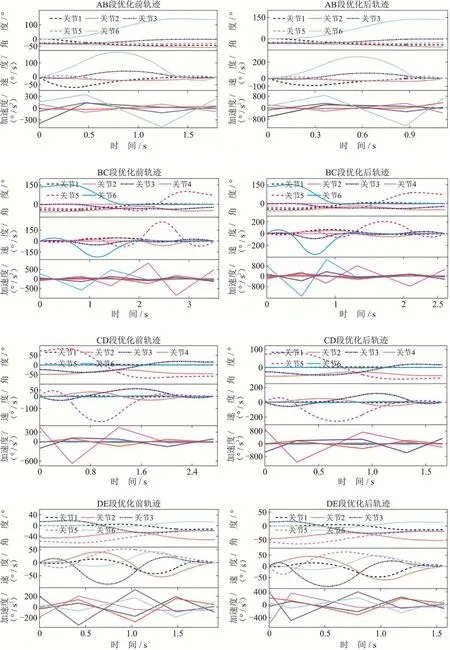
图9 优化前后轨迹图

断路器柔性装配系统中的姿态调整单元实验平台如图11所示，主要包括六轴机器人、末端执行机构、姿态调整辅助机构和托盘机构等．

图12所示为两次实验验证及其结果，两次实验中零件为随机初始位姿，机器人夹取零件并经姿态辅助机构调整后将零件以目标姿态放到托盘中．实验结果表明，针对图1所示的5种零件及其随机姿态，柔性机器人均可以成功实现零件的柔性化姿态调整和装配作业．

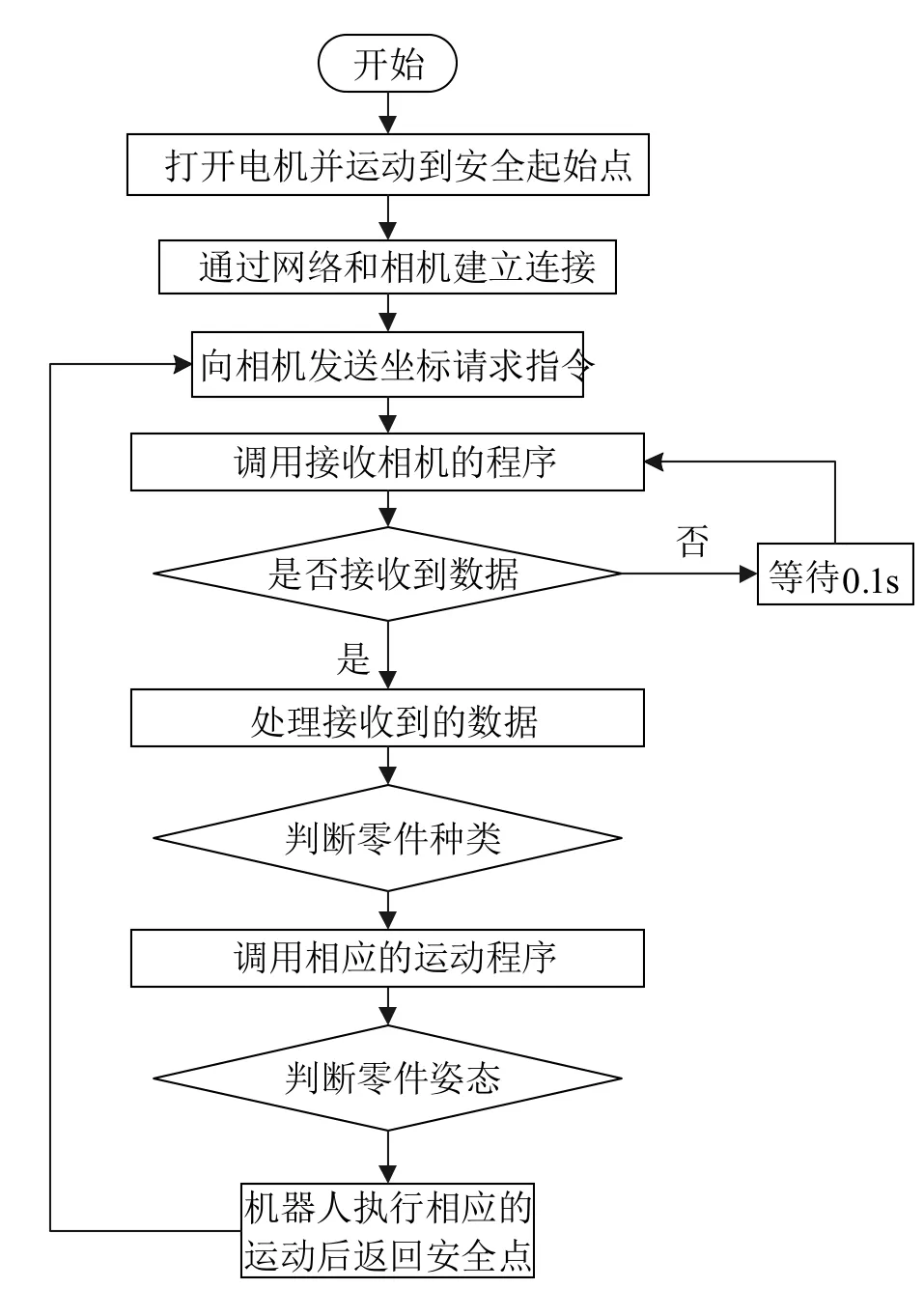
图10 程序总流程图

图11 姿态调整单元实验平台

图12 实验验证结果

4 结 论

本文提出一种双重寻优的机器人轨迹规划新方法，分别比对机器人每一分段轨迹对应的分段时间并进行二次寻优，得到在运动速度和加速度约束条件下的整体潜在更优解，执行效率上分别提高了26%、3.6%、16.9% 和7.4%．在此优化结果的基础上，提出了一种断路器柔性装配新方法，可以实现不同零件在随机姿态下的柔性化调整完成装配任务．结合六轴机器人平台对方案进行了实验验证，结果证明了所设计方案的可行性和合理性．