不锈钢小径管跑道型脉冲涡流测厚传感器研究*

宋 韵， 武新军

(华中科技大学 机械科学与工程学院，湖北 武汉430074)

0 引 言

不锈钢管广泛应用于石油、化工、电力等行业。在长期服役中，管道内壁容易发生流动加速腐蚀[1]，特别是在一些小直径的连接管道中，由于流量快速变化，更容易发生侵蚀和腐蚀。然而，在复杂现场环境中，无损检测传感器的布置可能会受到限制。脉冲涡流检测(pulsed eddy current testing,PECT)技术可以实现在传感器一定提离的情况下，检测管道内壁的腐蚀情况，在工业工程中得到广泛应用[2]。

目前，PECT的研究主要集中在大直径的管道上，管道可以近似为平板，相应的理论模型和传感器设计研究相对成熟[3,4]。各种传感器结构也被应用于不同检测对象和场景。如矩形激励线圈[5]可在试件中激励出更均匀的涡流，对缺陷更加敏感；圆台型激励线圈[6]相对于圆柱型线圈，对腐蚀性缺陷有更高灵敏度。对于小直径管道，PECT目前仅被用于铁磁性管道的检测中[7]。

本文研究非铁磁性材料小径管的PECT问题，提出一种由跑道型激励线圈和同形状接收线圈组成的传感器，其特点是改变电磁辐射的方向，将电磁能量集中在管道区域。通过改变传感器结构提升管道上的有效电磁辐射分布范围，提高传感器对小径管壁厚的分辨力。

1 小径管脉冲涡流测厚原理

圆柱型线圈检测平板或可以近似为平板的大直径管道时，由线圈激励出的动态磁场在试件中感应出的涡流呈圆形分布，如图1(a)所示。由于涡流在试件中远离圆柱线圈轴线的位置迅速减小，甚至在板的边缘处可以忽略不计。因此，只有中心区域的涡流场对检测有用，该区域可称为传感器在构件上的有效覆盖区域[8]。

然而，当圆柱型线圈用于非铁磁性管道检测时，由于它不像铁磁材料那样具有磁聚焦特性[9]。当管道外径较小，与激励线圈的尺寸接近时，电磁能量不能集中在管道区域，因此会发生大量的耗散，有效覆盖区域的形状会变成一个三维空间曲面上的椭圆而不再是圆，如图1(b)所示。其中椭圆的长轴与线圈的外径相关，而与短轴则取决于管道的直径。具体来说，管道的外径越小，椭圆形有效覆盖区域的短轴越短。同时，沿着管道周向远离线圈轴心，提离也会随着增大，这也会进一步缩小激励线圈的有效覆盖区域。因此可以推测，相同的圆柱型线圈在平板上的有效覆盖区域远大于其在小径管上的覆盖区域。

图1 电磁能量分布示意

考虑到小径管结构，有效覆盖区域的面积受管道尺寸限制。因此，本文提出一种如图2(a)所示的跑道形状激励线圈结构，可以延长椭圆形有效覆盖区域的长轴。可以预见，若保持跑道型线圈的体积不变，随着直道长度L增加，激励能量在管道上有效覆盖区域面积很可能会增加，并在L增加到一定程度时，中心最大涡流密度会有所减小。因此，合适尺寸的跑道型线圈可以在中心涡流密度不产生大幅降低的情况下，有效扩大其在管道上的有效覆盖区域。

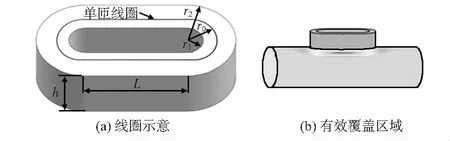
图2 跑道型线圈检测管道

2 跑道型传感器解析模型

为研究跑道型传感器对非铁磁性小径管的检测性能，建立其理论模型开展PECT测厚性能研究。由于三维脉冲涡流场的有限元模型复杂度高，计算耗时长，本文基于跑道型传感器的解析模型对检测信号进行分析。

2.1 解析计算及验证

首先根据已有的圆柱型线圈管道瞬态解析解[10]，PECT的感应电压信号表达式见式(1)

(1)

式中Γ为与管道相关的系数，其表达式与管道电磁参数和几何参数有关，可通过管道和空气内外边界处的边界条件解出，具体表达式见文献[10]；Csmd和Csmp分别为与激励线圈和接收线圈有关的系数，满足表达式(2)

(2)

式中r1和r2分别为图2(a)跑道型线圈弯道部分的内半径和外半径，h为线圈高度，lo为线圈下端面距离管道上表面的提离距离，D为被测管道外径；r0和l分别为单圈线圈的弯道半径和其距离管道上表面的距离，Cssm为单匝线圈的线圈系数，其表达式见式(3)

(3)

式中SQ为线圈所围成的面积。

在笛卡尔坐标系下，式(3)可简化为式(4)

(4)

式中L为图2(a)中的线圈直道长度。

将式(4)的求解结果代入式(2)，求解得到跑道型线圈的线圈系数Csmd和Csmp，并进一步代入式(1)的感应电压信号表达式中，可得到跑道型线圈的PECT检测信号。

用MATLAB编程实现式(1)中感应电压信号。将计算结果与三维有限元仿真结果进行比较，验证解析计算的正确性。其中解析计算采用MATLAB R2017a进行，有限元计算结果采用ANSYS Electronics17.2进行计算。解析计算和有限元计算中使用的传感器和管道的参数均保持一致，跑道型传感器的激励线圈和接收线圈参数见表1，被测管道为外径100 mm，壁厚10 mm的不锈钢管，其相对磁导率为1，电导率为1.35×106S/m。

表1 跑道型传感器的参数

解析和有限元计算结果如图3所示。

图3 解析计算结果与有限元结果对比

从图3中可以看出，解析计算结果与有限元仿真结果得到的信号衰减规律基本一致。采用残差平方和(residual sum of squares,RSS)来量化两者计算得到的感应电压偏差，其表达式为

RSS=∑(ΔU-ΔUFEM)2

(5)

式中 ΔU为解析计算的感应电压，ΔUFEM为有限元计算的感应电压。计算得到RSS为0.029 5，这说明解析计算结果是可信的。因此，可以使用该解析模型预测跑道型传感器的脉冲涡流检测信号，并进行信号特性分析。

2.2 基于解析模型的测厚性能研究

基于解析模型对PECT传感器对小径管测厚能力进行研究。使用解析模型计算外径89.0 mm的不锈钢管的检测信号，管道壁厚分别设为6.7，7.8，8.9，10.0，11.1 mm。假想壁厚11.1 mm的不锈钢管为无壁厚减薄的情况，而其他壁厚模拟管道发生不同程度壁厚减薄的情况。跑道型传感器的参数继续使用表1中的参数，同时，引入体积相同的圆柱激励线圈作为对比，线圈参数：内半径r1为3.5 mm，外半径r2为29 mm，高度h为26 mm，匝数N为600。其电阻值与表1中的跑道型激励线圈相同，接收线圈保持一致。

解析计算得到的不同壁厚不锈钢管的PECT信号如图4所示。

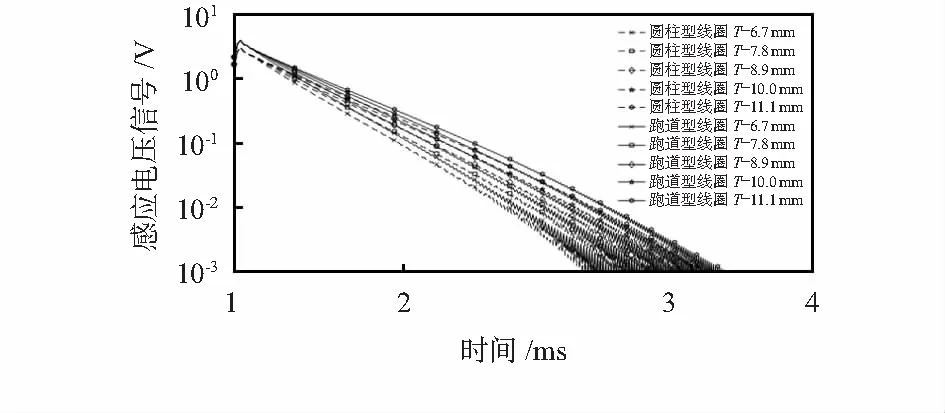
图4 不同壁厚不锈钢管的PECT解析计算信号

图4中，实线表示跑道型激励线圈的PECT信号，而虚线则是作为对比的圆柱型激励线圈的信号。由图可以看出，在检测不同壁厚管道时，跑道型激励线圈信号幅值始终大于圆柱型激励线圈，有利于信号采集。然而PECT测厚时，有无壁厚减薄信号之间的差异性是测厚中更为关心的，信号的差异性难以从图中直观地看出，选用式(6)中的欧氏距离来量化

(6)

式中 ΔU为壁厚减薄管道感应电压信号，ΔUref为无壁厚减薄管道的标准感应电压信号。对于跑道型传感器，计算得到不同程度壁厚减薄的检测信号与无壁厚减薄的标准信号之间的欧氏距离见图5。

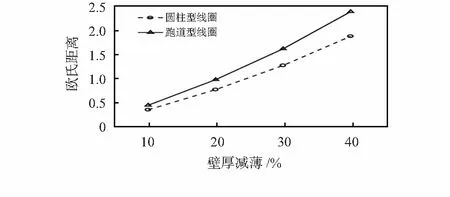
图5 两种线圈测厚能力的实验对比

由图5可以看出，不管是使用跑道型还是圆柱型传感器，壁厚减薄信号相对标准信号的欧氏距离与管道壁厚减薄百分比呈正相关。而使用跑道型激励线圈时信号间的欧氏距离大于使用圆柱型激励线圈时的，因此跑道型激励线圈对不锈钢小径管的壁厚变化更为灵敏。

3 实验验证

为验证上述基于解析模型的测厚性能分析，制作如图6 所示的304不锈钢阶梯管试件，阶梯管分为5段，每段长度为200 mm，外径分别为89.0，86.8，84.6，82.4，80.2 mm，管壁厚度对应分别为11.1，10.0，8.9，7.8，6.7 mm。

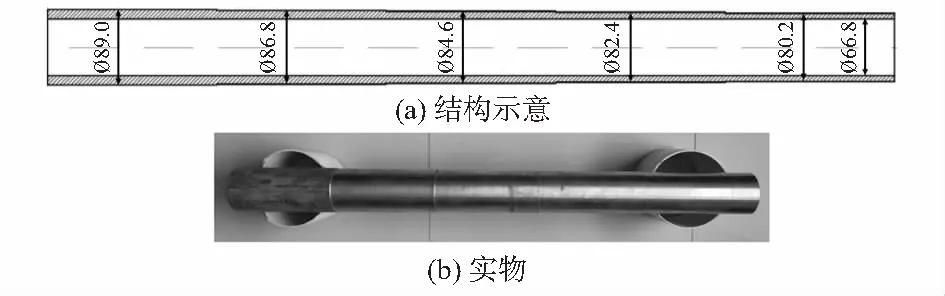
图6 待测阶梯管

实验中采用与解析计算相同的圆柱型和跑道型传感器，激励线圈的体积保持一致，并使用统一的接收线圈，分别测量2只传感器位于阶梯管不同位置时接收线圈内的感应电压信号，结果如图7所示。

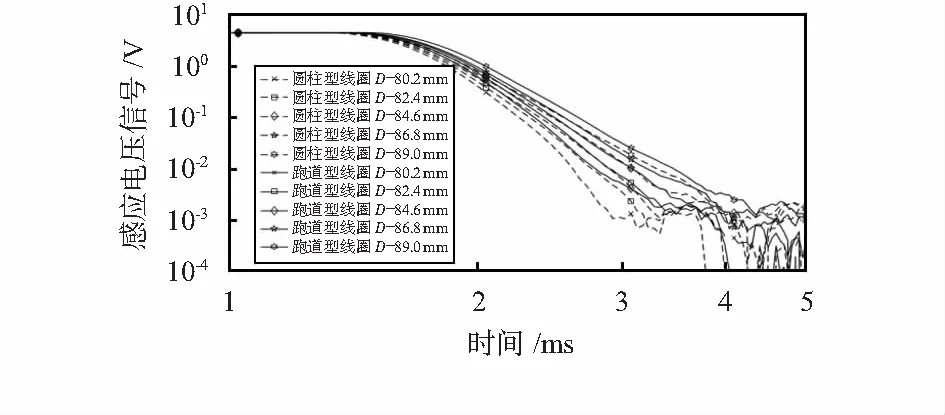
图7 全部实验信号

与解析计算的结果一致，跑道型激励线圈的信号幅值更大。同样用欧氏距离量化壁厚减薄信号与标准信号的差异，图8为欧氏距离与相对壁厚减薄的关系图。图8可以验证解析计算的分析，跑道型传感器的测厚能力高于圆柱型。

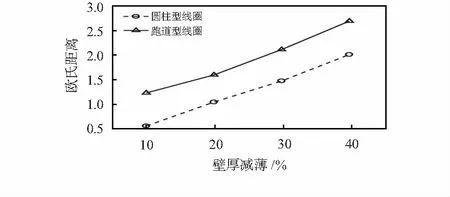
图8 两种线圈测厚能力的实验对比

4 结 论

本文针对电磁能量不能集中在小直径非铁磁管上，从而耗散大量能量的问题，提出跑道型激励线圈的PECT传感器，该传感器可以改变电磁波辐射覆盖区域形状，从而将电磁能量集中在管道上。首先，分析了两种类型传感器在小径管上的有效覆盖区域，圆柱型激励线圈在管道上的覆盖区域非常有限，跑道型激励线圈则有效地扩大了管道的覆盖范围。其次，基于解析模型研究了两种激励线圈的PECT信号特性，与圆柱型激励线圈相比，跑道型激励线圈的信号幅值更高，衰减更慢，且测厚性能更优。最后，在阶梯管上进行了实验验证，实验结果与解析模型的结论一致：跑道型传感器在不锈钢小径管的壁厚分辨力上具有明显的优势。