基于PCB罗氏线圈的反窃电在线监测系统设计*

杨 鑫, 张家洪, 沈 鑫, 鲍 毅, 李英娜, 李 川

(1.昆明理工大学 信息工程与自动化学院,云南 昆明 650500；2.昆明理工大学 机电工程学院,云南 昆明 650500)

0 引 言

智能电网的建设离不开对坚实可靠配电网的建设。反窃电监测离不开对配电网的电流监测,而配电网电流监测数据的可靠性主要取决于电流传感器的可靠性[1～4]。目前,CT[5]、霍尔元件[6]、罗氏线圈[4]以及光纤电流互感器[7]等都是被广泛投入使用的电流测量装置。传统的电磁式电流互感器由于会存在铁磁饱和而导致波形严重畸变等问题,已经无法能满足电力系统发展需求[5]。配电网线路量大、面积广、线路长,需要低成本、易带电安装的检测装置。霍尔元件传感器的测量精度受环境的影响较大,缺乏稳定性[6]。光纤电流传感器成本高、结构复杂,不利于实际使用[7]。而罗氏线圈因其具有测量时快速响应以及测量精度高等优点,将会在现阶段的电力测量领域中占据愈发重要的地位。但常规的罗氏线圈因价格昂贵而难以被大规模使用,且测量电流时的性能表现受制造精细度的影响[8]。而PCB罗氏线圈除拥有普通罗氏线圈的优良特性外,还具有制造成本低、容易大规模量产等特点,其目前已经在电力测量中得到了应用[9～12]。反制窃电对提升用电安全及供电可靠性有着重要的意义,对配电网的电流监测将有助于打击用户的窃电行为,文献[13]针对低压侧用户的线损问题,设计了一整套的远程监控、数据收集和分析系统,实时监测系统将有助于电力企业打击用户窃电行为。

本文设计了一种基于PCB罗氏线圈的反窃电在线监测系统,仿真分析表明该系统能够解决反窃电中的准确性、快速性及有效性问题。

1 反窃电在线监测系统

所设计的系统主要分为三部分组成,分别是电流采集模块、通信与信号处理模块和远端服务器。图1为该系统的整体框图[14]。

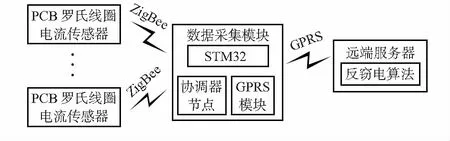
图1 系统整体框图

2 PCB罗氏线圈设计

2.1 罗氏线圈结构参数分析

PCB罗氏线圈结构示意图如图2所示。图中矩形框表示罗氏线圈的骨架,S为其横截面积,h为矩形骨架的长,d为骨架的宽,D为线圈的中心半径。

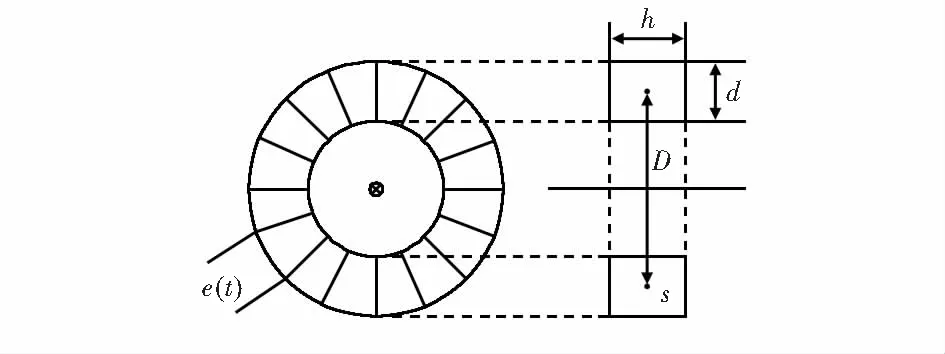
图2 矩形罗氏线圈结构示意

忽略线圈的分布电容,经过推导可以得到线圈传递函数的一种变形形式为

(1)

式中n为线圈匝数,Rs为线圈的采样电阻,式(1)中α=rt+Rs/NM,N=n/2πR,其中，R为被测载流导体至线圈的中心半径,M为线圈与载流导体间的互感

(2)

(3)

式中ρ为铜导线的电阻率系数且取ρ=0.018 51 Ω·mm2/m,μ为真空环境中的磁导率系数且取μ=4 π×10-7H/m。

2.2 线圈结构参数对其动态特性的影响

如图3所示为不同匝数、径向和轴向长度下矩形罗氏线圈的阶跃响应曲线图,矩形罗氏线圈的参数D=60 mm,Rs=150 Ω。

图3 不同参数下罗氏线圈的阶跃响应曲线

图3(a)中取d=10 mm,h=1.8 mm,分别取n=600，n=800和n=1 000,由图3(a)可知,随着匝数n的增大,矩形罗氏线圈阶跃响应到达稳定的速率减慢。图3(b)中取n=1 000,d分别取10,20,30 mm，由图3(b)可知,矩形罗氏线圈的径向长度d越小,其阶跃响应所需时间越短,系统能越快达到稳定状态。图3(c)中取d=10 mm,n=1 000,h分别取1,2,3 mm，由图3(c)可知,矩形罗氏线圈的轴向长度h越小,其阶跃响应所需的时间就越短,系统能越快达到稳定状态。通过上述分析可知,线圈匝数n，径向长度d以及轴向长度h三个因素对矩形罗氏线圈动态特性的影响基本相同,这三个因素中任意一个增大,线圈的阶跃响应所需时间都会变长,即其达到稳定状态所需的时间变长。因此,在对罗氏线圈的结构参数进行选择时,应综合考虑实际测量的需求。

根据上述的分析结果,设计了三种不同规格PCB式罗氏线圈,其中线圈1的参数为径向长度d1=15 mm，轴向长度h1=1.8 mm，匝数n1=792；线圈2的参数为径向长度d2=20 mm，轴向长度h2=1.8 mm，匝数n2=792；线圈3的参数为径向长度d3=20 mm，轴向长度h3=1.8 mm，匝数n3=396。

3 电流数据采集

电流监测的数据采集模块如图1所示。其中主控与ZigBee协调器间采用UART协议进行通信,获取采集到的输电线路上的电压值,需要进一步通过拟合的关系式才能将电压值转换为一次侧的电流值,并经过相应的比对处理后封装成数据包,再以USART方式将数据包发送给GPRS通信模块,最终由GPRS通信模块传输相应的数据。本文所设计的系统中该模块的主控处理器为STM32F103；ZigBee协调器口除负责组建与管理ZigBee网络外,还需负责接收电流传感器节点发送的数据,ZigBee协调器的具体型号为CC2530；GPRS无线模块负责将主控模块处理的数据上传至远端服务器,由远端服务器负责疑似窃电用户的筛选工作,所使用的GPRS模块型号为SIM800A。此外,系统运行时需要采用锂电池作为供电电源,负责对数据采集模块中的上述三部分进行供电,确保该模块的正常运行。

主控单元通过串口发送标准AT命令来控制ZigBee协调器运作。图4所示为测试实物图,其中包括PCB罗氏线圈、数据采集模块、电流采集测试系统。

图4 系统测试实物

实验测试时使用220 V交流电源、调压器以及功率电阻,通过调节调压器和功率电阻值大小的方式来产生不同大小的电流,使载流导线穿过PCB罗氏线圈电流传感器,以获得感应输出。测试时电流从1.5 A变至8.5 A,系统采集电压并进行保存。受限于实验室条件,无法测试更大电流条件下的系统输出电压。将测试得到的3组数据进行线性拟合后得到如图5所示的曲线。

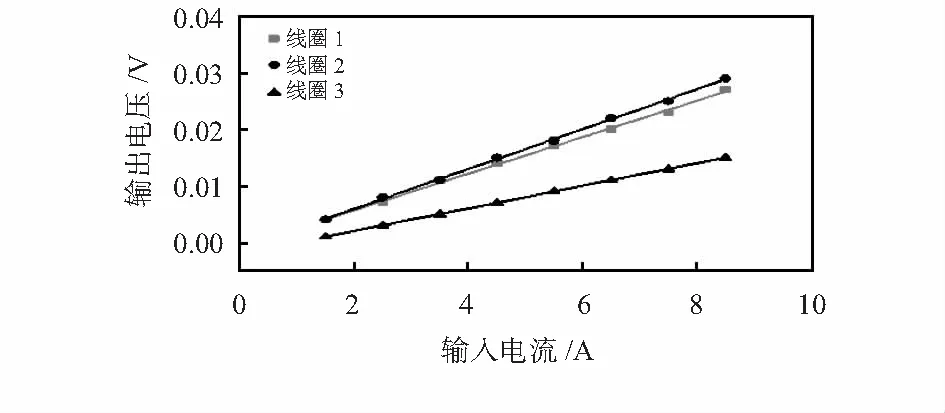
图5 三组线圈的输出拟合曲线

由图5可知,线圈1，线圈2和线圈3的灵敏度分别为3.23，3.52,2.0 mV/A,即径向长度越大,传感器实际测量时的灵敏度就越高；通过比较线圈2和线圈3可知,越多匝数的线圈其输出的电压信号值也越大；其最终的实测结果与仿真结果一致,三条曲线的R2分别为0.998 34,0.999 09和1。三条拟合曲线分别为y1=0.003 23x1+0.000 461,y2=0.003 52x2-0.000 881和y3=0.002x3-0.002。

4 算法仿真

针对分压和分流的窃电方式设计了采集高压端电流数据、同时读取低压侧电表电流数据并计算其比值作为研究值,采用离群点算法对用户三相高低压侧电流比值进行分析计算,找出离群点也即嫌疑窃电用户的方法。

基于距离的离群点算法的描述方式为DB(pct,dmin),即在一个数据集T中,如果有一个数据点o距离至少pct部分的其他数据的距离大于dmin,则o为数据集T的一个离群点。其中,pct为分数阈值,dmin为距离阈值。而距离作为筛选离群点的重要因素,常用的度量方式是欧氏距离,通过将二维空间中两点的距离拓展到高维空间,假设xi，yi分别为两个n维对象,则其n维属性集分别表示为Vx(Vi1,Vi2，…,Vin),Vy(Vj1,Vj2，…,Vjn),xi，yi两点之间的欧氏距离应为

(4)

比较两个数据点之间的欧氏距离,距离越大表明数据点间的差异也越大。因此,考虑将用户的多维用电数据作为离群点算法的输入数据集,通过正常的用户历史数据推算可以得出算法的分数阈值和距离阈值,采用欧氏距离作为度量方式,通过计算筛选出用户用电数据中的离群点,即可将此离群点用户视为疑似窃电用户。

假设有某用电户的某时间段用电数据为xm,取该时间段之前的n-1组用电数据,组成一个m×n的数据矩阵。组成的矩阵如式(5)所示

(5)

在本算法中,将三相电流数据与电表测量数据的比值作为输入,每小时取2组数据,其比值的计算方式如下式(6)所示,其余两相的计算方式也同样如此。

IA=I1/Iins

(6)

式中I1为高压端电流,Iins为低压侧电流。

本文所设计的基于距离的离群点反窃电算法的基本计算步骤为：1)导入m×n维的电流数据并进行数据的预处理；2)设置算法的参数分数阈值pct以及距离阈值dmin；3)计算所有数据中第k个数据点与其他所有数据点间的欧氏距离,并统计欧氏距离大于dmin的数据所占的比率P；4)若比率P大于等于所设定的阈值pct,即可将该数据对应的用户标记为疑似窃电用户并输出,直至所有数据计算完毕。

表1所示为某10 kV专变用户的高压一次侧电流与变压后二次侧的电流数据的比值数据。

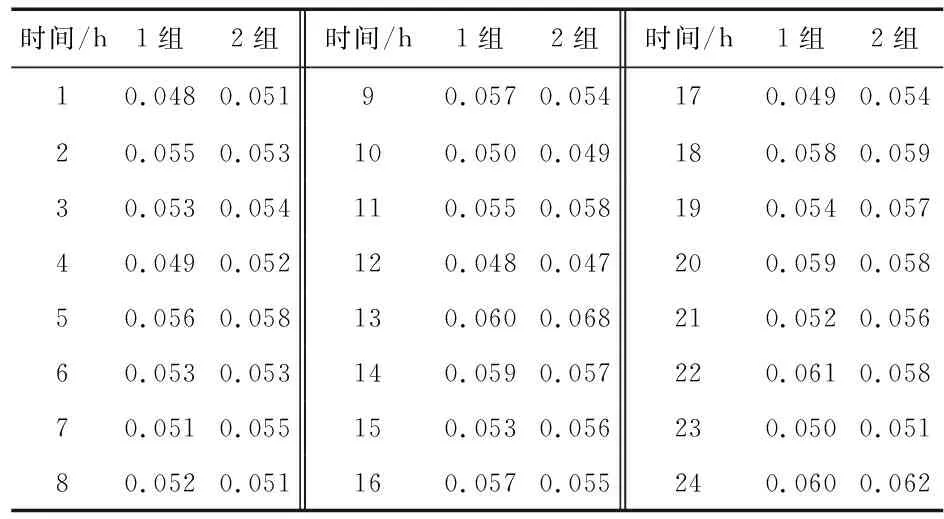
表1 某10 kV用户高压侧电流与低压侧电流比值

表1中每小时采集2组值,组成一个24×2维的矩阵,将该数据矩阵输入到所设计的离群点算法中,通过分析计算后将算法的分数阈值设置为0.8,欧氏距离阈值设置为0.01,进行仿真分析可以得到如图6所示的仿真结果。

图6 算法仿真结果

从图6可以看出,该离群点算法可以从数据集中筛选出与其他80 %数据的欧氏距离大于0.01的数据点。结合在线监测所获得的电流数据,该算法能够筛选出疑似窃电用户。

5 结 论

本文设计了一种基于PCB罗氏线圈的反窃电在线监测系统,其中高低压两侧间的数据传递通过ZigBee技术实现,检测数据则是由GPRS传输至远端服务器。设计了一种PCB罗氏线圈电流传感器,并对其结构及电磁参数进行仿真分析,最终制作了三种不同规格的PCB罗氏线圈电流传感器,灵敏度分别为3.23,3.52,2.0 mV/A。设计了一种基于距离的离群点反窃电算法,并对该算法的可行性进行了仿真分析,结果表明,采用该算法可实现一种反窃电在线监测系统,该系统具有一定的实用价值。