基于正负序列信号的提升机电机短路故障诊断*

冯文成, 王福忠

(河南理工大学 电气工程与自动化学院,河南 焦作 454000)

0 引 言

同步电动机可以避免传统的交流异步电动机存在的功率因数低、调速性能差等缺点,在大型矿用提升机得到了广泛应用。然而,如果同步电动机发生意外事故,将导致严重的经济损失。根据电力研究所(EPRI)和电机与电子工程师协会(IEEE)的电机故障报告,匝间短路故障(inter-turn short circuit fault,ISCF)是最常见的电机故障之一[1]。该故障不仅会产生很大的短路电流危害电机,还会引起其他类型的定子故障,如:相间短路、接地短路。因此,需要对ISCF进行诊断。

很多学者已经采用定子电流频谱分析法、基于模型分析法、基于数据分析法、基于信号分析法的方法对ISCF诊断进行了研究。其中,定子电流频谱分析法[2]是最传统的方法,这种方法虽然很简单,但是不能检测出ISCF的严重程度。基于数学模型分析的方法可以克服定子电流频谱分析法的缺点。然而,由于使用了数学模型,模型参数具有不确定性,准确的数学模型很难建立。基于数据的方法[3,4]使用人工智能工具,该方法对电机进行了快速、准确的仿真,但在正常运行和故障运行的情况下很难收集足够的数据。基于信号的方法使用各种信号,如电压、电流、转速以及旋转角度,其中包括Park的矢量方法[5]、定子电压空间矢量[6]和d-q轴信号分析[7]。根据诊断方法的种类,这种方法可以诊断出电机的严重程度。

为了诊断ISCF,近年来出现了很多基于信号的方法,这些方法仅使用电压和电流信号,例如:负序分量[8]和旋转角[9],不需要电机模型参数如定子电阻和电感,以及旋转角度。因此,这些现有的方法可以应用于提升机电机采用无传感器控制或电机参数不确定的情况。然而这些现有的方法用于诊断轻微的ISCF仍然存在困难,因为这种方法仅用到电压和电流信号的幅值或相位。为了克服这一缺点,本文提出了一种基于正负序列信号的故障诊断方法。该方法是利用电压和电流信号的幅值和相位来诊断ISCF。此外,在没有提升机电机模型参数和旋转角度的情况下,仅通过电压和电流信号就可以检测到轻微的ISCF。

本文分析了ISCF下正负序成分的特征,为更有效地诊断ISCF提供了依据。与正常情况相比,ISCF下的正序电压和电流在相位上发生了显著的变化,而ISCF下的负序电流和电压则通过实验显示出显著的振幅变化。因此,本文提出了一种新的故障指示器,利用正序电流与电压的相位差,以及负序电压的负序电流比的大小来检测故障。实验结果表明,所提出的故障指示器可以诊断出轻微的ISCF以及ISCF的严重程度。

1 理论基础

1.1 带有ISCF的提升机同步电动机的等效模型

图1表示在A相发生匝间短路的提升机电动机定子的等效模型。设N为每相的总匝数,n为短路匝数,则短路匝数比μ=n/N,表示故障相中短路匝数与总匝数之比,ISCF的严重程度随着μ的增加而增加。故障电阻Rf代表绝缘劣化,并与故障电流相关,ISCF的严重程度随着Rf的降低而增加。当μ接近1并且Rf接近零时,故障成为完全的匝间短路故障。 总之,ISCF严重性随着μ增加或Rf减小而增加。

图1 A相中具有ISCF的提升机电机定子等效模型

1.2 正序和负序分量

对称分量是三相系统失衡的重要指标之一[10]。在对称分量中,相电流和相电压的正序分量和负序分量由以下等式表示

(1)

(2)

(3)

(4)

式中ips和ins分别为正序电流和负序电流。ia,ib和ic分别为a,b和c相的定子绕组电流。同样,vps,vns分别为正序和负序电压。va,vb和vc分别为相a,b和c的定子绕组电压。

2 仿真验证正负序列故障特征

2.1 仿真模型的建立

为了研究正序分量和负序分量的特性,搭建了提升机同步电机模型如图2所示。电机参数如表1所示。电机型号为TBPS710—8,有8个极,84个槽,每相有4个并联支路,每条之路由7个串联的集中绕组组成。采样频率为2 kHz。在452 r/min的旋转速度下,对其进行正常和故障的仿真实验。ISCF的不同严重程度通过改变μ和Rf来实现,具体见表2和表3。因此,结合表2和表3的值,进行了12例ISCF测试。当μ= 0.143和Rf= 2 Ω时,ISCF最轻,当μ=0.429和Rf= 0.1 Ω时ISCF最严重。

图2 TBPS710—8型同步电机模型

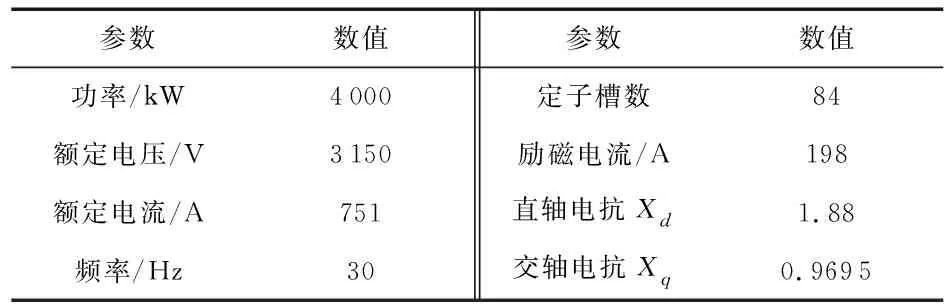
表1 试验中同步电机的参数

表2 不同μ下的故障程度

表3 不同Rf下的故障程度 Ω

2.2 ISCF下的正序和负序信号

为了保证ISCF正负序分量的清晰特征,试验了比较严重的ISCF的情况,例如(μ,Rf)=(0.286,0.1 Ω)和(μ,Rf)=(0.429,0.1 Ω)的情况,如图3。图3(a)表示的是当μ变化时的正序电流和电压的时域波形。与正常情况相比,正序电流和电压的幅度变化很难观察到,而正序电流和电压的相移却很容易观察到。图3(b)描述了负序电流和电压的时域波形。如图3(b)所示,负序电流的幅值随着μ的增大而增大；负序电压的幅值随着μ的增大而减小。这意味着当μ变化时正序分量的相位发生偏移,负序分量的幅值发生变化。

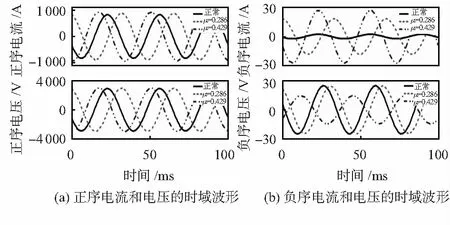
图3 不同μ下,正序/负序电流和电压的时域波形

针对图3情况的相同原因,可以进一步研究相对严重ISCF的情况,比如图4(a)((μ,Rf)=(0.429,0.5 Ω))和图4(b)((μ,Rf)=(0.429,0.1 Ω))。图4(a)表示不同电阻Rf下正序分量的波形。从图4(a)可以明显看出,正序分量的相位随着电阻Rf的减小而逐渐变化的,然而其故障状态下的幅值与正常情况下没有明显差别。图4(b)为不同电阻Rf下正序分量的时域波形。正常和故障状态下的负序电流,从图中可以看出,随着电阻Rf逐渐减小,负序电流的幅值反而逐渐增大,然而在正常和故障状态下负序电流的相序变化并不明显;同样地,正常和故障状态下的负序电压,其变化趋势和正序基本一致。

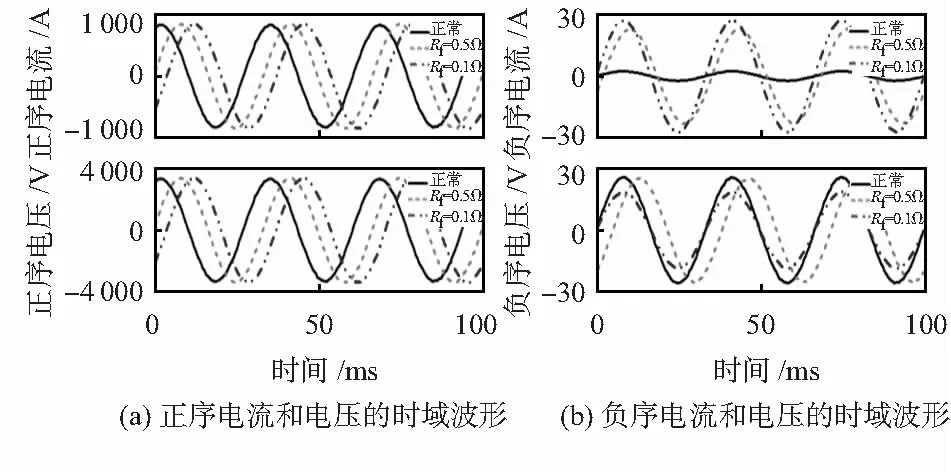
图4 不同Rf下,正序/负序电流和电压的时域波形

总之,一旦出现了轻微的ISCF,正序分量的相位和负序分量的幅值都会发生改变。

3 针对ISCF分析提出的故障指标

3.1 新型故障指标选择的分析

正如2.2节中提到的,当轻微的ISCF出现时,正序分量相位和负序分量幅值均发生变化。由此,可以定义以下参数

φ=∠ips-∠vps

(5)

(6)

式中 φ为正序电流和电压的相位差,Z为负序电压和电流比值的幅值。

通过研究功率因数和阻抗的定义,定义了式(5)和式(6)。φ代表正序分量相位变化,Z代表轻微的ISCF下负序分量的幅值,因此当轻微的ISCF出现时,φ和Z会发生变化。然而,在轻微的ISCF指标中,φ和Z需要是标幺值。φ和Z的标幺值如下所示

(7)

(8)

式中 φN和ZN为φ和Z的标幺值,且没有单位。

3.2 故障指标的提出

为了确定一个能够诊断出早期探测和ISCF严重程度的轻微ISCF的故障指标,提出一个新型故障指标

(9)

这种新型故障指标不仅包括相位和幅值的信息,而且仅利用电压和电流。因此,这种新型故障指标简单易行,适用于提升机电机参数不确定或无传感器控制的情况。在正常情况下,故障指标几乎为零；而当轻微ISCF严重时,故障指标变大。

4 实验验证

图5(a)表明了故障指标为什么可以同时利用相位和幅值。图5(a)是φN和ZN随μ变化的示意图。ZN是仅与幅值有关的指标,其值随着μ的增大而减小。相比之下,φN是仅与相位有关的指标,但它不能检测出ISCF的严重程度。图5(b)描绘了φN和ZN随Rf变化的示意图。在Rf变化的情况下,ZN是很难区分Rf= 0.5 Ω和Rf= 0.7 Ω。同样地,φN很难区分Rf=0.1 Ω,Rf=0.5 Ω和正常情况。因此,故障指标应该同时使用相位和振幅来诊断ISCF的严重程度以及轻微的ISCF的存在。

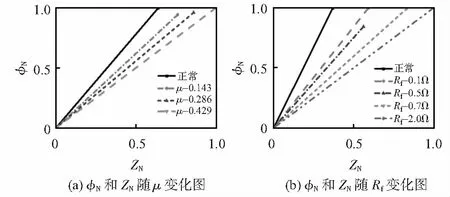
图5 实验结果

表4和表5代表452 r/min工况下的故障指标。表4为不同μ下的故障指标,在正常条件下,故障指标几乎是零,并且随着μ增加而增大。轻微ISCF的故障指示值指标甚至可以明显区别电机的正常情况。表5为不同Rf下的故障指标,故障指标随着Rf的减少而增大。在轻微的ISCF中,实验结果显示了类似表4的趋势。这些结果表明,该诊断方法在ISCF严重程度和轻微的ISCF中都是有效的。

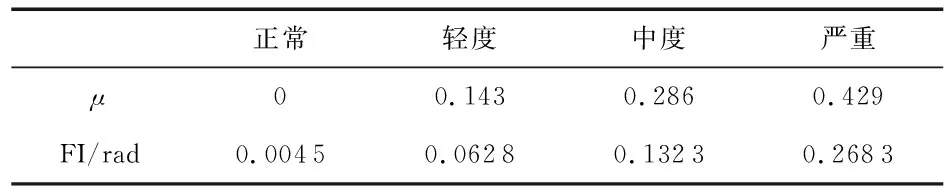
表4 Rf=2Ω时,故障指标随μ变化情况

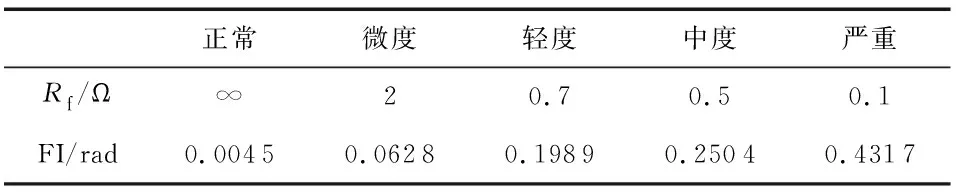
表5 μ=0.143时,故障指标随Rf变化情况

5 结 论

通过对轻微ISCF下正负序列特征的分析,本文提出了一种新型的故障指标。实验结果表明:

1)所提出的故障指标不仅能够成功地诊断出ISCF的严重程度,而且还能诊断出轻微的ISCF。

2)该方法是一种基于信号的方法,仅通过电压和电流信号就可以诊断轻微ISCF,不需要模型参数和旋转角度。

3)该诊断方法可以有效地应用于由于老化或电机故障导致提升机电机模型不确定性或无传感器控制等领域。