基于改进IMM运动模型的室内定位算法*
贺军义, 郭 凯, 张 敏
(1.河南理工大学 计算机科学与技术学院,河南 焦作 454002; 2.河南理工大学 教务处,河南 焦作 454002)
0 引 言
由于GPS信号在室内复杂环境中受到遮挡而迅速衰减,导致该技术无法有效地应用到室内定位领域[1]。近年来,国内外学者对室内定位技术展开了大量的研究。室内定位方法种类繁多,如基于到达角度(angle of arrival,AOA)、基于接收信号强度(receive signal strength,RSS)、基于到达时间差(time difference of arrival,TDOA)。由于TDOA算法具有成本低、效率高等特点故成为室内定位最常用的算法[2]。
对定位数据处理是机动目标跟踪中的关键环节,要想实现对目标稳定精确的跟踪首先要准确地预估目标的运动模式[3]。经过几十年的发展,传统卡尔曼滤波算法已经衍生出多种版本。单模型(single model,SM)滤波器在线性高斯模型条件下得到较好的跟踪效果,但很难精确地适应整个运动过程,容易造成滤波器的发散[4]。基于该问题有关学者后来提出了交互式多模型(interactive multi-model,IMM)算法,该算法使用多个机动或非机动模型来描述工作过程中可能的状态,最后通过有效加权融合进行系统状态估计,较好地解决了SM估计误差较大的问题。但固定结构多模型(fixed structure multiple model,FSMM)算法的模型集是固定的,只有增加模型数量才能提高跟踪精度;变结构多模型(variable structure multiple model, VSMM)通过切换不同模型组使得模型集动态变化[5]。无论FSMM还是VSMM,提高跟踪精度必定会增加运算量,降低跟踪的实时性[6]。因此,SM算法和IMM算法都存在特定缺陷。
针对传统IMM算法融合模型集过多导致效率降低的问题,本文提出了一种基于改进IMM运动模型的融合Singer的交互式多模型(Singer-insetted interactive multiple model,SIMM)跟踪算法。该算法只需融合非机动模型和基于加速度为时间相关的Singer模型,SIMM算法不仅能够根据目标的实际运动状态实时地调整模型概率,选择与目标运动相匹配的模型,还能根据目标机动强弱来调整Singer模型的参数。各模型之间的转移由Markov转移矩阵确定。本文将在高机动运动情景下通过对比IMM算法和SIMM算法来验证SIMM算法的性能。
1 TDOA定位模型
TDOA又称作双曲线定位方案,其定位原理如图1所示[7]。基于双曲线的数学特性,以两个定位基站为双曲线焦点,基站位置坐标已知,以标签到两基站的距离差为实轴画一对双曲线。同理,再次选取其他基站也可与主基站画出双曲线,移动标签的坐标为两曲线相交的位置。TDOA量测需要定位系统通过待测节点向各定位基站发送无线电脉冲,计算出待测节点到达从基站与主基站的时间差,进而得到距离差进行定位。
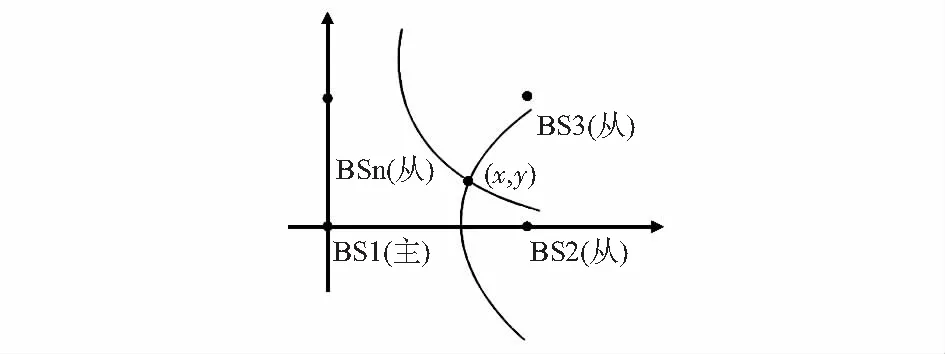
图1 TDOA定位原理
将移动标签坐标设为(x,y),运动环境内装N(N>3)个定位基站,坐标为Pi(xi,yi),i= 1,2,…,N。主基站为1号基站,从基站与主基站进行数学计算得出TDOA值[8]
di,1=cti,1=di-d1,i= 1,2,…,N
(1)
式中di为第i号基站到移动标签距离值;ti,1为移动标签到i号基站和1号基站的时间差值,将时间差值与光速c相乘得到其距离差值di,1。另根据二维空间的欧氏距离公式有
(2)

(3)
式中xi,1=xi-x1为基站i与基站1横坐标的差值;yi,1=yi-y1为基站i与基站1纵坐标的差值。显然式(3)是关于未知数x,y和d1的线性方程。
2 SIMM算法工作原理
获取到TDOA量测定位结果之后,需要对运动标签进行跟踪。由于目标运动的不确定性,无法通过单一的运动模型描述其实际的运动状态。本文将建立运动环境信息与运动模式预测、模型集之间的关系,并应用于IMM算法。
2.1 运动模型设计
如何对加速度进行准确可靠地描述是解决机动目标建模问题的关键。本文将Singer模型融合到IMM模型集当中,较好地解决了预估目标运动状态不准确的问题。在Singer模型中,假设机动目标的加速度a(t)服从一阶时间相关过程,a(t)的时间相关函数为Ra(τ),可以表述为指数衰减形式[9]如式(4)所示
(4)

(5)
式中Amax为机动目标加速度的极大值;Pmax为机动目标加速度为极大值时发生概率;P0为目标非机动时的发生概率。应用维纳—柯尔莫哥洛夫白化法对加速度a(t)的时间相关函数Ra(τ)进行白化后,机动目标的加速度a(t)可以用一阶时间相关的白噪声模型表示,如式(6)所示[11]
X(k+1)=F(k)X(k)+V(k)
(6)
不难看出,Singer模型本质上是一种先验思想。
2.2 跟踪算法设计

3 SIMM算法实验与分析
3.1 实验设置
在室内环境中,定位目标的实际运动状态通常包含多种,其中包括匀速运动、匀加速运动、变加速运动等。本文对此要求在室内环境设计了路径实验对比检验传统IMM与SIMM的跟踪效果,预设路径及基站分布如图2所示。

图2 实验环境及路线设计
实验区域设置在25 m×12 m的室内环境下,本实验使用4基站和1标签采集定位数据,4个基站分别分布在实验区域的4个顶点,并将(0,0)处基站设为主基站。首先,运动标签按预定路线从点A(20,120)处沿y轴负方向运动8.5 m;紧接标签从点B(20,35)处开始做变加速运动;最后,标签从点C(190,37)处沿x轴正向做匀速直线运动。
3.2 运动模型选择

传统IMM算法同样融合3个运动模型:模型一为非机动模型,过程噪声方差为0;模型二选取机动模型,系统扰动噪声方差为Q=0.001I2×2;模型三选取机动模型,系统扰动噪声方差为Q=0.014 4I2×2,各算法运动模型组合设计如表1所示。为控制实验变量的唯一,两种算法控制模型转换的Markov链转移概率矩阵都为

设定各模型在采样开始时刻的概率分别为μ1=0.8,μ2=0.1,μ3=0.1。

表1 模型组合设计
3.3 实验结果分析
实验测定了运动标签在实验场地中的运动轨迹,将SIMM算法与传统IMM算法进行比较并分析了实验结果,实验结果如图3~图5所示。本文采用位置的误差均值和误差标准差来评估算法性能。
定义滤波误差均值
定义滤波误差标准差

图3展示了标签运动的真实轨迹和观测轨迹还有两种算法的滤波轨迹。结果表明,在沿y轴运动初期,两种滤波算法对于目标误差的消除作用是非常明显的,其轨迹相比于观测值更加平滑,而且两种算法的滤波效果并无明显差别。但在坐标(30,20),(110,80),(180,30)dm处滤波值相对于真实值都产生了“滞后”现象,甚至短时间内造成误差大于观测值。这是由于标签出现急转弯、急停等高机动运动时算法融合的运动模型无法立即适应目标的运动状态,使得干扰信号统计学特性发生了改变。由图3可以看出,在滤波出现“滞后”现象后传统IMM算法会逐渐恢复其功能,但短时间内会造成极大误差;SIMM算法虽然在转弯时也出现了“滞后”现象,但相比较传统IMM算法,其造成的误差更小,并且收敛速度明显快于传统IMM算法。
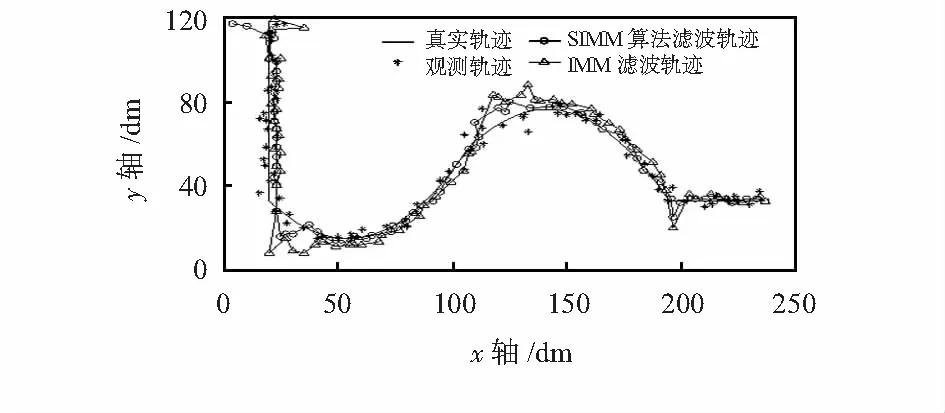
图3 不同算法滤波轨迹
图4展示了不同坐标轴下两种滤波算法的估计误差均值。可以看出无论是x轴还是y轴SIMM算法的滤波精度都明显高于传统IMM算法,当目标转弯出现滤波发散时前者的收敛速度也更快,而且在标签做加速运动时SIMM的滤波效果更为显著。

图4 不同算法估计误差均值
图5给出了不同算法的估计误差标准差,该指标反映了两种算法滤波结果的平滑程度。由该图可以得出,当采用SIMM算法时,相比于传统IMM算法,前者的跟踪效果更加稳定,滤波轨迹更加平稳。

图5 不同算法估计误差标准差
表2数据是对所有采样点的滤波结果求误差均值和误差标准差,分析表中数据可以得出无论是滤波精度还是滤波稳定性SIMM算法都有一定的优势。
综上所述相比于传统IMM算法,显然文中提出的SIMM算法滤波效果更优。
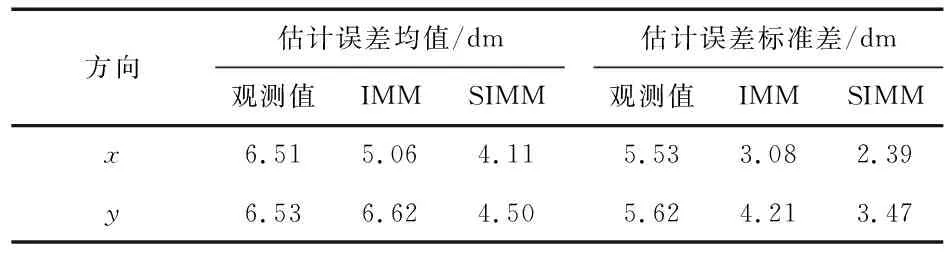
表2 两种算法对移动标签定位精度比较
4 结束语
对于机动目标而言,目标运动状态的快速转变会导致滤波算法运动模型匹配失效,短时间内会急剧增加滤波误差。为提高跟踪精度,一方面研究了如何减小初始定位误差,本文利用TDOA算法精度较高和计算复杂度较低的特点,有效降低了定位时产生的误差;另一方面研究了如何优化IMM算法的适应性和精确度,在传统IMM算法的基础上,结合Singer模型的自适应性特点,提出了SIMM算法,进一步提高了对机动目标的跟踪性能。实验表明,本文提出的算法能够有效降低目标在强机动运动状态下定位的误差。但算法仍然具有局限性,由于TDOA算法的特性,当实验在非视距环境下定位误差较视距环境下会变大,该问题将在下一步工作中解决。

