拓展模型迁移 培养数学应用能力——以一道典型力学题的拓展教学分析

杨 勇

（贵州省安顺市关岭民族高级中学，贵州 安顺 561300）

对物理问题的探究与拓展，有助于促进知识的建构、知识的迁移应用、着力于面向解决实际问题的思维层次性发展，通过对物理问题的探讨与分析，对问题的拓展与迁移，对学生的学科素养的提升和创新思维能力的培养具有重要作用.同时物理解题的拓展与分析，促进学生创新思维能力的提升，优化学生创新思维，把核心素养教学目标落到实处.

1 例题呈现

如图1所示，一盛水容器绕竖直中心轴线匀速转动，试证明容器转动时，容器中的水面为一抛物面.

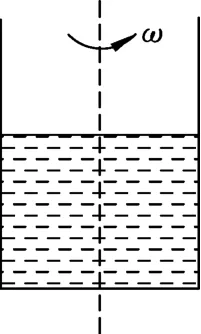
图1

2 典例问题教学分析

2.1 液体内部某点的受力分析

当容器以一定的角速度转动时，容器边沿的水会沿着边沿上升，中间部分水会往下凹.如图2所示，在液面的最低点建立如图所示的直角坐标系，在坐标原点沿着x轴方向的一段横截面积为ΔS，长度为x的水平液柱，假设水的密度为ρ，大气压强为p0，由于该液柱随着容器一起做匀速圆周运动，液柱左侧受到的压力为F1=p0ΔS，液柱右侧的压强p=p0+ρgy，所以右侧受到的压力为F2=（p0+ρgy）ΔS，则液柱随着容器做匀速圆周运动的向心力有左右两侧的压力差来提供可得F向=F2-F1.因此向心力F向=ρgyΔS.

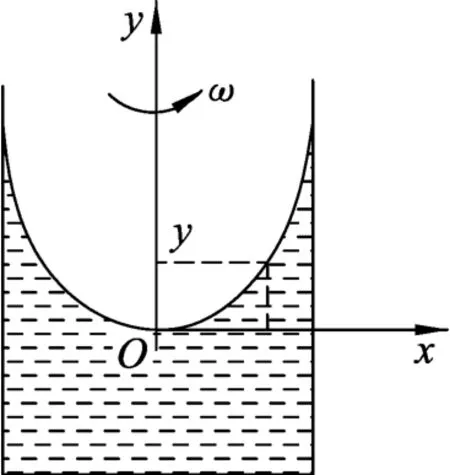
图2

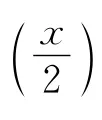
这是一条抛物线方程.由于在液面上所有的点都满足上式的方程，所以液面的曲线为一条抛物线，同理由这些线构成的面自然也是抛物面，因此容器转动时随容器一起转动的液体的表面为一抛物面.

2.2 液面上某点的受力分析

在液体表面取一质量很小的质点m，对该质点的受力分析如图3所示.该质点做匀速圆周运动的向心力由支持力与重力的合力提供，设支持力的作用线与y轴的夹角为θ，则受力F向=mg tanθ.该质点的横坐标为x，则

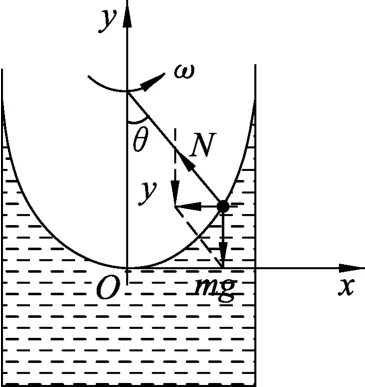
图3

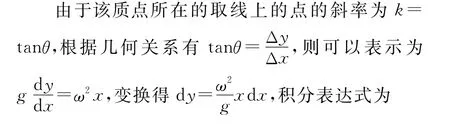
由于曲面上所有点的受力都有相同的特点，因此都满足上式的函数方程，由于上式是抛物线方程，则液面形成的即为抛物面.

2.3 引入非惯性系，对液面上任意质点静止的条件

如图4所示，选择随水一起转动的的容器为参考系，水相对于容器静止，引入惯性力f惯=mω2x，引入惯性力后液体表面所选的质点的受力平衡可知，

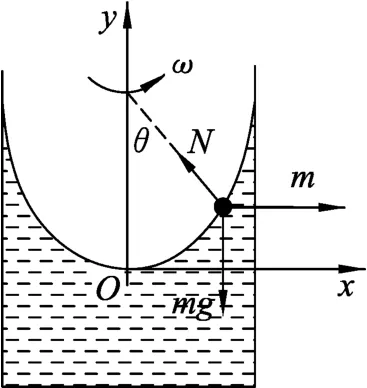
图4

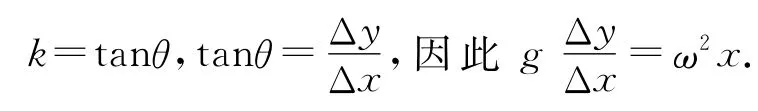
可得液体随容器转动时形成的液面为一抛物面.

以上从3个角度对容器中液体随容器转动时得到的曲面为一个抛物面，由于在某恒定的角速度转动时，液体的运动性质为同轴转动，角速度相等，应用角速度相等及液体受力特点结合圆周运动的性质，从受力角度、向心力来源、建立坐标等物理与数学的结合分析和证明液面为一抛物面.从不同角度对学生思维的激发和能力素养的培养，激发学生对问题的思考.

2.4 不同角速度下的曲面形状

3 拓展探究教学分析

3.1 绳子约束下的圆周运动对比与分析

如图5所示，用一根细绳长为l一端系一个小球，另一端固定，给小球不同的初速度，使小球在水平面内做角速度不同的圆周运动.根据圆周运动的特点有

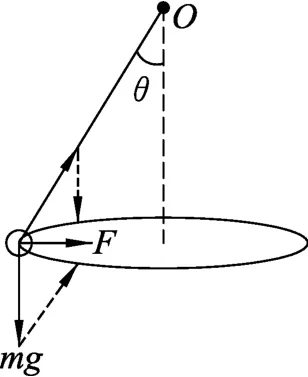
图5

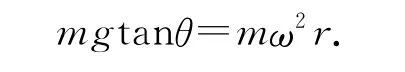
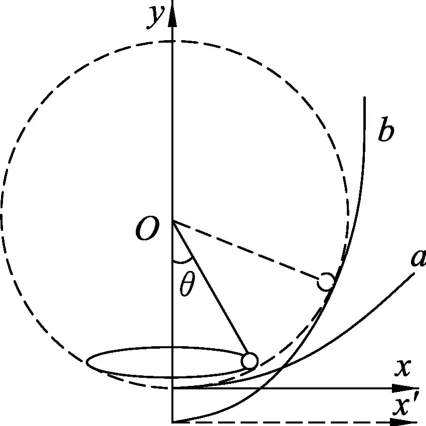
图6

3.2 锥面约束下的圆周运动对比与分析

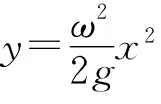
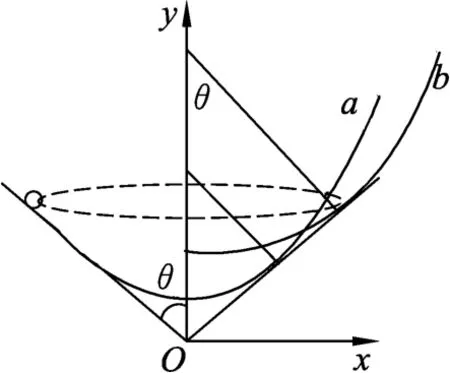
图7

3.3 杆约束下的圆周运动对比与分析

如图8所示，质量为m小圆环穿在光滑的杆上，小环能以相同的角速度ω在任意地方随杆做匀速圆周运动，结合所学的知识分析杆的形状.

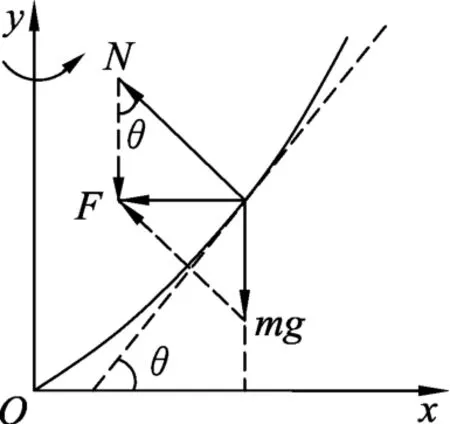
图8

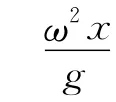
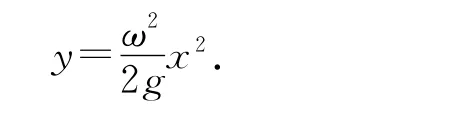
因此光滑杆约束与光滑面约束具有相同的特点，要让物体能以大小相等的角速度在任意位置做匀速圆周运动满足的条件必须是一个抛物形状的杆或者是一个抛物面，才能具有这样的特点.同理，可以发现为什么在光滑的锥面上小球做圆周运动的角速度不相等，如果能通过这样的一个抛物面的规律应用于相应具有一定约束锥摆的圆周运动中，可以使解决问题到达事半功倍.

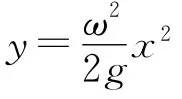
3 总结

对于以上的分析，从一到同轴转动问题的解法的分析，找到处理问题的方法，通过典例分析，联系常见的绳子约束、锥面约束、杆约束条件下的圆周运动的特点，找到具有相等的角速度的圆周锥摆运动满足一个抛物面的特点，从而培养学生分析问题，应用数学知识解决问题，应用知识迁移的学科素养.这样的拓展与分析在教学中能让学生的形成良好的思考习惯，创新思维能得到提升，同时，通过问题与知识迁移、模型对比等形式的教学分析和讨论，让学生主动获取知识，发展探究的能力，在解决探究问题的过程中加深对原有知识的认知结构，形成物理知识体系，克服思维单一、方法传统的保守习惯的弊端.让学生在探究过程中找到成就感，体验获得知识的喜悦，形成合作交流的团体，增强学生的集体意识，树立正确的学习观念，通过探究学习的过程体验，培养学生的创新思维，真正落实物理学科核心素养的教学目标.