燃爆压裂中压挡液柱运动规律的动力学模型*

吴飞鹏，蒲春生，吴 波

（中国石油大学石油工程学院，山东 东营 257061）

燃爆压裂中压挡液柱运动规律的动力学模型*

吴飞鹏，蒲春生，吴 波

（中国石油大学石油工程学院，山东 东营 257061）

针对燃爆压裂过程中压挡液柱受冲击运动机理的复杂性，假设火药燃气与压挡液柱存在完全气液接触界面，采用拉格朗日的微元分析方法，建立了由连续性方程、动量守恒方程、能量守恒方程组成的压挡液柱运动规律动力学模型，并给出了该模型与火药燃爆模型的耦合数值解法。经程序编制和实例计算表明，在综合考虑火药燃气对液柱的宏观推动作用、冲击压缩作用、液柱自身的动能分布及管壁对其摩擦阻力的影响后，火药燃烧过程中气液界面上升高度有限（实例计算不足0.1m），可起到很好的持压作用；但全过程中最高液柱位移较大（18.9m），水力振荡增效作用明显。研究成果对提高燃爆压裂的数值模拟精度具有一定促进作用。

爆炸力学；动力学模型；燃爆压裂；压挡液柱运动；动能分布

1 引 言

油水井燃爆压裂过程中的压挡液柱运动规律是影响火药燃爆能量分配及裂缝系统动态延伸的关键因素之一［1－3］，当前对于该问题主要是基于静力学分析或简化的动力学分析，将火药燃爆压力对液柱的作用分成初始冲击压缩作用和应力波传到液面后的刚体运动作用2个部分来分析，分别建立相关解析模型［4－10］。但是由于高能火药燃爆的强加载环境，整段液柱中各部分微元的运动速度差别非常大，由其所产生的动能影响和管壁对流体微元的摩擦阻力影响也非常大，不能忽略。由此，本文中，将综合考虑液柱运动过程中由速度分布造成的动能影响及管壁摩擦阻力影响，以液柱任意微小截面单元作为研究对象，利用质量守恒、动量守恒、能量守恒等条件，建立燃爆压裂过程中的压挡液柱运动规律动力学模型，据此可使压挡液柱运动规律的定量描述更符合实际情况。

2 压挡液柱运动物理模型

燃爆压裂过程中火药燃气对压挡液柱的作用机理很复杂，因此采用下列假设条件：（1）火药燃爆后燃气符合完全气体状态方程；（2）压挡液为牛顿流体；（3）燃气与液柱存在完全接触面，且液柱的压力为连续作用力；（4）全过程考虑流体微元动能变化和管壁摩擦阻力对液柱运动的影响；（5）液柱在井筒中的流动为等截面管流。

3 压挡液柱运动规律数学模型

当前研究流体运动一般采用质点分析法的拉格朗日法或空间固定观察站法的欧拉法［11］。本研究采用拉格朗日法，因此在一维流动中，选取各微团所在初始截面坐标位置x0作为拉格朗日坐标s。

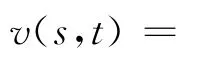
（1）连续性方程

当流体运动时，微团流体的截面位置在随时间变化，但此两截面包围区域中流体质量却不随时间变化。设l0为初瞬时t0两截面之间的距离，ρ0为两截面所限区域内的微团密度。经过时间t后，微元长度变为l，密度变为ρ，假设液体运动为等截面管流（A＝A0，A0、A分别为t0、t时刻的流体截面积），则液柱运动的连续性方程为

再由流体的压缩性，结合微元体压力和液柱压力的对应关系得

式中：β为流体体积压缩系数，Pa－1。

（2）动量守恒方程

流体微团受冲击运动时受到4种作用力的影响：

①下端界面处向上的压力p （x，t ）A；

②上端界面处向下的压力

式中：λ为牛顿流体管流摩阻系数，量纲为一；R为管柱内半径。由此应用牛顿第二定律，可得动量方程

③流体微元自身重力

④流体微元运动时受管壁的摩擦力

将式（3）～（5）代入式（6），并化简得

（3）能量守恒方程

在绝热、无粘的条件下，两截面包围区域内流体微团的熵值在运动过程中保持不变，则在流体微元运动过程中4种作用力对其作的功全部转变成流体微元自身的动能和弹性能。

由前面分析得出流体微元在运动中受到的合力为

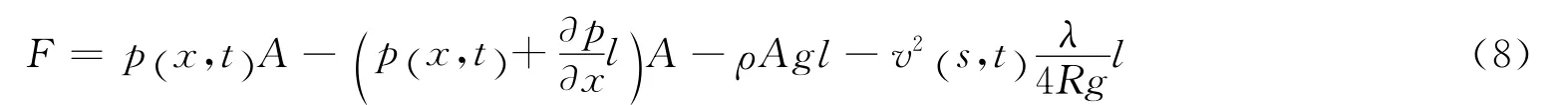
假设dt时间内，流体微元整体运动的距离为dx，微元长度变为l，则合力F对其做的功为

dt时间内流体微元的动能增量为

由位移、速度、加速度间关系得

将式（11）代入式（10）得

若压挡流体的弹性模量为E，可得在dt时间内流体微元的弹性能增量为

式中：dl为t时刻到t＋dt时刻的微元长度变化量。

最后综合式（9）、（12）、（13）得能量守恒方程为

（4）边界条件

若以pn（t）表示第n个流体微元t时刻所受的压强，则根据压挡液柱的运动规律可得边界条件为

式中：n＝1时pn（t）表示液柱底端微元所受的冲击压强；n＝M时表示t时刻应力波传到第M 个微元，M＝int（ct／l0）；HM为第M 个微元的上部液柱高度，HM＝HL－ct，其中HL为压档液柱总高度；n＝N时pn（t）表示液柱最上端微元的上端面所受压强，其值等于大气压（井口放开）。

4 压挡液柱运动规律模型求解

由上述分析得燃爆压裂过程中压挡液柱运动的数学模型为

其中的未知数为液柱各处压力p、微元流体密度ρ、微元自身长度l、微元位移x和微元运动速度v等5个参数，求解时模型（16）加上微元位移与微元自身长度变化的关系，共5个方程，可定量化求解任意火药燃爆压力、液柱条件和井身条件下的气液界面高度位移随时间的变化关系。

如图1所示，将整段液柱进行网格划分，进而对建立的数学模型（16）进行差分求解，以第i个微元网格为研究对象，分别对t时刻和t＋Δt时刻进行差分计算。

则连续性方程为

图1 液柱网格划分示意图Fig.1Schematic diagram of the gridded fluid column

动量守恒方程为

如图2，假设整个过程中液柱始终保持连续，则第i微元的位移与i－1微元的自身长度存在如下关系

图2 流体微元运动示意图Fig.2 Schematic diagram of the infinitesimal fluid column

结合冲击压力边界条件，从液柱底端第1个微元开始差分求解，就可求得任意时刻的液柱状态。

5 计算实例分析

利用建立的液柱运动模型，结合文献［12］给出的火药燃爆模型（式（12））、岩石起裂压力模型和文献［13］给出的燃爆压裂裂缝系统动力学模型，利用火药燃气的质量变化与压力变化可对各部分模型进行耦合求解，如此便可计算模拟火药燃烧、裂缝起裂延伸、压挡液柱运动组成的高能气体压裂全过程。利用该套理论编制计算程序，计算川高561井这一深层致密气井中，5km井深，50kg火药在1km清水液柱压挡情况下燃爆的燃气压力和底面气液界面的位移规律，如图3～5所示。

式中：Vg为药柱的燃烧体积，pw为井筒压力，w0为燃速系数（压力为1MPa时的燃烧速度），u为火药的燃烧速度；δ为t时刻药柱的燃烧长度，n为压力指数，ρ0为火药密度，Vr为燃烧室的自由容积；S0为装药的燃烧表面积，p为燃烧室内的平均压力，R为燃气常数，通常等于2.87J／（kg·℃）；f为火药力，T为燃烧室内的温度，cV为火药比热容。

式中：ps、pd为静、动载下岩心破裂压力，MPa；γ为动载加压速率，GPa／s。

式中：q（t）为火药燃气在射孔孔眼处泄流量，Lf（t）为t时刻燃爆压裂裂缝长度；W （x，t）为裂缝宽度；u （x，t）为火药燃气在裂缝壁面的渗流速度；p （x，t）为沿裂缝长度上的燃气压力分布；ρg为燃爆空间内火药燃气的密度；cg为火药燃气的比热容；dQ2（t）为某时间微元内裂缝系统内的流体增量；dQ3（t）为某时间微元内由裂缝壁面渗漏入地层的流体增量。

图3 裂缝延伸阶段液柱运动和燃爆压力的对应关系曲线Fig.3 Fracturing period corresponding curves between deflagate pressure and fluid column movement

由图3（图中H1为液柱底面运动的高度）可知，火药燃爆后液柱底面压力迅速上升，冲击应力波以液体中纵波的速度向上传播，应力波传到的地方液柱受压缩短，因此随着火药燃爆的进行，气液界面上升位移呈现变加速上升趋势；直到燃气压力趋于稳定（AB段），此时系统泄压速率与火药燃爆的产能速率达到平衡，新参与压缩的液柱段所受冲击压力近似相等，故在AB压力稳定阶段，液柱底气液界面呈现近似恒定速度地线性上升；当火药燃烧完全（B点）后，系统压力迅速下降，单位时间内新参与压缩的液柱高度恒定，但所受压力不断下降，因此液柱底面仍在上升，但此时为变减速运动。

图4 应力波传到液面前后的液柱运动和燃爆压力的对应关系曲线Fig.4 Stress wave propagating to the fluid surface period corresponding curves between deflagate pressure and fluid column movement

由图4可知，燃爆应力波在火药爆燃后705.7ms时传到液柱顶面，此时对应的液柱底面压力为9.95MPa，仍高于底面液压。此后随着应力波传出液面，参与压缩液柱的平均冲击力逐渐变小，因此此时液柱压缩到最短，之后液柱自身高度逐渐伸长，但液柱各部分微元将继续向上做变速运动，且此时的液柱底面微元的运动速度远大于液柱自身伸长速度，所以此后气液界面仍将向上做变速运动。

图5 液柱振荡过程中的对应关系曲线Fig.5 Corresponding curves during oscillation process

由图5可知，当冲击应力波传到液面后，伴随着自身长度的伸缩，液柱整体在惯性的作用下继续向上运动。此过程中由于重力、管壁摩擦力的作用，而且火药燃气本身也由于体积增大而迅速降压，液柱底气液界面上升速度逐渐减小，在6.75s时气液界面停止向上运动，气液界面上升到最高18.90m；此后，液柱在重力作用下下降，火药燃气压力上升，减缓液柱运动，到达最底端后又开始反弹，出现振荡，直至能量损耗完毕。

但需注意的是，图5中所示的液柱振荡曲线是在气液存在完全接触界面的假设条件下计算的，实际作业过程中随着时间的推移，液柱底面将出现气液混合作用，运动规律很复杂，需要进一步深入研究。但从燃爆压裂的火药开始燃爆到裂缝止裂阶段耗时仅为几毫秒（该实例2.5ms），气液混合作用极微，可忽略不计，故所建模型可作燃爆压裂过程耦合的关键模型之一。

基于燃爆压裂的瞬时性、复杂性，实时测试井底气液界面的位移很困难，但由于液柱参数对火药爆燃峰值压力影响很大，因此可通过测试实际爆燃压裂井的峰值压力来验证模型的可靠性如表1所示，表中h为压裂弹深度，H为液面高度，m为火药质量，pmax为爆燃峰值压力。

表1 实际燃爆压裂井的峰值压力对比表Table 1 Peak pressures of the actual blasting fracturing wells

从表1中可以看出，在装药量相当的情况下压挡液柱高度对峰值压力的影响显著；且在考虑液柱动能分布、管壁摩擦影响后的计算精度（平均92.737%）远高于解析算法精度（平均84.58%）；2种方法计算的峰值压力均小于实测值，这可能是由于实际情况下管柱在强冲击下会发生膨胀变形，使液柱流动为变截面流，从而加大了管壁对流动的阻力，导致燃爆峰值压力升高。

6 结 论

（1）综合考虑燃爆应力对压挡液柱的宏观推动作用、冲击压缩作用以及液柱的动能分布和管壁摩擦阻力的影响，以液柱任意微小截面单元为研究对象，利用质量守恒、动量守恒、能量守恒等条件，建立了燃爆压裂过程中的压挡液柱运动规律动力学模型，可为燃爆压裂系统耦合模型提供压力维持条件。

（2）利用动量守恒和能量守恒理论将火药燃爆模型、裂缝动态延伸模型和压挡液柱运动模型中的燃气压力、体积、质量耦合起来，建立了耦合数值求解方法，可定量计算任意火药和压挡液柱参数组合下的火药燃爆压力变化和气液界面位移变化的对应关系。

（3）实例计算结果表明：

①火药燃爆全过程中，冲击应力波一般未传到液柱顶面，液柱处于弹性压缩阶段，整体没有位移，且由于时间极短此阶段气液界面上升高度有限，可起到很好的持压作用；

②在冲击波传到液面后，液柱开始整体运动，火药燃气迅速卸压，当液柱底面上升到最高时井筒燃爆处压力降到最低；

③整个作用过程中气液界面可上移到较高位置（实例计算中为18.9m），表明燃爆压裂具有较好的水力振荡增效作用。

（4）本文中给出的压挡液柱运动动力学模型考虑因素更加全面，研究成果对提高燃爆压裂优化设计的精度具有一定促进作用。

［1］林英松，蒋金宝，孙丰成，等.爆炸技术与低渗透油气藏增产［J］.钻采工艺，2007，30（5）：48-52.

LIN Ying-song，JIANG Jin-bao，SUN Feng-cheng，et al.Exploding technology and low permeability reserroir improvement［J］.Drilling ＆ Production，2007，30（5）：48-52.

［2］石崇兵，李传乐.高能气体压裂技术的发展趋势［J］.西安石油学院学报（自然科学版），2000，15（5）：17-20.

SHI Chong-bing，LI Chuan-le.Development tendency of high energy gas fracturing（HEGF）technique［J］.Journal of Xi’an Petroleum Institute（Natural Science Edition），2000，15（5）：17-20.

［3］李文魁.高能气体压裂技术在油气资源开发中的应用研究［J］.西安工程学院学报，2000，22（2）：60-62.

LI Wen-kui.Researching and application on high energy gas fracturing technique used in the development of oil／gas resources［J］.Journal of Xi’an Engineering University，2000，22（2）：60-62.

［4］扬卫宇，周春虎.高能气体压裂设计关键因素量化分析［J］.钻采工艺，1992，14（6）：75-81.

YANG Wei-yu，ZHOU Chun-hu.Quantification analysis of the key elements to HEGF［J］.Drilling ＆ Production Technology，1992，14（6）：75-81.

［5］Yang David W.Numerical modelling and parametric analysis for designing propellant gas fracturing［R］.SPE 71641，2001.

［6］Yang David W，Qasmus R.Experiment study on fracture initation by pressure pulse［R］.SPE 63035，2001.

［7］柳贡慧，赵旭.复合射孔上部压井液运动机理试验［J］.中国石油大学学报（自然科学版），2008，32（6）：88-91；95.

LIU Gong-hui，ZHAO Xu.Movement mechanism experiment of top control fluid in compound perforation［J］.Journal of China University of Petroleum（Edition of Natural Science），2008，32（6）：88-91；95.

［8］赵旭，柳贡慧.复合射孔上部压井液运动理论模型研究［J］.钻井液与完井液，2008，25（3）：7-9；21.

ZHAO Xu，LIU Gong-hui.Theoretical modeling of the movement of the top killing fluids in complex perforation［J］.Drilling Fluid ＆ Completion Fluid，2008，25（3）：7-9；21.

［9］吴飞鹏，蒲春生，吴波.燃爆压裂中压挡液柱运动解析模型研究［J］.钻采工艺，2009，31（3）：82-85.

WU Fei-peng，PU Chun-sheng，WU bo.Analytical model of the pressurized liquid column movement in the HEGF［J］.Drilling ＆ Production Technology，2009，31（3）：82-85.

［10］赵旭，柳贡慧，李中权.复合射孔压裂火药燃爆后气液作用分析［J］.西南石油大学学报（自然科学版），2008，30（5）：141-144.

ZHAO Xu，LIU Gong-hui，LI Zhong－quan.High energy gas and control liquid action characteristics after deflagration in complex perforation procession［J］.Journal of Southwest Petroleum University（Science ＆ Technology Edition），2008，30（5）：141-144.

［11］王新月.气体动力学基础［M］.西安：西北大学出版社，2006：37-38.

［12］吴飞鹏，蒲春生，陈德春，等.高能气体压裂合理装药量的设计与应用［J］.石油钻探技术，2009，37（1）：80-83.

WU Fei-peng，PU Chun-sheng，CHEN De-chun，et al.Design and application of a reasonable charge of high-energy gas fracturing［J］.Petroleum Drilling Techniques，2009，37（1）：80-83.

［13］蒲春生，吴飞鹏，任山.气井高能气体压裂裂缝系统动力学模型研究［J］.武汉工业学院学报，2009（3）：13-16.

PU Chun-sheng，WU Fei-peng，REN Shan.The study of the fracturing system of the high energy gas fracturing process to gas well［J］.Journal of Wuhan Industry Institute，2009（3）：13-16

A dynamic model of the pressurized liquid column movement in the high energy gas fracturing process＊

WU Fei-peng，PU Chun-sheng，WU Bo

（College of Petroleum Engineering in China University of Petroleum，Dongying257061，Shandong，China）

According to the kinematical mechanism complexity of the impacted pressurized liquid column in the high energy gas fracturing process，we assumes that the completely contacted gas liquid interface exits.Then by using a Lagrange analytical method for studying a random liquid across-section，a dynamic model of the pressurized liquid column movement law is set up，which comprises continuity equation，momentum conservative equation and energy conservative equation.Based on the pressure and volume conservation during the process of powder conflagration and pressurized liquid column movement，a coupling numerical method for describing the gas-liquid interface movement law is established.Example calculations show that when considering the macroscopical propel and impact compression on the pressurized liquid column caused by deflagration，dynamic energy distribution of the liquid distribution and pipe column friction resistance，the interface ascending height is limited（less than 0.1min the example conditions）.This illustrates that pressurized liquid column has a good function of backing pressure.But in fact，in the fracturing process，the interface can reach a higher position（18.9m），which shows that in the later process，hydraulic oscillation produces an obvious synergistic effect.

mechanics of explosion；dynamic model；high energy gas fracturing process；pressurized liquid column movement；dynamic energydistribution

8August 2009；Revised 29November 2009

WU Fei-peng，upcwfp＠163.com

（责任编辑 曾月蓉）

O389；TE357.2 国标学科代码：130·35

A

1001-1455（2010）06-0633-08

2009-08-08；

2009-11-29

国家自然科学基金项目（50774091）；国家西部开发科技行动计划重大科技攻关项目（2005BA901A13）

吴飞鹏（1983— ），男，博士。

Supported by the National Natural Science Foundation of China（50774091）；the Key Technology R＆D Program（2005BA901A13）