回归真实探究,促进深度学习
——以探究“自由落体运动”教学为例
刘 明
(福建省厦门第六中学,福建 厦门 361000)
1 问题的提出
《高中物理新课程标准(2017版)》对实验探究部分的教学建议中指出:应在实验中培养学生发现和提出问题能力;应通过实验提高学生制订计划的能力;要避免让学生按给定步骤进行符合预期的虚假“探究”;在收集实验信息时,要尊重实验事实,不应只把注意力集中在与探究假设相符的物理事实上,还需要观察和收集那些与预期结果相矛盾的信息;要从交流内容的组织和陈述形式等方面提高学生交流和表达能力;应在实验中发展学生依据证据、运用逻辑和现有知识进行科学论证和解释的能力等.[1]
然而,现实中的实验教学仍然存在较大的问题,讲实验、看实验、练实验的情况普遍存在,学生的实验探究多数情况下停留在学生按部就班,根据教师和书本提供的实验方案和步骤,匆匆完成实验,得出实验结论.在实验过程中既没有方案设计;没有数据分析论证;甚至实验中得出与期望的实验事实不相符也完全不理会,更没有深入的误差分析及实验改进的探究.这样的实验探究过程,是名符其实的“虚假探究”,教师的教学停留在为学生完成实验而做实验,实验的教育教学功能没有得到充分发挥,与通过学科教学培养学生核心素养的宗旨背道而驰.[2]
2 促进深度学习的实验探究
2.1 基于知识基础,引导方案设计
深度学习是建构知识意义的学习,学习者把新知识与已有的知识经验联系起来,在已有知识结构的基础上建构新知识,丰富或重构原有的认知结构.[3]
学生已有利用打点计时器和纸带研究匀变速直线运动的经验,在此基础上,引导学生将斜面上的小车下滑改为竖直方向的自由下落,同时从减小阻力的角度引导学生将小车换为体积小,密度大的重物(使下落重物的重力远大于阻力),构建一个自由落体运动实物模型如图1,合理设计出实验装置,在构建过程中深化自由落体运动模型的理解和认识.

图1
纸带上记录了物体下落的时间和相应的位移,引导学生回顾根据纸带分析重物下落是否为匀变速直线运动的方法如下.
(2)逐差法:依据匀变速直线运动的推论相邻相等时间位移差Δs=a T2=定值,判定该运动是否为匀变速直线运动并求出加速度a.
(3)v-t图像法:若能根据纸带求出纸带上选取的各计数点的瞬时速度v,作出v-t关系图像,若是直线则说明该运动是匀变速直线运动,并可以根据图像的斜率k=a,求出加速度a.
由于纸带记录的是时间和距离,速度不是直接测量量,在判定纸带的运动性质之前不能直接求出纸带上对应计数点的瞬时速度,不选用v-t图像法.
2.2 基于技术融合,优化数据处理
“提高物理教学水平,发展学生物理学科核心素养,离不开信息技术与物理学习的融合”.[1]在实验的数据分析处理中,把利用Excel软件自动计算和绘制相关图表的方法教给学生,简化实验过程中繁琐的实验数据计算和处理,将实验重点放在实验方案设计及实验结果的评估上,不仅节约时间成本,也有利于学生通过图表分析强化匀变速直线运动规律的深度理解.
选取一条实验中点迹清晰的纸带,以实验中打点计时器打的第1个点为计时起点(计数点0),并取各计数点间的时间间隔T=0.04 s,如图2为选取纸带的前半部分.

图2
(1)h-t2图像法:将测量数据填入表1.

表1 探究自由落体运动数据记录
利用Excel软件作图和图像趋势线方程作出h-t2关系图像,如图3.

图3 h-t 2关系图像
图3中的h-t2关系图像是直线可判定物体下落是匀变速直线运动,并根据图像的趋势线方程中的斜率,求出加速度a=8.72 m/s2.学生可发现该值与当地重力加速度实际值相差甚远.
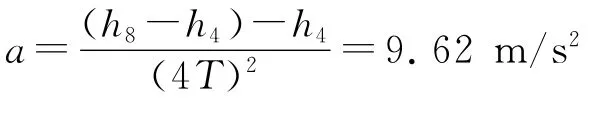
同一条纸带,两种分析处理方法的结果相差如此大?这样的实验结果冲突,激发学生探究兴趣,引发对实验的进一步分析思考.
2.3 基于证据分析,引发深度思考
表1的数据是选取其中一组学生的实验数据分析的结果.在操作正确的前提下,同一组数据两种不同的处理方法得到的实验结果相差较大.出现与预期不符的实验结果,绝不能简单以“实验总是存在误差”为由含糊带过,要引导学生尊重客观事实,深度追寻产生问题的原因,充分收集利用真实客观的证据,引发学生的深度思考.
2.3.1 对比纸带发现问题
对比几条不同组别学生打出的纸带如图4,引导学生观察,各组选取的相同计数点的点位和点距并不相同且相差较大.

图4
提出问题:
(1)是否是因为装置不同引起的?
请学生利用同一装置打出几条纸带,发现上述问题依然存在.
(2)纸带释放瞬间和打点计时器打0点的瞬间相同吗?
引导学生讨论交流分析总结出:在未释放纸带前纸带静止,打点针在纸带上重复打点,在纸带上留下一个黑而粗的计数点0点.若释放纸带瞬间打点计时器恰好打点,则选取的计数点1为纸带释放后打的第3个点,和计数点0的时间间隔T等于0.04 s;若纸带释放瞬间不是打点计时器打点瞬间,则选取的计数点1为释放纸带后打点计时器打的第2个点,因释放纸带后打的第1个点与计数点0的间隔要小于0.02 s,所以计数点1与计数点0间的时间间隔小于0.04 s,这取决于释放纸带瞬间与打点计时器打第1个点的时间间隔,若这个时间间隔为0.01 s,则计数点1与计数点0的时间间隔为0.03 s,小于选取的计算值0.04 s;若因为纸带释放瞬间与纸带上打第1个点的时间间隔太小(如0.003 s),导致释放纸带后打的第一个点被计数点0覆盖,则选取的计数点1为纸带释放后打的第3个点,则计数点1与计数点0的时间间隔为0.043 s,大于选取的计算值0.04 s.
2.3.2 根据图表数据分析误差

(2)逐差法:在表1中计数点1与起始点0之间的位移差Δs=0.0123 m,明显小于其它两段相邻相等时间T内Δs的值,这也是因为时间间隔的小于0.04 s,也就是这个时间间隔和其它计数点间的时间间隔是不相等的,不符合“相邻相等时间”的条件,因而存在误差.
2.4 基于方案改进,实现思维进阶
深度学习是学习中分析、综合、创造等高阶思维能力运用于学习过程,监控和反思学习过程中实现思维进阶.
学生从证据分析中发现,出现较大的实验误差的主要原因是由于释放瞬间并非计时器打点瞬间,计数点1与计数点0的时间间隔并不等于0.04 s,只要剔除这段数据,并通过实验数据处理方法的进一步改进优化,即可减小误差.
2.4.1 图像法方案改进
以原纸带的计数点1作为计时起点0,记录相关数据,如表2.
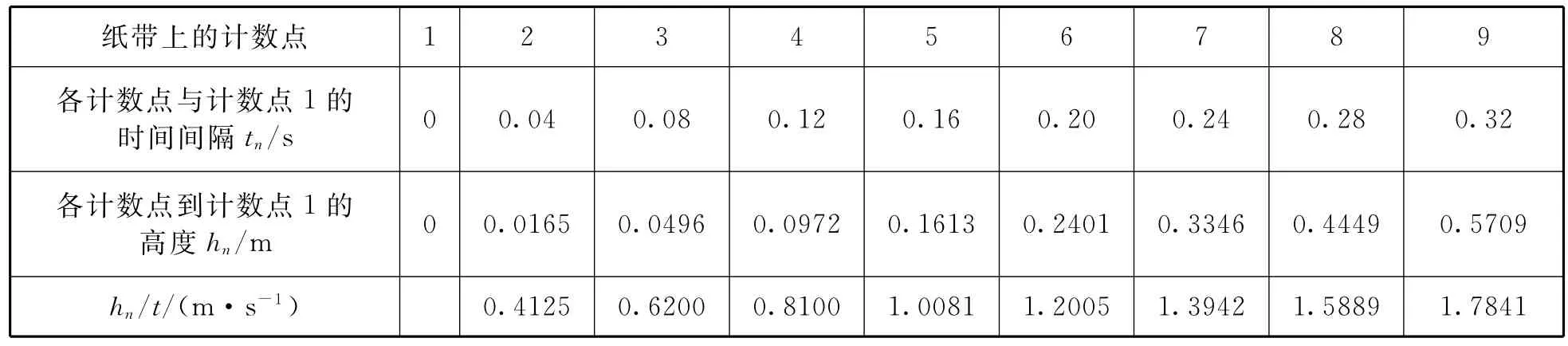
表2 探究自由落体运动数据记录

图5 h/t-t关系图像
根据图像的斜率,求出加速度a=9.76 m/s2,对比图3中h-t2关系图像所求加速度值,误差减小,与当地重力加速度实际值接近.
2.4.2 逐差法计算结果
重物下落过程中存在空气阻力和打点计时器对纸带的阻力的作用,使实验必然存在系统误差;实验中距离测量的偶然误差对实验的影响也不小;时间测量方面,打点计时器频率不稳定也会引入误差.但利用图像处理数据,不仅更加简洁直观的反映了纸带的运动情况,还可以剔除误差较大的点,在计算加速度的时候综合考虑每一个数据,大大的减小了实验误差.
3 结束语
在探究自由落体运动中,通过有效融合信息技术,简化数据处理过程,把探究的重心放在实验方案设计、证据收集与分析、科学论证与交流等方面,学生真实地经历这样的探究过程,在深度体验中发现问题、在深度分析中提出问题、在深度思维中解决问题,实现深度学习,提升学生核心素养.

