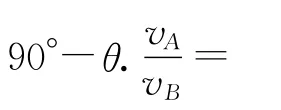一题多解探骊高中物系相关速度分析

孙朝晖

（宁波市北仑中学，浙江 宁波 315800）

例题.木棒A端靠在竖直墙壁上，B端在水平地面上，当木棒A端沿墙壁自有下滑至棒与水平面成θ角瞬间，如图1所示，求A、B两端速率之比vA∶vB.

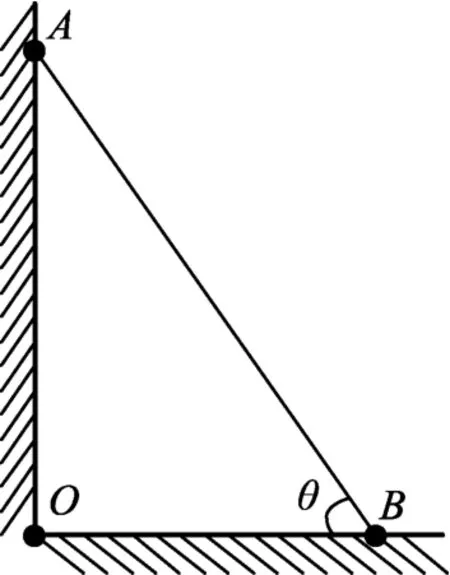
图1

答案：vA∶vB=cotθ.

国内外中学物理竞赛中多见求解物系相关速度，或解题的“瓶颈”卡在物系相关速度的试题.这类问题往往叙述简洁而条件隐蔽，情景相像而方法各异，使解题者思路混乱，无从下手.对于上述这道典型的物系相关速度问题，通过对该题进行一题多解，能对刚体物系相关速度有深刻认识；同时加深对下述7种解法思路的理解，在碰上其他涉及物系相关速度的问题时，灵活选取合适的方法往往能事半功倍.

方法1：速度分解法.

充分利用物系相关速度之间的关系简捷求解.对于本题，如下结论很有用：刚性杆、绳上个点在同一时刻具有相同的沿杆、绳方向的分速度.因此，就本题而言，A、B两点在沿棒方向上具有相同的速率，即vAsinθ=vBcosθ（速度分解前后大小如图2所示），从而化简可得vA∶vB=cotθ.

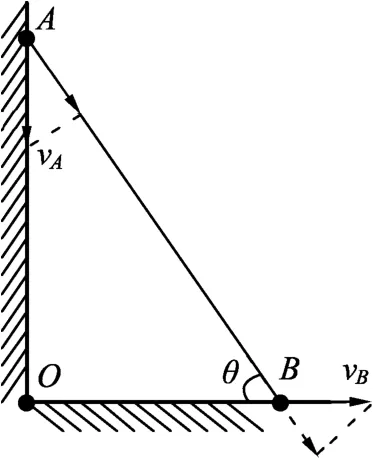
图2

方法2：速度 位移转化法.

极短且相同的时间内，物体的末速度为瞬时速度，可用极短时间内的平均速度代替瞬时速度.而运动时间相同，故物体的位移比等于速度比.如图3，木棒在极短时间Δt内，上端由A点滑落到A′点，下端由B点滑落到B′点.由几何关系，木棒长度不变AB=A′B′，极短时间对应Δθ→0.过A′作A′A″⊥AB 交于A″，过B作BB″⊥A′B′交于B″.

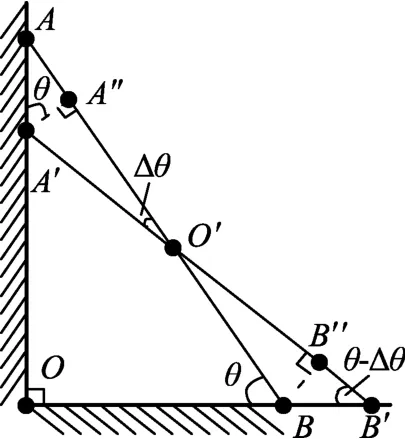
图3

AB=AA″+A″O′+O′B=AA′sinθ+A′O′cosΔθ+O′B；

而AB=A′B′=A′O′+O′B″+B″B′=A′O′+O′B cos Δθ+BB′cos（θ-Δθ）.极短时间对应Δθ→0，故cosΔθ=1，cos（θ-Δθ）=cosθ.可得AA′sinθ=BB′cos（θ-Δθ）=BB′cosθ，从而vAΔt sinθ=vBΔt cosθ，最终解得vA∶vB=cotθ.

方法3：平动-转动复合法.

刚体运动具有这样的特征：刚体各质点自身转动角速度总相同且与基点的选择无关.因此木棒A点的运动可看做水平向右速度为vB的平动和点A绕点B的逆时针转动（角速度为ωA=ω）的复合；木棒B点亦可同样处理（图4）.由A点合速度vA和分速度ωL和vB的关系可知：vA=ωL sinθ，vB=ωL cosθ，从而得到vA∶vB=cotθ.

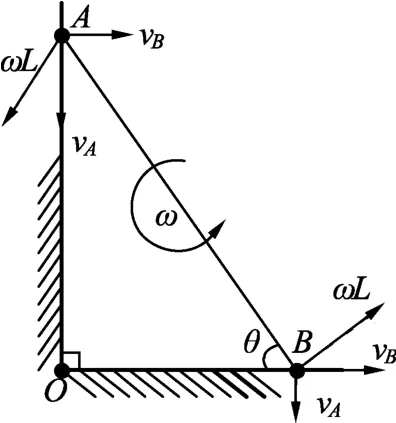
图4

方法4：瞬心法.

一个刚体做平面运动时，有且只有一个点是瞬时静止不动的，这一点称为瞬心（瞬时转动中心），木棒上所有点关于瞬心作圆周运动的角速度都相等.因此瞬心必定在各点速度矢量的垂线上，且各点的速度大小与其距离成正比.由此很容易确定瞬心的位置，同时利用瞬心知识来解题有时候特别方便.

如图5所示，过点A、B分别作速度v A和v B方向的垂线，两垂线交于点C，则可证明C为木棒沿墙壁下滑的瞬心.此时木棒上的点A、B均绕C作圆周运动，两者角速度相等，记为ω.也可认为该时刻三角形ABC绕点C逆时针做角速度为ω的圆周运动.于是，v A=ωAC，v B=ωBC，而BC／AC=tan∠CAB=tanθ，最终可解得v A∶v B=cotθ.

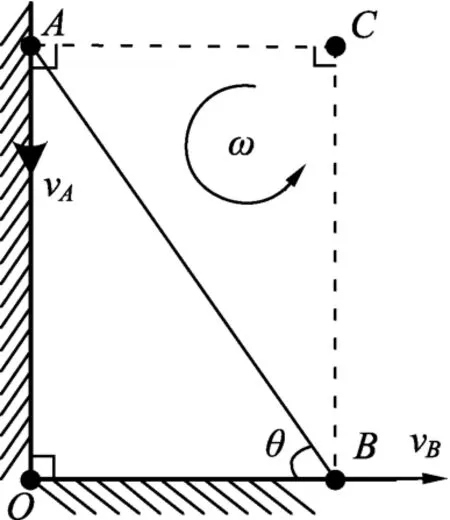
图5

方法5：微分法.

如图6所示，设AO=y，BO=x，则x2+y2=L2，y／L=sinθ.以下通过对x、y对时间的微分将路程转化为速率.

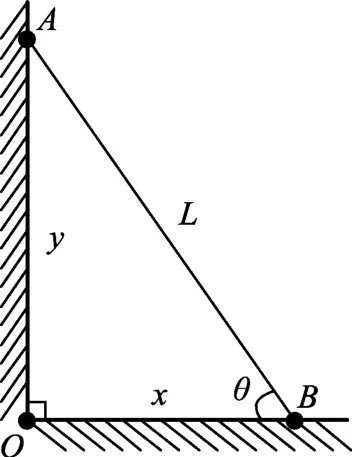
图6

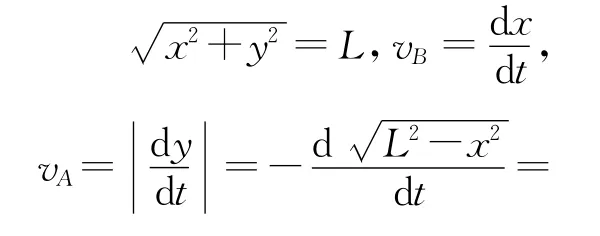
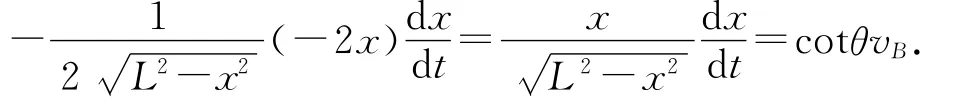
微分法变形AO=y=Lsinθ，BO=x=Lcosθ.以下通过对Lsinθ、Lcosθ对时间的微分将路程转化为速率.

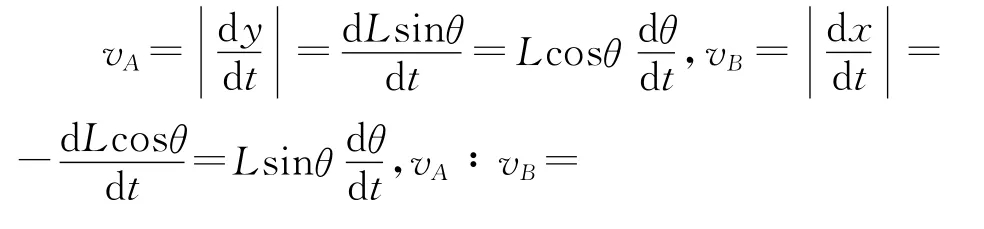
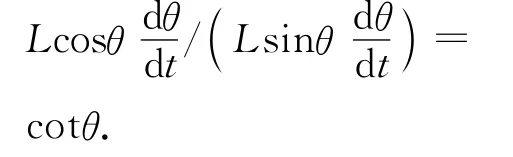
方法6：三角函数转化法.

如图7，木棒在极短时间Δt内，上端由A点滑落到A′点，下端由B点滑落到B′点.用极短时间Δt内在AA′和BB′的平均速度分别代替点A′和点B′的瞬时速度，可得

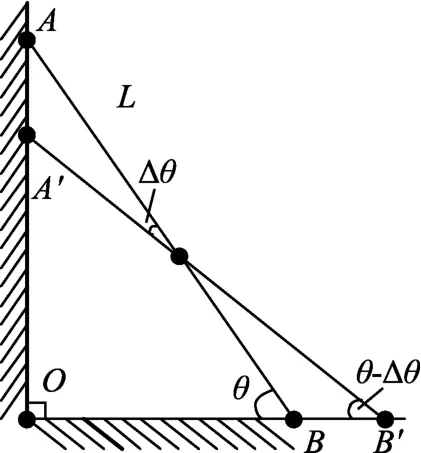
图7

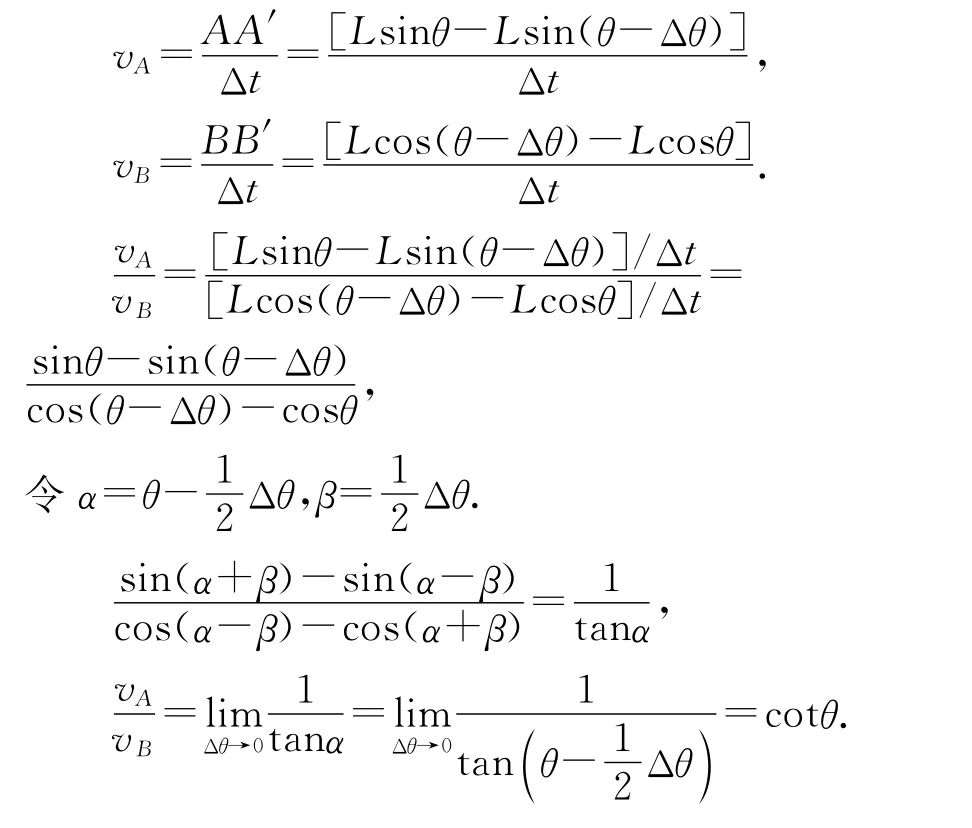
方法7：几何特征法.

当木棒沿墙壁自由下滑，由直角三角形斜边上的中线长度是斜边的一半可知：木棒中心的轨迹是一段圆弧（这是木棒运动的几何特征）.以O为圆心，L／2为半径画圆，交AB于O1，交A′B′于O2，则O1为木棒在AB位置的中心，O1Y1⊥AO交于Y1，O2Y2⊥AO交于Y2，O1X1⊥BO交于X1，O2X2⊥BO交于X2，O1X1⊥O2Y2交于O3，如图8所示.

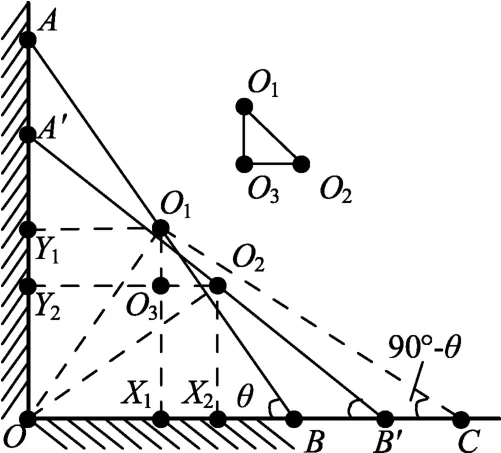
图8