正确认识动生电磁感应现象中的功能关系成立的参考系

闫来贵

（江苏省海安市曲塘中学，江苏 海安 226600）

1 问题的提出

功能关系是一条很重要的物理规律，即功是能量转化的量度.不同的功对应着不同形式的能量转化，如物体所受外力的总功是物体动能变化的量度，重力的功是物体重力势能变化的量度.

在物理教学和教辅资料中，关于动生电磁感应现象中的功能关系，一般总结为：导体棒做切割磁感线运动时，克服安培力做的功是其它形式的能转化为电能的量度，即电路获得的电功率等于导体棒克服安培力做功的功率.

对上述动生电磁感应现象中的功能关系，资料和文献一般在磁场不动、导体棒（单棒）运动的特殊情境下，给出了严格的证明.［1］所以，对于磁场不动、导体棒运动的情境下，此功能关系的正确性毋庸置疑，我们在分析相应的问题（磁场不动）时屡试不爽.

但文献［1-2］对2007年上海卷一道高考题的研究中指出：当磁场运动、导体棒也运动并做切割磁感线的情形下，此功能关系不再成立.笔者对文献［1-2］的这种观点持怀疑态度，即上述动生电磁感应现象中的功能关系，只在静止的稳恒磁场中做切割磁感线的导体棒成立，对运动磁场中做切割磁感线的导体真的不成立吗？

如何正确认识动生电磁感应现象中的功能关系及其成立的条件呢？

2 相关文献对动生电磁感应现象中的功能关系貌似不成立的高考真题研究回顾

例1.（2007年上海卷）如图1所示，光滑的平行长直金属导轨置于水平面内，间距为L、导轨左端接有阻值为R的电阻，质量为m的导体棒垂直跨接在导轨上.导轨和导体棒的电阻均不计，且接触良好.在导轨平面上有一矩形区域内存在着竖直向下的匀强磁场，磁感应强度大小为B.开始时，导体棒静止于磁场区域的右端，当磁场以速度v1匀速向右移动时，导体棒随之开始运动，同时受到水平向左、大小为f的恒定阻力，并很快达到稳定速度，此时导体棒仍处于磁场区域内.

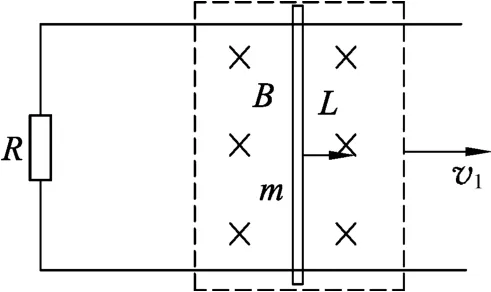
图1

（1）求导体棒所达到的恒定速度v2；

（2）为使导体棒能随磁场运动，阻力最大不能超过多少？

（3）导体棒以恒定速度运动时，单位时间内克服阻力所做的功和电路消耗的电功率各为多大？

2.1 关于第（3）问的解析

导体棒所达到的恒定速度大小和导体棒达到恒定速度v2后所受到的安培力大小分别为

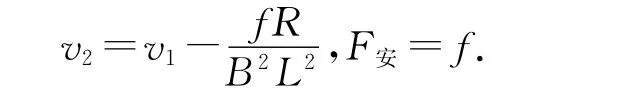
关于第（3）问，导体棒达到恒定速度v2后安培力做功功率、单位时间内克服阻力所做的功和电路消耗的电功率分别为［1-2］

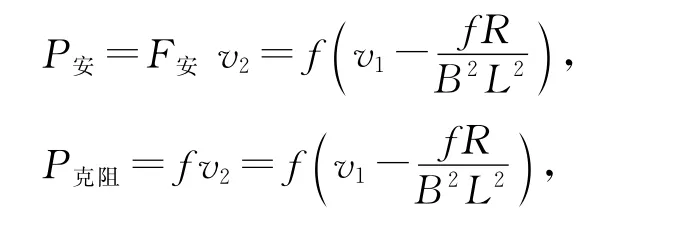
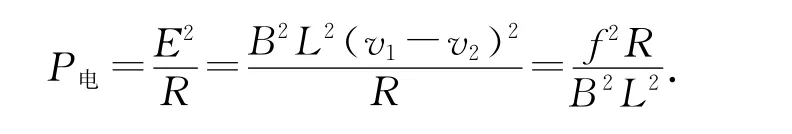
关于第（3）问，题目中没有特别指明参考系，一般默认是以地面为参考系的.因此，上述解析结果正确无误.

2.2 相关文献进一步分析时出现的困惑

文献［1-2］指出：在解这道题时，学生如果从功能关系出发，就会发现导体棒做匀速运动时，由于P安=P克阻，即安培力做的功等于克服阻力做的功，安培力做功消耗的能量转化为摩擦生热，根据功能关系电路中获得的电能从何而来呢？另外，在这道题中，由于P电≠P安，因此动生电磁感应现象中的功能关系“导体棒做切割磁感线运动以稳定速度运动时，电路获得的电功率等于导体棒克服安培力做功的功率”，在本题磁场运动的情境下不适合了.

2.3 相关文献对上述困惑的解释

文献［1-2］对上述困惑的解释：由牛顿第三定律，磁场受到等大的安培力（准确的说，应该是：与安培力等大的反作用力.笔者注），方向与磁场的运动方向相反，所以磁场克服安培力做功的功率为P克安=F安v1=fv1.从第（3）问解析中的几个表达式可以得出.即电路中所获得的电功率在数值上等于磁场克服安培力做功功率与安培力对棒做功功率之差.

可见，本题中动生电磁感应现象中的功能关系“导体棒做切割磁感线运动时，克服安培力做的功是其它形式的能转化为电能的量度，即电路获得的电功率等于导体棒克服安培力做功的功率”是不可靠的，它不具有普遍性.

3 如何正确认识动生电磁感应现象中的功能关系及其成立的条件呢

要正确认识动生电磁感应现象中的功能关系及其成立的条件，需要从产生动生电磁感应现象的微观本质（非静电力做功）中去理解，唯有如此才能真正看清此功能关系成立的条件是什么.

3.1 洛伦兹力的一个分力f 1对导体棒中所有电子做功的功率与电路消耗的电功率的关系

2007年上海高考题中，当导体棒达到恒定速度（是以地面为参考系的速度）v2时，导体棒相对于磁场静止的观察者为参考系，其速度大小为v相对=（v1-v2），方向向左，如图2所示.设导体棒中单位体积内的自由电子数为n，导体棒的长度和横截面积分别为L、S.

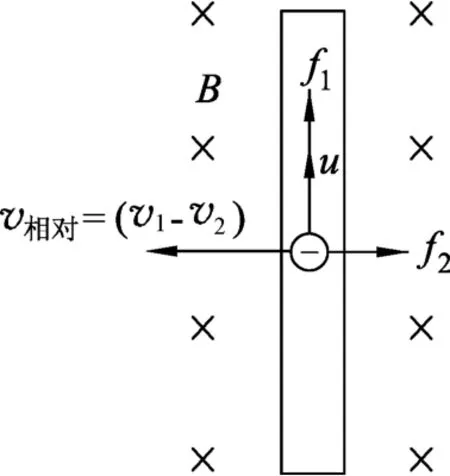
图2 微观分析

微观上，导体棒中的电子受到的洛伦兹力的一个分力沿棒向上，其大小为f1=e（v1-v2）B，［3］它是棒中产生动生电动势的非静电力，根据电动势定义，动生电动势为［4］

（4）式说明：微观上洛伦兹力的一个分力f1（非静电力）对导体棒中所有电子做功的功率P1，等于宏观上电路消耗的电功率P电=EI，也等于宏观上导体棒克服安培力做功的功率P克安=BILv相对=BIL（v1-v2）.需要注意的是：这里克服安培力做功的功率，是以相对于磁场静止的观察者为参考系的.

3.2 洛伦兹力的另一个分力f 2对导体棒中所有功电子做功的功率与安培力对导体棒做功的功率的关系

微观上，由于导体棒中电子的定向移动，电子受到向右的洛伦兹力f2=eu B，其对导体棒中所有电子做负功的功率为

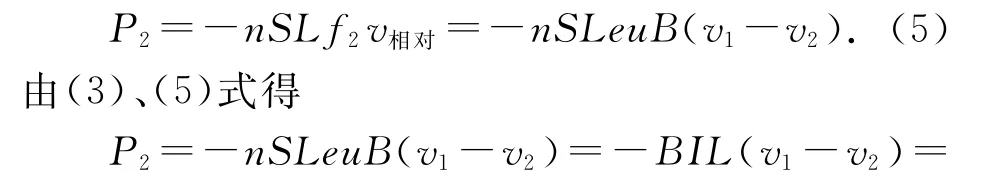
（6）式说明：微观上洛伦兹力的另一个分力f2对导体棒中所有电子做功的功率P2的绝对值，等于宏观上电路消耗的电功率P电=EI，也等于宏观上导体棒克服安培力做功的功率P克安=BILv相对=BIL（v1-v2）.仍需要注意的是：这里克服安培力做功的功率，是以相对于磁场静止的观察者为参考系的.

由（2）、（5）式可知：P1+P2=0，这表明：洛伦兹力的两个分力的总功率为0，即洛伦兹力永不做功，即电路中获得的电能并不是磁场本身提供的，而是磁场运动中克服安培力的反作用力需要其它外力对磁场做功，消耗其它形式的能量转化而来的，这与前面所述的文献［1-2］对困惑的解释一致.

综上所述，当磁场运动时，动生电磁感应现象中的功能关系“导体棒做切割磁感线运动时，克服安培力做的功是其它形式的能转化为电能的量度，即电路获得的电功率等于导体棒克服安培力做功的功率”也是成立的.

但需要特别注意的是：由于功具有相对性，功的计算与参考系有关.动生电磁感应现象中的功能关系中，克服安培力做的功（或功率）是以相对于磁场静止的观察者为参考系的.

即动生电磁感应现象中的功能关系成立的条件是：以相对于磁场静止的观察者为参考系的.

显然，文献［1-2］和部分师生产生困惑和错误认识的根源在于，对动生电磁感应现象中的功能关系成立的参考系是不清楚的，误认为是地面参考系了.