高阶椭圆型算子组广义低阶谱的估计式

黄振明

(苏州市职业大学 数理部，江苏 苏州 215104)

椭圆型偏微分方程是偏微分方程的一种类型，简称椭圆型方程.这类方程主要用来描述物理平衡稳定状态，如定常状态的电磁场、引力场、反应扩散现象等，其离散谱在实践中有着广泛应用.国内外学者的主要研究成果之一，就是得到了有关谱估计的几何或解析不等式[1-6].最近，笔者在文献[7]中探讨了如式(1)的四阶椭圆型算子组的谱问题，并得到了其主次谱估计不等式.

其中 Ω⊂Rm(m≥ 2)是1个边界逐片光滑的有界区域.

受此启发，笔者自然联想到，对于问题(1)的一般情形，即如式(2)的高阶椭圆型算子组的广义谱问题，是否还具有类似的谱估计不等式呢？

其中，整数l,t,h满足l≥2，t＞h≥1，i= 1,2,… ,l；ν是Ω边界∂Ω的单位外法向量；Δ=∇·∇为 Rm上的拉普拉斯算子；aij=aji是常数(i,j=1,2,… ,l)；A=（aij）l×l是正定矩阵，且对任意l维列向量ξ= (ξ1,ξ2,… ,ξl)T，满足

在式(3)中，v1,v2均为正实数；bij=bji是Ω→R上的非负函数(i,j= 1,2,… ,l)，且B=（bij）l×l是半正定矩阵.笔者依据微分算子谱的定性理论[8]，层层推导后发现，所提问题(2)的答案是肯定的，即其确实具有类似文献[7]中的谱估计不等式.

1 预备知识

为推导方便，记l维函数列向量u= (y1,y2,… ,yl)T，l阶算子矩阵Rp(f) =fpEl×l.其中，El×l为l阶单位矩阵；p为自然数；f为任一算子.那么，问题(1)可写成矩阵形式

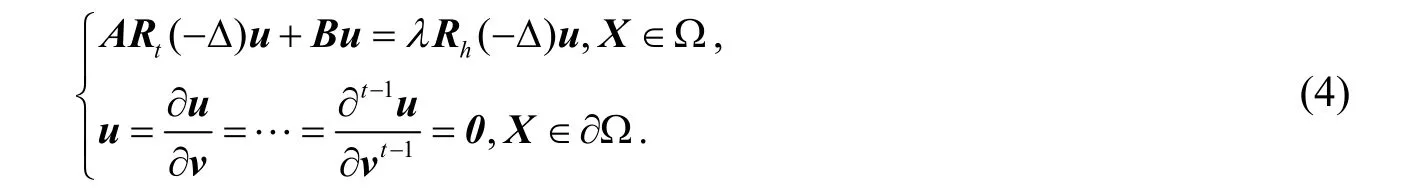
由于低阶谱在实际问题中表示了物体的主要特性，因此，本文仅讨论问题(4)的前2个谱，即主谱1λ和次谱2λ间的关系，记主特征向量为u，且满足规范化条件

利用问题(4)、式(5)、分部积分、式(3)和矩阵B的半正定性，有

即

另一方面，利用分部积分和kφ的定义，有

根据式(8)和式(9)，可得

再结合式(7)，可得

2 引理

引理1 设u是问题(4)中对应主谱1λ的主特征向量函数，则

证明：首先，用数学归纳法证明不等式

当i=h+1时，利用分部积分、Schwarz不等式和式(5)，有

此时，式(12)成立.

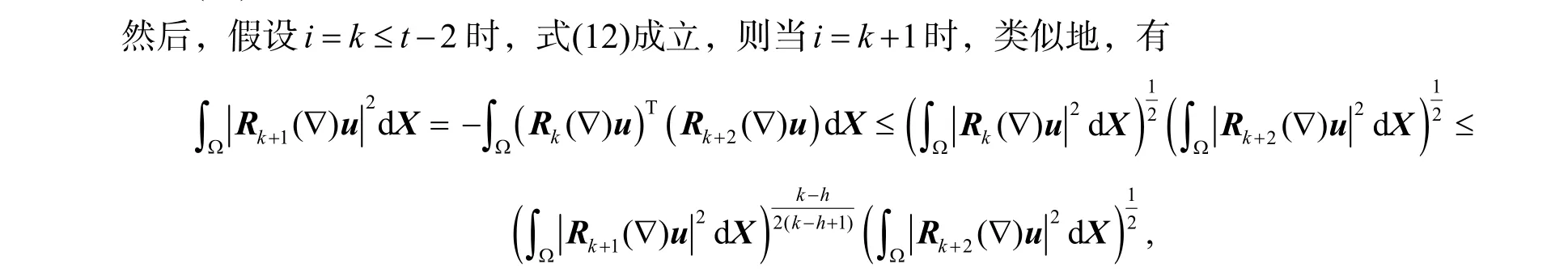
化简得

即i=k+1时，式(12)也成立.

最后，反复运用不等式(12)和式(6)，可得

引理1得证.

引理2 问题(4)的主谱1λ与其对应的特征向量u满足下列估计式：

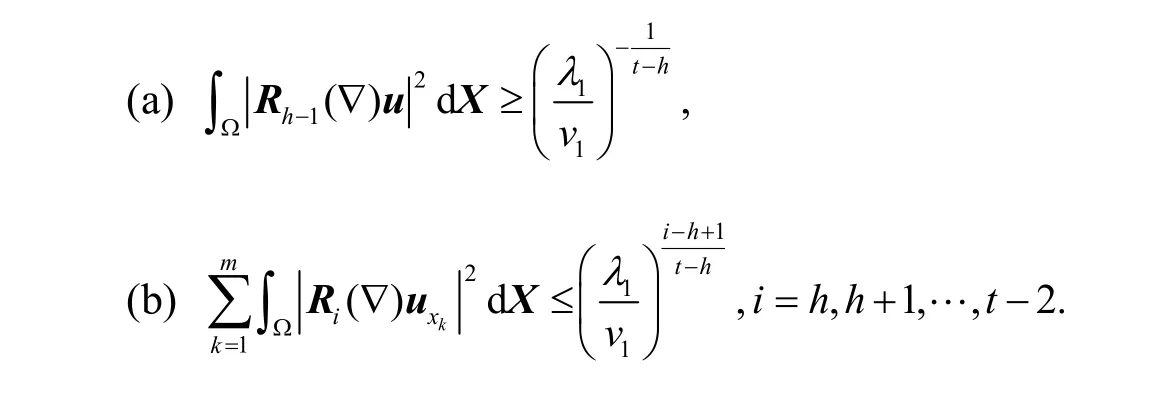
证明：(a) 利用式(5)、分部积分、Schwarz不等式和引理1，有

化简即得引理2(a).

(b) 类似地，利用分部积分、Δ的定义和引理1，有

引理2(b)得证.

引理3 对于L和M，分别有如下的上界估计：

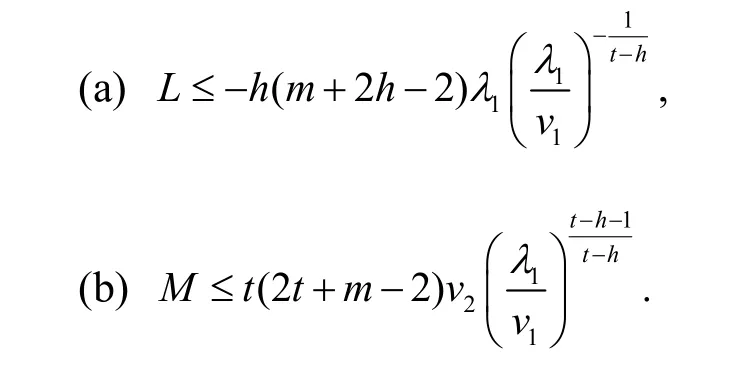
证明：(a) 利用kφ的定义和分部积分，有

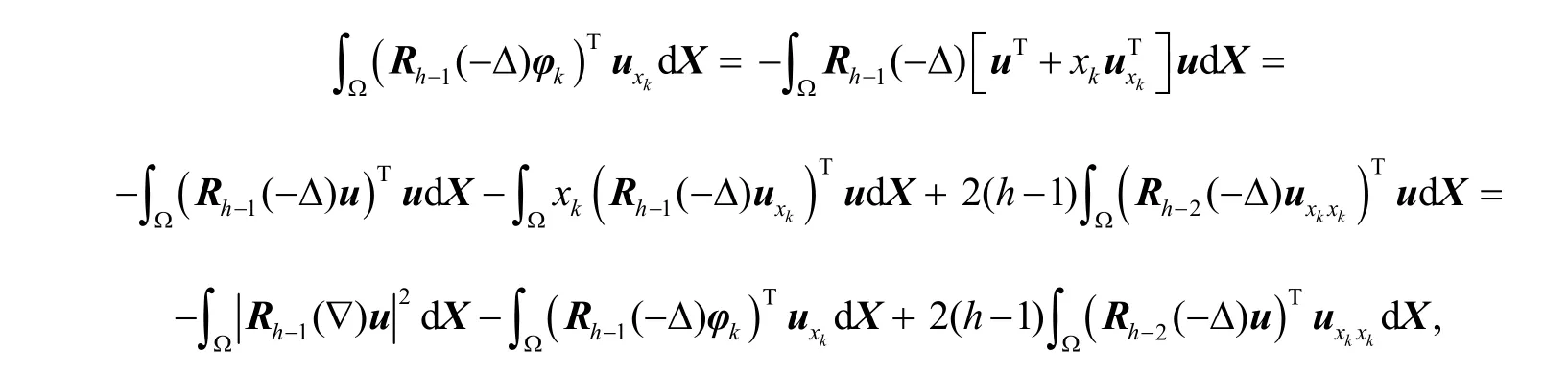
移项求和，得

再由L的定义和引理2(a)，可得

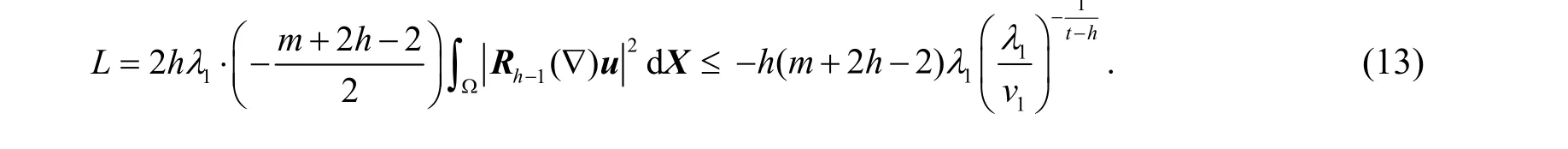
(b) 类似地，有

移项并利用分部积分，有

再利用式(3)、引理1和引理2(b)，有

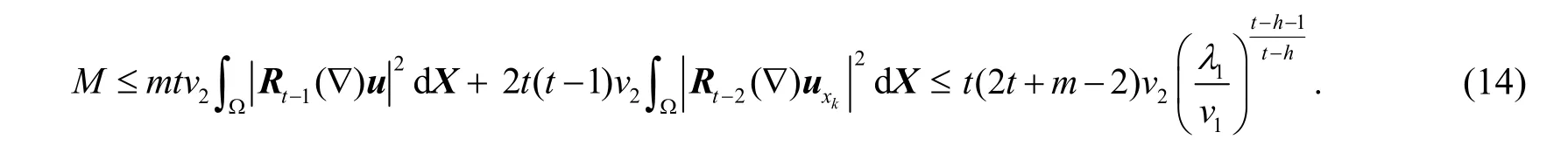
由式(13)～式(14)可知，引理3成立.

引理4 本文设定的测试函数组φk满足估计式

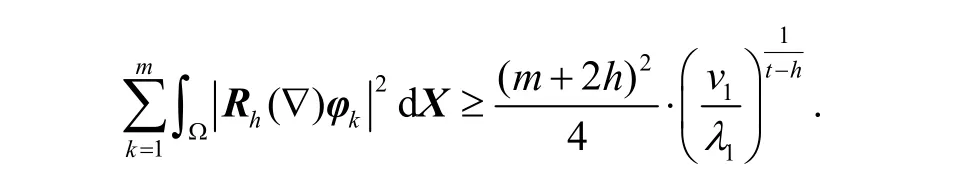
证明：利用函数组kφ的定义和分部积分，有移项可得

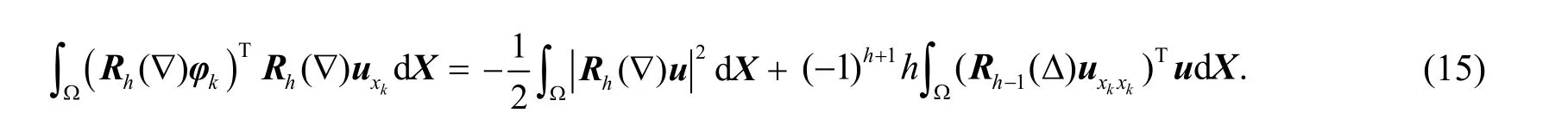
对公式(15)求和，并利用式(5)、Δ的定义和分部积分，有

对公式(16)运用Schwarz不等式，有

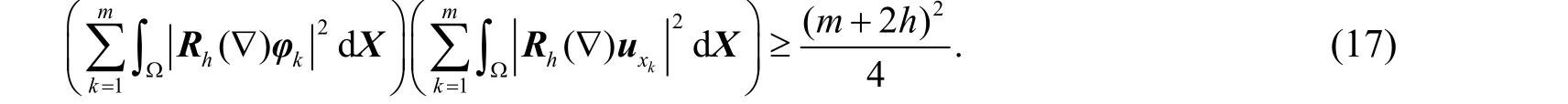
根据引理2(b)，式(17)左端第2项可表示为

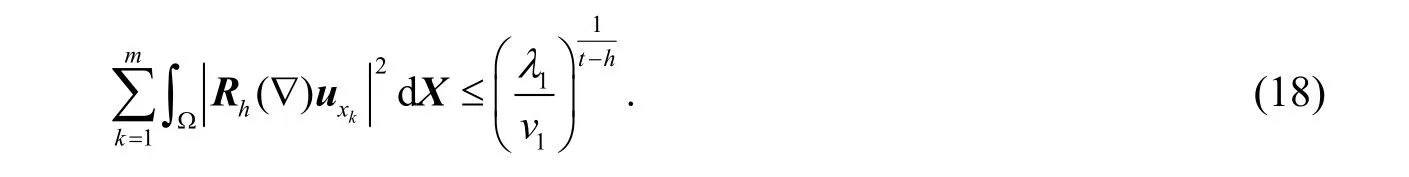
将式(18)代入式(17)，整理，引理4得证.

3 主要结果

定理 问题(4)的主次谱(1λ和 2λ)间隙满足估计式

证明：由式(11)得

将引理3～引理4的估计结论代入式(20)，化简整理即得定理中的式(19).

推论 问题(4)的主次谱之比存在估计下界

4 结语

在低阶椭圆型算子组的谱问题研究基础上，推广讨论了高阶椭圆型算子组的谱问题，根据算子谱理论，结合测试函数法，获得了前2个谱间的定量关系，所得结果拓展了参考文献[7]中的结论.