直抵知识内核落实数学思想

王荣香

【教学内容】

人教版三年级下册第七单元，第91页至92页例1，以及练习二十的第1题至第4题。

【教学目标】

1. 结合具体的情境认识小数，知道一位小数与十进分数的关系;借助小数单位认识小数，知道零点几就表示几个的0.1组成。

2. 在多元表征中经历小数的形成过程，在帮助学生建构就是0.的知识的同时体会单位的意义与价值，初步体会小数“满十进一”思想，发展学生的抽象思维及推理能力。

3. 在认识小数的过程中培养学生自主观察、思考辨析的能力，让学生在数学学习活动中体验探索的乐趣。

【教学重点】

让学生经历小数的形成过程，帮助他们建构就是0.的知识，体会单位的意义与价值，初步体会小数“满十进一”思想。

【教学难点】

经历从纯小数到混小数的认识过渡。

【教学过程】

一、在直观演示中体会单位意义，初步感知小数的“满十进一”思想

1. 情境导入，认、读小数。

出示教材第91页主题图，指导学生认、读小数，规范读、写法。

2. 实物表征，為“小数单位”留痕。

（1）认识0.1元。

课件出示1元人民币图。提问：这是1元人民币，你能通过它找到0.1元吗？（根据学生回答板书：1角=0.1元）

课件演示：1元换成10个1角。提问：1角是1元的几分之几？（根据学生回答板书：1角=（  ） 元

组织学生进行关系推理，得到（  ）  元=0.1元。

（2）认识0.1米。

①课件出示米尺图。提问：你能在这张米尺图上找到0.1米吗？（根据学生回答板书：1分米=0.1米）

课件演示：将1米平均分成10份。提问：1分米是1米的几分之几？（根据学生回答板书：1分米=（  ）米）

组织学生进行关系推理，得出：0.1米=（   ）米。

②认识不同位置上的0.1米。

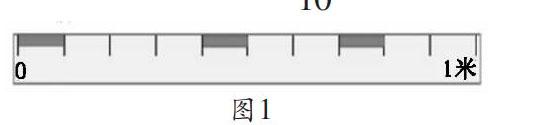
课件演示米尺图上第5小格、第8小格的长度（图1），提问：第5小格的长度用小数表示是多少？第8小格呢？学生回答后，追问：位置不同，为什么都表示0.1米？组织学生交流、思辨后小结：每一小格都是（ ）米，都是0.1米。

（3）认识0.（？摇？摇？摇？摇）米。

①课件演示：米尺图上3分米、6分米的长度。提问：3格的长度用分数和小数分别怎样表示？6格的长度呢？引导学生结合分数单位与小数单位进行描述。（教师板书：3分米=（ ）米，3分米=0.3米;6分米=（ ）米，6分米=0.6米）

再次组织学生进行关系推理，得出（ ）米=0.3米，（ ）米=0.6米。

②学生观察米尺图，在米尺图中找出其他用米作单位的分数和小数。根据学习经验，引导学生类比推理出：（ ）米=0.2米，（  ）米=0.4米……

追问：为什么2格的长度是0.2米？3格的长度是0.3米……教师要引导学生从计数单位累加的角度回答，归纳概括：0.（ ）米就表示有几个0.1米组成。

③提问：什么时候会是1米？让学生用自己的语言表述：0.9米再添上1个0.1米，是1米;10个0.1米合起来是1米。

二、在多元表征中体会单位的价值，理解小数的“满十进一”思想

1. 借计数单位，识小数本质。

①出示图2，组织学生观察、思考：用分数和小数表示各是多少？追问：形状不同，大小不一样，为什么都可以用0.3表示？

②出示一个空白正方形图。提问：怎样在正方形图中表示0.1、0.5、0.9？学生回答后追问：你有什么发现？

提问：把正方形平均分出的10份全部涂满，用哪个数表示？引导学生用小数单位累加的方式回答。

2. 借计数单位，认识比1大的小数。

①出示例1，提问：王东的身高是1米3分米，用小数表示是多少米？此问题可引导学生先思考3分米用小数表示是多少，再思考1米3分米用小数怎样表示。

②出示米尺图，提问：怎样在米尺图上表示1.3米？

③出示一个空白正方形图，提问：1.3米中的1.3这个小数，能用这一个正方形图表示吗？部分学生可能会说把正方形平均分成20份，涂其中的13份。这时可引导学生回忆找1.3米的方法，得出结论：1个正方形可以表示1，而1.3比1大，需要两个正方形。

④提问：用正方形图怎样表示2.5、3.2？学生回答后，课件演示。

3. 数形结合，认识数轴上的小数。

出示数轴，在数轴上找1.3、2.5、3.2的位置，让学生说一说是怎样找到的。

追问：想在数轴上找到9.9的位置，有什么好办法？学生可能从小数单位的角度回答，也可能基于“满十进一”思想回答。

三、在关联对比中体会单位的重要性，体会小数与整数中蕴含的思想

1. 课件动态演示：①逐步出示10个正方形，组织学生数正方形个数，从1个数到10个;②把1个正方形平均分成10份，组织学生数0.1，从一个0.1数到10个0.1。归纳总结：小数和整数一样都是“满十进一”。

2. 借助数轴，引导学生思考：在0～0.1之间还有没有小数？如果有，你认为要把这一小格再平均分成几份？

（作者单位：福建省大田县第二实验小学 责任编辑：王彬）