应用BP 神经网络和均值一次二阶矩法的连杆频率可靠性分析

胡启国，袁帅辉，王高爽

（1.重庆交通大学机电与车辆工程学院，重庆400074；2.重庆交通大学交通运输学院，重庆400074）

1 引言

可靠度是机械产品的重要指标，对机械产品的结构设计、强度寿命分析及选材方面有着重要的指导意义。自Birmbaum 首次提出可靠性分析的应力—强度干涉模型以来，现行的许多可靠性分析往往通过该模型配置一系列可靠性分析理论与方法求得机械系统或者零部件的可靠度[1]。例如，文献[2]通过对零部件上的负载响应过程进行极值分析，建立了极限载荷作用下的应力—强度干涉模型；文献[3]基于应力—强度边界理论建立了可同时处理泊松分布载荷的马尔科夫模型；文献[4]综合了应力—强度干涉理论和模糊集理论，研究了影响应力的外部载荷、材料属性、结构尺寸等参数为模糊设计变量时的可靠性求解方法，建立了模糊应力—随机强度可靠性分析模型；文献[5]针对应力—强度干涉模型表达式无法反映随机载荷作用次数对可靠度影响的问题，研究了随机载荷多次作用下的零件失效问题，建立了载荷多次作用下的零件可靠性模型。由应力—强度干涉模型，可将可靠度定义为造成失效的应力未超过抵抗失效的强度的概率，这里的应力和强度均为广义量，如温度、湿度等可以是导致失效的外部应力，而广义上的强度则表现为抵抗这种应力的抗力，如疲劳强度等[6]。但是文献[2-6]均以狭义上的载荷和静强度为目标，对传统应力强度干涉模型进行改进。为此，以某单缸发动机连杆为研究对象，应用多平台集成技术，研究了其工作频率和固有频率之间的关系，建立了共振失效下的频率失效功能函数，并结合均值一次二阶矩法有效地分析了连杆的频率可靠性，为机械零部件的可靠性分析及设计提供新的方法。

2 初选设计变量

连杆设计变量分布图，如图1 所示。设计变量中连杆大头和小头内孔尺寸CR2、CR9 与活塞销和曲柄销配合，CR1—CR14 均为形位尺寸。考虑到过渡圆角的改变会引起应力集中从而使连杆不满足静强度的设计要求，且在有限元分析前处理过程中往往对过渡圆角部分进行简化处理，故图1 所示的倒角圆尺寸CR13 取为定值；由静强度分析，需考虑一些对连杆结构及重量影响较大的参数，故在图1 所示的14 个设计变量中，选3 个定位尺寸CR3、CR6、CR12，三个几何尺寸CR1、CR8、CR14 以及材料性能参数：弹性模量E、材料密度DENS、屈服强度S 共9 个参数被初选为设计变量。

图1 连杆设计变量分布Fig.1 Design Variable Distribution of Connecting Rod

现已知连杆材料为20CrMo，假定以上变量均服从正态分布[7]，各线性尺寸设计变量的正态分布参数按GB/1084-2000 中有关未标注尺寸公差的V 要求进行设计；材料设计变量—密度DENS、弹性模量E 和屈服强度S 的变异系数均取0.1，各设计变量数值及分布特性，如表1 所示。

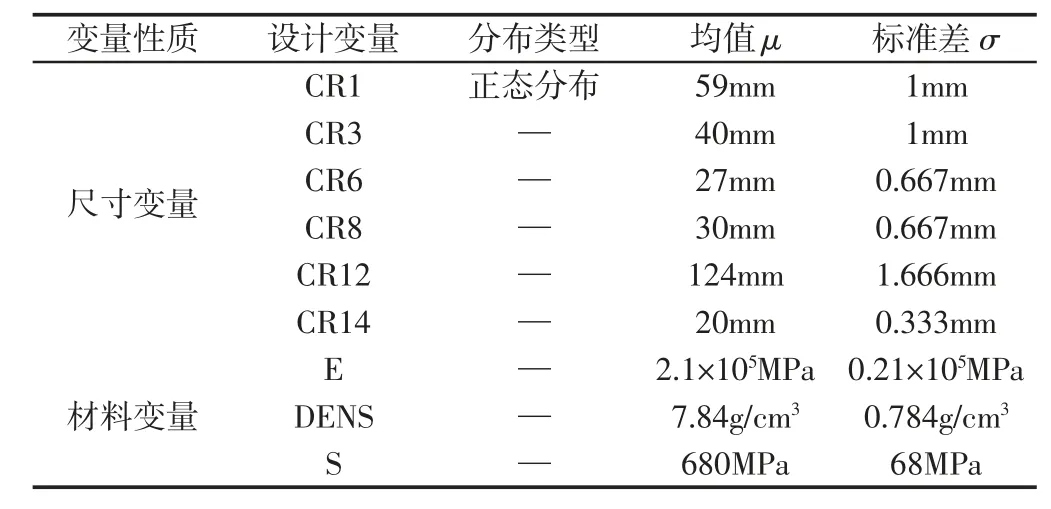
表1 设计变量的分布特性Tab.1 Distribution Characteristics of Design Variables

3 连杆模态分析及Isight 试验设计

3.1 连杆模态分析的运动方程

相比于刚度，连杆结构阻尼较小，可忽略其对固有频率和振型的影响。由达朗贝尔原理且当激振力为零时，在广义坐标X下，连杆的无阻尼自由振动微分方程为：

式中：A—振幅列阵，通过求解（2）式即可求得连杆的固有频率及振型。

3.2 基于ANSYS 的连杆模态分析

利用有限元分析软件ANSYS，结合表1 中设计变量完成连杆模型的建立以及网格划分。设置网格尺寸为3mm，得到最终的有限元分析模型，如图2 所示。该模型一共包含三层实体网格，共15997 个四面体单元。

图2 连杆有限元分析模型Fig.2 Finite Element Analysis Model of Connecting Rod

连杆属于平面运动且靠外力维持平衡，故接触边界上没有固定的自然约束，因此必须对其进行等效处理。连杆施加位移约束如下：在连杆对称面XOY 上施加对称约束，限制连杆的Z 向位移；在连杆对称面YOZ 上施加对称约束，限制连杆的X 向位移；同时为消除分析模型的刚体移动，在远离结构重要分析部位（连杆大头对称面所处的一系列节点）对连杆施加Y 向位移约束。

连杆所做多自由度振动可以看作各阶振型的线性叠加，而连杆的振动特性主要取决于低阶振型。振动系统的低阶模态相比高阶模态占有的权重更大，采用Block Lanczos 模态提取法，得到连杆前四阶固有频率及振型。四冲程发动机运转时其工作频率与转速存在如下换算关系：

式中：n—发动机对应的工作转速；z—气缸数量，f 由转速换算得来的振动频率，由于所研究的为单缸内燃机发动机连杆，故z=1。由式（3）知，连杆前4 阶固有频率、振型及对应等效临界转速，如表2 所示。

由表2 可知，连杆最小临界转速10807r/min 是由最低阶固有频率计算而得的临界转速。NC450 型单缸发动机的稳定工况转速为9000r/min，理论上没有发生共振的可能性。但在实际制造过程中，尺寸变量和材料变量成随机性变动，引起连杆最低阶固有频率波动，使得连杆稳定工况转速与最小临界转速重合，连杆发生共振失效的概率增大，因此有必要对连杆的频率可靠度进行计算。

表2 连杆前4 阶固有频率、振型及临界转速Tab.2 The First Four Order Natural Frequency，Vibration Modes and Critical Rotary Speeds of the Connecting Rod

3.3 ANSYS 集成Isight 联合仿真

利用Isight 软件中集成ANSYS 的组件，设计连杆模态联合仿真，通过修改集成计算模块的输入文件来完成分析模型的修改，从而快速得到随机输入下的响应值。

将表1 中的9 个初选设计变量作为频率可靠性分析的随机变量，采用拉丁超立方抽样（LHS）采样方法获得联合仿真所需的设计变量样本；通过Isight 和ANSYS 集成时的调用程序，进行相应的随机有限元分析和计算。采样获得的连杆随机设计变量及相应的最低阶固有频率的样本值，如表3 所示。

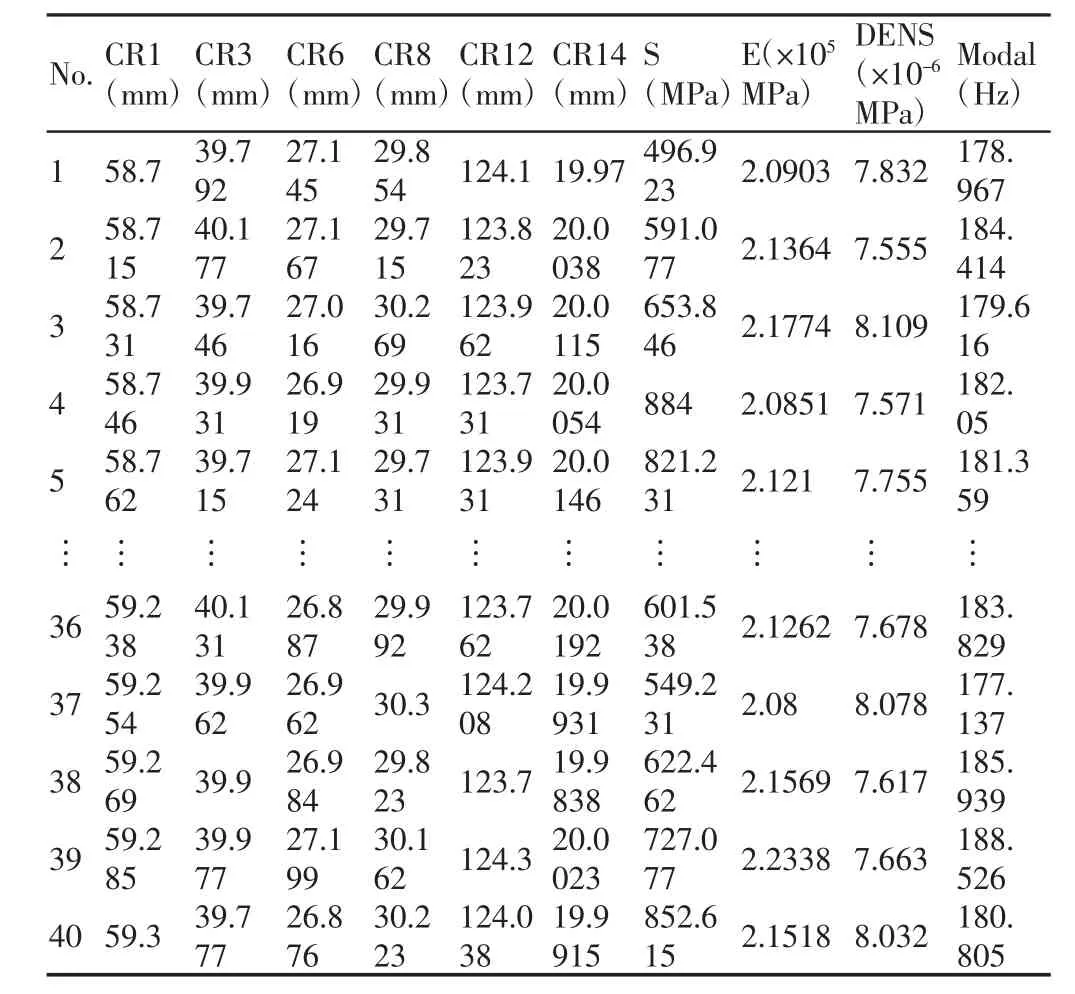
表3 设计变量及最低阶固有频率样本点值Tab.3 Design Variables and Minimum Order Natural Frequency Sample Points

3.4 DOE 样本分析

频率失效功能函数拟合时，过多的设计变量会影响曲线的拟合精度。利用Isight 软件集成ANSYS，对表3 中的初选变量进行DOE 实验设计，分析得到各初选设计变量的Pareto 贡献率图3（a），以及各设计变量交互效应Pareto 贡献率图3（b），图中蓝色表示正效应，红色表示负效应。如图3（a）所示，经DOE 样本分析，连杆最低阶固有频率的敏感设计变量为：连杆大头外圆直径CR1、连杆大小头中心距CR12、连杆材料弹性模量E 以及连杆材料密度DENS。由图中颜色判断设计变量CR1 和E 对最低阶固有频率为正相关，而设计变量DENS 和CR12 对连杆最低阶固有频率为负相关。特别地，由材料力学知识，弹性模量E 和材料密度DENS 存在相关性，但由图3（b）知，E 和DENS 的相关性对最低阶固有频率的响应几乎为零，因此可以把弹性模量E 和密度DENS 视为两个独立的设计变量。

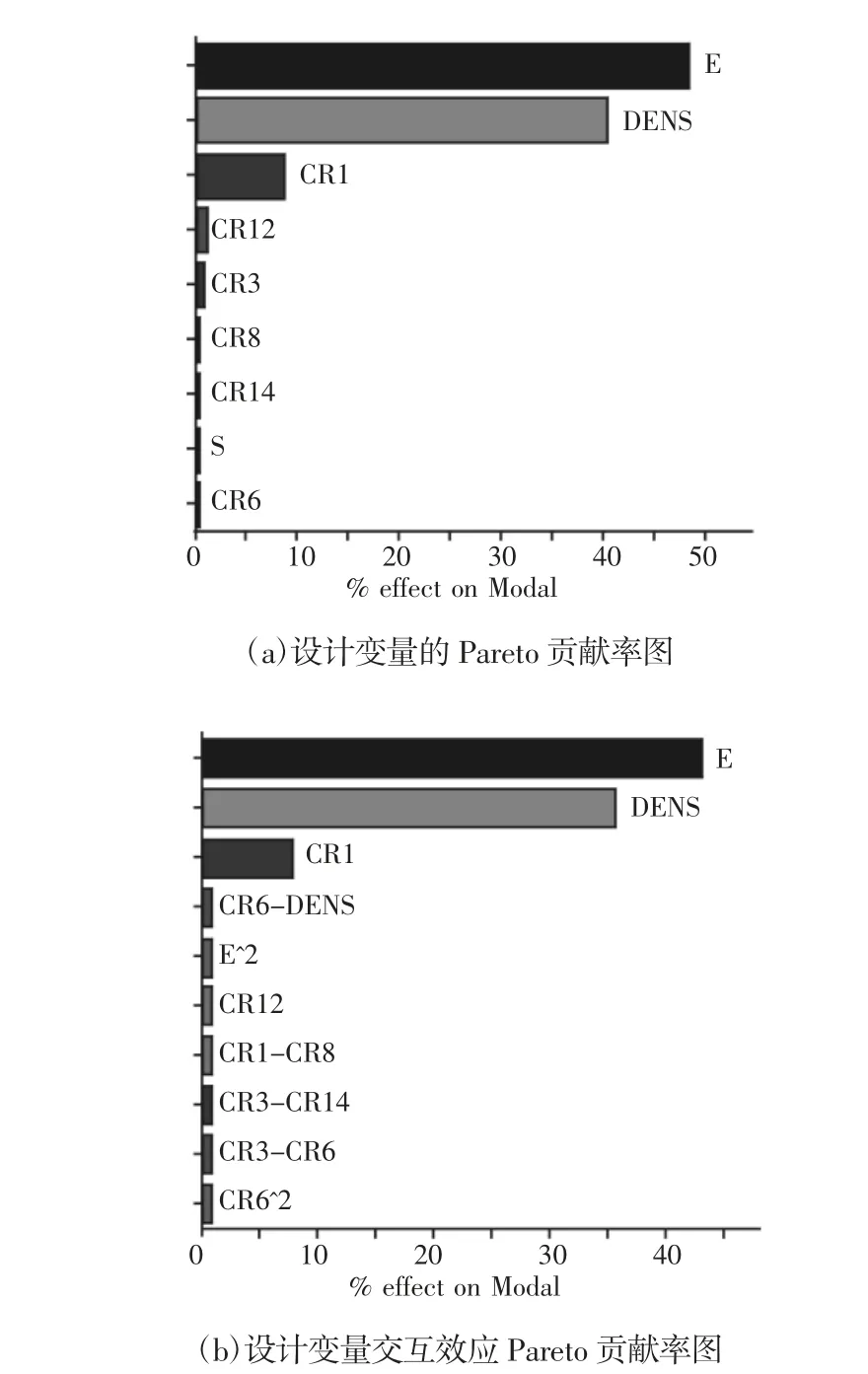
图3 设计变量的Pareto 分析图Fig.3 Pareto Analysis Diagram of Design Variables

4 非线性神经网络回归分析

采用Matlab 编程的方法，利用BP 神经网络拟合连杆最低阶固有频率与设计变量之间的函数关系。输入层参数为3.4 节分析得到的4 个敏感设计变量，输出层参数为连杆最低阶固有频率。通常，单隐含层结构的神经网络足以以任意精度逼近所要拟合函数[8]，故采用单隐含层BP 神经网络，其输入层神经元个数为4，输出层神经元个数为1。隐含层的节点数可按以下经验公式进行选择：

式中：l—隐含层神经元个数；m—输入层神经元个数；n—输出层神经元个数；a—（1～10）之间的整数。

由式（4）可知隐含层神经元个数l 介于（3～12）之间，由试凑法进行多次拟合实验，以达到提高拟合精度、缩短样本训练时间、避免出现过拟合等目的，最终确定隐含层神经元个数为5，建立如图4 所示的BP 神经网络。

令［CR1，CR12，E，DENS］T=［x1，x2，x3，x4］T，由图4 并参考文献[9]知，连杆最低阶固有频率Y 与随机变量X 之间的拟合函数表达式为：

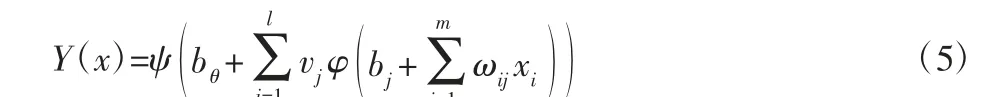
式中：ωij—输入层到隐含层的网络连接权值；vi—隐含层到输出层的网络连接权值；bj—隐含层的阈值；bθ—输出层阈值；φ（·）—隐含层传递函数；ψ（·）—输出层传递函数。设置输入层到隐含层的传递函数为“logsig”（对数S 型传递函数），隐含层到输出层的传递函数为“purelin”（线性传递函数）。

图4 BP 神经网络结构图Fig.4 BP Neural Network Structure Diagram

设定网络训练的目标误差为10-1，训练次数为1000 次，对表3 数据进行学习训练。经训练，符合精度要求的样本真实值和预测值的对比图及训练误差分布图，如图5、图6 所示。

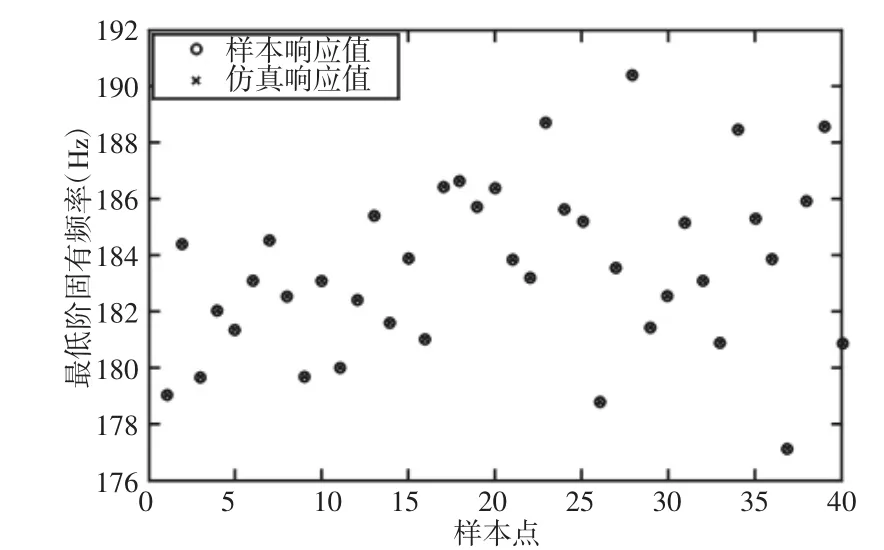
图5 样本响应值与仿真值比较Fig.5 Comparison of Sample Values and Simulation Values

由图5 和图6 可知，训练后的误差在0.1 以内，网络实际输出值接近期望输出值，网络拟合效果较理想，训练出的函数拟合精度较高。因此，该拟合函数可用来构建连杆频率失效功能函数，完成连杆的频率可靠性分析。

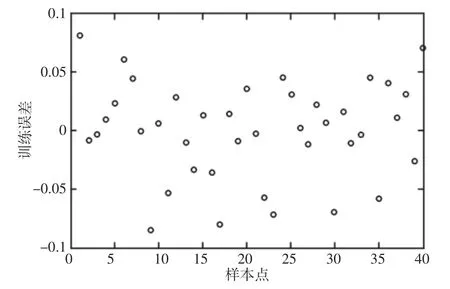
图6 神经网络训练误差分布图Fig.6 Neural Network Training Error Distribution

5 连杆频率可靠性分析

由可靠性基本理论，结构失效功能函数G（X）的表达式如下：

式中：X=（x1，x2，…xn）—相互独立的设计变量；n—随机设计变量的数目，且n=4。当G（X）＞0 时结构安全可靠，G（X）＜0 时结构失效，G（X）=0 时结构处于极限状态。通常情况下，功能函数可定义为响应量和阈值的差[10]，即：

式中：y（X）—最低阶固有频率的响应量，对应于式（5）所示的最低阶固有频率响应函数；y*—阈值，对应于发动机相应工况转速的换算频率值。

现已知NC450 型发动机连杆的最大扭矩转速为7000r/min，最大功率转速为9000r/min，极限转速为11000r/min。显然，发动机极限转速与表2 中的最低阶固有频率对应的临界转速最为接近，此时连杆发生失效的可能性最大。但发动机在极限转速下工作的频次近乎为零，因而不能选做对应阈值工况。由于连杆设计变量的随机性变动使得其最低阶固有频率值呈现随机性，最小临界转速落入最大扭矩转速与最大功率转速区间的概率加大，即（7000～9000）r/min 之间，较之最大扭矩工况7000r/min，连杆在最大功率工况9000r/min 下的失效概率大，且最大功率工况为发动机常用稳定工况，因而选取最大稳定工况对应的转速对应的频率值为阈值y*，由（3）式求得y*=150HZ。

综上述，结合式（5）和式（7）知，最大稳定工况下连杆频率失效功能函数如下：

式（8）所示的频率失效功能函数为非线性函数，由可靠性分析的非线性功能函数的均值一次二阶矩法[11]，可靠性指标β 及可靠度R 计算如下：

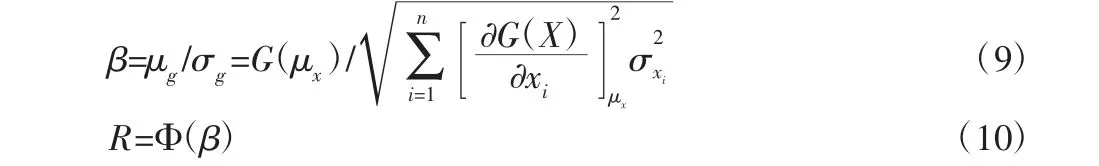
式中：n—设计变量的个数；μx—随机变量X 的均值向量；σxi—参数xi的标准差。由式（9）和表1 中相应设计变量的分布特征，求得频率可靠度指标β=3.14，进而求得连杆的频率可靠度为R=0.9992，为连杆结构参数和最低阶固有频率值得优化提供了依据。

6 结论

以频率可靠性为研究对象，采用多平台集成设计方法，结合神经网络回归分析以及机械结构可靠性分析方法，以NC450 型单缸发动机连杆为例，详细介绍了频率可靠性分析方法。

（1）与传统可靠性分析方法不同，借助Isight 设计DOE 样本分析实验，在可靠性分析之前（失效功能函数拟合前）对各设计变量进行可靠性灵敏度分析，提升了频率失效功能函数的拟合精度；

（2）根据DOE 样本分析，确定了各随机变量对连杆频率可靠度敏感程度，其中，影响较大的设计变量为连杆大头外圆直径、连杆大小头中心距、连杆材料弹性模量、连杆材料密度，对连杆的可靠性优化设计具有一定的指导意义；

（3）将Isight 与ANSYS 集成设计模态联合仿真，得到了连杆随机设计变量下的最低阶固有频率响应样本值。由BP 神经网络拟合相应的函数关系，建立了频率失效功能函数，并利用一次二阶矩法完成连杆的频率可靠度求解，为机械零部件的可靠性分析提供了新的研究思路。