基于VMD-SWT 联合算法的谐波/间谐波检测

付 华，刘 超，张 松

（1.辽宁工程技术大学电气与控制工程学院，葫芦岛 125105；2.唐山三友集团，唐山 063000）

随着风电、光伏等新能源发电和电力电子技术在电力系统中的广泛应用，电网中的谐波问题越来越复杂[1]，整数次和非整数次谐波、稳态和暂态谐波同时存在，不仅会增加设备损耗、降低计量设备的精度和稳定性，还会造成电网电压波动和闪变，因此，谐波/间谐波信号的快速准确检测对于谐波治理具有重要意义。

针对电网中存在的谐波和间谐波，传统的检测方法有傅里叶变换[2]、小波变换[3]和希尔伯特-黄变换HHT（Hilbert-Huang transform）[4]等。傅里叶变换检测整数次谐波具有较高精度，但是对于暂态谐波和间谐波等非平稳信号，无法避免因非同步采样引起的频率泄露和栅栏效应。小波变换具有良好的局部性特征，但需要人为选择小波基和分解层数，选择不同，检测结果差别可能会很大，且会存在频带混叠。HHT 作为一种自适应算法，不受基底和分解层数影响，完全由数据驱动，对稳态和暂态谐波均具备分析能力，但是在经验模态分解EMD（empirical mode decomposition）分解时容易出现欠包络和过包络[5]，对于含噪信号或者频率相近的谐波信号会产生模态混叠，此时会得到错误的HHT 检测结果，甚至产生无法解释的负频率。

近期，Dragomiretskiy 等[6]提出了一种新的完全非递归的模态变分方法，即变分模态分解VMD（variational mode decomposition）。不同于EMD 使用的循环筛分剥离方法，VMD 通过在变分框架内迭代寻找变分模型最优解的方式确定带宽和中心频率，其实质是用维纳滤波估计模态残留[7-8]，因此具有较强的抗噪能力，已被成功应用于变压器故障诊断[9-10]、高压输电线路雷击故障测距[8]、旋转机械故障诊断[11]等领域。虽然VMD 不具有递归模态分解的缺点，但需要预先判断原始信号中分量个数，这使得该方法的计算效率较低且自适应性不高。对VMD 分解得到的模态分量还需要有效的时频分析工具处理，Daubechies 等[12]提出的同步挤压小波变换SWT（synchrosqueezing wavelet transform）将小波变换后的时频图在频率域方向进行压缩，获得较高频率精度的时频曲线，且各时频曲线间不存在交叉项[13]，已被应用在气候分析[14]、机械故障诊断[15]、信号消噪[16]、土木工程结构[17]、地震信号提取[18]中，且效果良好。

本文将变分模态分解结合同步挤压小波变换引入到谐波治理中，提出一种谐波/间谐波检测的新方法。利用VMD 弥补SWT 变换对相近频率分离不彻底的不足，利用SWT 预判分量个数、锐化时频曲线，结合二者噪声鲁棒性上的优势，实现较高精度的谐波检测和参数识别。

1 谐波信号变分模态分解

将含有谐波/间谐波的电力信号s（t）分解为K 个具有稀疏属性的模态，每个模态围绕着一个中心频率，则变分模态分解具体分为构建和求解两个阶段。

1.1 谐波信号变分问题的构建

计算第k 个模态uk（t）的解析信号，其单边频谱为

式中，δ（t）为单位脉冲信号。

对单边频谱进行指数修正调整预估的中心频率wk，使其移动到基带上，即

式中：uk（t）=Ak（t）cos（φk（t）），Ak（t）和φk（t）分别为模态uk（t）的瞬时幅值和相位；wk为第k 个模态的中心频率，wk=φk'（t）=dφk（t）/dt。

采用解析信号的H1高斯平滑估量各模态带宽，保证带宽之和最小，得到变分模型为

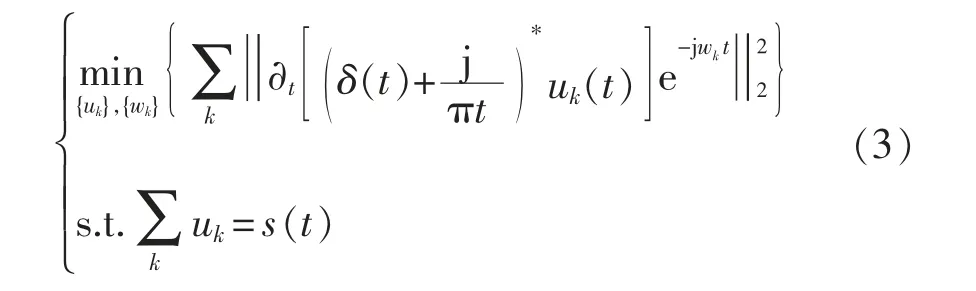
1.2 变分问题的迭代优化求解

引入Lagrange 乘子λ（t）和二次惩罚因子α 构建非约束拉格朗日表达式，即

其中λ（t）起到约束不等式的作用，α 保证噪声条件下的数据保真。

使用交替方向乘子算法ADMM（alternating direction method of multipliers）不断更新优化λn+1，n 代表迭代次数，寻找增广式（4）的鞍点即变分模型最优解，迭代过程为

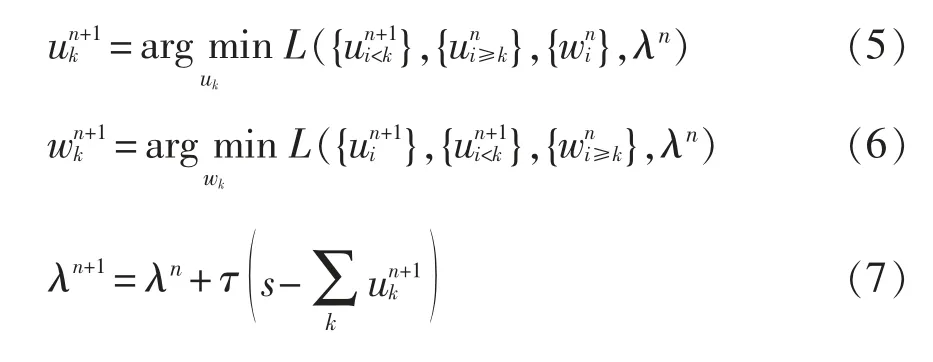
ADMM 二次优化求解得

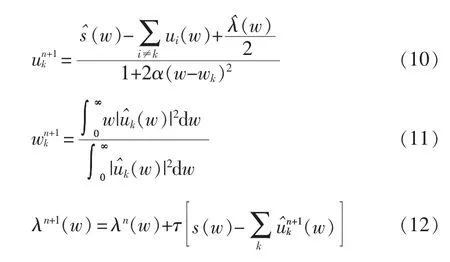
式中，带“^”标符号表示原符号变量的傅里叶变换。

迭代值更新过程中，要满足收敛条件

2 谐波信号参数估计和挤压重构

SWT 以连续小波变换CWT（continuous wavelet transform）为基础[19]，对中心频率附近的小波系数重组挤压，改善尺度方向的模糊现象，提高时频分析精度。本文通过SWT 实现谐波/间谐波信号的参数识别，具体如下。

2.1 瞬时频率估计

对s（t）进行时域CWT，得到小波系数为

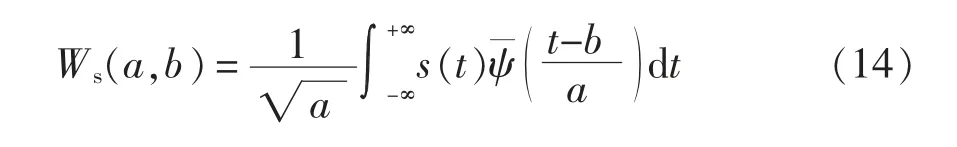
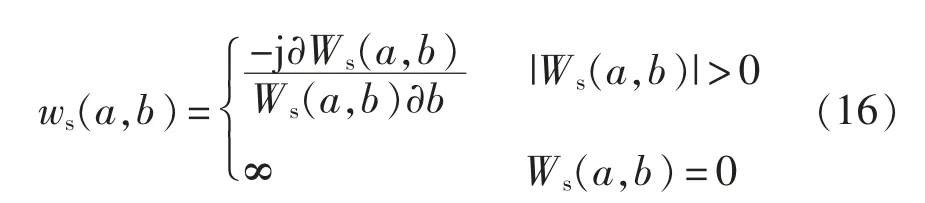
2.2 挤压锐化和重构

在按照能量大小重新排列和挤压过程中，中心频率附近的小波系数被压缩在频率wl附近，则在区间[上的同步挤压变换量值为

式中：Δw=wl-wl-1，l=0，1，2，…，na-1，na=Lnv，L 与s（t）的信号长度n 有关（n=2L＋1），nv=32；Δai=ai-ai-1；ai为离散尺度。

由式（17），SWT 把时间-尺度平面[b，Ws（a，b）]重新转换到时间-频率平面[b，wl]，利用同步挤压反变换重建信号得

3 VMD-SWT 联合算法的谐波/间谐波检测

VMD-SWT 联合算法对谐波/间谐波提取和检测步骤如下。

步骤1对含有谐波/间谐波的电力信号s（t）按式（14）进行连续小波变换得到小波量图，根据时频图分布情况确定模态分量个数K，并对式（16）离散化得到。

步骤2设置参数K、α 和τ 等。其中α 值会直接影响到分解结果，α 越小，分解得到的模态带宽越大，反之带宽越小，经实验发现，α 在1 500～3 000 范围内取值分解效果较好。τ 表示耐噪声程度，τ 越小，噪声耐受越强，故取0 或较小值较合适。因此，α 取值2 000，τ 取值0，K 则根据步骤1 确定。

步骤3对s（t）进行VMD 分解成K 个模态分量，即

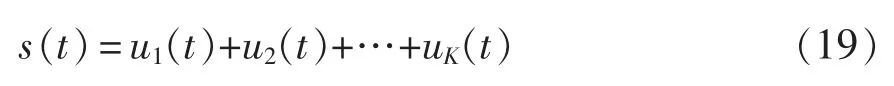
步骤4对模态uk（t）的小波系数进行去噪和同步挤压，中心频率wl附近同步挤压变换为

式中，wl=w02lΔw，其中：Δw=lb（n/2）/（na-1），w0=1/（nΔt），Δt 为采样时间间隔，则可以划分成不同频率的区间[（wl-1+wl）/2，（wl+wl+1）/2]，并在区间范围内锐化时频曲线，使各曲线间不存在交叉项。

步骤5重组压缩后，小波脊线得到充分去噪和细化，有利于提高参数识别精度，选取相平面上满足ts（b，a）=b 的所有（b，ar（b））点构成小波脊线ar（b），则瞬时频率和幅值分别为

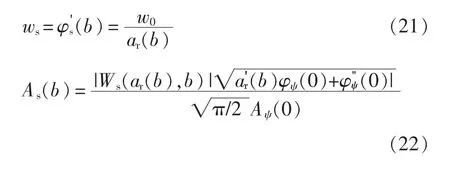
4 算例和实例分析

4.1 算例1

设稳态谐波信号为

信号的采样频率为4 096 Hz，采样时间为1 s。原始信号中除了谐波处还存在与3 次谐波频率接近的110 Hz 间谐波，在含噪30 dB 条件下，对信号进行VMD 分解，但模态分量个数无法明确预知，若一一取值实验，不仅降低了运算效率，而且选取不当会造成结果错误，因此本文提出对信号进行连续小波变换来预估K 值，母小波函数具有快速衰减性，对应的傅里叶变换在负频率域趋近于0，相同频率集中分布，通过式（16）初步估计瞬时频率得到小波量图，如图1 所示。由图1 可见，存在5 条清晰且连续的时频曲线，每条曲线集中在一个频率处对应着不同的模态，故可判断信号分量个数为5。以此为据进行VMD 分解（K=5）得到IMFs，如图2 所示，为方便观察分析，仅展示2 000 点。

图1 算例1 稳态谐波信号小波量图Fig.1 Wavelet map of steady-state harmonic signal in case 1

由图2 可知，VMD 将加噪信号分解成5 个模态，每个模态均为单一频率波，不存在模态混叠现象，实现了各谐波模态的有效提取。对IMF 分量进行SWT 小波脊线识别瞬时频率和幅值，结果如图3和图4 所示。

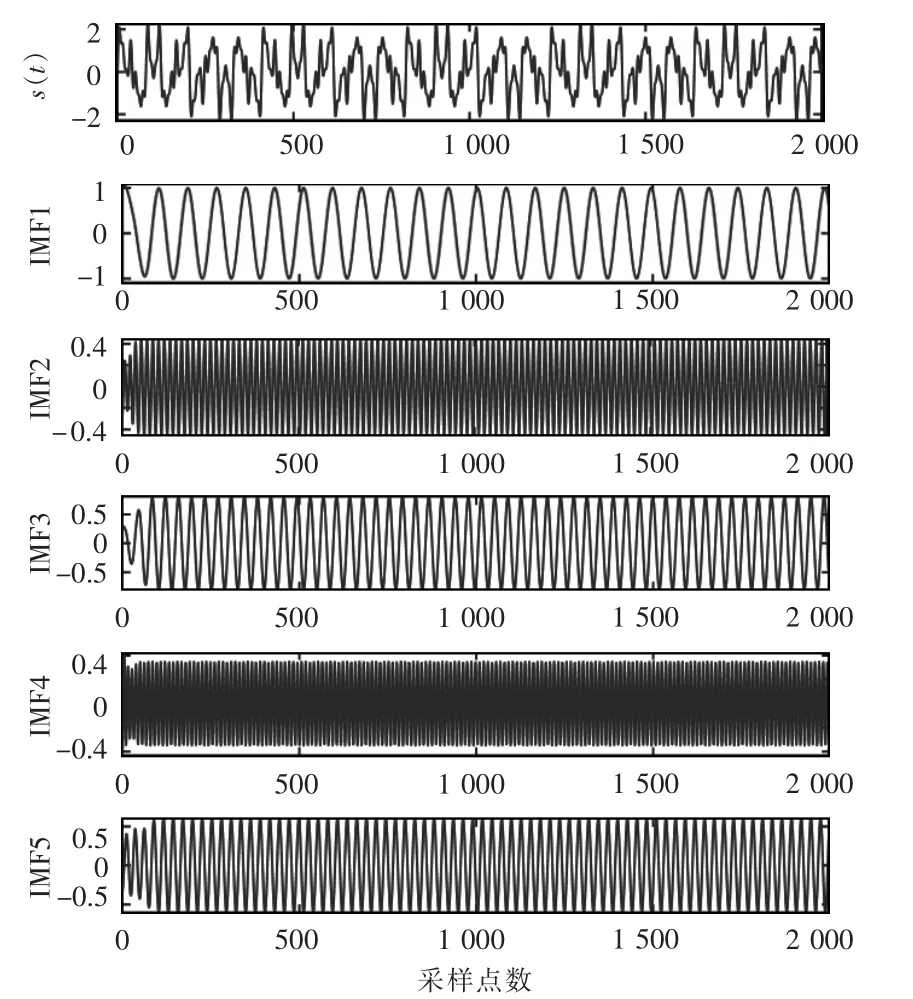
图2 算例1 VMD 分解结果Fig.2 Decomposition results based on VMD in case 1

由图3 和图4 可见，各IMF 的瞬时频率和幅值检测结果与理论值较为接近，除去两端部分基本保持一条直线，波动较小，表1 给出了SWT 小波脊线参数识别结果。

图3 算例1 的IMF 分量瞬时频率Fig.3 Instantaneous frequency of IMF components in case 1

图4 算例1 的IMF 分量瞬时幅值Fig.4 Instantaneous amplitude of IMF components in case 1

表1 数据表明在含噪30 dB 时，幅值检测的误差平均为0，频率检测的平均误差为0.571%，对稳态谐波具有较高的检测精度，同时说明在去掉两端波动值后取平均值可以有效提高参数的识别精度。

表1 算例1 的VMD-SWT 参数识别结果Tab.1 Parameter identification results based on VMD-SWT in case 1

4.2 算例2

设暂态时变谐波/间谐波信号为

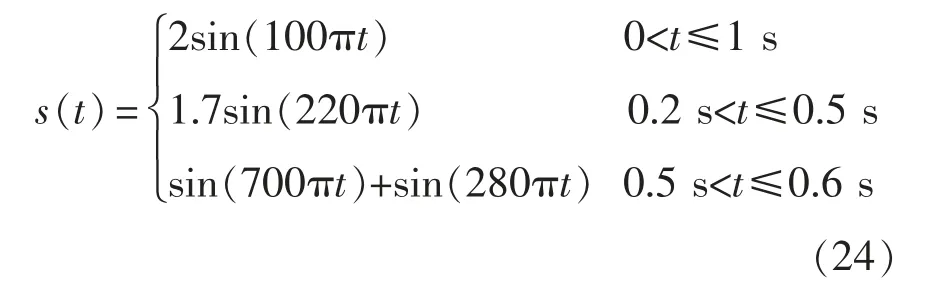
信号的采样频率和采样时间同算例1，4 096 个采样点内基波一直存在，采样点819.2～2 048 处是幅值为1.7，频率为110 Hz 的间谐波，采样点2 048～2 457.6 处同时存在7 次谐波和频率为140 Hz 的间谐波。在20 dB 噪声环境下，对信号进行CWT，获得小波量图如图5 所示。可见图5 中有3 条清晰且连续的曲线，因此令K=3，对信号进行VMD 分解，得到IMFs 分量，如图6 所示。

图5 算例2 暂态谐波信号小波量图Fig.5 Wavelet map of transient harmonics signal in case 2

从图6可见，VMD 分解得到的前2 个模态分量分别对应着基波和7 次谐波，IMF3 准确地提取出间谐波分量，表明VMD 分解不仅可以分离稳态信号，对暂态信号也具有良好的提取效果。篇幅限制，只给出IMF3 分量进行SWT 小波脊线检测的瞬时频率和幅值，如图7所示。由图7 可知，IMF3 发生和恢复的时刻定位比较准确，导出采样点[819，2 048]和[2 048，2 458]对应时间段的各参数，并计算其平均值，结果如表2 所示。

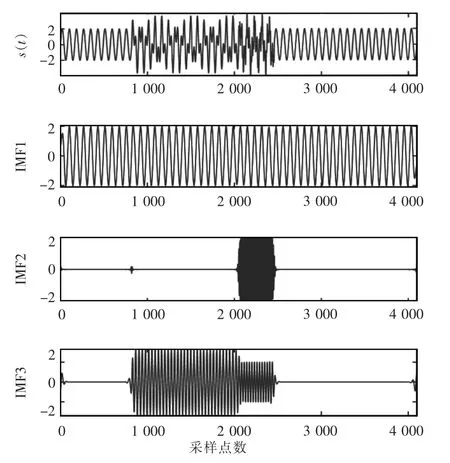
图6 算例2 VMD 分解结果Fig.6 Decomposition results obtained using VMD in case 2

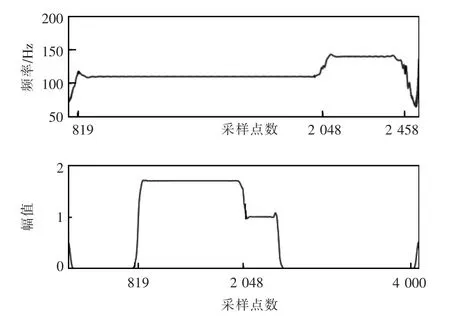
图7 IMF3 分量的SWT 识别结果Fig.7 SWT identification result of IMF3 component

表2 数据表明，在20 dB 噪声环境下，频率检测的平均误差为0.648%，幅值的平均误差为1.577%，检测结果比较接近理论值，精度较高。

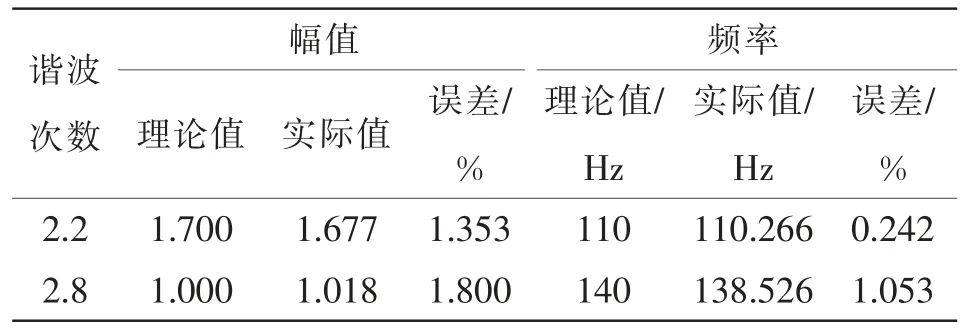
表2 算例2 的VMD-SWT 参数识别结果Tab.2 Parameter identification results based on VMD-SWT in case 2

4.3 实例信号分析

为更好地验证所提方法的有效性，采用文献[20]的实际电弧炉信号，采样频率和采样点数为4 096，在信噪比10 dB 时，对信号进行CWT 获得小波量图，如图8 所示。由图8 可见，存在3 条清晰的时频曲线，故将实际电弧炉信号分解成3 个模态分量，如图9 所示。

图8 电弧炉信号小波量图Fig.8 Wavelet map of electric arc furnace signal

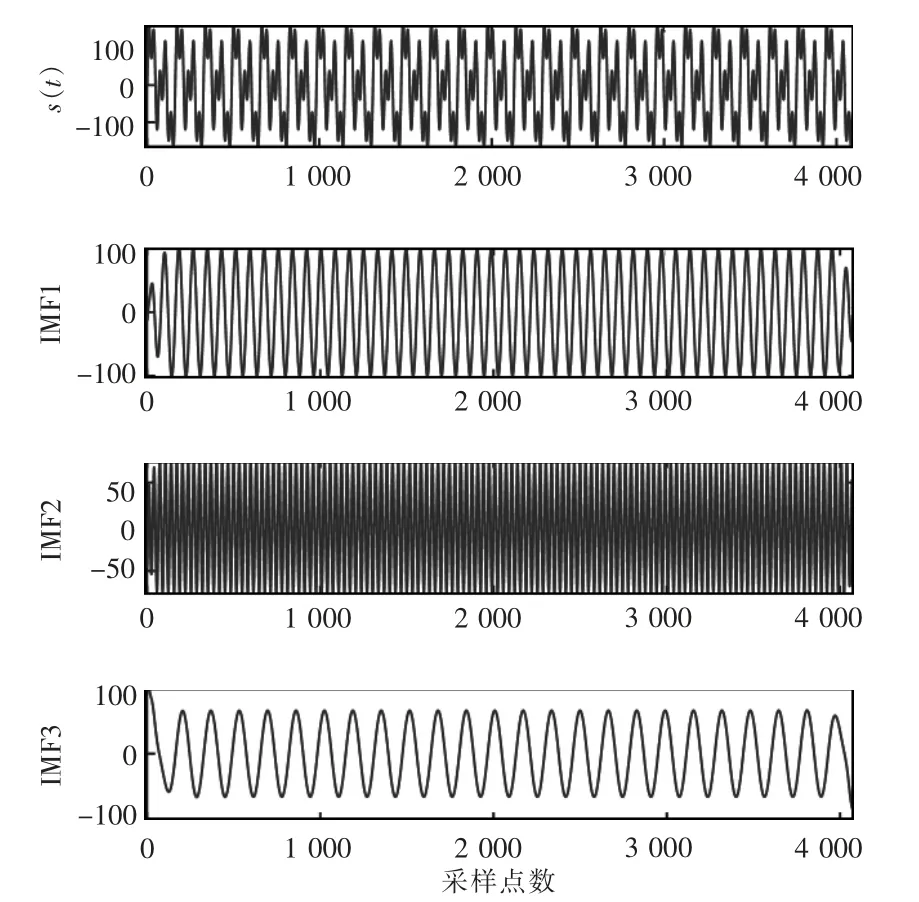
图9 电弧炉信号VMD 分解结果Fig.9 VMD decomposition result of electric arc furnace signal

SWT 识别电弧炉信号的瞬时频率、瞬时幅值及快速傅里叶变换FFT（fast Fourier transform）识别电弧炉信号的频率和幅值如图10—图12 所示。

由图10—图12 可以判断，该实际电弧炉信号由基波、125 Hz 和25 Hz 的间谐波组成，幅值分别为100、75、65[20]，这与文献中给出的实际值相符，模态提取效果较好，可以清晰分辨出基波和间谐波分量。VMD-SWT 算法精度较高，关键在于VMD 的模态分离能力和SWT 对小波系数的重组挤压，时频曲线得到细化。对于实际的含噪电弧炉信号，该算法依然表现出较好的噪声鲁棒性，这得益于VMD和SWT 的双重去噪，VMD 分解实际是多组维纳滤波过程，SWT 则在小波变换后，按设定的阈值自适应地过滤掉幅值较小的小波系数，故在噪声条件下VMD-SWT 算法仍可以准确提取模态并进行参数辨识，其参数识别结果见表3，为对比分析，表3 给出了FFT 算法的识别结果。

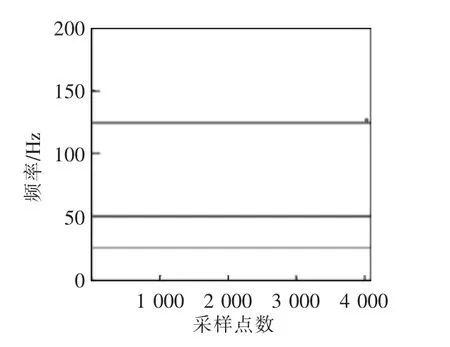
图10 SWT 识别电弧炉信号瞬时频率Fig.10 Instantaneous frequency of electric arc furnace signal identified by SWT

由表3 可知，VMD-SWT 算法频率识别的平均误差为0.338%，幅值的误差为0.045%，对比FFT 算法在幅值识别上存在优势，但在频率识别优势不明显，整体精度符合实际工程需要。无论分析直观图还是实际数据，该算法的模态提取能力较好、参数识别误差较小，表现出良好的抗噪性能。

图11 SWT 识别电弧炉信号瞬时幅值Fig.11 Instantaneous amplitude of electric arc furnace signal identified by SWT

图12 FFT 识别电弧炉信号的频率和幅值Fig.12 Frequency and amplitude of electric arc furnace signal identified by FFT

5 结论

本文提出VMD 和SWT 相结合的谐波/间谐波检测方法，经算例分析和实际数据得到如下结论。

（1）VMD 通过设置模态分解个数限制分解数量，可以有效提取模态分量，抑制模态混叠，分解实则为多个滤波过程，具有较强的抗噪声干扰能力。

（2）连续小波变换得到的小波量图可用于预判分量个数，提高VMD 算法的自适应性和运算效率。

（3）SWT 算法通过对小波量图重组挤压，改善小波脊线分辨率，锐化时频曲线，提高了检测精度。

（4）SWT 在挤压前根据设定的阈值滤掉一些幅值较小的小波系数，提高了算法整体的噪声鲁棒性。

此外，VMD 在分解时不可避免地存在端点效应，且迭代更新计算量大，实时性不高，后续可以就加快算法收敛速度以及谐波在线监测和改善展开研究，为实际应用提供有力的理论支持。