交错并联磁集成开关电感高增益Boost 变换器的研究

李洪珠，朱晓林，康庆华

（1.辽宁工程技术大学电气与控制工程学院,葫芦岛 125105；2.国网内蒙古东部电力有限公司通辽供电公司，通辽 028000）

工业革命给人类社会带来了经济的蓬勃发展，同时也使得人类对能源的依赖性大大提高。近些年，随着人们对化石能源的过度依赖和运用，化石能源逐渐枯竭，新能源的开发和利用已经迫在眉睫。风能和太阳能作为新能源首当其冲，通过统计数据可以了解到风能和太阳能的变化趋势基本相反，与传统发电系统相比，风光互补发电系统更加低碳环保，并且可持续发展，具有重大的现实意义[1-3]。随着新能源的迅速发展，变换器的性能也受到了很大关注，为了提高变换器的电气性能，近年来很多学者将磁集成技术、交错并联技术和开关电感等技术引用到直流变换器中，并取得了良好的效果。

实际生产中，为了使变换器输出电压保持稳定，通常会导致变换器的结构复杂、成本提高，还会出现系统稳定性差等问题。文献[4]提出了一种基于倍压单元的双输入高增益直流变换器，该变换器具有很高的电压增益，并且开关管应力有所减小，但是并没有对其中的电感进行磁集成；文献[5]对于级联变换器可以有效提高电压增益，但是主电路相对复杂，控制困难，保持变换器稳定工作也比较困难；文献[6]在传统Boost 变换器的基础上引入了储能电容模块，进行了移相控制，此时的电压增益并不是很高，而且没有进行磁集成，使得变换器有着很大的纹波；使用耦合电感同样可以提高变换器的增益，但是往往会引起开关管电压应力过高的问题，文献[7-9]通过多种方法去解决开关管电压应力的问题，但是会使电路过于复杂，或者控制策略困难。

本文在文献[6]的基础上，引入了开关电感，进一步提高电压增益，同时对变换器进行交错并联磁集成，减小电感电流纹波，提高变换器的暂态响应速度，减小变换器的体积以及开关管的电压应力，从而提高变换器的电气性能。

1 变换器的拓扑结构和工作模态

1.1 变换器的拓扑结构

交错并联磁集成开关电感高增益Boost 变换器的拓扑如图1 所示。

图1 交错并联磁集成开关电感高增益Boost 变换器拓扑Fig.1 Topology of interleaved high-gain Boost converter with magnetic integrated switched inductor

开关电感单元Ⅰ由电感L1、L2与二极管Di（i=5，6，7）组成，开关电感单元Ⅱ由电感L3、L4与二极管Di（i=8，9，10）组成。电感L1和L2正向耦合，电感L3和L4正向耦合，2 组开关电感进行反向耦合，正向耦合系数为M1，反向耦合系数为M2。C1=C2=C3，且足够大。

1.2 变换器工作模态

模态1（t0～t1）：此模态情况下的等效流通工作如图2（a）所示，开关管S1导通、S2关断，上一通道二极管D1、D5和D7导通，D3截止，下一通道D9和D4导通，D2、D8和D10截止，由此电感L1和L2并联。电源Vin对2 个电感充电，2 个电感绕组L1和L2处于并联充电状态，电感L1和L2中的电流iL1和iL2不断上升。正向耦合的2 个电感L3与L4处于串联状态，并且与电容一起对负载供电。模态1 的表达式为

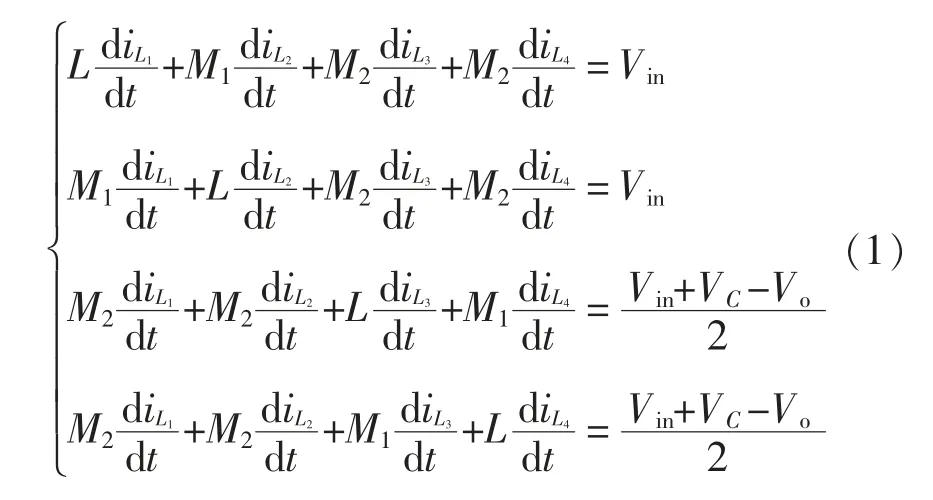
模态2（t1～t2）和模态4（t3～t4）：2 种模态情况下的等效流通工作如图2（b）所示，主开关管S1和S2都处于关断状态，上一通道二极管D3和D6导通，D1、D5和D7反向截止，下一通道D4和D9导通，D2、D8和D10关断。2 个电感绕组L1、L2与电容C1串联共同给负载供电，同时电感绕组L3、L4与电容C2串联给负载供电。模态2 和模态4 的表达式为

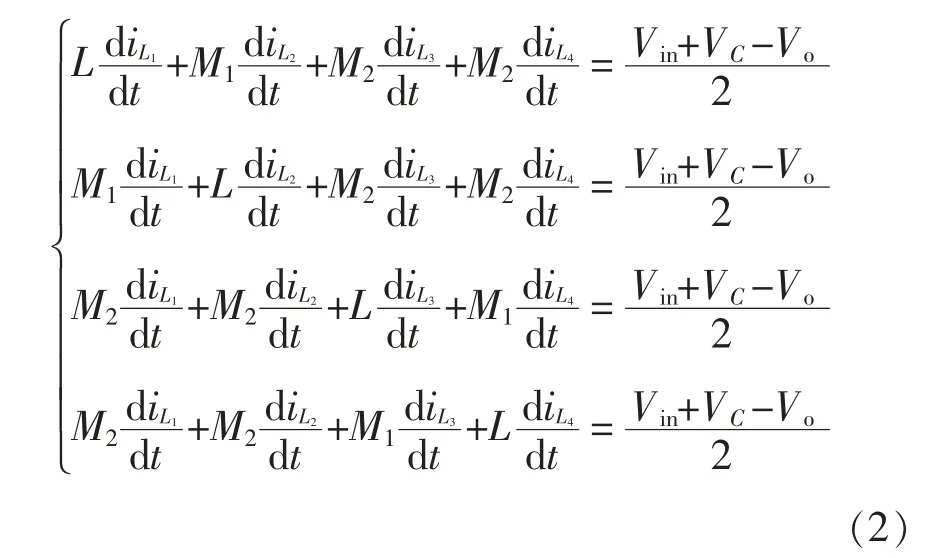
模态3（t2～t3）：此模态情况下的等效流通工作如图2（c）所示，开关管S2导通、S1关断，上通道二极管D3和D6正向导通，D1、D5和D7截止，2 个电感绕组L1、L2与电容C1串联共同对负载进行供电。电流iL1、iL2由于向负载端供电而不断下降，下通道体二极管D2、D8和D10导通，D4和D9截止，电感L3和L4与电容C2并联，电源Vin对电感和电容进行充电，电感电流iL3和iL4不断上升。模态3 的表达式为

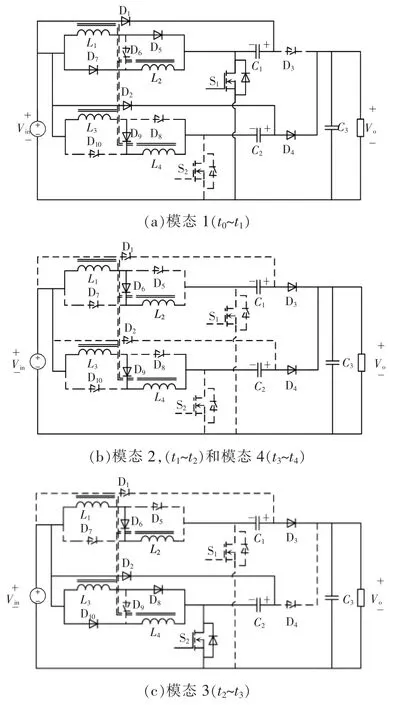
图2 4 个模态等效流通工作Fig.2 Equivalent circuit diagrams in circulation（in four modes）

2 变换器的工作性能分析

2.1 稳态电压增益

在变换器导通过程中，根据式（1）～式（3）以及电容C1、C2很大并且两端电压保持不变，能够得到支路电感中电流在4 个模态中的变化情况，如图3 所示。

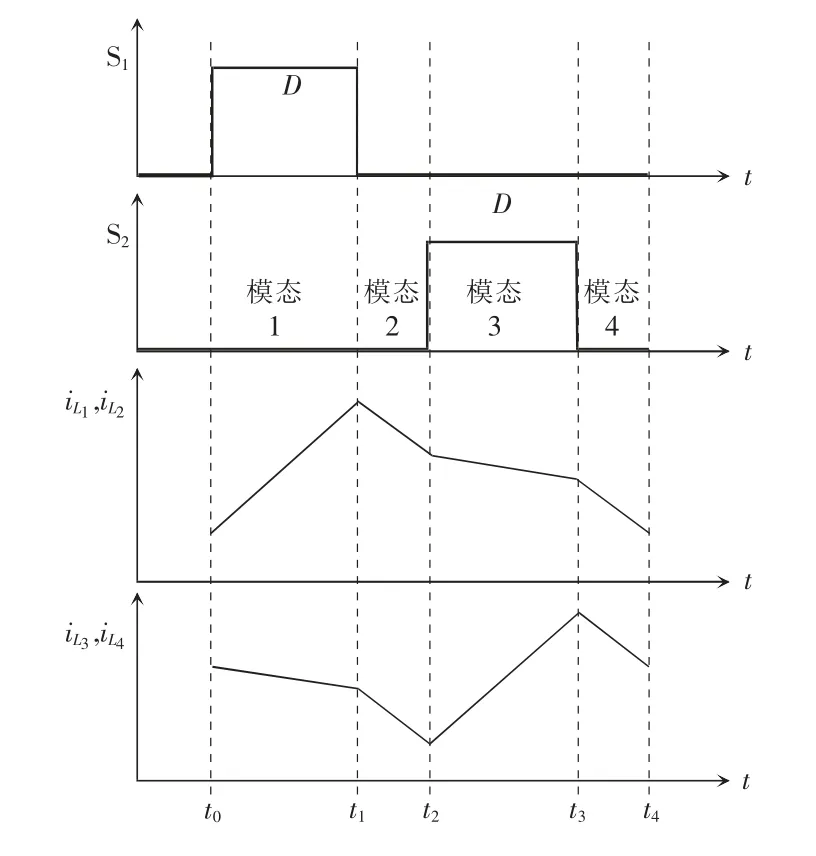
图3 变换器流通工作波形Fig.3 Working waveforms of converter in circulation

模态1：此模态情况下的工作时间是DT，其中D 为主开关管S1与S2在1 个周期内的占空比，T 为1 个工作周期时间，根据式（1）可得此模态时电流iL1的变化率为

模态2 与模态4：这2 个模态情况下的工作时间和为（1-2D）T，根据式（2）可得此模态时电流iL1的变化率为

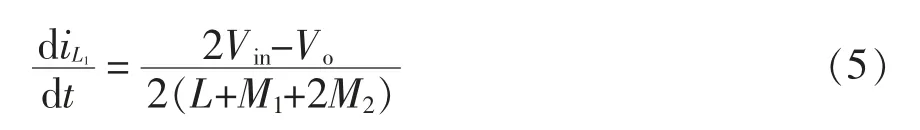
模态3：此模态情况的工作时间为DT，根据式（3）可得此模态时电流iL1的变化率为

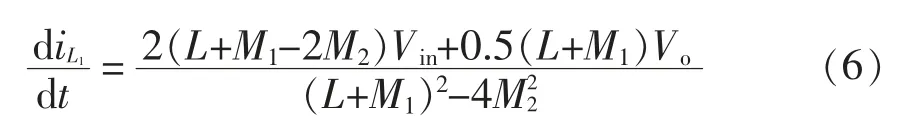
根据伏秒积定理，可以得到该变换器的电压增益为

由式（7）可以看出，本文提出的变换器比传统Boost 变换器增益提高了2 倍。

2.2 变换器支路等效稳态电感

通过分析可以得到变换器绕组采用耦合方式时，根据图4 和式（5）提出的变换器支路L1的稳态电流纹波为

式中，fs为主开关管的工作频率。

当变换器绕组采用非耦合的方式时，支路L1中电流如图4 所示，在电感绕组互相独立时变换器支路L1的稳态电流纹波为

式中，Ldis为非耦合时候的独立电感。

通过比较式（8）与式（9）可得，在耦合与非耦合2 种状况下，由于Leq1和Ldis的不同，造成了变换器支路的稳态电流纹波不一致的现象。因此本文提出的具有磁集成开关电感高增益Boost 变换器的支路等效稳态电感为Lss=Leq1，即

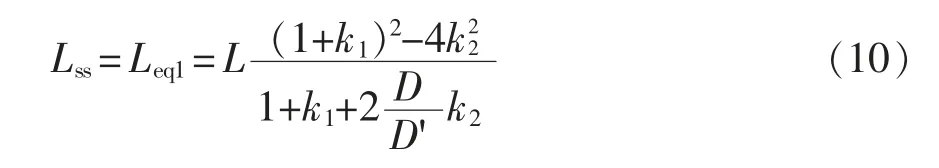
式中：k1为正向耦合系数；k2为反向耦合系数。

图4 变换器各模态情况的等效电感及支路稳态电流Fig.4 Equivalent inductance and steady branch current of the converter in different modes

2.3 变换器支路等效暂态电感

当直流变换器的负载突然变大时，为了保证输出电压在所要求的范围内波动而不至于跌落到最小极限值以外，要求系统有较快的反应速度。增大每相开关管的占空比可以提高变换器应对突增负载的响应速度。

交错并联磁集成开关电感Boost 变换器在工作过程中，当开关管占空比增大ΔD 时，支路L1中电感绕组流通电流的改变情况如图5 所示。

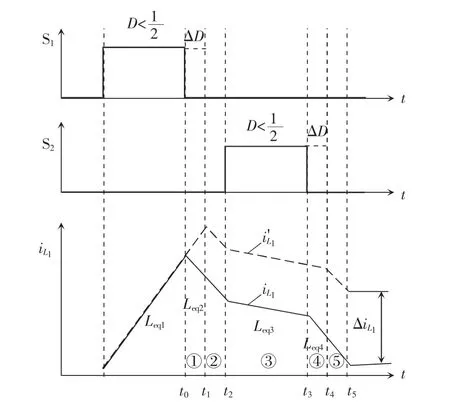
图5 耦合电感时变换器的暂态电流Fig.5 Transient current of the converter with coupling inductance

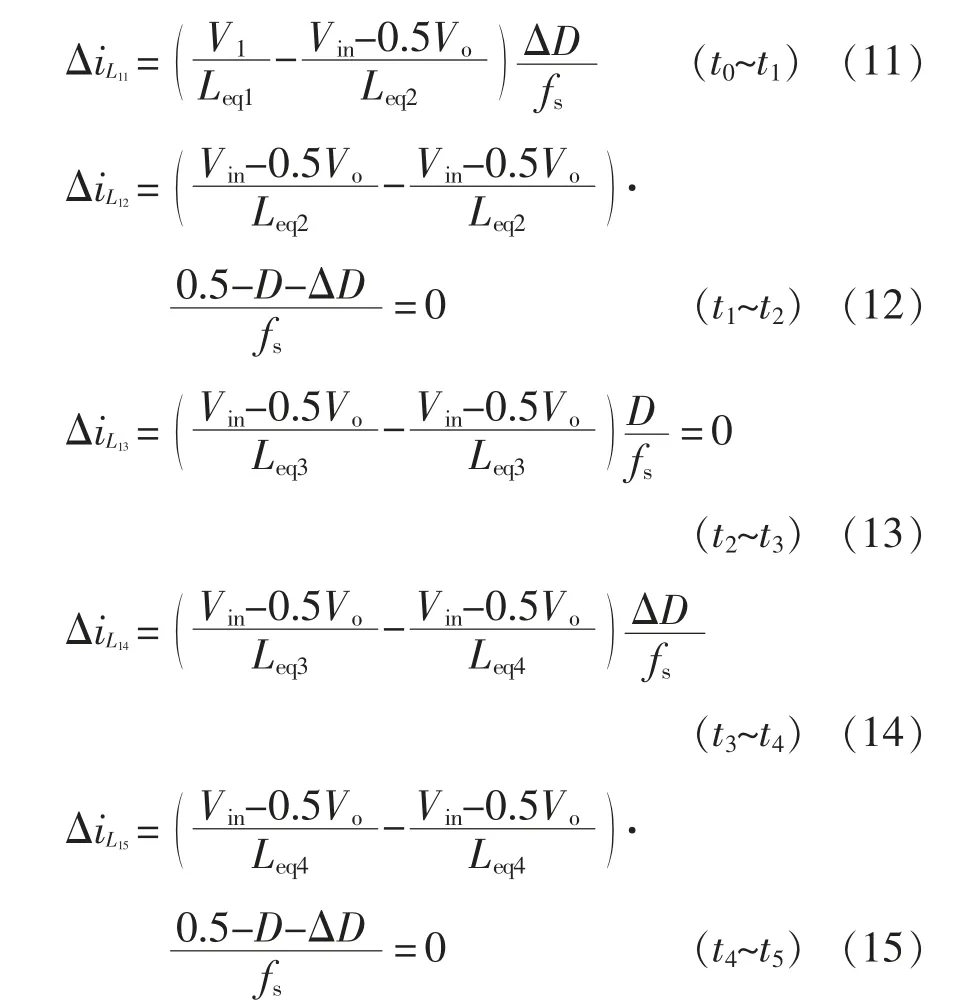
电感绕组L1支路中流通电流的暂态增量ΔiL1是以上各时间段增量之和，即

当变换器的电感绕组采用非耦合方式，在开关管占空比增大ΔD 时，支路L1中电感绕组电流的变化情况如图6 所示。

图6 具有独立电感时变换器的暂态电流Fig.6 Transient current of the converter with independent inductance

由图6 可知

根据图6 及式（17）和式（18）可得

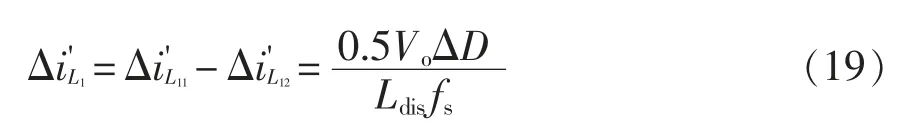
通过比较式（16）与式（19）可知，变换器支路暂态电流增量在耦合和非耦合2 种形式下有差异是由于Leq2和Ldis不一致造成的。因此本文提出的交错并联磁集成开关电感Boost 变换器的支路等效暂态电感为Ltr=Leq2，即

通过对比式（9）与式（19）可知，因为在非耦合条件下变换器的支路稳态电感与支路暂态电感相同都为Ldis，所以电感绕组支路的稳态电流纹波与暂态电流响应速度是相互矛盾的2 个变量。即要想通过降低独立电感值Ldis实现提高暂态电流响应速度，必然将增大支路的稳态电流纹波，反之亦然。

但在耦合条件下，通过对比式（4）与式（13）可知，支路稳态电感Leq1与暂态电感Leq2不一致，所以能够采用调节正向耦合系数k1和反向耦合系数k2的方式来提高Leq1或降低Leq2。因此，在降低支路稳态电流纹波时能够实现保持支路暂态电流响应速度不发生变化；或者在提高支路暂态电流响应速度时能够实现保持支路稳态电流纹波不发生变化；再者可以实现既降低支路稳态电流纹波，又提高支路暂态电流响应速度，从而解决非耦合条件下的矛盾问题，进而提高变换器的电气性能。

2.4 电感耦合度的设计准则

由式（8）与式（9）及式（16）与式（19）能够得到耦合与非耦合2 种条件下支路的稳态电流纹波之比和暂态电流响应速度之比，即

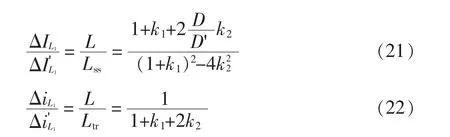
由式（21）和式（22）可知，进行磁集成后电感稳态电流纹波、暂态响应与正反相耦合度及开关管的占空比有关。电感耦合对稳态电流纹波及暂态电流响应速度的影响程度可以分别用等效稳态电感Lss及等效暂态电感Ltr与非耦合条件下的独立电感L的比值来衡量对比，其比值与k1、k2和D 之间的关系如图7 所示。图7 给出了当k1分别等于0.2、0.4、0.6、0.8 和1.0 时的比值，每幅图中又给出了D 分别等于0.1、0.2、0.3 和0.4 时的Lss与L 的比值曲线，如图中实线所示。

分析图7 可以得出以下结论。

（1）由图7（a）～（e）可得，随着正向耦合系数k1的逐渐增大，反向耦合系数k2可设计的有效范围也变大，由[-0.6～0]区间到[-1.0～0]区间。

图7 等效稳态电感Lss 及暂态电感Ltr 与独立电感L 的比值曲线Fig.7 Curves with ratios of Lss/L and Ltr/L

（2）由任意一图可知，当k1和k2保持不变时，随着D 的增大Lss/L 会增大，即稳态纹波会减小；当k1和D 保持不变时，随着|k2|的增大，变大，Ltr/L 会变小，此时，Lss/L 也会变小；当k2和D 不变时，随着k1的增大，Lss/L 增大。

（3）当Ltr/L 比值不变，即变换器的暂态电流响应速度不变时，随着正向耦合系数k1的增大，Lss/L 的值也增大，并且D 增大时可以进一步提高Lss/L 的值，即进一步减小。这样在保持支路暂态电流响应速度不发生变化的条件下，能够降低支路的稳态电流纹波。

（4）当Lss/L 比值不变即变换器的支路稳态电流不变时，为了提高变换器的暂态性能，可以通过调节k2来实现。随着k1的增大应该逐渐增大|k2|，通过这种方法既保持了稳态电流不变，又提高了暂态性能。

（5）为了减小支路稳态电流纹波，k1值越大越好，同时可以调节k2的值来减小Ltr/L 的值，这样能够通过调节k1和k2的值实现既降低支路稳态电流纹波又提高暂态电流响应速度。

通过以上理论分析可知，合理的电感耦合度设计，既能减小变换器的稳态电流纹波，又能提高其暂态响应速度，解决了前文所提出的矛盾，进而可以提高变换器的电气性能。

3 仿真

在PSIM 仿真环境下对本文所提高增益Boost变换器进行模拟仿真，其仿真建模如图8 所示。其中输入端电压Vin=12 V，开关频率为100 kHz，负载电阻R=4 Ω，电感L=10 μH，电容C=1 000 μF，正向耦合系数k1=0.96，反向耦合系数k2=0.4，占空比D=0.33。

图8 为变换器在耦合情况下输出电压仿真示意，在输入电压Vin=12 V 的条件下，输出电压Vo≈36 V，验证了输出、输入两端电压关系式Vo/Vin=2/（1-D）的正确性。

图8 变换器输出电压仿真波形Fig.8 Simulation waveform of voltage output from the converter

图9（a）是变换器正常工作过程中耦合条件下电感支路的电流波形，由图可知耦合情况下电感支路电流纹波约等于2.1 A；图9（b）是变换器正常工作过程中电感独立条件下电感支路的电流波形，由图可知非耦合情况下电感支路电流纹波约等于3.96 A。比较图9（a）和（b）可知，对电感磁集成后能够在很大程度上减小电感支路的电流纹波。

图9 耦合与非耦合情况下的支路中流通电流仿真波形Fig.9 Simulation waveforms of branch current with coupling or independent inductance

4 实验

对本文所提交错并联磁集成开关电感高增益变换器进行实验验证，工作过程中，设置输入端电压Vin=12 V，频率是100 kHz，占空比D=0.33。其中的磁芯材料是锰锌铁氧体磁芯，采用EE 磁芯进行磁集成。M12和M34为正向耦合系数，M13和M14、M23和M24为反向耦合系数，耦合电感的自感互感参数如表1所示。样机实物及实验系统平台如图10 所示。

表1 耦合电感实验数据Tab.1 Experimental data of coupling inductance

图10 样机实物及实验系统平台Fig.10 Prototype and experimental system platform

图11 是变换器工作时输出电压波形，此时的输入电压Vin=12 V，根据理论分析可知高增益Boost 变换器增益Vo/Vin=2/（1-D），则输出电压应为36 V，而传统的Boost 变换器输出应为18 V。图11（a）的输出实验电压为36 V 左右，图11（b）的输出实验电压为18 V 左右，与理论分析相符。

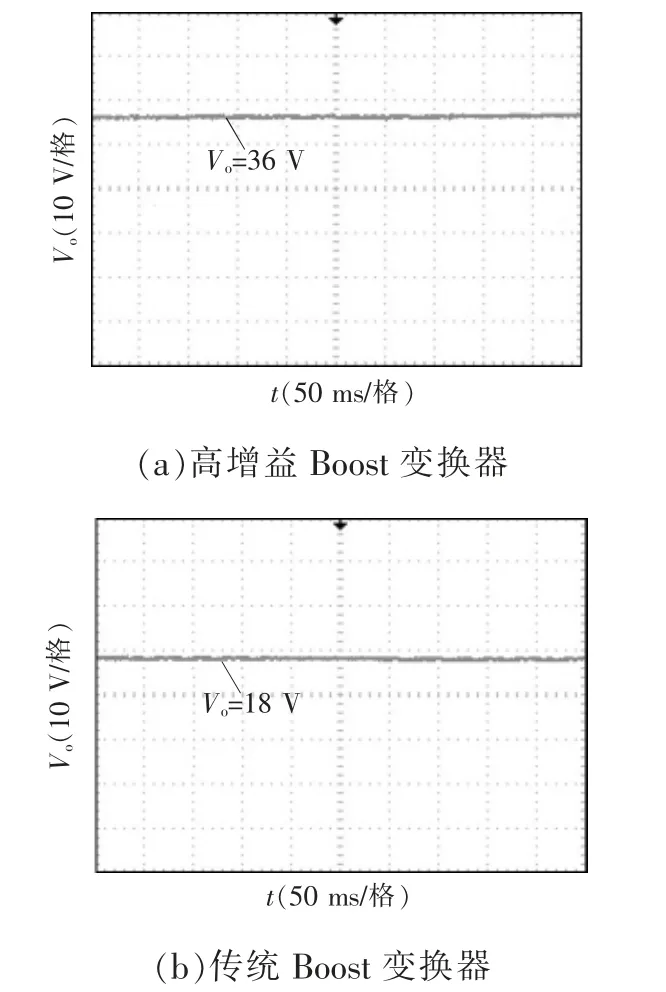
图11 输出电压实验波形Fig.11 Experimental waveforms of output voltage

图12 是变换器工作在稳态时，耦合与非耦合2 种条件下的电感支路电流实验波形。图12（a）为耦合情况下电感支路电流，此时电流纹波大约为1.95 A，图12（b）为非耦合情况下电感支路电流，此时电流纹波为4.2 A。比较可见，耦合情况下纹波明显减小，由此可以证明，对电感进行磁集成后可以有效减小稳态电流纹波，与耦合电感设计准则和理论分析相符合。

图12 导通过程中耦合及非耦合2 种条件下支路电流纹波Fig.12 Branch current ripple in the conduction process with coupling or independent inductance

当输出侧负载突然增加时，变换器在耦合与非耦合2 种情况下的输出电压波形如图13 所示。由图13（a）可知，电感耦合条件下变换器暂态响应速度为28 ms；由图13（b）可知，电感非耦合条件下变换器暂态响应速度为48 ms。通过对比可得，电感经过磁集成处理后能够提高暂态响应速度，改善变换器的动态电气性能，验证了前文的理论分析。

图13 暂态响应实验波形Fig.13 Transient response experimental waveforms

图14 为开关管电压应力。根据理论分析可知，D3的开关管应力应与D1和S1互补，VD3=VD1=VS1=（1+D）Vo/2，当输入为12 V，占空比D=0.33 时，VD3=VD1=VS1=24 V，实验结果显示，3 个开关管的电压应力为24 V 左右且波形互补，与理论分析结果基本相符。

图14 功率器件电压应力Fig.14 Voltage stress in power devices

5 结论

本文提出一种交错并联磁集成开关电感高增益Boost 变换器，理论分析和实验结果表明，该变换器较传统变换器具有以下优点。

（1）新提出的变换器的电压增益是传统交错并联Boost 变换器电压增益的2 倍；

（2）变换器中的电感经过磁集成处理降低了支路电流纹波，提高了暂态响应速度；

（3）变换器开关器件的电压应力比传统Boost 变换器有所降低。

综上所述，该变换器具有良好的工作性能，适用于燃料电池、不间断电源和光伏发电等需要高增益直流变换器的新能源系统工业领域。