基于PWM+PFM 的LLC 谐振变换器软启动研究

赖 娜，杜贵平，雷雁雄，刘源俊

（华南理工大学电力学院，广州 510641）

LLC 谐振变换器以其高频、高效、高功率密度等优点，在各领域中得到广泛应用。但LLC 谐振变换器启动过程中电流冲击大是一个不容忽视的问题。一方面，在分析LLC 谐振电路时，均假设输出电容足够大，以保证输出端电压被箝位。但在实际启动阶段中，LLC 谐振变换器对大容量滤波电容的充电过程使得电路产生较大的电流冲击，从而可能毁坏电路中的功率器件或引发电路保护[1]；另一方面，由于工作在谐振频率处，LLC 谐振变换器中的谐振腔阻抗非常小，导致谐振腔本身产生很大的电流[2]。电路中过大的电流冲击容易造成功率器件发热损坏，并影响系统的动态特性。

为抑制启动过程中的电流冲击，使LLC 谐振变换器安全稳定的启动，研究学者们在此方面做了深入研究。文献[3-4]采用在电路中增加吸收电容和箝位二极管的方法，通过箝位谐振电容上的电压，谐振槽的阻抗自动增大，有效地限制了通过谐振槽的电流，但该方法增大了系统成本及损耗。为获得较好的动态性能，轨迹控制方法[5-7]被应用于对软启动过程进行优化，通过感应谐振电感电流、谐振电容电压、输入电压及输出电压计算非线性变量，并基于状态平面分析，从而抑制谐振腔电流冲击。该方法具有一定的优化效果，但控制方法复杂，计算量大、耗时长，在高频工作环境下并不可取[8]。文献[9-10]采用的平均电流法能改善变频器的瞬态响应，但需要高带宽和高精度的电流传感器来快速实现电流控制。而脉宽调制[1,11]及变频控制[12-13]具有结构简单、控制方便等优点，被广泛应用于LLC 谐振变换器的软启动过程中。其中文献[1]通过模态分析，绘制出占空比与电压增益的关系曲线，设置了启动过程中占空比的变化函数，从而抑制启动过程中的电流冲击。该方法效果明显，但在启动初期，占空比变化曲线的斜率很小，大大增加了启动过程的稳定时间；在启动后期，占空比变化曲线的斜率很大，输出电压动态性能差。

为优化软启动过程中的电流抑制效果，本文基于文献[1]对全桥LLC 谐振变换器的软启动过程，根据数学计算切换2 种脉宽调制方法，同时引入变频控制，设计一种新型软启动控制策略，通过理论分析及实验验证，该方法能够减小传统全桥LLC谐振变换器启动过程中电流冲击，提高输出电压动态特性，使电路启动时更加稳定可靠。

1 启动过程中LLC 谐振变换器的工作原理

图1 为全桥LLC 谐振变换器主电路，M1—M4构成一个全桥变换器，Lr为谐振电感，Cr为谐振电容，Lm为变压器T1的励磁电感，副边二极管D1、D2交替工作为负载供电。

图1 全桥LLC 谐振变换器主电路Fig.1 Main circuit of full-bridge LLC resonant converter

不同于两谐振电路的时域分析，LLC 谐振变换器各工作模态切换复杂，无法得到增益的显性表达式，求解出精确的解析解。基波分量法分析过程简便直观，被广泛应用于求解谐振变换器的增益关系。基波分量法假设能量传递只与谐振槽电压电流的基波分量有关，忽略高次谐波成分的影响。

考虑整流电流与变压器输入端电压的相位关系，将变压器及副边电路等效为一个交流等效电阻Rac[14]。从而将LLC 谐振电路等效为一个向阻性负载传递能量的线性电路，通过图2 所示的基波等效电路分析LLC 电路的直流增益特性。

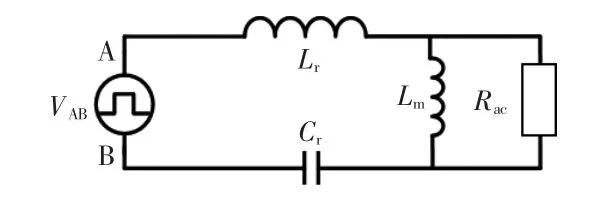
图2 基波等效电路Fig.2 Fundamental-wave equivalent circuit

由该等效模型，列出其电压传递函数，进行模值计算，可得归一化电压增益为

由式（1）可得LLC 谐振变换器增益随归一化频率变化的曲线，如图3 所示。显然，在保证最大增益的同时，应选择尽量大的Q 值，以保证在较窄的调频范围内实现较大的输出电压范围，以图3 中Q=0.10 时的增益曲线为例分析软启动过程。

在分析LLC 谐振电路时，将输出电容设置的足够大，以保证正常工作时输出端电压被箝位。但启动阶段中，由于电容电压不能突变，根据可知，LLC 谐振变换器突增的电源电压对该输出电容的充电过程使电路产生较大的电流冲击，其变化过程如图4（a）所示。LLC 谐振变换器稳定工作时谐振腔电流并不大，但在开机瞬间达到稳态值的几十倍，可能毁坏电路中的功率器件或引发电路保护。

降频控制是LLC 谐振变换器常用的软启动方式，图4（b）为初始频率为2fr时启动过程中谐振电流的变化过程，电流冲击抑制效果明显，但在启动初始时刻仍然存在很大的尖峰值。由图3 中增益曲线上的频率变化轨迹可以看出，为达到较好的电流抑制效果，须将初始频率设置得尽量高。但实际主开关器件、驱动电路及控制器的速度限制，使该方法在软启动过程中难以达到理想的电流抑制效果。

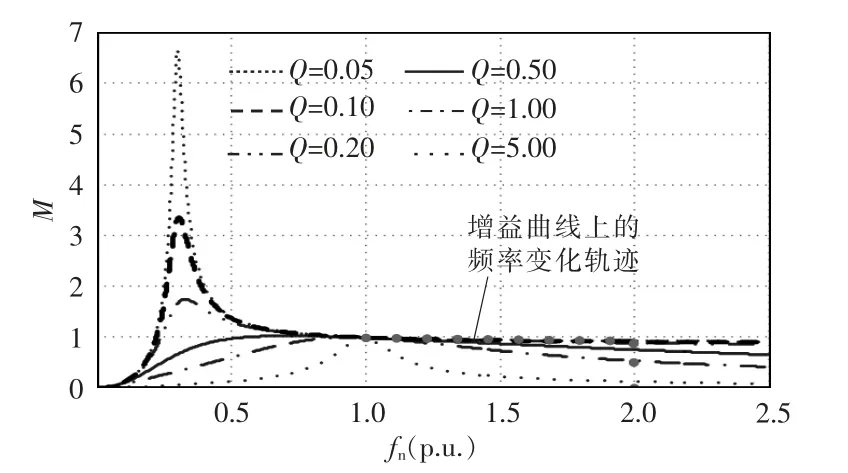
图3 h=10 时，LLC 谐振变换器的调频增益曲线Fig.3 Gain curve of LLC resonant converter with frequency modulation at h=10

图4 不同软启动控制策略下谐振电流的仿真波形Fig.4 Simulation waveforms of iLr under different softstart control strategies

解决方案在软启动过程中采用降频控制的同时引入PWM 控制。文献[15]采用时域分析法，通过分析各个模态变化情况，绘制出PWM 控制时在不同品质因数下增益M 关于占空比Dy的曲线，如图5 所示。

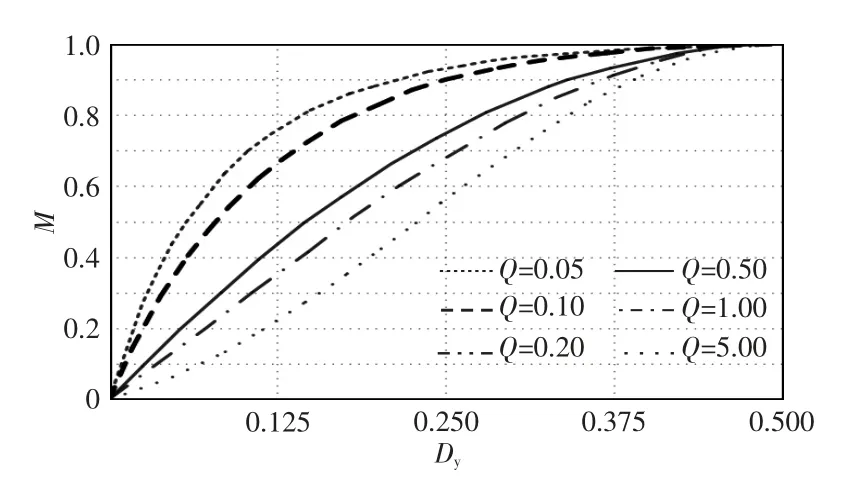
图5 h=10 时，LLC 谐振变换器的PWM 控制增益曲线Fig.5 Gain curve of LLC resonant converter with PWM at h=10

启动过程中调节占空比可改善输出电压的上升速度，实现逐周期限流。从LLC 谐振变换器的PWM 控制增益曲线（图5）看出，Q=0.10 时，在占空比较小处，M 随Dy的增加上升的非常快，此时在软启动过程中设置占空比直线上升，电流冲击仍然较大；在占空比较大处，占空比对输出电压的调节作用明显，此时在软启动过程中设置占空比快速上升，输出电压快速建立使得电流冲击增大。由于无法列出增益M 与占空比Dy的显性表达式，难以准确地设置出软启动过程中电流抑制效果较好的占空比变化曲线。

为解决上述问题，根据传统PWM 控制方法的电流抑制情况，本文提出一种新的变占空比方法，并结合降频控制对软启动过程实施混合控制，优化电流抑制效果的同时，能在较窄的调频范围内实现软启动过程，并适用于全负载范围。

2 PWM+PFM 混合控制策略

根据nVo=VinM，其中变压器变比n 及输出电压Vin为固定值，显然，通过改善软启动过程中电压增益M 随时间t 的变化情况可以达到限流的目的。为优化电流冲击的抑制效果，本文提出一种将调频和脉宽调制相结合的思想，即根据脉宽调制时增益随占空比递增的特性，在软启动过程中切换2 种脉宽调制方法，得到一种新的占空比变化曲线，同时根据调频控制时增益在最大开关频率至额定工作频率间逐渐递增的特性，提出一种基于PWM+PFM 的LLC 谐振变换器软启动控制策略，进一步优化谐振电流冲击的抑制效果。此外，该策略在启动阶段对调频控制的起始频率并无太高要求。

对基波等效电路进行计算得到LLC 谐振变换器的软启动时间。谐振腔输入电压VAB为对称方波，通过傅里叶分解得到

再将式（2）进行拉普拉斯变换，得到复频域的输入信号为

根据图2 列出其开环传递函数为

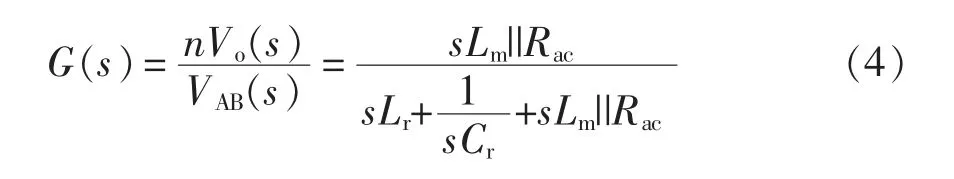
系统输出C（s）=R（s）G（s）经过反拉斯变换得到该系统响应曲线，则可得到其电压上升时间。为保证软启动方法抑制效果较好及系统稳定时间较短，将软启动时间设置成该值的3～5 倍。

启动时，将LLC 变换器频率设置成2 倍的额定工作频率，在启动过程中逐渐减小，启动结束时，恰好降至额定工作频率处，调频的同时逐周期改变LLC 变换器的占空比。脉宽调制时增益与占空比成正相关，启动过程中占空比随工作周期的变化情况会影响系统的软启动效果。

图6 给出了全桥LLC 谐振变换器在4 种启动方式下占空比随时间变化的曲线图。曲线a 为占空比随时间呈直线形式上升；曲线b 为占空比随时间呈幂函数形式上升；曲线c 由a、b 曲线拼接得到；曲线d 为本文所提的变占空比。

图6 PWM 控制时占空比变化曲线Fig.6 Changing curve of duty cycle under PWM control

传统软启动方法是使占空比在启动过程中呈直线形式变化，其占空比变化的表达式为

而文献[1]通过模态分析，提出了一种占空比随时间呈幂函数形式变化的软启动方法，从而抑制启动过程中的电流冲击。其占空比变化的表达式为

结合上述2 种占空比变化方式，本文提出一种新的占空比变化曲线，在软启动前期使占空比随时间呈幂函数形式变化，在软启动后期使占空比随时间呈直线形式变化，直至占空比达到额定值。其具体设计的方法如下。

（1）将上述2 种占空比变化曲线a、b 直接拼接，得到占空比变化曲线c。

（2）为使各软启动过程时间相等，再经过比例收缩得到本文所述的变占空比曲线d，其表达式为

式中：Dy_max为变换器的额定占空比；tr为变换器启动时间，可通过调节tr的值改变软启动效果；Tchang为2 种传统占空比变化曲线的切换时刻，此时两条占空比变化曲线a、b 的斜率相等，即

图7 给出了LLC 谐振变换器4 种软启动方式下的仿真波形，其中：①直接启动；②占空比直线形式上升；③占空比呈幂函数形式上升；④PWM＋PFM混合控制。仿真时设置软启动时间tr为25 ms。从仿真图中可知，采用PWM＋PFM 混合控制方法可使输出电压在启动过程中平稳建立，相对于2 种传统的变占空比方法，进一步降低了电路中的电流冲击，减小了开关器件的应力。

图7 不同软启动控制策略下的仿真波形Fig.7 Simulation waveforms under different soft-start control strategies

3 实验结果

搭建一台最大功率为200 W 的全桥LLC 谐振变换器样机进行验证。样机所选元件如下：控制芯片为TMS320F28035（TI）；高压侧开关管为SPW24 N60CFD（额定电流为21.7 A）；低压侧开关管为VSAPH3006-F3（额定电流为30 A）。变换器主要实验参数如表1 所示。

表1 实验参数Tab.1 Experimental parameters

基于已搭建的全桥LLC 谐振变换器样机，分别实施上述不同软启动方法进行控制，得到各软启动方式下谐振电流iLr和输出电压Vo的实验波形，将额定占空比设置为43.75%，软启动时间设置为0.025 s。其中PWM 控制时，变换器工作在200 kHz情况下；降频控制时，变换器工作频率从400 kHz降低至200 kHz；PWM＋PFM 混合控制时，工作频率设置从400 kHz 逐渐降低至200 kHz，占空比按照图5 中d 曲线变化规律由小增大，2 种方法在启动过程中同时调制。当启动结束时，变频器在调频控制下工作。

实验结果如图8 所示，与上文的仿真结果一致。图8（a）为直接启动时的实验波形，启动时刻谐振电流iLr振荡剧烈，电流过冲大；图8（b）为占空比呈直线上升时的实验波形，电流冲击减小至7.6 A；图8（c）为占空比呈幂函数形式变化时的实验波形，电流冲击减小至9.3 A；图8（d）为本文所述变占空比脉宽调制方法下的实验波形，电流冲击减小至7.6 A。相较于占空比直线上升的脉宽调制方法，本文所提的变占空比曲线中占空比在启动前期变化较缓慢，进一步降低了LLC 谐振变换器在启动过程中产生的电流冲击。相较于占空比呈幂函数形式变化的脉宽调制方法，本文所提的变占空比曲线中占空比在软启动前期变化较快，有效减小了启动过程中输出电压的稳定时间。

全桥LLC 谐振变换器的启动过程中，采用本文所提的变占空比控制策略，电流冲击明显减小，但仍须进一步优化。在此基础上，增加降频控制，在启动过程中实现混合控制。降频控制的实验波形如图8（e）所示，本文提出的PWM+PFM 混合控制策略实验结果如图8（f）所示。从实验波形可以看出，采用混合控制策略，在较窄的频率范围内也能提高电路的电流冲击抑制能力和谐振电流暂态过程的稳定性。图9 为满载时PWM+PFM 混合控制方法下的实验波形，此时电流的峰值为10.7 A，可以看出满载情况下该方法依然能有效抑制电路中的电流冲击。

图8 不同控制策略下轻载启动的实验波形Fig.8 Experimental waveforms of light load start-up under different control strategies

图9 混合控制下满载启动的实验波形Fig.9 Eexperimental waveforms of full-load start-up under hybrid control

所述6 种软启动方法的实验结果表2 所示，相比于直接启动，采用PWM+PFM 混合控制策略的情况下，谐振电流冲击减小了450%，有效抑制了电路中的电流冲击。其他几种软启动方法中，占空比呈直线变化的PWM 控制方法效果最优，但该方法仍然比PWM+PFM 混合控制策略下的谐振电流冲击高出19%。从结果分析可得，所提控制策略能大幅度降低谐振电流暂态过程的峰值，并保持较短的系统稳定时间，验证了其可行性和有效性。

表2 实验结果Tab.2 Experimental results

4 结语

本文对全桥LLC 谐振变换器的软启动控制进行了研究，通过增益特性分析，传统PWM 控制及PFM 控制在软启动过程中电流抑制效果不佳。本文所提PWM+PFM 混合控制策略，在优化电流抑制效果的同时，能在较窄的调频范围内实现软启动过程。搭建仿真模型和实验平台对各软启动方法进行实验，经对比分析，相对于PWM 控制及PFM 控制，本文提出的控制策略软启动效果更优，能大幅度降低谐振电流暂态过程的峰值，并保持较短的系统稳定时间。即该策略具有可行性及有效性，能改进全桥LLC 变换器的启动过程，并提高变换器的可靠性和安全性。