一种MMC 子模块电容电压波动最小化容值优化方法

韩 啸，李 睿

（电力传输与功率变换控制教育部重点实验室（上海交通大学），上海 200240）

模块化多电平变换器MMC（modular multilevel converter）在直流配电领域获得了广泛的应用。与传统的两电平拓扑相比，MMC 具有以下明显的优势：MMC 的每个桥臂由多个标准子模块SMs（submodules）串联而成，多个子模块不需要同时导通或关断，可降低电压变化率；相同等效开关频率下开关管的开关频率更低，减小了变换器的损耗；子模块采用分布式直流电容，容易得到较高的输出电平数，使变换器交流侧电压和电流更接近理想的正弦波，可以减小甚至省去换流站的大容量交流滤波器；电抗器串联在上下桥臂之间，使直流侧短路时故障电流的上升率限制在较低的水平；模块化设计使系统易于实现扩展和冗余，系统容量提高，稳定性增强[1-3]。然而，MMC 拓扑也存在一些缺点。由于其所有的子模块电容为悬浮状态串联在桥臂中，桥臂电流含直流分量、一倍频分量与二倍频分量，桥臂电压含直流分量与一倍频分量，因此桥臂功率含一倍频、二倍频和三倍频交流分量，这些交流分量作用在电容上，导致子模块电容电压存在波动，尤其当变换器容量提升时，需要使用较大的电容才能将子模块电容电压的波动限制在合理的范围内[4-5]。子模块电容的成本大约是整个子模块成本的1/3，而子模块电容的重量和尺寸却占整个子模块很大的比例。减小子模块电容对降低系统成本、提高变换器功率密度、实现变换器的轻型化具有重要意义，因此必须采取一定措施，以减小子模块电容[6]。

近年来，国内外学者提出了一些减小MMC 电容的方法，主要分为改进拓扑类方法和附加控制类方法[7-9]。由于目前实际应用中MMC 拓扑以半桥子模块为主，从成本和实现难度的角度考虑，附加控制类方法是工程中常用的方法。附加控制类方法通过注入特定环流和电压以改变相间环流和桥臂电压等物理量来减小电容电压波动。文献[10]通过抑制相间环流的方法减小了子模块电容电压波动，但其没有利用MMC 中环流这一特有的自由度；文献[11-13]通过注入在线计算的环流来减小子模块电容电压的波动，但在线计算在实际应用中实现较复杂；文献[14-15]通过注入离线计算的二次环流和三次共模电压，消除了电容电压波动的二倍频分量，可以将子模块容值需求降低至常规方法的1/3。以消除二倍频的子模块电容电压波动或桥臂功率波动为优化目标虽然有一定效果，但已有方法没有利用电容电压波动的解析表达式分析不同注入成分对电容电压波动幅值的直接影响。

本文针对典型半桥MMC 系统，首先简要介绍了MMC 的工作原理，建立了子模块电容电压波动的数学模型。然后分析了电容电压纹波随所注入共模电压和环流的变化规律，在此基础上提出了一种新的优化方法。从电容电压波动的精确解析表达式入手，注入合适幅值和相位的三次共模电压和二、四次环流，选取最优调制比，使目标函数电容电压纹波达到最小化，从而在一定电容电压波动率下使其电容取值达到最小化。所提方法可以将子模块容值的需求降低至常规方法的22%，变换器功率损耗降低至常规方法的87%。最后，用RT-LAB 实时仿真验证了所提方法的有效性。

1 MMC 工作原理

三相MMC 电路模型如图1 所示。MMC 的拓扑结构如图1（a）所示，它由3 个相单元组成，每个相单元由上下两个桥臂组成，每个桥臂又由N 个子模块和一个桥臂电感串联构成。桥臂电感为MMC 提供限制和控制桥臂电流的能力。3 个上桥臂的连接点为正直流母线，3 个下桥臂的连接点为负直流母线。子模块拓扑结构为半桥HB（half-bridge）电路，它由2 个开关管（S1、S2）和一个直流电容（C）组成。采用脉冲宽度调制PWM（pulse width modulation）法控制每个子模块开关管的脉冲，使每个子模块的输出电压均为带直流偏置的正弦波，所有子模块的输出电压叠加得到桥臂电压，上下桥臂之间中点的电压为交流相电压。因此，MMC 可以实现AC/DC 或DC/AC 的变换。

假定MMC 的3 个相单元参数完全相同，上下桥臂参数对称，仅以a 相为例进行分析。a 相的等效电路模型如图1（b）所示。直流母线电流Id在3 个相单元中平分，a 相交流电流ia在上下桥臂中平分，忽略相间环流，则上下桥臂电流ipa和ina分别表示为

a 相交流电流ia的表达式为

式中：Im为交流侧a 相电流幅值；ω 为电网角频率，ω=2πf，f=50 Hz；t 为时间。直流母线电压Ud在上下桥臂中平分，该交流相电压ua为变换器交流侧的电压，则上下桥臂电压upa和una分别表示为

由于MMC 在正常工作情况下交流侧功率因数为1，电压ua与电流ia同相位，则ua表示为

式中，Um为交流侧a 相电压幅值。

图1 MMC 电路模型Fig.1 Circuit models of MMC

2 MMC 子模块电容电压波动分析

假定所有子模块电容电压均压良好，子模块电容平均电压Uc与直流母线电压Ud的关系为

当MMC 工作在稳态时，子模块输入功率在0处上下波动，一个交流周期内子模块电容电压在平均值Uc附近波动，如图2 所示。图中：upai为单个子模块输出电压；ipa为a 相上桥臂电流；ppai为单个子模块的功率，即upai与ipa的乘积；Uc为电容电压平均值，也即电容电压直流分量；uc为子模块电容电压的交流分量。

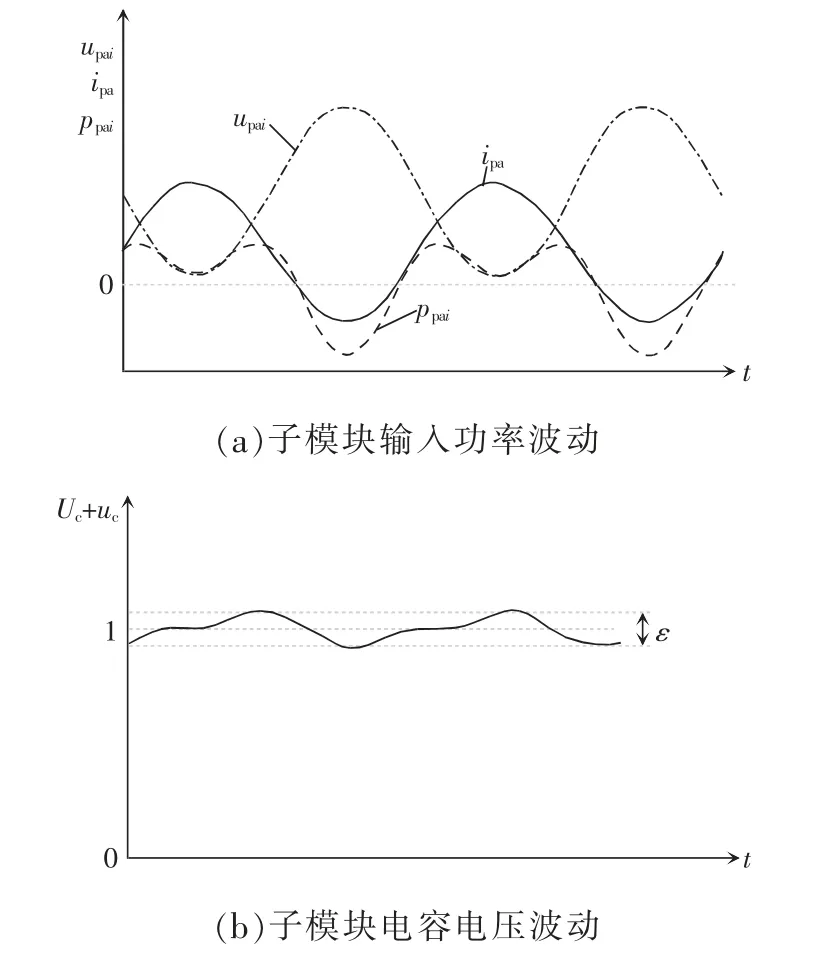
图2 子模块功率与电压波动Fig.2 Submodule power and voltage fluctuation

每个子模块可以看作是一个二端口网络。如果忽略二端口网络内部的能量损耗，那么输入到子模块的能量全部被电容C 吸收。则电容的能量变化为

式中：t0为电容电压等于Uc的初始时刻；t 为任意时刻。相比直流电压和交流电压，桥臂电感两端的电压非常小，可以忽略，因此所有上桥臂电容的能量变化epa为

由于纹波远小于电容电压平均值，交流分量uc的平方项可以忽略，可推得电容电压交流分量为

式中：upa为a 相上桥臂所有子模块的输出电压；ua和ia为分别a 相相电压和相电流；ucom为共模电压；iacir为a 相环流。

定义调制比M 为

定义电容电压波动率ε 为电容电压的交流分量峰峰值ucpp与电容电压直流分量的比值，即

不同方法中，共模电压ucom和环流iacir选取不同，使得电容电压波动率ε 不同，因此子模块电容容值需求不同。

2.1 注入共模电压对电容电压波动的影响

如果只注入三次共模电压抑制环流，则共模电压和环流为

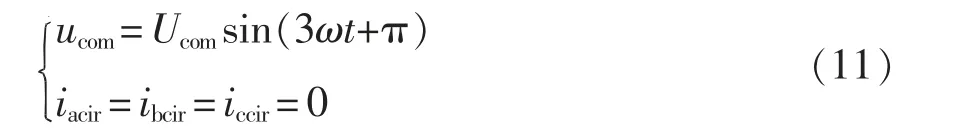
式中：Ucom为共模电压幅值；iacir、ibcir、iccir分别为3 个相单元中的环流。

本文所有电容电压纹波都采用标幺值，即Id=1 p.u.、ω=1 p.u.、C=1 p.u.时电容电压纹波为ucpp。注入三次共模电压会带来2 个影响：①减小子模块电容电压纹波ucpp；②改变最大调制比Mmax，如图3 所示。

图3 注入共模电压对电容电压波动的影响Fig.3 Effect of common-mode voltage injection on capacitor voltage fluctuation

由图3 可见，电容电压纹波随共模电压幅值的增大而减小的速度非常缓慢，如图3（a）中实线所示，因此当调制比不改变时，仅改变共模电压幅值对电容电压纹波的影响非常小；最大调制比随共模电压幅值先增大后减小，当注入的共模电压幅值为交流电压幅值的1/6 时，理论最大调制比达到最大值约1.15，如图3（a）中虚线所示。在直流侧电压和电流不变的情况下，增大调制比可以使电容电压纹波急剧减小，如图3（b）所示。因此，注入共模电压的意义在于通过增加调制比来间接减小子模块电容电压纹波。三次共模电压的选取原则应为使调制比的取值范围达到最大，即采用三次谐波电压注入调制，此时注入的共模电压为

2.2 注入环流对电容电压波动的影响

如果采用正弦波调制，只注入二次环流时，共模电压和环流分别为

式中，I2为二次环流幅值。

在4 种典型调制比下电容电压纹波与二次环流幅值的关系如图4 所示。如果不对环流进行控制，I2将会为负值，其幅值大小取决于电路元件参数，桥臂电感越大环流幅值越小，但只要I2为负值，就会使电容电压纹波比环流为0 时的要大。采用常规抑制环流方法时，I2=0。现有环流注入方法为消除电容电压脉动的二倍频分量时，I2=Id/3。在相同调制比下，相比常规抑制环流方法，现有注入方法可以进一步减小电容电压波动。当调制比升高后，常规抑制环流方法和现有环流注入方法的子模块电容电压纹波都减小。

图4 电容电压纹波与注入二次环流幅值的关系Fig.4 Relationship between capacitor voltage ripple and injected second-order circulating current amplitude

2.3 同时注入共模电压和环流对电容电压波动的影响

如果采用三次谐波电压注入调制，注入二次环流时，共模电压和环流分别为

在4 种典型调制比下电容电压纹波与二次环流幅值的关系如图4（b）所示。注入三次谐波后，调制比的取值范围提高了0.15，常规抑制环流方法和现有环流注入方法的子模块电容电压纹波都比正弦波调制时更小。可以看出，在每一种调制比下，随着注入二次环流幅值的变化，电容电压纹波存在最低点。对于每一种调制比，都存在一种环流注入方式可以使电容电压纹波达到最小，而且随着调制比的升高，电容电压纹波最低点对应的二次环流幅值减小，这是仅考虑二次环流且a 相二次环流的相位与相电流相差π/2 的情况。

3 子模块电容优化方法

3.1 容值优化方法

为了取得最大调制比，采用三次谐波电压注入调制，则上桥臂电压upa和下桥臂电压una可以表示为

3 个相单元中的环流分别为iacir、ibcir、iccir，则上桥臂电流ipa和下桥臂电流ina可以表示为

环流仅在MMC 的3 个相单元内部流通，不流向交、直流侧，仅包含偶次谐波分量，其中6k+2（k=0，1，2，…）次谐波为负序，6k+4 次谐波为正序，6k+6 次谐波为零序。二次环流和四次环流对子模块电容电压波动的影响较大，其他高次环流对子模块电容电压波动的影响较小，因此本文只考虑二次环流和四次环流。

首先，假设只注入的是二次环流，设幅值为I2，a 相相位为θ2，则可表示为

当M=1.1 时，电容电压纹波与二次环流的幅值和相位的关系如图5（a）所示。由图可见，对于任意的二次环流幅值，当且仅当相位为-π/2 时，电容电压纹波取得最小值。换言之，电容电压纹波最小值点一定落在θ2=-π/2 这条线上。因此，当仅注入二次环流时，应取I2=0.43 p.u.，θ2=-π/2。

现在，假设同时注入二次和四次环流，设二次环流的幅值为0.43Id，a 相相位为-π/2；四次环流的幅值为I4，a 相相位为θ4，则有

电容电压纹波与四次环流幅值和相位的关系如图5（b）所示。可见，对于任意的四次环流幅值，电容电压纹波最小值点落在θ4=-π/2 这条线上。由此推断，同时注入二、四次环流时，电容电压纹波的最小值一定在θ2=-π/2、θ4=-π/2 时取得。

图5 电容电压纹波与环流幅值和相位的关系Fig.5 Relationships between capacitor voltage ripple and the amplitude and phase of circulating current

最终，设注入的环流为

定义二次环流注入比为x，四次环流注入比为y，分别表示为

如果忽略变换器的能量损耗,则交流相电流幅值与直流母线电流的关系为

共模电压和环流的注入方式如图6 所示。

图6 注入方式Fig.6 Injection modes

电容电压交流分量的表达式为

电容电压纹波与二次环流注入比和四次环流注入比之间的关系可根据式（22）得出。其中，电容电压纹波与直流母线电流成正比，与交流侧频率和子模块电容容值成反比。因此，本文更加关注调制比、二次环流注入比、四次环流注入比与电容电压纹波之间的关系。在特定的应用场合中，调制比通常是固定的。对于给定的一组交流频率、调制比、直流母线电流和子模块电容容值，电容电压纹波仅与二次环流注入比x 和四次环流注入比y 有关。为了获得最小的电压纹波，应选择适当的x 和y 来使电容电压纹波最小化。

在5 种典型调制比下，绘制了电容电压纹波与二次环流注入比和四次环流注入比的关系曲面，如图7 所示，曲面的最低点表示子模块电容电压纹波最小值点。可见，当M 为1.10、x 和y 分别为0.44 和0.07 时，电容电压纹波达到最小值0.112 7。因此，应取M=1.10，x=0.44，y=0.07。

图7 不同调制比下电容电压纹波与注入比的关系Fig.7 Relationships between capacitor voltage ripple and injection index at different modulation indexes

3 种不同方法的对比结果如图8 所示，图中，常规方法指不注入共模电压且抑制环流，调制比取典型值0.9；现有方法指采用三次谐波电压注入调制，注入二次环流消除电容电压脉动的二倍频分量，调制比取典型值1.05。

3.2 采用容值优化方法下的损耗分析

由于开关频率较低，开关管导通损耗是变换器损耗的主要组成部分。根据文献[16]的计算方法，每个半桥子模块的导通损耗为

式中：U0和R0分别为IGBT 的等效开路电压和内阻，主要由所选用IGBT 的特性决定；Iavr为桥臂电流绝对值的平均值；Irms为桥臂电流的均方根值。Iavr和Irms分别表示为

因此，变换器的整体导通损耗标么值ηloss为

MMC 模型采用直流母线电压9 000 V、直流母线电流150 A、每个桥臂有6 个子模块，同时IGBT模块采用英飞凌FF450R33T3E3 进行损耗计算，取U0=1.52 V、R0=3.13 mΩ。通过计算式（25），得到导通损耗ηloss与注入比的关系，如图9（a）所示。由图可见，环流为0 时损耗并不是最小的，所提方法虽然注入了环流，但损耗更小。这是由于抑制环流时桥臂电流为直流分量叠加一次分量，采用本文所提方法桥臂电流为直流分量叠加一次、二次和四次分量，可以证明，如果二次和四次分量选取合适，桥臂电流绝对值的平均值比二次和四次分量为0 时更小，而桥臂电流绝对值的平均值与导通损耗直接相关。不同方法的导通损耗对比如图8（b）所示。

图8 不同方法的对比结果Fig.8 Comparison results among different methods

图9 导通损耗和开关管电流应力与注入比的关系Fig.9 Relationship between conduction loss,transistor current stress,and injection index

3.3 采用容值优化方法下的开关管电流应力分析

开关管电流应力以直流母线电流为标准标幺化。开关管电流应力与注入比的关系如图9（b）所示。不同方法的开关管电流应力对比如图8（c）所示。在抑制环流方法中，开关管电流应力为1.074 倍的直流母线电流。本文所提方法的电流应力比抑制环流方法的提高了22%。

3.4 容值优化环流控制方案

系统的环流控制方案如图10 所示。调制波是输出电流控制环路输出、环流控制环路输出和直流分量的叠加。

图中：ipa、ina分别是a 相上桥臂、下桥臂电流，它们相减得到a 相交流侧相电流ia；ipb、inb分别是b 相上桥臂、下桥臂电流，它们相减得到b 相交流侧相电流ib；ipc、inc分别是c 相上桥臂、下桥臂电流，它们相减得到c 相交流侧相电流ic；id、iq分别是ia、ib和ic经过dq 变换得到的d 轴电流值和q 轴电流值；分别是d 轴电流和q 轴电流的参考值，由系统的有功功率和无功功率计算得到；Ud、Uq分别是三相电压经过dq 变换得到的d 轴电压值和q 轴电压值；分别是经三次谐波注入后的三相控制信号；分别是a 相、b 相和c 相的环流参考值，该环流参考值由第3.1 节计算得到的二次环流和四次环流组成；分别是a 相、b相和c 相环流参考值与实际值相减后经过PR 控制器的输出信号；Ud是直流母线电压；upa、una分别是a相上桥臂、下桥臂的调制电压；upb、unb分别是b 相上桥臂、下桥臂的调制电压；upc、unc分别是c 相上桥臂、下桥臂的调制电压。upa和una满足

图10 环流控制方案Fig.10 Control scheme of circulating current

4 仿真验证

为了验证所提方法，本文建立了基于MMC 系统的并网逆变器模型。直流侧为直流电压源，交流侧为三相电压源，采用定输出电流控制策略。在Matlab/Simulink 中建立了并网MMC 模型，参数如表1 所示。本文所提方法与常规方法（不注入共模电压且抑制环流）的仿真结果如图11 所示。

图11 Matlab/Simulink 仿真结果Fig.11 Matlab/Simulink simulation results

为了进一步验证本文所提方法，在RT-LAB 硬件在环仿真平台上进行了验证，所用MMC 模型参数如表1 所示，考虑了开关管死区时间、采样误差、AD 转换等实际情况。本文所提方法和常规方法的实时仿真结果分别如图12（a）和图12（b）所示。当子模块电容电压波动率都为10%时，采用本文所提方法的子模块电容为0.38 mF，采用常规方法的子模块电容为1.7 mF。可知，本文所提方法的子模块电容容值的需求约为常规方法的22%。

表1 并网MMC 模型的参数Tab.1 Parameters of grid-connected MMC model

图12 RT-LAB 实时仿真结果Fig.12 RT-LAB real-time simulation results

5 结语

为了减小MMC 子模块电容容值，本文提出了一种优化方法。通过注入特定幅值和相位的三次共模电压和二、四次环流，选取最优调制比，对子模块电容电压纹波进行了优化。采用本文所提方法可以使子模块电容容值的需求降低至常规方法的22%，变换器功率损耗降低至常规方法的87%，而开关管电流应力与现有方法相比只增加0.5%。同时需指出，由于本文所提方法在调制比取值较大时需注入的环流成分较小，这样才能降低损耗，因此适用于调制比接近1.1 的场合。