基于残差连接和1D-CNN的滚动轴承故障诊断研究

赵敬娇， 赵志宏,2， 杨绍普,2

(1. 石家庄铁道大学 信息科学与技术学院，石家庄 050043；2. 石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室，石家庄 050043)

随着智能化时代的到来，机械设备作为众多生产领域的关键设备，对于制造业的发展十分关键[1]。旋转机械设备中滚动轴承是十分重要的部件，因长期工作在恶劣的环境下而极易出现损伤。相关资料显示，旋转机械故障40%以上的原因是由轴承故障引起的[2]。轴承一旦出现故障，如果未能及时发现可能使整个设备停摆，甚至导致重大经济损失和安全事故，为此对滚动轴承故障诊断方法的研究十分必要。

轴承故障诊断的研究至今已有多种方法，如基于频谱分析、冲击脉冲的故障诊断等[3-4]。随着机器学习的发展，越来越多的专家和学者将目光放在智能诊断上，通过不同手段进行特征提取，再用一定方法进行状态识别。深度学习是机器学习的一个重要分支，而近几年由于其在计算机视觉、自然语言处理等领域的优异成就，逐渐被应用到更多的领域解决不同的问题。在故障诊断方面，Tamilselvan等[5]采用深度信念网络，对发动机振动信号及其故障模式建模，实现了飞机发动机故障的诊断，识别正确率达到 92%以上。杨宇等[6]以经验模态分解的方法得到本征模态函数(intrinsic mode functions，IMF)分量，再提取部分分量能量特征参数输入BP(back propagation)网络中进行分类。杜小磊等[7]用多个小波卷积自编码器堆叠后提取故障特征，输入LSTM(long short-term memory)网络后进行分类。众多研究表明，通过建立多层神经网络进行轴承故障诊断是可行并且有效的方法。

卷积神经网络(convolutional neural network，CNN)[8]是深度学习中的一种具有表征学习能力的前馈神经网络，被广泛应用于机器视觉领域。李恒等[9]用短时傅里叶变化对振动信号进行处理后输出到卷积神经网络中，经过网络训练最后进行分类得到故障类型。Pan等[10]建立基于LSTM和CNN的模型进行轴承的故障诊断，取得较好的试验结果。张立智等[11]提出用卷积降噪自编码实现特征提取，用CNN进行模式识别的轴承故障诊断方法。以上方法均取得了较好的诊断结果，但是有些并没有发挥CNN强大的特征提取能力，或是由于维度变换损失了部分时序信息，或是只使用了浅层的网络结构。一般来说，网络越深表达能力越强，在处理大量数据时能够取得更好的效果，而残差网络在精度和收敛等方面都展现出了很好的特性[12]。因此本文提出一种基于残差连接和一维卷积神经网络(one-dimensional convolutional neural network，1D-CNN)的深层故障诊断模型，通过多层1D-CNN提取不同层次特征，通过残差连接将深层特征信息与浅层特征信息结合，使网络学习到更多的轴承故障特征信息。

1 一维卷积神经网络

1.1 一维卷积网络

CNN具有局部连接和权值共享的特性[13]，参数共享能够有效削弱过拟合的问题，稀疏连接能够让网络学习局部特征。一维卷积神经网络[14]是运用一维卷积对一维时序序列进行特征提取的卷积神经网络，能够保证在不损失时序特征的同时提取局部特征，对于轴承振动信号这样的周期的时间序列分析是非常有效的。

卷积神经网络通常包括以下三层：①卷积层，通过卷积核对输入的特征进行扫描，在“感受野”内对输入特征进行矩阵运算并叠加偏差量[15]，从而实现特征提取的作用；②池化层，池化操作就是利用一个矩阵窗口在张量上进行扫描，将最大值或者平均值作为特征的输出，以减少参数数量和计算量；③全连接层，对提取的特征进行非线性组合输出到其他全连接层。卷积层和池化层能够达到自动提取数据局部特征的目的，而全连接层能够实现特征学习。

一维卷积公式为

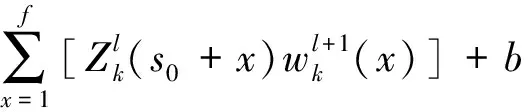
(1)

最大池化公式为

(2)

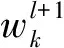
1.2 残差连接

已有研究发现构建的网络越深，越容易出现梯度消失、网络过拟合的现象，残差连接能有效解决网络退化和梯度消失的问题。残差连接的思想源于LSTM的门控思想，将输入做非线性变换，再和输入进行线性叠加输出[16-17]，如图1所示。

图1 残差块Fig.1 Residual block

网络的一层通常可以看作y=H(x)，而残差网络的残差块的输出上可以表示为H(x)=x+F(x)，也就是说残差为预测值H(x)与观测值y=x的差值，即F(x)=H(x)-x。残差网络的学习目标由学习H(x)变为学习残差F(x)，网络只需要学习输入、输出差别的部分，从而降低学习的难度。

残差块的输出公式为

xl+1=xl+F(xl,wl)

(3)

式中：xl+1为第l+1层的输出；xl为第l层的输入；F(xl,wl)为第l层的残差。

跳跃连接能够在某个网络层激活后迅速反馈给另外一层甚至更深层，从而避免传统卷积层和全连接层在信息传递时的信息丢失和损耗。利用跳跃连接可以构建深层网络来训练更深的网络，可在确保网络参数不变、计算量不增加的同时，保证网络有足够的能力去处理更加复杂的数据。

1.3 批量标准化

在深度网络中，输入数据的均值和标准差会随着网络层数的增加在逐级传递中发生改变，即协变漂移现象[18]，协变漂移也是导致深度网络出现梯度消失的原因之一。批量标准化(batch normalization，BN)以引入部分额外学习参数为代价解决了此类问题：首先将特征标准化，然后标准化的特征会被2个线性参数放大，成为新的输入，BN参数在学习过程中不断更新。

卷积神经网络中的BN参数与卷积核参数具有相同的性质，即特征图中同一个通道的像素共享一组BN参数[19]。此外，偏差项的功能可由BN参数代替，使用BN层时卷积层不必添加偏差项。通过加入BN层能够：改善流经网络的梯度，允许更大的学习率，大幅提高训练速度；减少对初始化的强烈依赖；改善正则化策略，并且减少了对Dropout的需求。

2 故障诊断模型设计

在实际的轴承故障诊断中，振动信号数据量巨大，网络单纯采用CNN会耗费很大的时间，并且深层网络也会导致梯度消失问题出现和泛化性能的下降。利用批量标准化技术的BN层代替部分池化层，能在一定程度上解决梯度消失问题；添加Dropout层能够有效减小过拟合问题[20]，使模型的诊断精度提升，提高泛化能力；Softmax层是进行分类的常用网络，能够输出概率分布图；最终根据概率分布确定轴承信号的振动信号类型，并根据数据标签的诊断结果输出正确率。

本文构建的轴承故障诊断模型，如图2所示。模型主要包括输入层、特征提取层以及输出层三部分。其过程为：①一维滚动轴承振动数据输入网络输入层。②特征提取部分。首先对输入进行一次卷积，然后将此次卷积输出分成两部分：一部分保存为identity；另一部分继续输入到残差块部分。残差块部分由3个BN层和卷积(Conv1D)层组成，经过其中的三次卷积的结果与保存的identity相加，得到残差输出。运用2个残差块并进行两次跳跃连接构成整个残差连接部分。得到的结果再经过1层BN层、Conv1D层和最大池化层，最终得到提取的特征。③将池化层得到的输出经过扁平层“压平”，再添加Dropout层防止过拟合，最终通过Softmax层进行分类。

图2 轴承故障诊断模型图Fig.2 Bearing fault diagnosis model

3 试 验

3.1 试验数据

试验数据采用美国凯斯西储大学负载为0，转速为1 797 r/min的6205-2RS JEM SKF深沟球型轴承试验台数据。利用电火花加工技术对轴承进行加工，以48 kHz的频率采样，人为地在内圈、外圈以及滚动体加工出损伤直径分别为0.177 8 mm，0.355 6 mm，0.533 4 mm的单点故障。本文数据集共7 000个，按70%，20%和10%的比例划分为训练集、测试集和验证集。数据集共包含10类样本、9种类型的故障和1类正常数据，将标签数字从0～9按顺序分别命名为“B007”，“B014”，“B021”，“IR007”，“IR014”等，详细数据及标签如表1所示。

3.2 试验设置

本试验的批大小设为128，学习率初始值为0.000 5，每隔50次的迭代降低为原来的20%，振动信号的样本输入长度为1 024。试验共在训练集上迭代300次，最终用测试集输入到模型得到准确率。

表1 试验数据集Tab.1 Experimental dataset

网络结构设置如下：第一层卷积层滤波器个数为64，卷积长度为2，卷积步长为1；残差块的每个BN层后的卷积层均设为由64个2*1的卷积核的滤波器组成的网络层；再经过一个BN层、卷积层，卷积层由32个2*1的卷积核的滤波器组成。以上网络层的激活函数均选用“relu”函数，以及“same”的填充方式；最大池化层的池化块尺寸为4，步长为4，填充方式为“valid”。经过扁平层和一个抛弃率为0.5的Dropout层，最后以“Softmax”为激活函数的Dense层做分类。

3.3 试验结果及分析

轴承故障诊断的评价指标有准确率、损失率、召回率和F1值等，其中准确率和损失率是判断模型优异的重要标准。经过多次试验结果如图3所示，准确率和损失率分别如图3(a)和图3(b)所示，由于学习率设置，模型在前50次的学习速度很快，但波动较大，50次之后准确率缓慢变化，最终保持稳定。本模型在数据集的1 000个测试集上的总准确率达到98.6%，损失率为5.0%。图3(c)为混淆矩阵表示的结果输出，其中0.533 4 mm的滚动体故障、0.177 8 mm的外圈故障和0.533 4 mm的外圈故障检测出现错误，其他故障均能有效识别。

图3 试验结果Fig.3 Experimental results

3.3.1 不同残差模型结构对比

本文选用不同残差块以及跳跃连接设计建立多个故障诊断模型，在相同参数的设置情况下，试验中多个模型只改变图2中残差块的结构，其他网络层不变。残差块设计如图4所示，残差部分设置如下：

(1) 将图2模型中的残差块部分换为2个BN层与Conv1D层，不加跳跃连接，如图4(a)所示，模型命名为2-C-1；在相同BN层和Conv1D层的情况下，加1个跳跃连接，如图4(b)所示，模型命名为2-R-1。

(2) 残差块部分换为3个BN层与Conv1D层，不加跳跃连接，如图4(c)所示，模型命名为3-C-1；在相同BN层和Conv1D层的情况下，加1个跳跃连接，如图4(d)所示，模型命名为3-R-1。

(3) 残差块部分换为4个BN层与Conv1D层，不加跳跃连接，如图4(e)所示，模型命名为2-C-2；在相同的BN层和Conv1D层的情况下，加2个跳跃连接，如图4(f)所示，模型命名为2-R-2。

(4) 残差块部分换为6个BN层与Conv1D层，不加跳跃连接，如图4(g)所示，模型命名为3-C-2；在相同的BN层和Conv1D层的情况下，加2个跳跃连接，如图4(h)所示，模型命名为3-R-2。

图4 残差块结构Fig.4 Residual block structure

不同残差模型结构的故障诊断试验结果，如表2所示。在相同超参数设置情况下，3-R-2模型的残差设计的诊断效果最佳。同时，本文尝试比3-R-2模型更深的结构进行试验，诊断效果差异并不大。由表2可知：①使用残差连接的模型的故障诊断效果有了一定的提升，这是由于残差连接能够将浅层特征和深层特征融合作为特征输出，比起单一的深层特征更有效；②模型网络层数增加，故障诊断结果有一定的提升，这是因为模型加深，能够提取轴承故障信号的一些深层特征信息。但并不是模型越深，故障诊断效果越好，网络层数过多会出现学习参数的成倍增长和过拟合严重现象。因此，基于残差连接的1D-CNN模型能够有效判断各故障类型，并且在此8个模型中，最优模型为本文图2所采用的滚动轴承故障诊断模型结构。

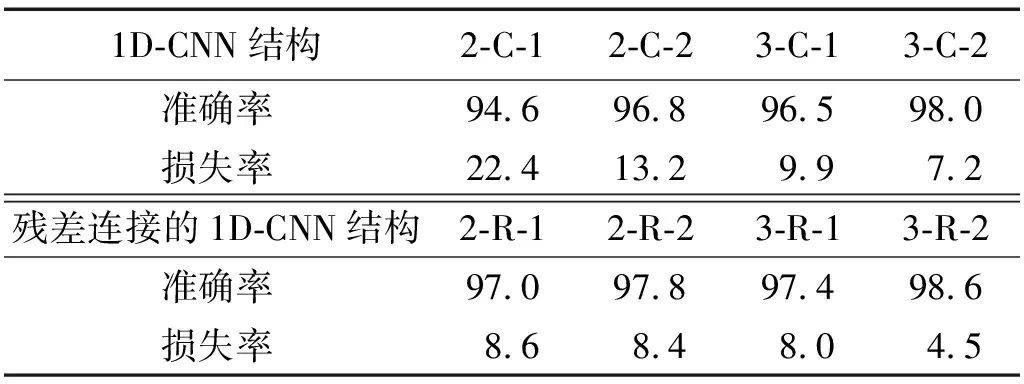
表2 不同网络结构的诊断准确率和损失率Tab.2 Accuracy and loss rate of different network structures %

3.3.2 不同参数取值对试验结果的影响

轴承故障诊断模型的参数有学习率、批大小、滤波器个数等，这些参数的选择会引起诊断效果的不同。本文对学习率、滤波器个数选择进行了对比试验。

(1) 学习率。如果学习率设置过大，可能导致参数更新幅度非常大，网络难以收敛，使损失值过大；如果学习率设置太小，则网络需要训练更长时间才能达到稳定，或者只收敛到局部最优点，无法达到全局最优。

本文选择先使用0.000 5的大学习率快速学习特征，使学习率快速提升。但是大学习率情况下准确率波动大，因此在每50次的训练后改变学习率，变为原来的20%，使学习率平稳提升。经过多次试验证明此方法较为有效。

(2) 滤波器个数。滤波器是CNN网络的一个重要参数，数量多了会拖慢训练且易过拟合，少了会丢失特征，特征学习不好。因此本文在不同滤波器个数下进行了对比试验，根据试验结果选择适合本文模型的滤波器参数设置。模型在不同滤波器数量下的准确率，如表3所示，滤波器个数为32和64的诊断效果较好，但滤波器个数为64的情况下损失率更小，准确率更高，因此本文选用滤波器个数为64。

表3 不同滤波器数量下模型的准确率和损失率Tab.3 Accuracy and loss rate of different filter number

3.3.3 可视化分析

采用t-SNE(t-distributed stochastic neighbor embedding)算法[21]提取各层输出向量的前二维以显示模型不同网络层特征提取的结果。原始输入信号以及其经过部分网络层的特征图，如图5所示。图5(a)为原始输入信号的t-SNE可视化图，可以看到原始信号比较杂乱，各类数据相互混杂，难以区分。经过第1个残差块的卷积层后的t-SNE可视化图，如图5(b)所示，标签5的数据被分类出来，其余部分的各类样本并没有聚拢，而是十分混乱地聚在一起。经过第1个残差块的第3个卷积层后的t-SNE可视化图，如图5(c)所示，虽然各类并没有完全分散，但是聚集的不同种类的数据较之前分散，并且各类数据成聚集的趋势，其中标签9和标签5已经完全聚集，标签0、标签1、标签2、标签4、标签6、标签8等成聚集的形式汇聚。试验结果表明，模型各层能提取故障特征用于分类，最终分类准确率在98%以上。

图5 原始信号及网络层输出可视化图Fig.5 Visualization diagram of original signal and different network layers

4 结 论

对于滚动轴承的故障诊断，本文提出了基于残差连接的深层1D-CNN模型，解决了传统故障诊断方法人工提取特征的不足。试验结果表明，本文提出的模型能够根据输入的轴承振动信号有效识别滚动轴承故障状态。

(1) 基于残差连接的1D-CNN能够提取轴承故障特征，轴承故障识别率较高。

(2) 与无残差连接的卷积神经网络相比，使用残差连接的1D-CNN能够提取多层次故障特征，诊断效果更好。

(3) 深层网络模型较浅层网络表达能力更强，在“大数据”时代，本文提出的深层故障诊断模型具有一定的应用价值。

故障诊断模型中各参数的取值会不同程度地影响诊断效果，而依据人工调参十分繁杂。因此，本文下一步的研究重点在参数选择算法方面，并建立自适应的故障诊断模型。