基于数字图像相关方法的薄板结构振动功率流可视化

朱海华， 孟 帆， 宋汉文

(同济大学 航空航天与力学学院，上海 200092)

本文对结构振强的实验研究基于数字图像相关方法(digital image correlation，DIC)，作为一种非接触式的全场测量手段，数字图像相关方法可对被测结构进行空间高分辨率的测量。因数字图像相关方法的本底噪声对于空间微分计算的影响较大，故有限差分方法不可取用。而基于波数域方法的空间微分计算，因非周期边界条件带来的吉伯斯效应影响极大，目前相关实验研究大多集中于处理四边夹支薄板。Arruda[26]提出一种退化傅里叶变换的方法以减小波数域谱的高频成分，可获得较好的微分计算结果。这种方法通过样条外插对四边固支或简支板的位移场进行插值处理，使其满足周期边界条件，但是这种算法依赖于插值范围及精度，故计算结果的精确性较难把握。

本文工作将基于数字图像相关方法获得薄板结构全场运动数据，并通过傅里叶级数连续延拓空间信号以消除吉伯斯效应所引入的高频影响，提高空间微分计算精度，进一步得到振动功率流。通过对结构振强及其散度场的可视化，可实现对能量传递路径及振源识别的直观表征，为下一步的结构振动与噪声控制奠定基础。

1 基本理论

1.1 结构振强

在薄板结构中，功率流由板内广义力与其相对应的速度作用产生，在克希霍夫薄板的假设下，弯曲波对板振动能量的贡献最大[27]。图1所示为各向同性的均质薄板在纯弯曲状态下的板单元所受内力状态，单元所受的主要内力为剪力、弯矩及扭矩，结构振强定义为

(1)

(2)

式(1)和式(2)表示单位时间内，x，y方向单位截面的功率流。式中：Mx，My为弯矩，由法向应力合成；Mxy，Myx为扭矩，由面内切应力合成；Qx，Qy为剪力，由横向切应力合成。各内力作用方向上对应的广义位移分别为转角θx，θy及横向位移w。根据克希霍夫假设，式(1)和式(2)中各内力及速度分量可表达为关于挠度的物理量，则式(1)和式(2)可表示为

(3)

(4)

式中， 〈〉t为时间上的平均量，以此表示单位时间内板单元内流过的能量即功率。

图1 板单元受力状态Fig.1 Generalized forces per unit in plate element

对结构振强进行流场可视化表达，流线上各点的切线方向与功率流矢量方向一致，因此其数学表达式为[28]

(5)

(6)

而对于板单元这样的二维结构而言，式(6)可以简化为如下形式以刻画矢量场

(7)

通过流线可视化技术，可直观表征振动能量传递的传递方式。若结构中包含能量的注入区域，则通过对式(8)所示结构振强的散度场的可视化表达，可明显直观地观察到振源位置。

(8)

1.2 基于波数域的空间微分及滤波方法

由式(3)和式(4)可知，除材料的力学性质及薄板厚度外，结构振强的计算依赖于板的挠度和速度及其对空间的高阶微分，若数值误差较大，则会严重影响功率流及振源位置的可视化，故对于数值微分计算的精确性尤为重要。通过对二维场进行空间傅里叶变换(spatial fourier transform, SFT)，基于波数域计算数值微分的方法，具有全局性、精确性及克服噪声影响等优势，高阶微分可表示为

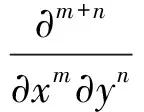
(9)

W(kx,ky)=F{w(x,y)}

(10)

式中：F为空间傅里叶变换算子；(kx,ky)为波数域坐标；(x,y)为空间域坐标；m，n分别为在x，y上的微分阶数；W为空间二维信号w的空间傅里叶变换结果； j为虚数单位。

观察式(9)可知，基于波数域的数值微分计算中，波数域中的高频成分会在高阶导数的计算中被急剧放大，从而极大影响计算结果的准确性。而对于DIC实验而言，实验所得位移场在波数域中所对应的高频分量由两部分原因造成： 一方面是边界条件的非周期性导致的吉伯斯效应，从而在波数域中引入高频成分；另一方面是位移场中分布的空间噪声。本节提出二维傅里叶连续延拓的方法构造空间周期信号，消除吉伯斯效应的影响；再针对空间去噪，引入波数域低通滤波。

1.2.1 傅里叶连续延拓

对于薄板结构实验所测实际位移或速度场，在边界处并不满足周期性要求，存在吉伯斯效应，由此引入的高频成分会在微分计算中导致很严重的误差。本文改进文献中信号延拓的方法[29]，使其适用于二维信号的处理，通过傅里叶级数拟合的方法，延拓原空间信号使其满足周期边界条件，消除吉伯斯效应。其数学表达式为

(11)

bx及by表示在x和y方向上的延拓周期，通常选为原信号区间的两倍。即原信号区间为[0,ax]×[0,ay]时，则延拓后信号的区间为[0,bx]×[0,by]，其中bx=2ax，by=2ay。当My为偶数时，kn=n-My/2，My为奇数时，kn=n-(My+1)/2;当Mx为偶数时，km=m-Mx/2，Mx为奇数时，km=m-(Mx+1)/2。未知系数Amn可通过原信号得到最小二乘意义下的解

(12)

xp和yq分别表示x，y方向上的第p个、第q个坐标，w(xp,yq)表示区间[0,ax]×[0,ay]的原信号。将式(13)以矩阵形式表示，w(xp,yq)及Amn重构为一维向量

(13)

(14)

(15)

则上式表示为求解方程[B]{α}≈{w}在区间[0,ax]×[0,ay]上的解。通过对[B]进行SVD分解，则系数矩阵的解为

(16)

图2所示为函数f(x,y)=0.1ex+y在区间[0,1]×[0,1]的图形，经过傅里叶连续延拓至区间[0,2]×[0,2]构成满足周期边界条件的二维信号，如图3所示。

图2 f(x,y)=0.1ex+y在区间[0,1]×[0,1]上初始信号Fig.2 Initial signal in[0,1]×[0,1]

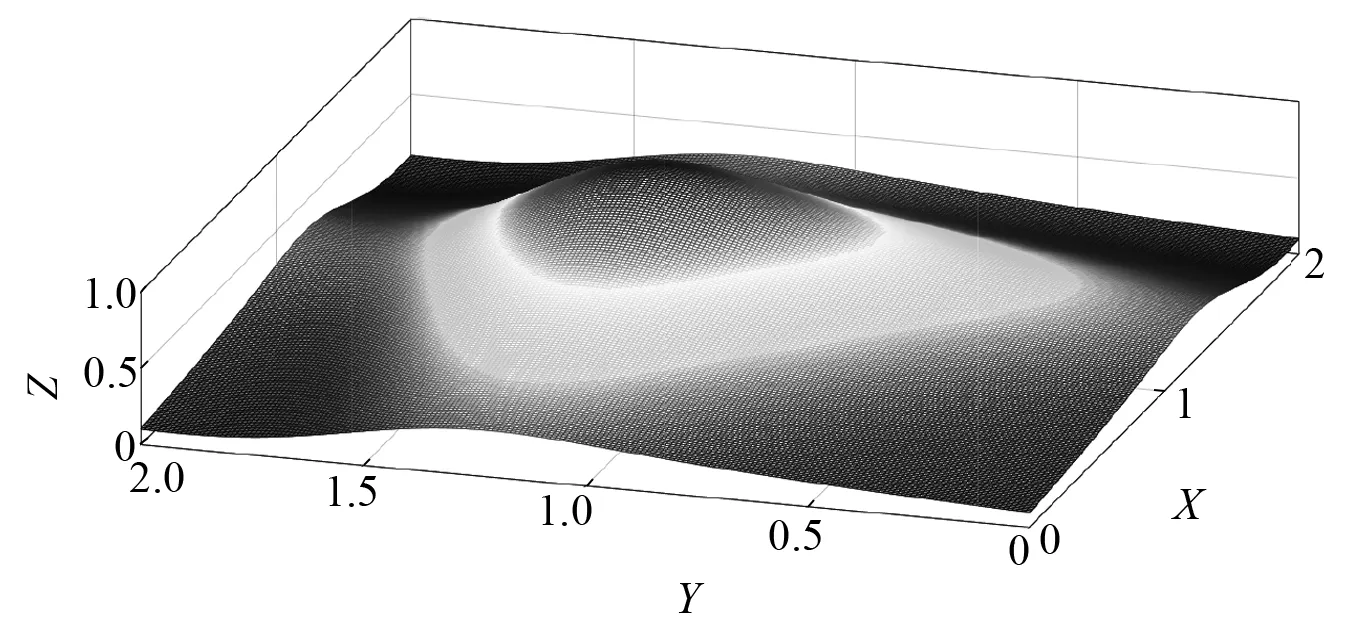
图3 经延拓至[0,2]×[0,2]的周期信号Fig.3 Periodic signal after continuation in the interval[0,2]×[0,2]

1.2.2 波数域低通滤波

去除吉伯斯效应所引入的高频影响后，再针对位移场中的空间噪声引入的高频分量进行剔除。与有限差分方法相比，对空间信号进行低通滤波再计算空间导数，波数域微分方法的精确性更不易受噪声影响。本文采用Li等改进的波数域滤波方法，滤波效果由截止波数kc及参数s控制。窗函数表达式为

(17)

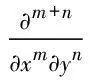
(18)

1.3 三维数字图像相关方法(3D-DIC)

数字图像相关方法作为一种非接触式的光学测量方法，可获得被测结构的三维全场运动信息。数字图像相关方法首先在被测结构表面进行预处理，形成高对比度的二维随机散斑。利用双目高速摄像机记录结构运动过程的系列图像信息，并将图像划分为若干虚拟子集(见图4)，通过对每个子集的追踪可得到结构整体的二维运动。散斑的随机性保障了子集匹配的唯一性，最后基于双目视觉的三角测量原理(见图5)，将像素坐标重构为三维世界坐标，获得结构实际运动信息。

图4 散斑子集示意图Fig.4 Diagram of speckle subset and substep

图5 视觉测量原理示意图Fig.5 Principle of vision measurement

近年来，随着摄像机性能的提高，以及计算机存储能力的飞跃发展，国内外已有一定量的研究将数字图像相关方法应用到结构的动力学测试中。文献[30]利用数字图像相关方法提取干燥箱面板的前三阶振型，并与有限元计算结果对比，阐述了此方法在模态分析中的适用性。Reu等[31]使用数字图像相关方法及激光多普勒测量仪分别对一块铝板进行模态分析，对比不同方法所辨识得到的模态参数，证明了数字图像相关方法在振动测试中的优越性。Rizo-Patron等[32]利用数字图像相关方法对直升机旋翼叶片进行了工况模态分析，得到叶片模型在不同转速下的前三阶固有频率。

目前数字图像相关方法在结构振动测试中已有一定数量的研究工作，其有效性及精确性等优点已得到证实。而基于此方法对结构振动能量相关的研究甚少，本文工作主要利用其非接触式、空间高分辨率的全场测量优势，展开对薄板结构功率流可视化的研究，计算流程如图6所示。首先通过数字图像相关方法获得结构表面振动过程的全场分布，通过傅里叶连续延拓重构为周期边界信号，再进行波数域上的滤波以及微分计算，最后得到空间微分结果，进一步计算各方向上的振动功率流。

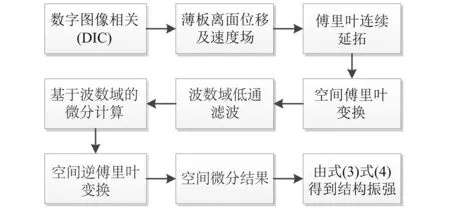
图6 数据处理流程图Fig.6 Flow chart of data processing

2 实验研究

本文采用DIC展开振动功率流的实验研究，测量并计算得到了薄板结构在不同激励频率下的工作变形形状(operational deflection shape, ODS)以及结构振强。实验对象为各项同性的复合材料薄板，相关材料参数见表1。薄板通过螺栓与型材框架固定，并将结构利用角钢夹持固定在隔振台上，利用激振器作为激励源。双目摄像机通过同步控制仪外触发拍摄，图像输出到工控机内储存，实验装置如图7所示，其中图7(b)为表面散斑。激励位置离右下角水平距离为75 mm,垂直距离为50 mm，如图7(b)所示。综合考虑视场大小、测点的空间分辨率以及所关心的振动频率，在相机硬件条件的允许下，相机设置及散斑等相关参数见表2。

表1 薄板相关物理参数Tab.1 Physical parameter of plate

图7 实验装置图Fig.7 Diagram of experiment setup

表2 相机及散斑相关参数Tab.2 Parameter of stereo camera and speckle

首先对薄板进行预实验，通过双目相机记录结构在白噪声随机激励下振动过程的图像信息，并通过数字图像相关方法获得实际振动信号，进一步得到结构的前四阶固有频率，如表3所示。

表3 前四阶固有频率Tab.3 First four modal frequency

选取所关心的前四阶频率作为输入频率，对结构进行单频正弦激励，获得各频率下的工作变形形状，如图8所示；以及各频率激励下的ODS在波数域上的频谱图，如图9所示。

因基于数字图像相关方法测量的实验往往在边界处不能获得良好的数据。在舍弃边界值之后，ODS并不满足理想的周期边界条件，故因吉伯斯效应而在空间频谱上引入了高频分量，如图9所示。为消除其在基于波数域的微分计算过程中的影响，采用1.2节所述的傅里叶连续延拓的方法，并联合空间低通滤波。截止波数的选取依据有限元计算的理论结果，因位移场所对应的波数随着振动频率的升高而增大，故在本文所关心的频率范围内，选取有限元计算结果的第四阶振型所对应的最高波数作为截止波数。图10中：图10(a)所示为第四阶计算模态振型；图10(b)和图10(c)为其对应的波数域频谱，可以发现波数分布集中在65 rad/m范围内。故选取65 rad/m作为截止波数，以避免对实验数据的过渡滤波。

图8 不同频率下归一化的ODSFig.8 Operational deflection shape normalized by their respective maximum values

通过图6所述数据处理流程基于波数域计算空间微分，进一步得到结构振强及其散度场，如图11所示。

图11(a)～图11(d)中流线图分别为71.6 Hz，120.8 Hz，167.0 Hz及207.4 Hz激励下的结构振强矢量场，云图表示结构振强所对应的归一化散度场。通过观察图像发现，随着激励频率的升高，功率流的传递路径也愈加复杂，涡流表示能量出现了汇聚。尽管不同激励频率下结构振强的流线图不同，但其对应的散度场大致相同。高亮区域为散度场的极值，即代表能量的注入点。通过与实验中激振器激励点进行对比，振源位置吻合良好。

图9 不同频率下ODS的波数域频谱Fig.9 Wavenumber domain representation of the ODS

图10 截止波数的选取Fig.10 Cut-off wavenumber

3 仿真算例

利用ANSYS对薄板进行建模计算，边界条件设置为四边固支，通过计算模态分析得到前四阶固有频率(见表4)。

采用ANSYS谐响应分析模块计算薄板在关心频率下的内力及速度响应结果，通过MATLAB计算结构振强并得到如图12所示的可视化结果。

表4 前四阶固有频率Tab.4 First four modal frequency

图11 结构振强及其散度场Fig.11 Structural intensity and divergence fields with respect to SI

图12 结构振强及其散度场仿真结果Fig.12 Results of FEM for structural intensity and divergence fields with respect to SI

对比DIC实验与有限元计算结果，前四阶固有频率相差在5%以内，结构振强场的振源位置吻合良好。

4 结 论

本文工作基于视觉测量手段的数字图像相关方法，利用其非接触及空间高分辨率测量的优势，展开对薄板结构振动功率流的可视化研究，得到以下结论：

(1) 通过数字图像相关方法获得了薄板结构前四阶固有频率，以及关注频率下的工作变形形状。

(2) 采用傅里叶连续延拓的信号处理方法，实现了较好的空间微分计算结果，进一步得到了结构振强及其散度场。利用流线可视化技术并结合散度场云图，实现了对结构振动功率流以及振源的可视化。

数字图像相关方法的全场测量优势为实验数据带来丰富测点信息，并且不会改变系统的固有动力学特性，为薄板结构振动功率流的实验研究提供了有效手段。通过对能量传递路径以及振源识别的可视化，为进一步振动控制奠定基础。