摩擦摆式支座对地震时桥上车辆安全性的影响

晋智斌， 何金哲， 曾永平， 董 俊

(1. 西南交通大学 桥梁工程系，成都 610031； 2. 中铁二院工程集团有限公司，成都 610031)

历史上曾屡次发生地震下铁道列车脱轨甚至倾覆的事故。如唐山大地震3列客车4列货车发生部分车辆脱轨或颠覆[1]，日本新泻地震中新干线列车“朱鹮325”号10节车厢有7节脱轨[2]。针对地震下桥上行车安全评价问题，国内外研究者发展了诸多地震-车-桥分析理论。如韩艳等[3-4]对地震作用下列车通过连续梁桥、简支梁桥以及拱桥进行了研究，对桥梁的动力响应和车辆的走行安全进行了评价；林玉森[5]对地震作用下高速铁路桥上列车走行性进行了研究；王少林等[6]通过研究地震作用下高速列车-线路-桥梁系统动力响应得出评判地震作用下高速列车通过桥梁时的行车安全性, 应考虑行车速度的影响；陈令坤等[7]用车-轨-桥耦合模型分析地震下的系统响应；Kawanishi等[8]使用正弦波代替地震波，分析地震作用下车辆的响应；杜宪亭[9]建立了多层次的地震-车-桥分析模型，研究了不同地震动输入模式、地震动空间变异因素、行车速度等对桥梁上运行列车安全性的影响。陈波等[10]采用精细的轮轨关系式建立了地震荷载作用下列车-高架桥系统模型，评估地震作用下的该高架桥列车运行安全性。

我国目前已建成世界最大规模的高铁网络，高速铁路建设正向西部延伸，地震对结构物和列车安全形成巨大的威胁，研究表明桥梁会放大地震PGA(peak ground acceleration)达2倍[11]，地震下桥上脱轨危险性大，且后果严重。

在高烈度地震区，常采用摩擦摆式隔震支座来降低桥梁震害。摩擦摆式支座是通过支座滑块沿弧形滑动面运动的单摆原理来延长结构周期，同时摩擦面提供一定的耗能能力。其构造简单、性能稳定。以往对摩擦摆式桥梁支座的研究主要关注对桥梁本身的减振效果。研究表明，合理的摩擦摆参数设计可显著降低桥墩内力[12]。但摩擦摆式支座会增大桥面振动位移，这对地震下桥上车辆安全产生何种影响尚不明确。本文利用OpenSEES强大的结构动力非线性分析功能，与自主开发的车辆-轨道耦合动力分析程序结合，编制了考虑支座非线性行为的车辆-轨道-桥梁全非线性分析程序。用该程序对比研究了摩擦摆式支座对桥上脱轨危险性的影响。

1 车-轨-桥动力相互作用模型

地震下的桥上脱轨模型分为车辆、轨道和桥梁三部分，其中车辆和轨道采用文献[13]中的模型，即车辆为31自由度的多刚体系统，轨道简化为移动断面模型。桥梁模型在OpenSEES中建立。

1.1 车辆-轨道模型

车辆包括车体、转向架和轮对共7个刚体，如图1所示，车辆以匀速行驶，所有刚体均不计纵向伸缩自由度。因此，车体和各转向架均有5个自由度，即车体有5自由度。车体自由度记作Yc=(yc,zc,φc,θc,ψc)T，转向架自由度记作Yti=(yti,zti,φti,θti,ψti)T。其中：y,z,φ,θ,ψ分别为横移、沉浮、侧滚、点头和摇头运动；下标和c，t分别为车身和转向架。轮对按匀速转动，因此不计其点头自由度，则各轮对有4个自由度，第j(j=1,2,3,4)个轮对的自由度为Ywj=(ywj,zwj,φwj,ψwj)T。四轴车辆共计有31个自由度：YV=(Yc,Yt1,Yt2,Yw1,Yw2,Yw3,Yw4)T。

车体通过二系悬挂与2个转向架相连。二系悬挂的在纵向、横向和垂直方向的刚度为k2x,k2y,k2z，在3个方向的阻尼为c2x,c2y,c2z。一系悬挂的刚度和阻尼分别表示为k1x,k1y,k1z和c1x,c1y,c1z。在车身和每个转向架之间的抗侧滚扭杆的刚度为kR。在地震作用下，车体和构架之间的横向止档会发挥作用，模型中考虑初始间隙为2 cm，刚度为kS的横向止档。

横向止档的力-位移关系，如图2所示。

车辆的动力方程为

(1)

图1 车-轨-桥耦合模型Fig.1 Vehicle-rail-bridge dynamic interaction system model

图2 横向止档的力-位移关系Fig.2 Force-displacement relationship of lateral stopper

(2)

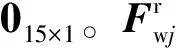
(3)

式中：Hwr,j，Vwr,j和Lwr,j分别为在轮轨接触点处钢轨对车轮的横向、竖向和纵向作用力，如图3所示；上标L和R分别为左侧和右侧钢轨；r为车轮滚动圆半径；b为左右轮轨接触点横向间距之半。车辆为4节编组。车长为(4×26 m=104 m)，已经远大于本研究中的32 m简支梁。

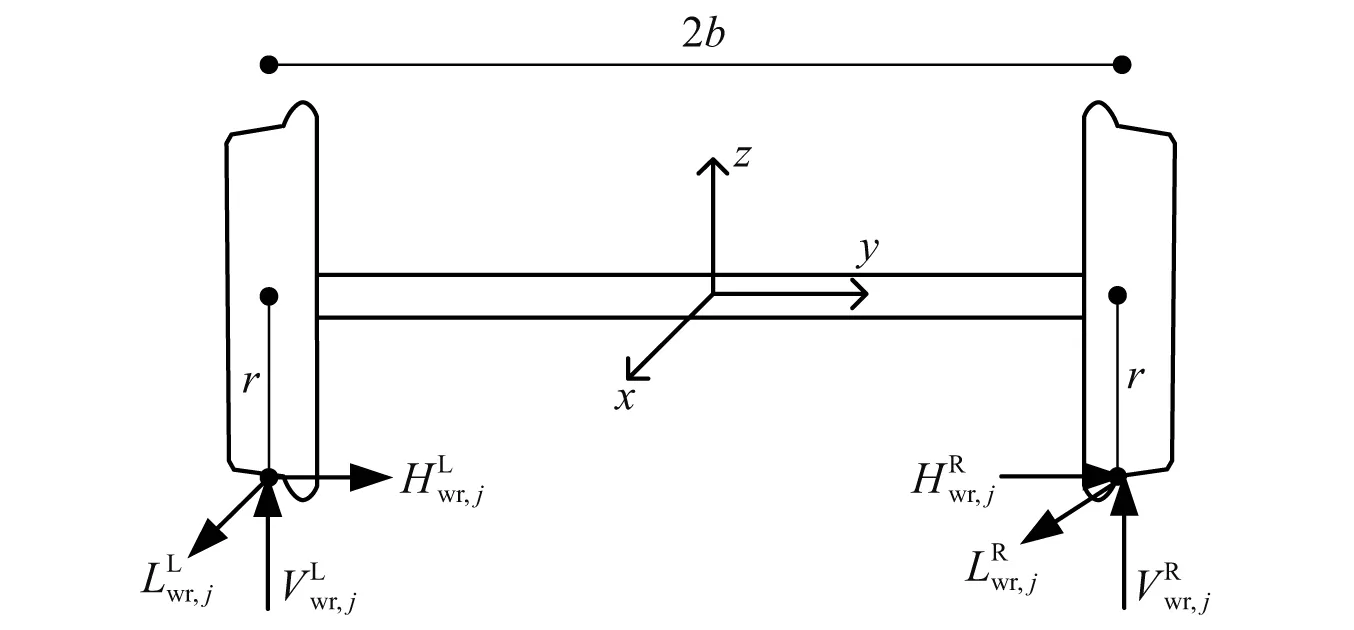
图3 钢轨对轮对的作用力Fig.3 Wheel-rail forces

1.2 钢轨模型

轨道的弹性变形对轮轨冲击起到缓冲作用，在地震车-桥分析中，应计入轨道的作用。本文采用移动轨道截面模型，如图4所示，其实质是用Rayleigh-Ritz法表达钢轨振动方程。根据标准Rayleigh-Ritz 表达式，可推导出钢轨的广义质量、刚度和阻尼。而轨道广义质量、刚度和阻尼组成的轨道振子随车轮沿行进方向移动。

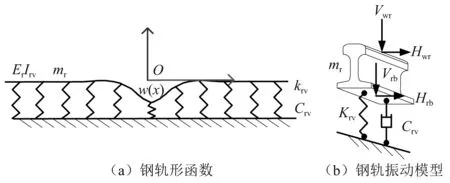
图4 移动轨道模型Fig.4 Moving rail method

Rayleigh-Ritz形状函数取集中力作用下的轨道变形。以轨道竖向变形为例，Rayleigh-Ritz形状函数为

w(x)=e-β|x|[cos(β|x|)+sin(β|x|)]

(4)

以广义位移表达的轨道垂向振动方程为

(5)

式中：qrv(t)为轨道的广义位移；Mrv，Crv和Krv分别为轨道垂向振动的广义质量、阻尼和刚度；Vwr为垂向轮轨力；Vrb为桥梁对轨道的垂向作用力

(6)

式中，Zd为轨道下方桥面的垂向位移。由式(6)可知，车辆8个轮对对应的轨道垂向振动方程为

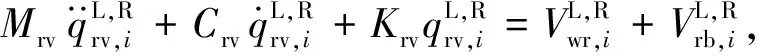
(7)

式中： 下标i为第i个轮对； 上标L和R分别为左轨道和右轨道。

移动轨道的横向运动方程可以以垂向运动相同的方式导出，写为

(8)

式中： 下标h为横向；H为横向力； 其他符号的含义与式(7)相同。式(8)中，桥梁作用在轨道上的横向力Hrb可写为

(9)

式中，Yd为移动轨道下方的横向桥面位移。移动轨道下方的桥面位移可以通过桥面的运动来计算

(10)

式(10)中的几何关系，如图5所示。式中：Yb(xi)，Zb(xi)和θb(xi)分别为桥截面中心的横向、垂直位移和扭转角；xi为桥面上第i个轮对的纵向位置；hr和br分别为轨道底面与梁体质心在垂直和横向的距离。本文中的轨道广义质量、刚度和阻尼取值，如表1所示。

图5 桥面尺寸Fig.5 Dimensions of bridge deck

表1 轨道参数Tab.1 Rail parameters

1.3 摩擦摆式支座

减隔震支座能明显降低桥梁的地震需求，已经逐步成为桥梁抗震设计的首选方案，《铁路桥梁抗震设计规范》中即推荐在也高烈度地震区有条件时采用减隔震设计。减隔震支座的造价、耐久性和可靠性是控制其推广应用的关键。其中，摩擦摆式支座的主要材料是钢材、聚四氟乙烯板，支座的耐久性、稳定性好，是简支铁路桥上使用最为广泛的减隔振支座之一，如图6所示。

1.下座板；2.滑动曲面；3.抗滑螺栓；4.限位滑块；5.滑动块；6.上座板。图6 摩擦摆式支座构造Fig.6 Friction pendulum bearing structure

摩擦摆式支座的基本原理是用滑块沿下支座板的弧面滑动达到隔震目的，沿圆弧面的滑动运动与单摆运动相同，其自振周期完全由弧面半径控制，同时弧面提供了震后的自复位能力。滑块和不锈钢弧面之间的摩擦力还提供了一定的能量消耗能力。

在OpenSEES中，采用Single Friction Pendulum Bearing单元模拟摩擦摆支座。摩擦因数为常数(不随压力、滑动速度和温度变化)，滑动前初始刚度为常数，滑动面为圆弧面。其具体设计参数如表2所示，该摩擦摆式支座的滞回曲线，如图7所示。

表2 摩擦摆支座参数Tab.2 Friction pendulum bearings parameters

图7 摩擦摆支座滞回曲线Fig.7 Hysteresis curve of friction pendulum bearing

抗滑螺栓在剪断前模拟为线弹性元件，剪断后抗力为零。设计剪断力为508.24 kN，剪断位移为2 mm。

一般支座采用Two Node Link 单元模拟，其参数如表3所示。

表3 一般支座参数Tab.3 General bearings parameters

1.4 桥墩和主梁模型

轨道不平顺激励下的车致桥梁振动一般处于线性范围内，因此车-桥耦合振动分析中桥梁一般为线性模型。但采用了减隔震支座的桥梁，地震作用下支座会表现出非线性行为。地震下支座的非线性行为会影响桥面振动的幅值和频率，进而影响到桥上车辆响应。以铁路常见的简支梁桥为例，探讨支座非线性对脱轨危险性的影响。桥梁上部结构为32 m箱梁(双线铁路)，材料为C55混凝土；桥墩高度为20 m，材料为C35混凝土，桥上铺设无砟轨道。不考虑桩土作用，墩底固结。上部结构与桥墩截面特性如表4所示，参照GB 50111—2006《铁路工程抗震设计规范》[14]设计反应谱中阻尼取值，本文桥梁阻尼比选用0.05。

表4 上部结构与桥墩截面参数Tab.4 Superstructure and pier section parameters

桥梁模型包含50跨简支梁：一是为模拟平原地区常见的铁路长桥；二是为了使得地震整个过程中列车在桥上。墩梁之间全部为摩擦摆式支座连接，每跨梁设置4个支座。为说明摩擦摆式支座的效果，另分析了墩梁之间为一般弹性支座的情形。为便于对比2个模型中的桥墩都按线弹性计。

图8和图9给出了设置一般支座的桥梁横向、垂向的基频和振型，图10～图13给出了设置摩擦摆式支座的桥梁振型和频率。其中：图10和图11的支座刚度取滑动前刚度；图12和图13支座刚度取值为滑动启动后刚度。滑动摩擦摆支座滑动启动后，桥梁的一阶横向振动频率从2.402 Hz 降低到1.838 Hz。

图8 设置一般支座桥梁横向基本振型,f=2.581 HzFig.8 Lateral basic mode shape of general support bridge, f=2.581 Hz

图9 设置一般支座桥梁竖向基本振型，f=4.446 HzFig.9 Vertical basic mode shape of general support bridge, f=4.446 Hz

图10 设置摩擦摆式支座桥梁横向基本振型，f=2.402 Hz(滑动前)Fig.10 Lateral basic vibration mode of friction pendulum bearing bridge, f=2.402 Hz (before sliding)

图11 设置摩擦摆式支座桥梁竖向基本振型，f=4.452 Hz(滑动前)Fig.11 Vertical basic mode shape of friction pendulum bearing bridge, f=4.452 Hz (before sliding)

图12 设置摩擦摆式支座桥梁横向基本振型，f=1.838 Hz(滑动后)Fig.12 Lateral basic vibration mode of friction pendulum bearing bridge, f=1.838 Hz (after sliding)

图13 设置摩擦摆式支座桥梁竖向基本振型，f=4.466 Hz(滑动后)Fig.13 Vertical basic mode shape of friction pendulum bearing bridge, f=4.466 Hz (after sliding)

1.5 轨道和桥梁的相互作用力

在C++车辆-轨道程序和OpenSEES桥梁的混合模型中，轨道作用力需要施加到OpenSEES中的桥梁模型中。从图7可知，当第i轨道单元在时间t处位于桥面的节点处时，轨道作用在梁体上的横向，垂直和扭转载荷Hbr,i，Vbr,i和Tbr,i为

(11a)

(11b)

(11c)

式中， 轨-桥作用力和位移变量的含义见图5与1.2节。当轮轨接触点位于2个节点之间时，可以基于形函数的插值确定接触点处的位移。

1.6 轮轨相互作用与脱轨判别

地震作用下轮-轨之间出现剧烈的冲击作用，必须采用容许轮轨脱离和冲击的非线性轮轨相互作用模型。本文的轮轨法向接触关系采用赫兹接触理论，赫兹接触力由轮轨法向压缩量计算。轮轨切向接触采用Shen-Hedrick理论。计算轮轨接触力时的接触几何采用迹线法搜索[15]。

目前通常采用脱轨系数和轮重减载率数作为脱轨判据，这2个指标对脱轨判据的安全冗余很大，作为运营条件下的判据是合适的。但地震是偶然作用，用脱轨系数和轮重减载判别轮对是否掉道是非常保守的，用基于轮轨位移的脱轨判别更为直接[16]。

基于上述非线性轮轨关系，可采用位移脱轨标准，即垂直脱轨和侧向脱轨标准。当车轮的最低点到达轨道的最高点时(车轮提升hmax，如图14所示)，发生垂直脱轨。在这种情况下，横向上的小扰动可能使车轮落在轨道的范围之外。我国的LM踏面与60 kg钢轨对应的为28 mm。

图14 基于车轮位移的脱轨标准(mm)Fig.14 Wheel displacement based derailment criterion(mm)

2 OpenSEES与C++混合模拟及数值算法

地震下的车-轨-桥非线性程序包括两部分：C++开发的车辆-轨道分析程序和OpenSEES中的桥梁动力分析。这两部分通过Python的第三方库Cython进行交互，如图15所示。

图15 交互流程Fig.15 Interactive process

在OpenSEES中地震动选用位移输入法。地震动位移输入从加速度输入积分求得，并消除残余速度和位移。

车-轨-桥动力积分采用作者于2008年提出的分区异步长混合积分思路：在车-轨子系统采用小步长的显式积分，在桥梁部分采用大步长隐式积分。由于桥梁可采用大积分步长(取值为小步长的20～50倍)，该算法效率提高20～50倍。以下简要介绍算法步骤。用Zhai[17]显示积分法求解车辆-轨道动力方程,与其他积分方法相比，翟积分法不需要求对矩阵求逆，对轮轨非线性问题无需迭代求解。车辆和轨道的积分格式相同，以与桥梁交互的轨道系统为例，说明显式积分法的实施步骤。显式积分法的格式：

步骤1已知本时间步和前一时间步的位移、速度和加速度，按如下运动学关系，预测下一步的位移和速度

(12a)

(12b)

步骤2按照(n+1)步的位移和速度，由物理关系(弹簧和阻尼)，计算各部件所受的力,已知各自由度受力后，按下式的动力学关系，算出各自由度在(n+1)步的加速度

(13)

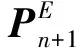
桥梁结构采用隐式积分法(OpenSEES内置)，其积分步长ΔT=mΔt(m=20～50)，即桥梁的分步长ΔT是车-轨步长Δt的几十倍。在一个桥梁积分步长内，车-轨系统积分m次，因此需要解决2个系统间响应的时间衔接问题。图16给出了混合积分法的流程，图中：qr为轨道位移；Yv为车辆位移；Xb为桥梁位移；第2个下标表示积分步序号。

图16 混合积分算法Fig.16 Integrated explicit-implicit algorithm

3 地震下车-轨-桥程序检验

目前无通用的车-轨-桥地震分析软件，为考察本文车-轨-桥模型和程序分析结果的可靠性，采用分环节检验的方法。即通过与商业用多体动力学软件Simpack对比，检验模型中的车-轨地震环节；与车-桥耦合振动程序TTBSIM[19]对比，检验车-轨-桥相互作用。

3.1 地面横向运动下车辆-轨道响应对比

为了对大幅地面运动下的车-轨相互作用环节进行验证，将程序中的桥梁部分移除，直接把地面运动施加在轨道底部的地面上。地面运动位移激励是5个周期的正弦波，在开始和结束处作平滑处理，以减少由于激励加速度不连续性引起的动态系统中的冲击(见图17)。地面运动的幅值使得轮轨出现脱离和碰撞现象。Simpack软件建立的模型，如图18所示，由于Simpack本身不具有地震分析功能，不便直接施加地面位移，改为在车体的各刚体上施加横向惯性力时程来模拟地震作用。从结构动力学基本理论可知，若连接地面的单元是线性的，则加速度输入和位移输入方程是等价的。本文中，线性的轨道元件与地面连接，因此地震动加速度和位移输入等价。

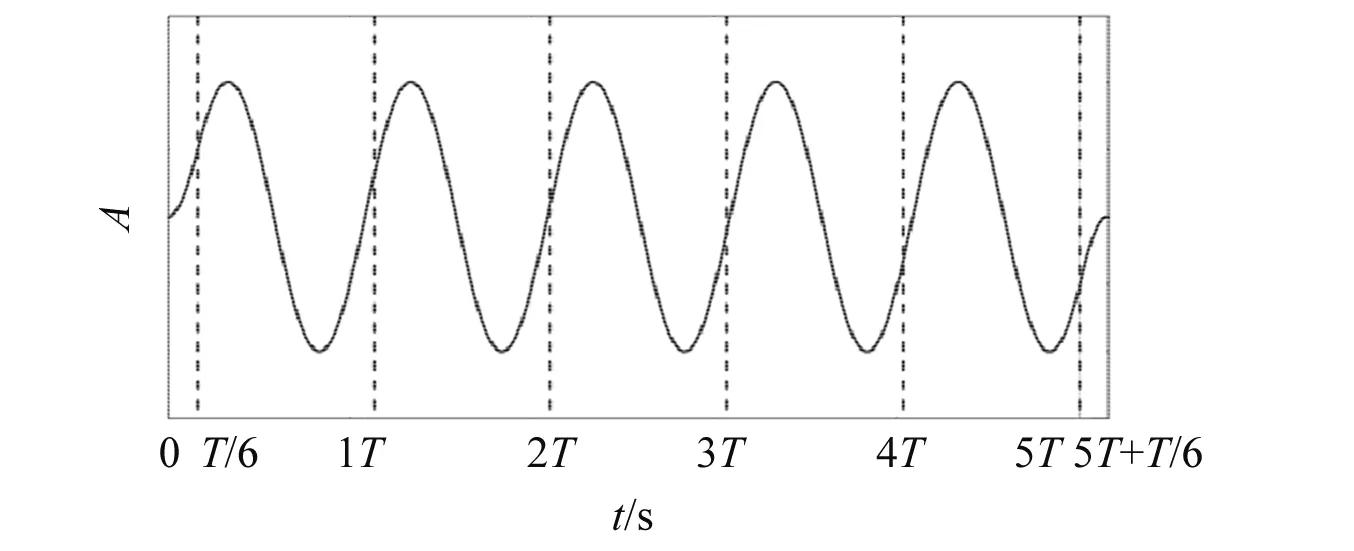
图17 正弦激励Fig.17 Sinusoidal excitation

图18 Simpack车辆-轨道模型Fig.18 Simpack vehicle-track model

共分析了地面运动频率为0.5 Hz与0.8 Hz 2个工况。Simpack程序和本文程序得出的轮轨力对比见图19和图20。可以看出，在轮轨冲击方面:本论文程序与Simpack程序计算出的结果吻合，本程序的车-轨分析结果是可靠的。

图19 轮轨冲击对比f=0.5 Hz， A=310 mmFig.19 Wheel-rail impact comparison f=0.5 Hz, A=310 mm

图20 轮轨冲击对比f=0.8 Hz, A=105 mmFig.20 Wheel-rail impact comparison f=0.8 Hz, A=105 mm

3.2 车-轨-桥相互作用对比

使用车-线-桥动力学仿真通用软件TTBSIM与本论文程序进行对比，本程序的车-轨-桥相互作用进行演示。两程序对单节列车通过简支梁进行模拟，无地震动输入。图21是2个程序给出的桥梁跨中挠度时程曲线，本程序与TTBSIM程序计算出的桥梁跨中挠度的幅值与曲线的形状相同，程序能够反映车-桥相互作用。

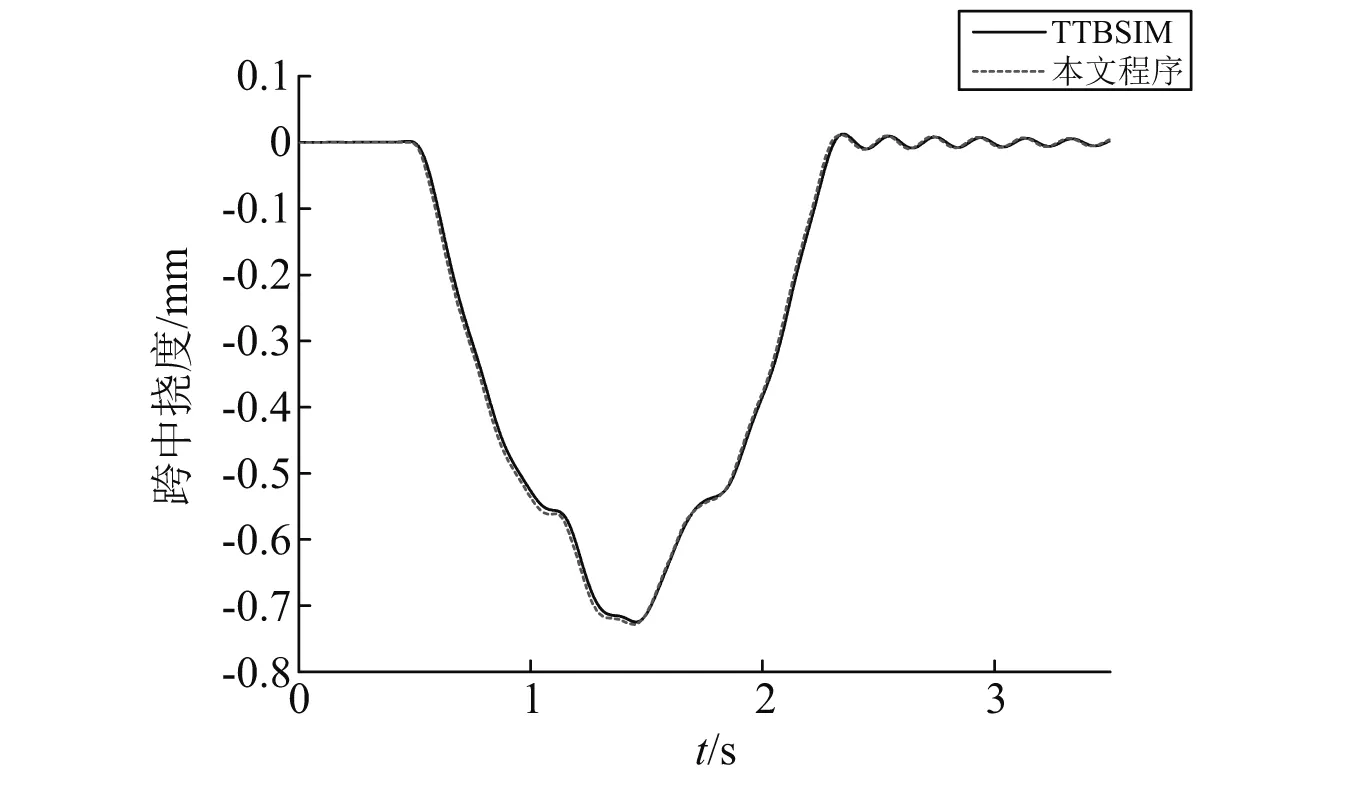
图21 桥梁跨中竖向挠度Fig.21 Vertical displacement of bridge

4 摩擦摆式支座对车-桥响应的影响

车-轨-桥的地震输入选取实测地震动记录，本文采用8条硬岩场地的远场实测地震波。地震动来源如表5所示，加速度反应谱如图22所示(PGA=0.15g)。地震动采用OpenSEES位移输入，车速设定为150 km/h。

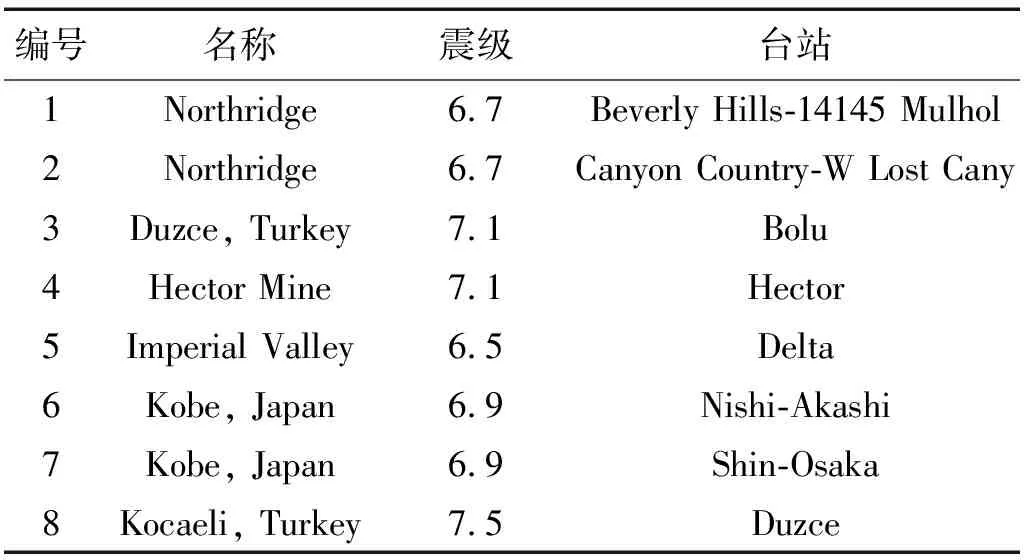
表5 地震动来源Tab.5 Ground motion source

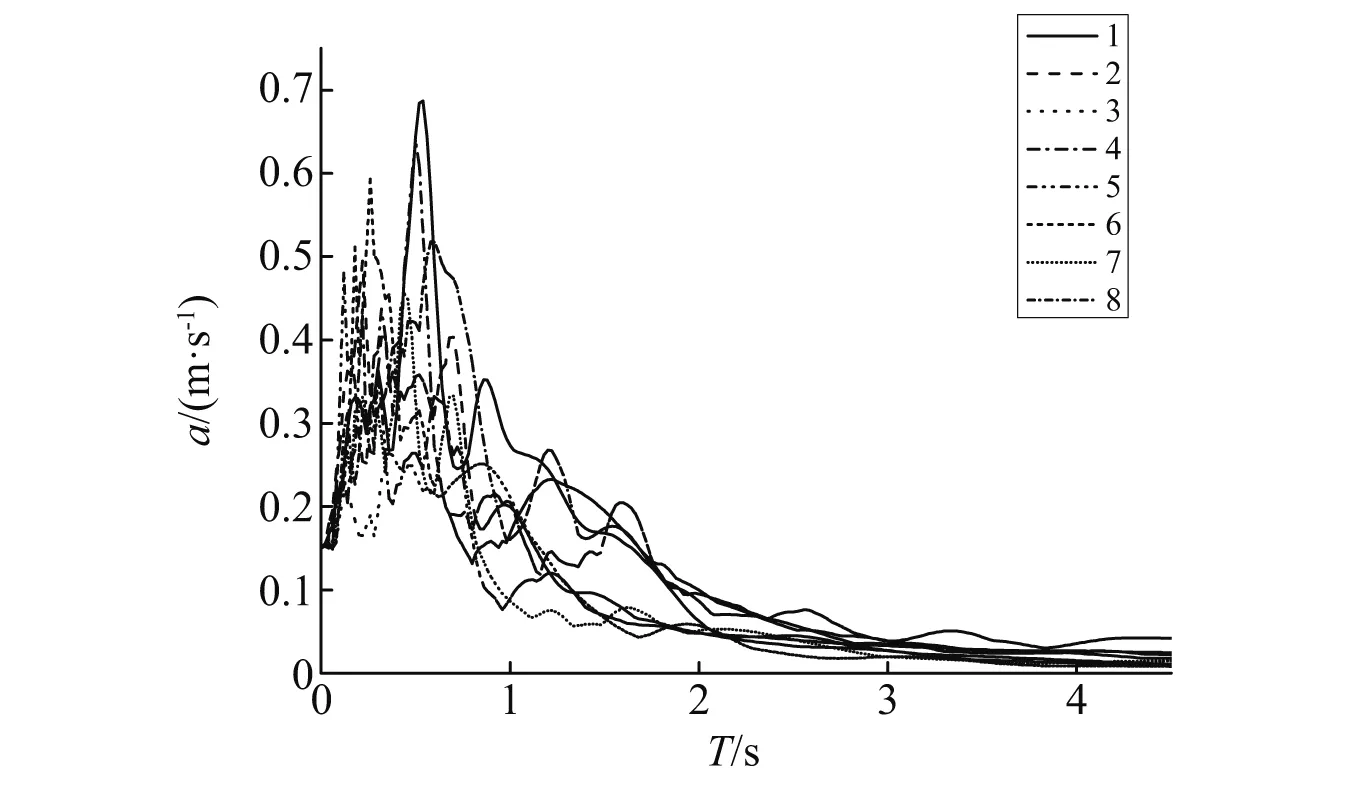
图22 地震反应谱Fig.22 Seismic response spectrum

4.1 对桥梁响应的影响

在表5中第1条地震波(PGA=0.15g)作用下，设置普通支座和摩擦摆支座桥梁的车-轨-桥响应对比见图 23～图26。可以看出，摩擦摆支座的限位销钉在6 s左右被剪断，支座上下摆出现滑移。设置一般支座模型的桥面峰值位移、加速度、墩底横向剪力与弯矩分别为10 mm， 2.9 m/s2，4 700 kN和96 000 kN·m。设置摩擦支座的桥面峰值位移、加速度、墩底横向剪力与弯矩分别为59 mm，1.4 m/s2， 2 000 kN和45 000 kN·m。可见设置摩擦摆支座后，桥梁的横向位移放大了6倍，而且还出现了残余位移；但桥梁加速度、墩底剪力和弯矩分别降低了51%，57%和53%。

图23 桥梁横向相对位移Fig.23 Bridge lateral relative displacement

图24 桥梁横向绝对加速度Fig.24 Lateral absolute acceleration of bridge

图25 墩底横向剪力Fig.25 Lateral share force at the bottom of the pier

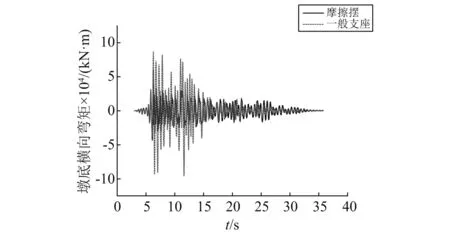
图26 墩底横向弯矩Fig.26 Lateral bending moment at the bottom of the pier

在表5中的8条地震波作用下，做动力增量分析，探讨摩擦摆支座的影响随地震动PGA的变化。图27～图30给出了1～8号地震动下桥面横向最大相对位移、横向最大绝对加速度、墩底横向最大剪力与最大弯矩随PGA变化的关系，虚线表示一般支座，实线表示摩擦摆支座。可以看出：在PGA>0.15g后，设置摩擦摆模型的响应与一般支座模型响应开始出现显著的差别。摩擦摆相比于一般支座，桥面横向相对位移增大，绝对加速度，墩底剪力与墩底弯矩减小。随着PGA的增大，差异愈发明显。

图27 桥面横向最大相对位移Fig.27 Maximum lateral displacement of bridge

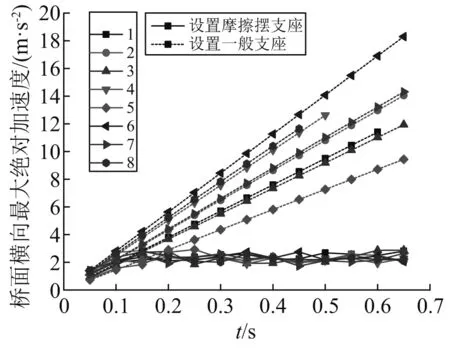
图28 桥面横向最大绝对加速度Fig.28 Maximum lateral absolute acceleration of bridge

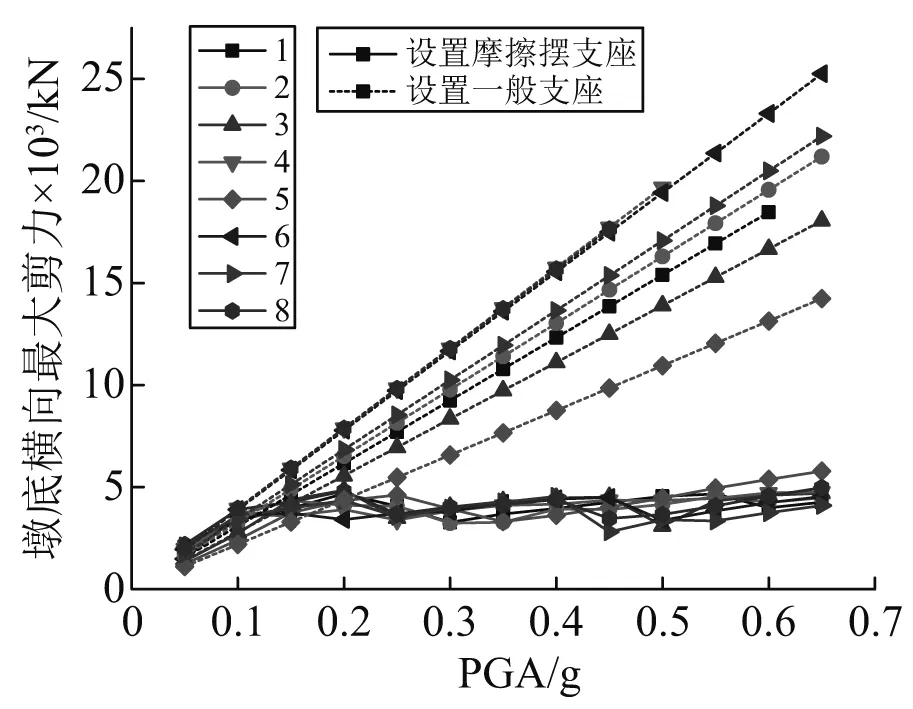
图29 墩底横向最大剪力Fig.29 Maximum lateral shear force at the bottom of the pier

图30 墩底横向最大弯矩Fig.30 Maximum lateral bending moment at the bottom of the pier

4.2 对车体振动的影响

图31和图32给出了1号地震动(PGA=0.15g)下的车辆绝对加速度与绝对侧滚加速度时程。可以看出：设置摩擦摆支座的桥上车辆横向加速度和侧滚加速度峰值明显小于一般支座的桥上车辆。图33和图34给出了车体横向绝对加速度与侧滚加速度的峰值随PGA的变化(实线为设置摩擦摆支座的模型)，在PGA>0.15g后，相同地震动输入下，设置一般支座的桥上车辆横向绝对加速度与侧滚加速度大于设置摩擦摆支座的桥上车辆。

图31 车辆横向绝对加速度Fig.31 Vehicle lateral absolute acceleration

图32 车辆绝对侧滚加速度Fig.32 Vehicle absolute rolling acceleration

图33 车辆横向最大绝对加速度Fig.33 Vehicle maximum lateral absolute acceleration

图34 车辆最大绝对侧滚加速度Fig.34 Vehicle maximum absolute rolling acceleration

4.3 对轮轨相互作用的影响

图35～图38给出了1号地震动下(PGA=0.15g)轮轨相对横移、垂向位移、脱轨系数与减载率时程，可以看出摩擦摆模型的上述各项响应的最大值都小于一般支座模型。

图35 轮轨相对横移Fig.35 Wheel-rail lateral displacement

图36 轮轨抬升量Fig.36 Wheel lifts

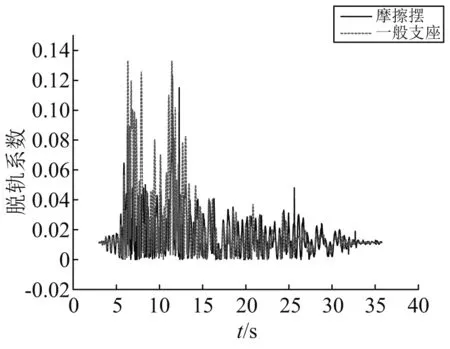
图37 脱轨系数Fig.37 Derailment factor

图38 减载率Fig.38 Wheel load reduction rate

图39～图44给出了上述响应的最大值随PGA的变化，在PGA较小时，摩擦摆模型上述响应的最大值与一般支座模型差别不大。随着PGA增大，设置一般支座模型的轮轨相互作用响应迅速增大；而设置摩擦摆支座的桥梁，轮轨响应随PGA的增大相对平缓。

图39 轮轨最大相对横移Fig.39 Maximum wheel-rail lateral displacement

图40 轮轨最大抬升量Fig.40 Maximum wheel lifts

图41 轮轨最大横向力Fig.41 Maximum wheel-rail lateral force

图42 轮轨最大垂向力Fig.42 Maximum wheel-rail vertical force

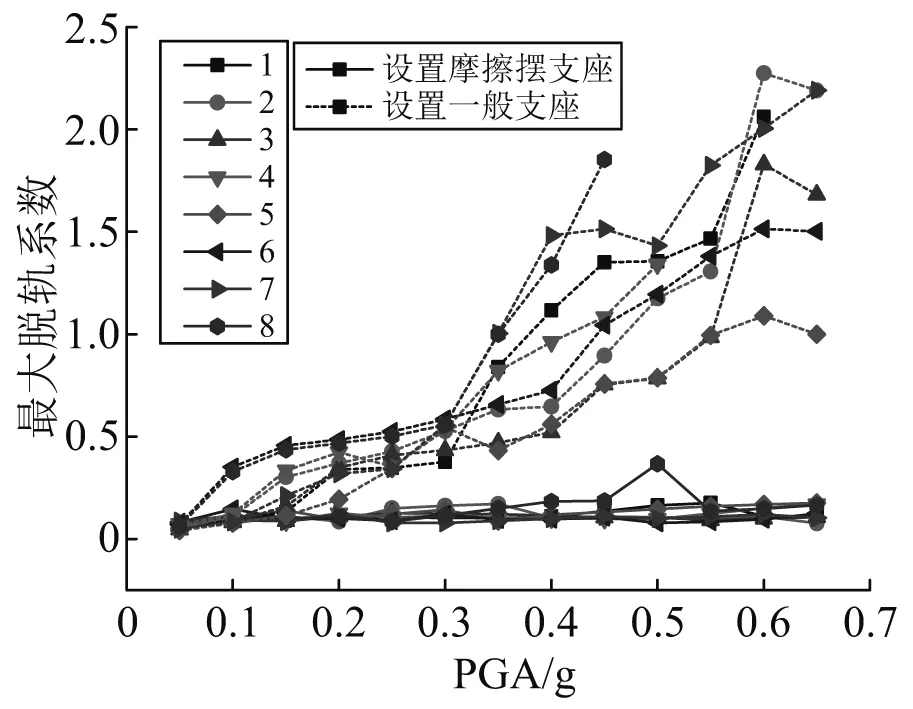
图43 最大脱轨系数Fig.43 Maximum derailment factor

图44 最大减载率Fig.44 Maximum wheel load reduction rate

5 结 论

本文采用31自由度的车辆模型、移动断面模型、高度非线性的轮轨接触模型建立非线性的车-轨分析模型，运用OpenSEES建立桥梁有限元模型，并通过分区异步长积分算法求解车-轨-桥响应。研究了摩擦摆支座对高速铁路行车安全性的影响。

研究表明，在横向地震动作用下，桥梁采用摩擦摆支座会加大桥面横向位移，并产生残余位移。在大震作用下，摩擦摆支座能够大幅度降低车体的横向与侧滚加速度，降低轮轨相对横移、抬升量、横向和竖向轮轨力、脱轨系数与减载率，可见对于本文研究的简支梁桥，设置摩擦摆支座后，地震作用下车辆脱轨指标(轮轨力、轮轨位移)有所降低。