城市排水管道清理机器人变径机构优化设计

肖 程，涂福泉，幸 垚，雷 达

（1.武汉科技大学 冶金装备及其控制省部共建教育部重点实验室，武汉 430081；2.三峡大学 国际文化与交流学院，宜昌 443000）

0 引言

随着我国城市化建设如火如荼的进行，老旧的地下管网已不能满足城市居民的日常生活排水需求，城市排水管道担负着集运送城市污水、雨水的重要功能[1]。在每年的汛期，大部分老旧城区会遇到排水道堵塞而导致的“水漫金山”式的内涝，而排水管道日常难以清理造成淤泥的堆积、积垢正是重要的影响因素之一。影响排水管道堵塞主要有两个方面的因素[2]：一是由于排水管道的更新建设没能跟上城市化建设的步伐，当污水流量突增时来不及排出导致堆积；二是由于排水管道管理运营的不合理，管道由于没能定期的科学维护出现结垢、腐蚀等问题影响了管道的输送能力。排水管道中沉积物的累积不仅会减小排水管道的输送空间,且会增大水流阻力,从而影响管道的过流能力,当沉积物累积达到一定程度时甚至会造成堵塞,影响整个排水系统的正常运行。管道沉积物包含的固体颗粒物质为细砂和来自雨水和污水的悬浮固体[3]。城市排水管道一般浸泡在污水中，而污水中还有大量的腐蚀介质，腐蚀介质生成物破坏了水泥的胶凝结，长期作用会进一步侵蚀水泥造成管道的凹陷[4]。因此需要一种能有效为城市管道清理、检测的手段来适应城市发展需求。

近年来，国内外学者和工程技术团队在管道机器人的发展上取得了很大的进步。Choi等人通过采用被动自适应机制和多电机独立驱动方法开发了MRINSPECT系列管道机器人，可以通过独立控制电动机的速度来实现机器人的速度和差速运动[5]。王佳等人把球形机器人和管道爬行机器人相结合采用两个伺服电机作为动力输入，设计出了一种可以全方位的运动的球形管道机器人[6]。李鹏等人设计了螺旋驱动的管道机器人，采用单电机作为动力源来驱动调节机构进行约束，同时构建了摄像机的搭载平台，方便了机器人稳定检测周围复杂的管道环境[7,8]。张学文等人提出了一种由三轴差速机构和管径适应机构组成的管道机器人，该机器人的驱动部分由驱动电机来驱动三轴差速机构，并由三轴差速机构并联驱动沿周向均布的3个锥齿轮副，锥齿轮又通过同步带来带动驱动单元的前行走运动，前行走轮组经同步带把运动传递到后驱动轮组，从而实现驱动单元由一个电机驱动、三路差动输出的目标[9,10]。许冯平等人针对油田生产特殊工艺井测井的特殊要求提出一种基于并联机构的蠕动式行走管道机器人来解决在细长管道空间适应性问题[11]。张延恒等人提出了一种采用双球头结构、具有柔性软轴及电磁吸合装置并能实现自发电的管道仿生柔性蠕动机器人[12]。

管道机器人按照运动方式的不同主要可以分为蠕动式、履带式、脚式、轮式等种类，不同的运动方式又各有其自身的缺点，如越障能力不强，转弯性能较差，适应管道的尺寸过于单一，软硬件控制技术困难等[13]。因此，针对城市管道长时间的污水腐蚀造成的管道内凹坑、污垢堆积而成的凸起等缺陷以及管径变化造成的台阶和沟槽等恶劣环境条件，提出了一种对管径具有更好的适应能力的履带式清理机器人。

1 机器人整体结构

提出的变径机构组块是由沿机器人轴向间隔120°均布的三组并联支撑杆系组成，根据管道环境的特殊性，管道机器人要求保证φ500mm～600mm变径范围及牵引装置最低600N牵引力，机器人的结构设计如图1所示。采用三轴对称结构提高了机器人管运动的稳定性，步进电机驱动丝杠螺母旋转从而控制机器人的平行四杆联动机构，实现了机器人结构的同时缩放，通过减速电机来控制清理杆组的运动达到对排水管道污垢清理的目的。当机器人在管道中行走时，通过直接控制步进电机来改变机器人的径向尺寸，从而使机器人在设计范围内对管径具有良好的适应性。

图1 机器人三维简图

机器人在变径过程中会导致机器人重心与管道的中心线发生偏离从而使运动不稳定，因此可以在径向调节机构上加装一个压力补偿装置，以确保机器人在复杂环境运行中都能稳定运动。针对机器人补偿管壁压力的问题设计了弹簧调节机构。该设计考虑了牵引力的调整和管径的主动适应，具有一定的柔韧性和调节空间。当机器人的三个轴完全接触到管壁上时，步进电机将继续驱动螺母使弹簧进一步压缩，从而通过弹簧将附加驱动力提供给管壁实现管壁压力补偿。与全刚性结构设计相比，机器人具有一定的调节余度空间，当遇到小的障碍物时，机器人可以以被动压缩弹簧的形式完成运动，从而增强了机器人的环境适应性。丝杠螺母上面的压力传感器通过检测弹簧的压力间接测出管道对机器人的压力值，检测到的压力信号作为反馈信号通过调整所设计的柔性机构实现对机器人运动的精确控制。

2 自适应机构受力分析

变径机构如图2所示采用曲柄滑块机构，中心盘移动使曲柄转动推动履带足升高或降低达到变径目的。当行走机构受到管道空间的约束，径向发生微小变化时，在主动径向调节来不及响应时，连杆系统可以带动推杆来压缩中心盘上面的弹簧，来抵消管径变化，使行走机构在径向具有一定的柔性。

取变径机构的一组作为分析对象，机器人牵引力FR和法向压力FN的关系为：

式中：μ为车轮与管道内壁的附着系数。

图2 自适应机构简图

将车轮认为是质量分布均匀的理想状态，根据几何关系可得出：

式中：R1是支撑杆AB的长度，R2是支撑杆上C、E之间的距离，R3为顶杆EF的长度R4是连杆BD的长度，α、β分别为杆CD、EF与水平方向的夹角。

对式(2)进行微分：

忽略车轮自身重力的影响，由虚功原理得：

由式(3)、式(4)可以得到管道对机器人的变径瞬时压力与水平推力的关系：

三组车轮对中心盘的总推力为：

在变径时，水平总推力与电机转矩的关系可由式表示为：

式中，η为滚珠丝杠螺母副传递效率；T为电机输入转矩；ph为丝杠导程。

3 变径机构优化设计

3.1 设计变量

由上述分析可知，R1、R2、R3、α 和β等参数确定了管道机器人变径机构，而α与β会随着变径机构的运动而不断变化且β能用α的关系式表达综合考虑到机器人的径向尺寸与丝杠的导程问题可以取α=35°的初始值进行仿真计算，因此设计变量取为：

3.2 目标函数

变径机构的性能特性可以用电机的转矩T的大小作为评判标准，而由式(7)可知水平推力Fε与电机转矩成正比，则可以最大水平推力为优化的目标函数。

3.3 约束条件

根据几何关系和管道变径的范围要求可得到约束条件：

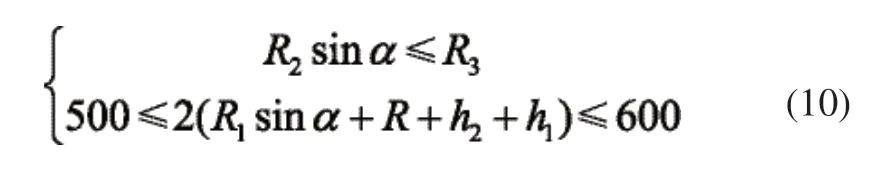
其中R是车轮半径。

3.4 参数化建模与优化设计

参数化设计是将确定的机构尺寸用变量进行代替，通过对模型进行设计研究、试验设计和优化计算并对优化结果进行分析，得到满足目标函数的最优变量。由上建立的力学模型可知各个变量与目标函数之间的关系，在ADAMS中创建相关的变量及关键点。

表1 设计变量/常量

根据变径机构结构简图所示，使用几何建模工具连接各个关键点生成运动件，通过约束工具创建各构件之间的基本约束，为了简化模型，将中心盘与轴套的滑动简化为滑块与地面的滑动。在滑块与大地之间添加压缩弹簧，弹性系数K=100N/mm，阻尼系数C=1N·s/mm，在连杆中心处施加方向垂直向下大小为333N的力，等效于管道对车轮施加的封闭力FN，建立的变径机构简化模型如图所示。

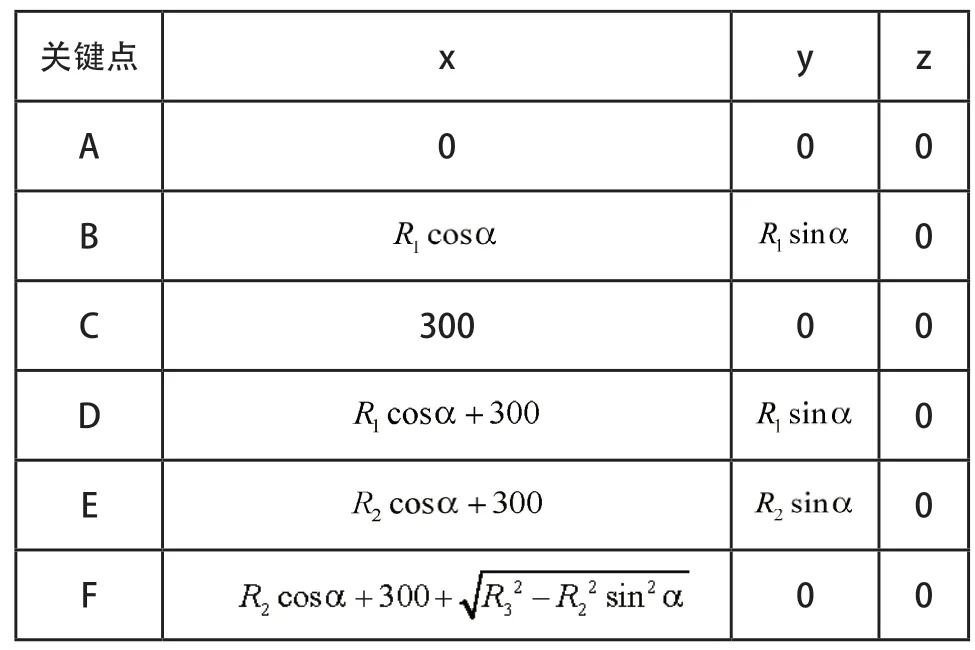
表2 关键点参数坐标

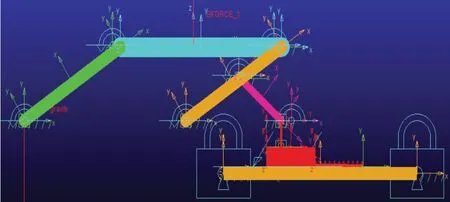
图3 ADAMS优化模型

完成建模之后，可以建立测量作为目标函数来进行优化计算。在自适应变径机构模型中，为了获得运动过程推力的大小，以弹簧的柔性力变化作为测量指标，将柔性力的最大值作为评判标准，将各优化曲线中柔性力的最大值的最小值作为优化目标，得到柔性力参数优化结果如图4所示。

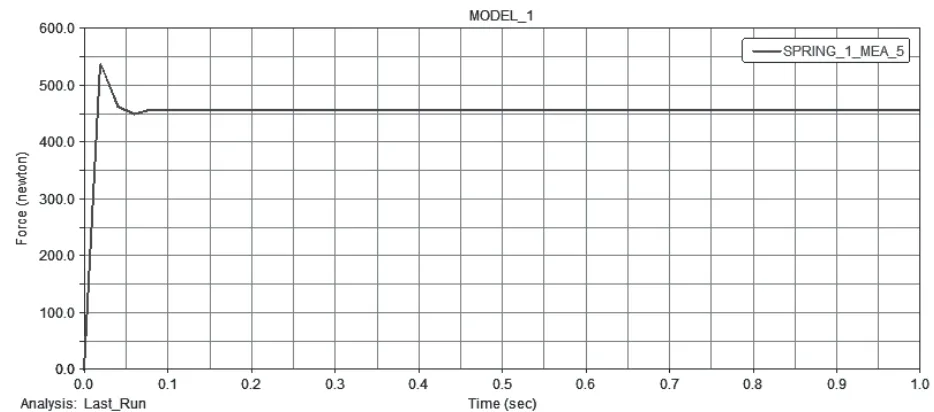
图4 弹簧柔性力初值仿真图

从图4中可以看出在用初始值进行仿真计算后，柔性力在0.02秒内迅速增加并在0.02秒处取得最大值537N，在0.02秒～0.06秒内又逐渐减小最后柔性力稳定在456N。经过迭代设计试验后，从图5柔性力优化曲线可以看出，在Trial3模式下，弹簧柔性力的峰值Fεmax最小为523N。

图5 柔性力稳定曲线

根据各变量的取值范围，以机构变径运动中弹簧柔性力峰值最小为目标函数，通过ADAMS内置算法OPTDES-GRG进行优化设计，柔性力的最大值优化曲线如图6所示，优化结果如表3所示。

表3 参数优化前、后对比

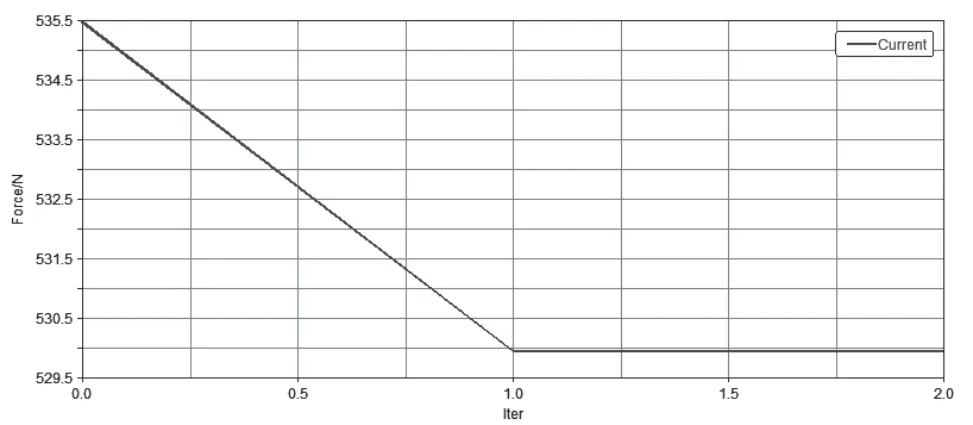
图6 优化设计图

4 结语

提出的柔性调节排水管道清理机器人与传统刚性调节管道机器人相比有更好的管径调节性能，能有效防止电机因为过载而发生的损坏。本文分析了调节机构的力学性能并利用ADAMS以弹簧柔性力最大值最小化为目标进行了优化实验，得到了约束条件下的最优杆长，提高了管道机器人的变径性能。