基于LTSA的芯片固化温度场时空建模方法

刘 硕，张师源，林 朗

（中南大学 机电工程学院，长沙 410083）

0 引言

芯片固化环节是半导体芯片生产的一个关键过程，该环节需要在固化炉内进行。在固化过程中，环氧树脂等材料通常需要特定的固化温度，以及稳定均匀的温度场分布[1]。因此，对固化炉温度场的分析与控制有很高的要求，而分析与控制的关键，就是对炉内温度场建立一个准确、可靠的模型。

固化炉的热动态过程属于典型的非线性分布参数系统（Distributed Parameter System，DPS），通常用偏微分方程（Partial Differential Equation，PDE）来表示[2]。DPS具有无限维时空动态特性以及非线性特性，因此精确的PDE很难获得。在工程应用中，通常将无限维DPS近似为有限维的常微分方程（Ordinary Differential Equation，ODE）[3]，所以模型的降阶技术是非常重要的。

对于模型已知的DPS，邓华[4]等提出了一种基于谱近似的智能建模方法，将谱方法用于时空分离和模型降维，得到低阶ODE模型，并设计了神经网络观测器用于ODE的状态估计；蒋勉[5]将谱方法所得到的基函数进行展开和截断获得系统的最优基函数，并通过传统智能方法来近似系统时间动态，得到了热轧过程的时空耦合模型。但是由于在工程中很难确定系统结构和参数，所以上述方法不便于对实际工业过程应用。

对于模型未知的DPS，基于数据的Karhunen-Loève（KL）方法已经被广泛使用。NejibSmaoui[6]对两个偏微分方程的仿真数据进行KL分解，得到其数据系数，利用神经网络模型预测数据系数，得到了一个智能神经网络模型；Qi C等结合KL与传统的集中参数方法，提出了KL-Hammerstein模型[7]、KL-Wiener模型[8]、KL-Volterra模型[9]；Liu Z[10]等提出了一种适用于锂离子电池温度分布在线估计的KL-极限学习机（Extreme LearningMachines，ELM）模型，使用ELM对时间系数进行拟合。传统的时空分离建模中，KL方法是一种线性降维方法，其得到的空间基函数不能完全精确的表达系统的非线性特征。

本文提出一种基于局部切空间排列（Local Tangent Space Alignment，LTSA）[11]的炉温时空建模方法，该方法是一种基于数据的非线性建模方法，利用LTSA对芯片固化温度数据进行时空分离和降维，得到的空间基函数可以更精确地表达系统的非线性特征。然后将时空数据投影到空间基函数上，得到低阶的时间系数。利用一种智能学习算法径向基神经网络（Radial Basis Function Neural Network，RBFNN）拟合低阶时间系数，该方法能够处理系统内部的非线性规律，并且可以克服局部最小的问题[13,14]。最后通过时空合成，得到固化温度场的全局时空温度分布。通过在实验室简易固化炉上采集的数据进行建模分析，并与传统的KL时空建模进行比较。结果表明该方法拟合效果比较准确，对于工业热过程的分析与控制具有良好的意义。

1 问题描述

芯片固化炉的热动态过程是一个二维的分布参数系统，其分布在x和y方向上的热过程可以表述为：

其中，T（x，y，t）为时空分布的温度，℃；ρ为炉内传热气体的密度，kg/m3；cρ为传导介质的比热容，J/（kg.℃）；λx和λy为传热介质在x和y方向的传导率，W/（m.℃）；Q（x，y，t）为热源，W/m3；h为对流传热的传导率，W/（m.℃）；Tair为环境大气的温度，℃；x，y为炉室内的坐标，m；t为时间变量，s。

2 基于LTSA的时空建模策略

提出了一种基于LTSA的时空建模策略，通过非线性降维方法局部切空间排列（LTSA）来代替传统的KL方法对模型进行降维，获得空间基函数和低阶时间系数，利用径向基神经网络（RBFNN）对时间系数进行建模，通过时空合成，得到全局的固化炉温度场时空分布。

在基于数据的时空分离框架下，将时空变量T（S，t）写成时空分离的形式，如下：

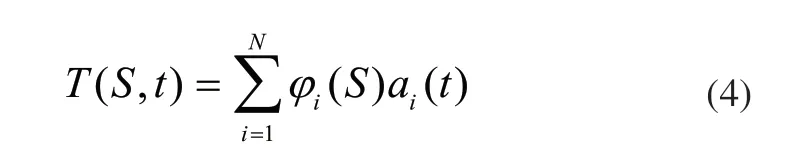
得到空间基函数之后，将时空分布的数据T（S，t）向基函数上投影，即可获得对应的时间系数：

括号表示内积，得到时间系数之后，对其使用基于数据的方法建模，建模预测时间系数为得到后，进行时空重构，获得全局的温度场时空分布：

2.1 局部切空间排列

局部切空间排列算法（LTSA）是一种局部非线性降维方法，在降维过程中可以保留系统的非线性特征。算法主要思想是利用样本点邻域的局部切空间来表征局部的几何性质,然后将局部切空间进行排列得到全局的低维坐标 。算法的主要步骤如下：

1）局部坐标拟合

将Xi中心化，得到为邻域矩阵中心点，对中心化邻域矩阵进行奇异值分解，其前d个最大的奇异值对应的左右奇异向量构成的矩阵为Qi、Vi。所以局部切空间中样本点的局部坐标矩阵为：

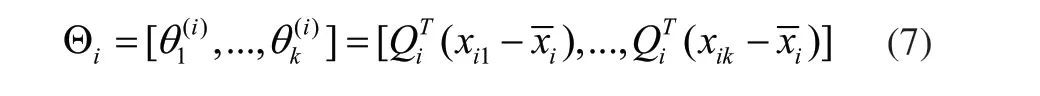
2）局部坐标排列

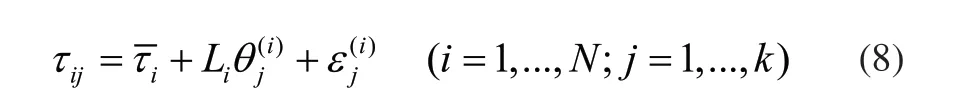
其中，Li为待定的映射矩阵；为重构误差；是τi的中心化矩阵。记则式(8)可以被转化为矩阵形式：

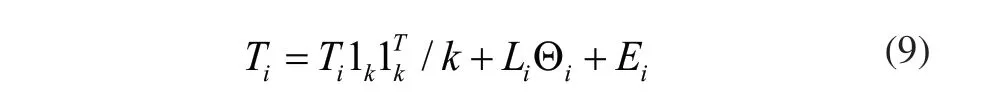
极小化重构误差来保证局部坐标的低维特征：

2.2 径向基神经网络

径向基神经网络（RBFNN）是一种可靠的前馈神经网络，一般具有三层的网络结构，能够处理系统内部难以理解的复杂的函数关系，可以找到系统的最佳逼近，很好的逼近任意非线性函数。RBFNN具有训练速度快、逼近效果好等优点，且不会陷入局部最小的麻烦。RBFNN的基本结构分为三层：输入层、输出层和隐含层，其结构示意图如图1所示。

图1 RBFNN基本结构

其中输入层、隐含层、输出层的节点个数分别为m、n、k，xi表示输入层第i（i=1，…，m）个节点的输入信号，yj表示输出层第j（i=1，…，k）个节点的输出信号，hs（X）为隐含层第s（s=1，…，n）个节点的激活函数，wsj表示连接第s个隐含节点和第j个输出节点的权值。

输入层主要作用为输入信息到系统中，与隐含层之间没有权值连接，不改变数据，输入信号需要进行归一化处理。

隐含层主要作用是通过激活函数对输入信息进行处理，并将处理后的数据传递到输出层，其神经元个数根据实际需要来具体确定。激活函数为径向基函数，通常使用高斯径向基函数。高斯径向基函数是一个非线性函数，可以将系统输入变换到高维进行处理，具有局部响应的特征，其表达式如下，其中，cs和δs为第s个神经元激活函数的中心和宽度：

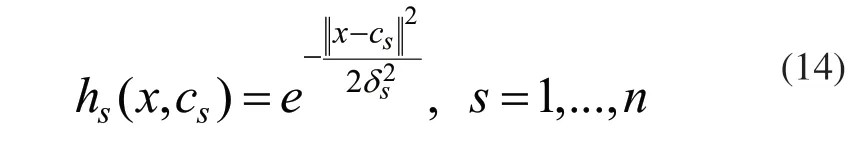
输出层主要作用是通过线性函数对隐含层的输出进行响应。其每个节点和隐含层各个节点有权值连接，通过加权求和得到径向基神经网络的最终输出，如下：

3 实验验证

本文利用实验室自制芯片固化炉进行固化热过程的实验，利用dSPACE实时半实物仿真平台进行加热板控制信号的传送和固化炉温度数据的采集。

3.1 实验系统

芯片固化炉的结构如图2所示，四个相同的700W加热板均匀分布在其内部，每个加热板由一个脉宽调制信号（PWM）控制，引线框架水平面上均匀的布置16个相同的传感器，负责采集温度信息。传感器的平面位置分布如图3所示。

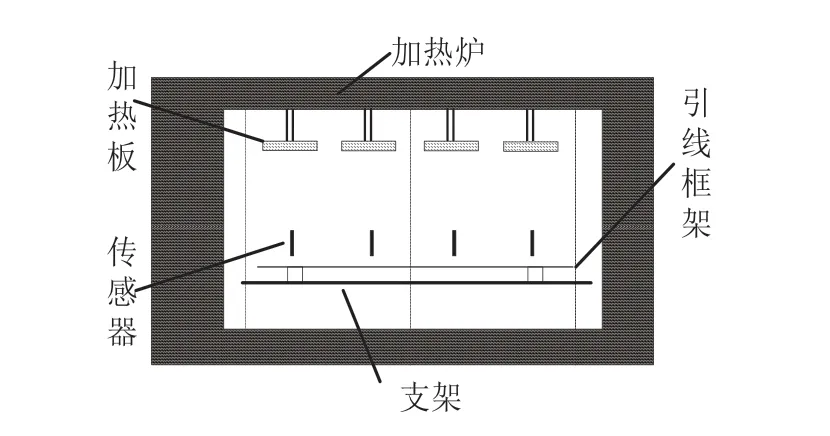
图2 芯片固化炉结构图

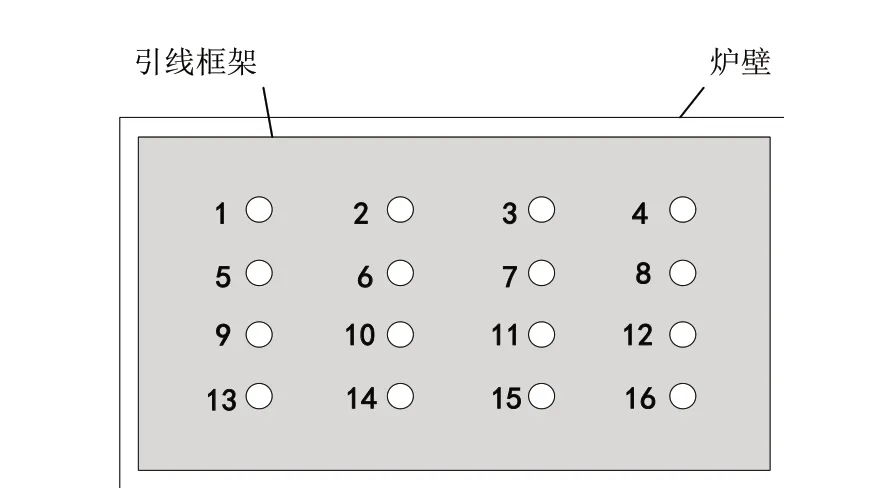
图3 热电偶传感器的平面分布

dSPACE实时系统是由德国dSPACE公司研发的一套基于MATLAB/Simulink的实时控制与测试平台。该系统实现了与MATLAB/Simulink的无缝连接，并可以进行代码的自动生成，无需编程即可实现控制策略的测试与应用，已广泛的应用到机器人、工业控制、无人等领域。

本文所使用的dSPACE实验平台以DS1006板卡为dSPACE系统的处理器，与主控计算机相连并进行数据交换。通过MATLAB/Simulink制定合适的控制策略，并通过DS2103板卡和继电器将控制信号PWM波输出到加热板上。通过热电偶传感器采集固化炉温度信号，经过DS2002板卡传输到dSPACE系统，并输入到控制计算机中。图4为dSPACE实验平台的硬件框图。

图4 dSPACE实验平台硬件框图

3.2 实验结果

实验通过dSPACE系统控制固化炉温度到190℃左右，然后输入随机的PWM占空比信号，其中第三个加热板的输入信号如图5所示。采集2800组实验数据，采样间隔为10s，其中前1400组实验数据用于训练模型，后1400组实验数据用于测试模型的效果和精度。

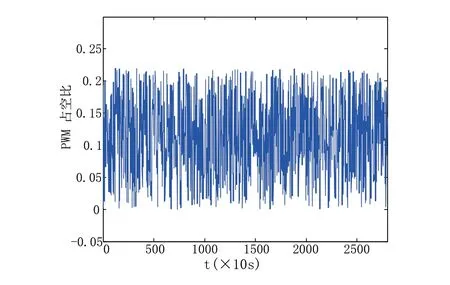
图5 加热板3 PWM输入信号

对训练数据使用LTSA算法进行时空分离和降维，邻域点为13个，空间基函数的阶数为n=5，获得五阶空间基函数。其中，第二阶和第四阶的空间基函数如图6所示。

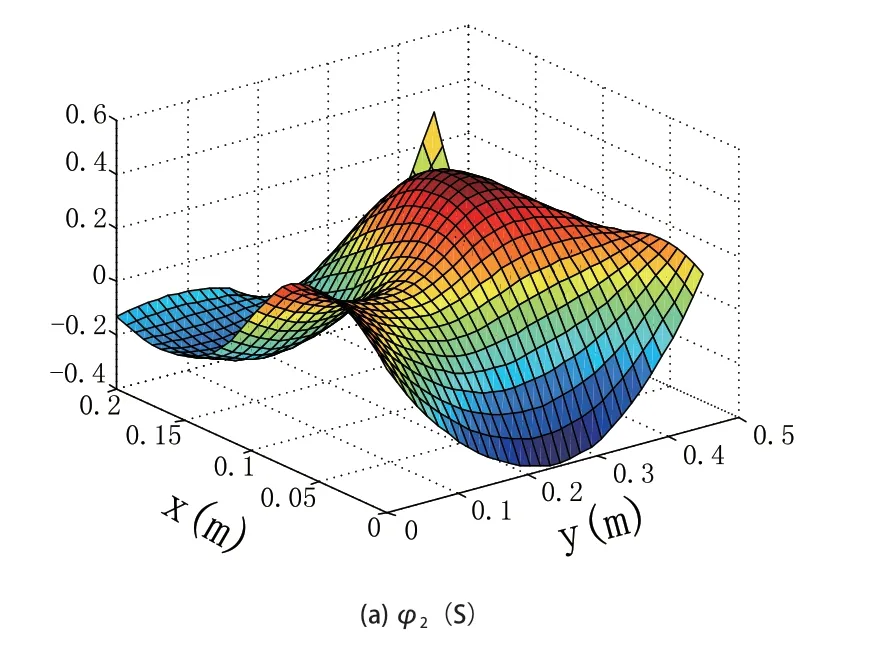
图6 第2阶与第4阶空间基函数

将时空分布的温度数据向基函数上投影得到相应的时间系数ai（t），使用RBFNN模型来近似时序动态特性，输入为四块加热板的PWM输入信号，输出为时间系数，其隐藏层节点个数选为100。使用训练数据训练模型，使用测试数据验证模型的准确性。测试数据的第二阶和第四阶时间系数拟合效果如图7所示，其中蓝色表示模型预测值，红色表示真实值。从图中可以看出，模型具有很好的拟合准确度。

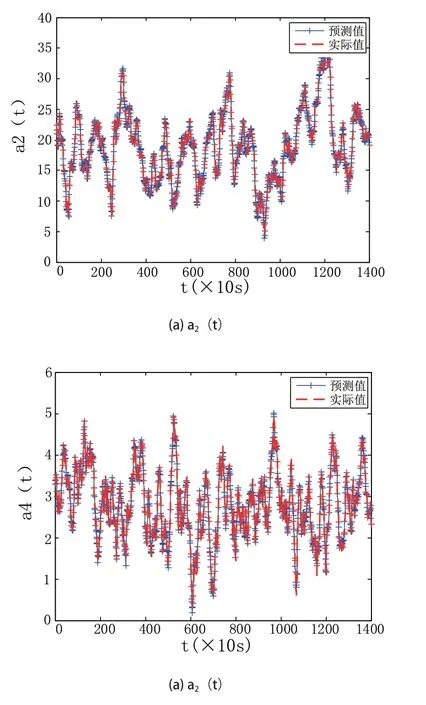
图7 时间系数拟合效果

将空间基函数φ（S）和预测输出的时间系数进行合成，得到时空分布的温度场为了评价所建立模型的精确度，给出以下几个误差指标。

选取11号传感器观察模型在测试数据上的效果，其中图8为预测温度和实际温度对比，图9为11号传感器的相对误差（ARE）。11号传感器的温度数据在测试数据上的最大误差为1.9697℃，最大相对误差为1.09%，相对误差基本在1%以内。因此，模型对于固化炉温度场的预测精度是比较高的。

图8 11号传感器预测数据与实际数据对比

图9 11号传感器相对误差分布

选取最后一个时间点即28000s时，将模型输出的温度数据进行三阶插值，得到此时刻的固化炉温度场全局空间分布。图10为该时刻模型预测温度空间分布，图11为该时刻模型输出的相对误差分布。可以看出模型在空间上的相对误差大约都在1%以内，精度较高，可以准确预测固化炉温度场。

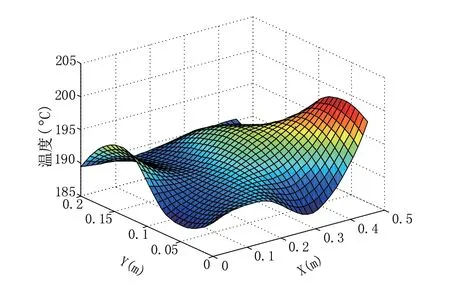
图10 28000s时模型预测温度分布

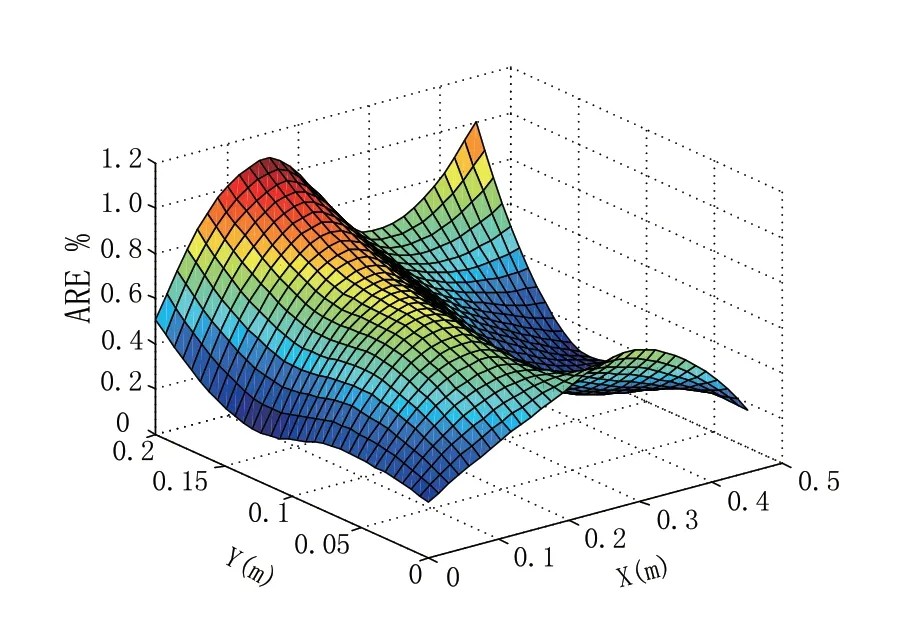
图11 28000s时模型预测相对误差分布

为了展现所提出的模型与KL方法的对比，使用同样的实验环境和实验数据，通过KL-RBFNN对固化炉温度场进行时空分离建模。两种方法误差对比如表1所示，从表中可以看出，所提出的基于LTSA的时空分离策略建模精度比传统的KL要高。

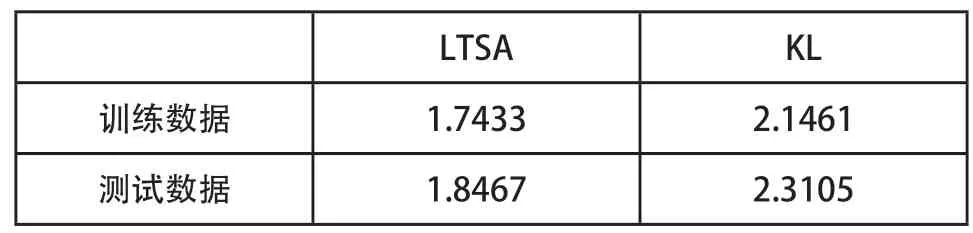
表1 两种方法的RMSE值对比

4 结语

1）提出了一种基于LTSA的时空建模方法，对芯片固化炉炉温系统进行了基于数据的建模分析，实验结果可以看出，该方法对于固化热过程的建模比较有效。

2）与常用的KL-时空模型进行了比较，相较于KL-时空模型，该模型的精度更高，并且适用于实际工业热过程，对工业典型热过程的建模与分析具有良好的价值。