引入橡胶衬套的车辆七自由度振动模型分析

刘 芳，曹娇娇，李 广，檀润华

（1.河北工业大学 机械工程学院，天津 300401；2.国家技术创新方法与实施工具工程技术研究中心，天津 300401；3.中汽研（天津）汽车工程研究院有限公司，天津 300300）

0 引言

车辆平顺性是车辆的重要性能之一。关于车辆平顺性的研究可以分为两个方面：评价研究和改进研究。评价研究包括主观评价和客观评价。改进研究主要包含振动模型的改进、振动模型响应的求解以及零部件研究等。其中整车振动模型的研究是改善车辆平顺性的重要方法。

国内外对车辆振动模型的研究比较早。杨鑫[1]通过建立二自由度1/4车辆悬架振动模型，研究了车辆振动特性对车辆平顺性影响。彭亚琪[2]通过分析对比几种自由度振动数学模型，选取七自由度振动模型为整车优化模型。Sayers[3]建立的18自由度振动模型等具有典型的代表性。已有整车振动研究所建立的振动模型大多基于系统级别，对于部件间橡胶衬套连接件对平顺性影响的研究却较少。

橡胶衬套力学特性包括静态力学特性和动态力学特性。对于橡胶衬套的研究，国内陈茜[4]、邱实[5]等人通过ABAQUS建立橡胶衬套模型并导入到整车多体动力学模型中，但是通过有限元软件建立橡胶衬套的方法增加了工作量与研发周期。Dzierzek[6]基于试验数据提出了一种半经验参数模型，但模型没有描述扭转方向特性。

综上所述，国内外学者研究整车振动模型对车辆平顺性的影响时，建立的整车振动模型很少考虑到橡胶衬套力学特性模型，研究将橡胶衬套力学特性结合到整车模型中更加匮乏，这对平顺性分析有一定的影响。车辆是一个复杂的振动系统，在研究车辆平顺性时，整车振动模型通常采用七自由度模型。因此，本文通过构建橡胶衬套力学特性模型，建立引入橡胶衬套静态和动态力学特性模型的整车振动模型，通过MATLAB建立其数学模型并进行仿真，将经典七自由度振动数学模型与引入橡胶衬套静态、动态力学特性模型的整车振动数学模型对平顺性评价指标的影响进行对比分析，研究橡胶衬套对于车辆平顺性的影响。

1 橡胶衬套力学特性模型

通常橡胶衬套与频率相关的特性称为粘弹性，与幅值相关的特性称为弹塑性。目前，对于橡胶衬套动态特性的研究，学者均认为弹塑性和粘弹性是相互不关联的，可以对其模型单独进行分析。因此，本文通过对已有橡胶衬套的弹塑性和粘弹性模型进行分析，构建包含静态、动态力学特性的橡胶衬套模型。

1.1 橡胶衬套弹塑性模型

基于橡胶衬套的动态力学特性表现的摩擦迟滞特性，学者们在研究橡胶衬套动态力学特性时，普遍采用摩擦元件来描述摩擦迟滞，主要摩擦元件模型有：线性摩擦模型[7]、Bouc-Wen模型[8]等。其中线性摩擦模型系数少，结构简单，能够描述橡胶变形时摩擦力与相对位移的关系，但不能够描述瞬时摩擦。而Bouc-Wen模型是Wen基于Bouc模型进行修改提出的，通过使用一阶微分方程描述非线性光滑迟滞模型，其数学模型如式(1)所示。

式中：x（t）为衬套两端点相对位移；z（t）为模型迟滞恢复力；a为系统线刚度；γ、β为系统参数，影响系统非线性段的刚度与阻尼，β>0、γ<0，系统刚度非常小；β<γ迟滞曲线面积大，即系统耗能增加；γ<0，系统不稳定；n为系统参数。

Bouc-Wen模型中参数较多，通常采用最小二乘法进行参数识别。Bouc-Wen模型可以通过改变参数来获取多种不同形状的曲线，能够精确的描述橡胶非线性迟滞的力学特性，得到了广泛应用。因此，本文选取Bouc-Wen模型来描述橡胶衬套的幅值相关特性。

1.2 橡胶衬套粘弹性模型

橡胶衬套的粘弹性是通过动刚度和损耗角进行频率相关性描述。目前，通常描述橡胶衬套粘弹性的模型有：Kelvin-Voigt模型、三参数Maxwell模型和Frequency-Dependent模型。三种粘弹性模型的具体内容如表1所示。

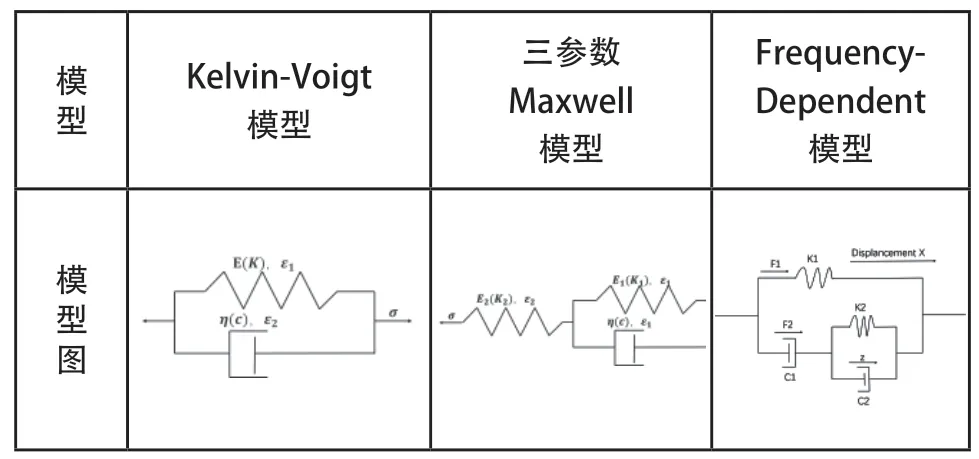
表1 粘弹性模型图

通过橡胶衬套的静态力学试验和动态力学试验，可得到橡胶衬套的线刚度、扭转刚度、动刚度以及损耗角等参数。

基于橡胶衬套的试验数据和粘弹性的三参数Maxwell模型、Kelvin-Voigt模型和Frequency-Dependent模型，分别对橡胶衬套的动刚度及损耗角进行拟合对比，其结果如图1～图3所示。图1～图3中，虚线为试验数据；实线为模型拟合曲线。

通过图1～图3可知，三参数Maxwell模型动刚度曲线拟合试验数据在低频时拟合较差，对于损耗角的拟合较差。Kelvin-Voigt模型能够较好的拟合损耗角试验数据，但是对于动刚度拟合较差。Frequency-Dependent模型对于动刚度及损耗角的试验数据拟合较好，但是在低频时的损耗角拟合有所差异。

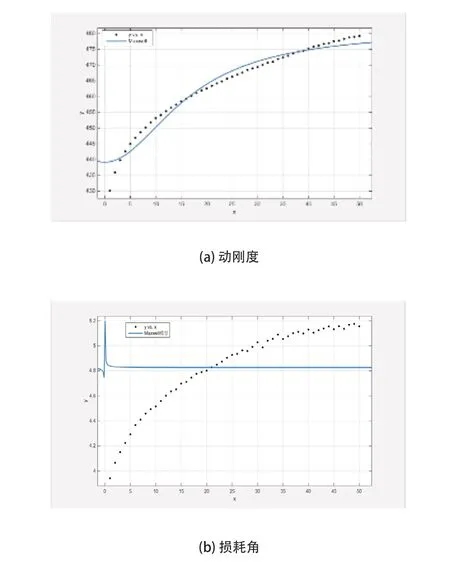
图1 三参数Maxwell模型动刚度与损耗角的曲线拟合图

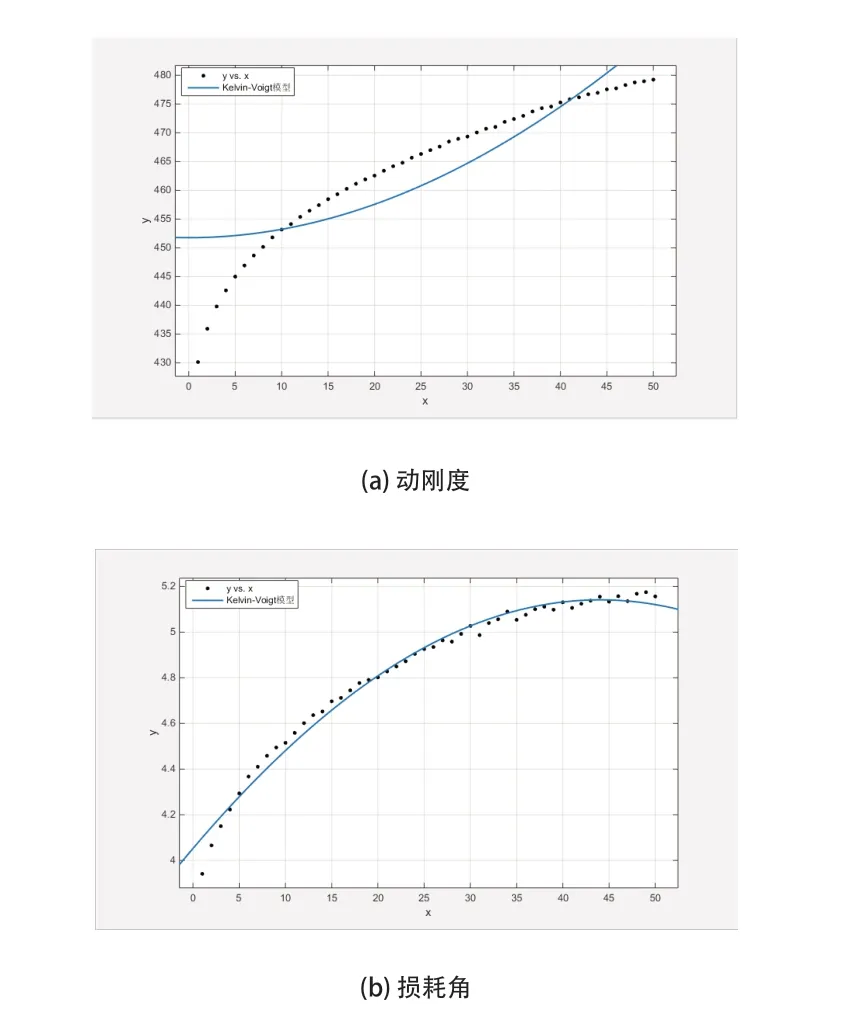
图2 Kelvin-Voigt模型动刚度与损耗角的曲线拟合图

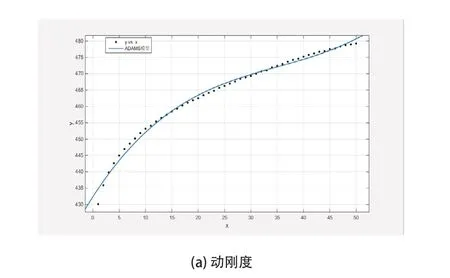
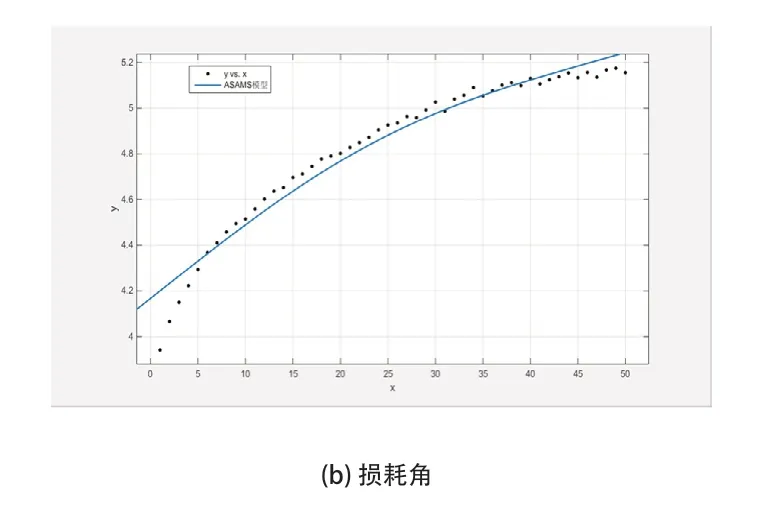
图3 Frequency-Dependent模型动刚度与损耗角的曲线拟合图

上述三种粘弹性模型的拟合结果表明，Frequency-Dependent模型对于橡胶衬套粘弹性的拟合效果最好。因此，本文选取Frequency-Dependent模型来描述橡胶衬套的粘弹性。

1.3 橡胶衬套力学模型构建

本文选取非线性弹性元件描述橡胶衬套的超弹性，Frequency-Dependent模型描述橡胶衬套粘弹性，Bouc-Wen模型描述橡胶衬套弹塑性，构建了包含静态、动态力学特性的橡胶衬套模型，如图4所示。

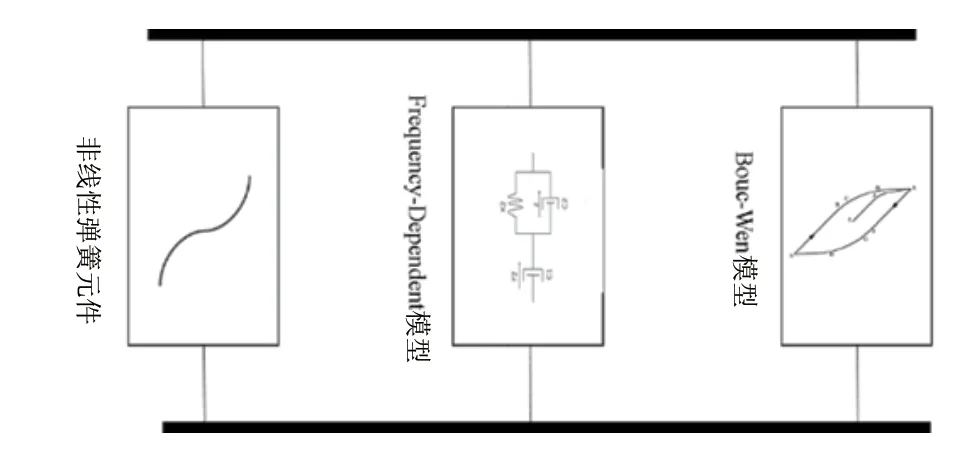
图4 包含静态、动态力学特性的橡胶衬套模型

模型中描述橡胶衬套粘弹性的Frequency-Dependent模型，其模型的输入为力，输出为位移，并且力与位移的关系为：

对式(2)进行拉氏变换与傅里叶变换得：

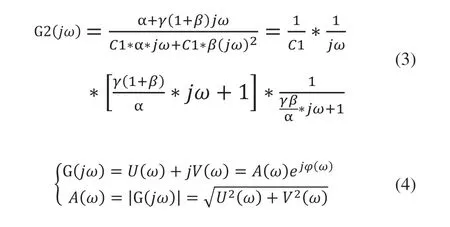
由式(3)与式(4)可以推导出Frequency-Dependent模型的动刚度与损耗角：

2 整车七自由度振动模型

2.1 经典七自由度振动模型

车辆立体模型中，车身、车架及其上总成所构成的车身质量为m1，车轮、车轴构成的车轮质量为m2。在分析车辆平顺性时，车辆立体模型的车身质量主要考虑垂直、侧倾及俯仰三个方向的自由度，车轮质量只考虑垂向的四个自由度，共七个自由度。车身具有绕通过质心x轴和y轴的转动惯量Ix、Iy。经典七自由度振动模型如图5所示。模型假设：

图5 经典七自由度振动模型

1）车辆行驶状态为匀速行驶，静平衡下的车辆位移为线性位移；

2）模型忽略轮胎阻尼，用等效刚度代替；

3）车辆簧载与非簧载质量视为刚体，且弹簧、减震器、轮胎位移可以通过刚度线性表示；

4）路面激励为垂向方向，车轮、减震器等只考虑垂向的运动、刚度等；

5）车辆左右对称。

图中：q1，q2，q3，q4为分别为路面激励；Z1，Z2，Z3，Z4分别为轮心位移；

m1，m2，m3，m4为分别为簧下质量；Kt1，Kt2，Kt3，Kt4分别为轮胎刚度；

Kd1，Kd2，Kd3，Kd4分别为悬架刚度；Cd1，Cd2，Cd3，Cd4分别为减震器阻尼系数；

Zb1，Zb2，Zb3，Zb4分别为簧下与簧上连接处垂直位移；

Z5为车身垂直位移；θ，φ分别为整车侧倾角、俯仰角；

mb为簧载质量；Ix，Iy侧倾转动惯量、俯仰转动惯量；

a、b分别为前、后轴至整车质心距离；L、d分别为轴距、轮距。

簧下与车身连接处垂直位移与速度：

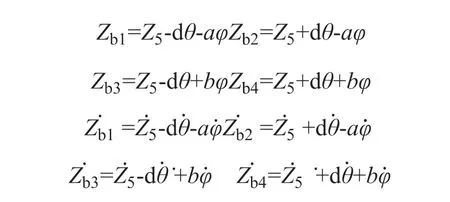
通过对图5振动模型进行受力分析，可得模型系统动能、势能和耗能如表2所示，进而通过对模型系统动能、势能和耗能公式进行拉格朗日变换可得方程组(5)。

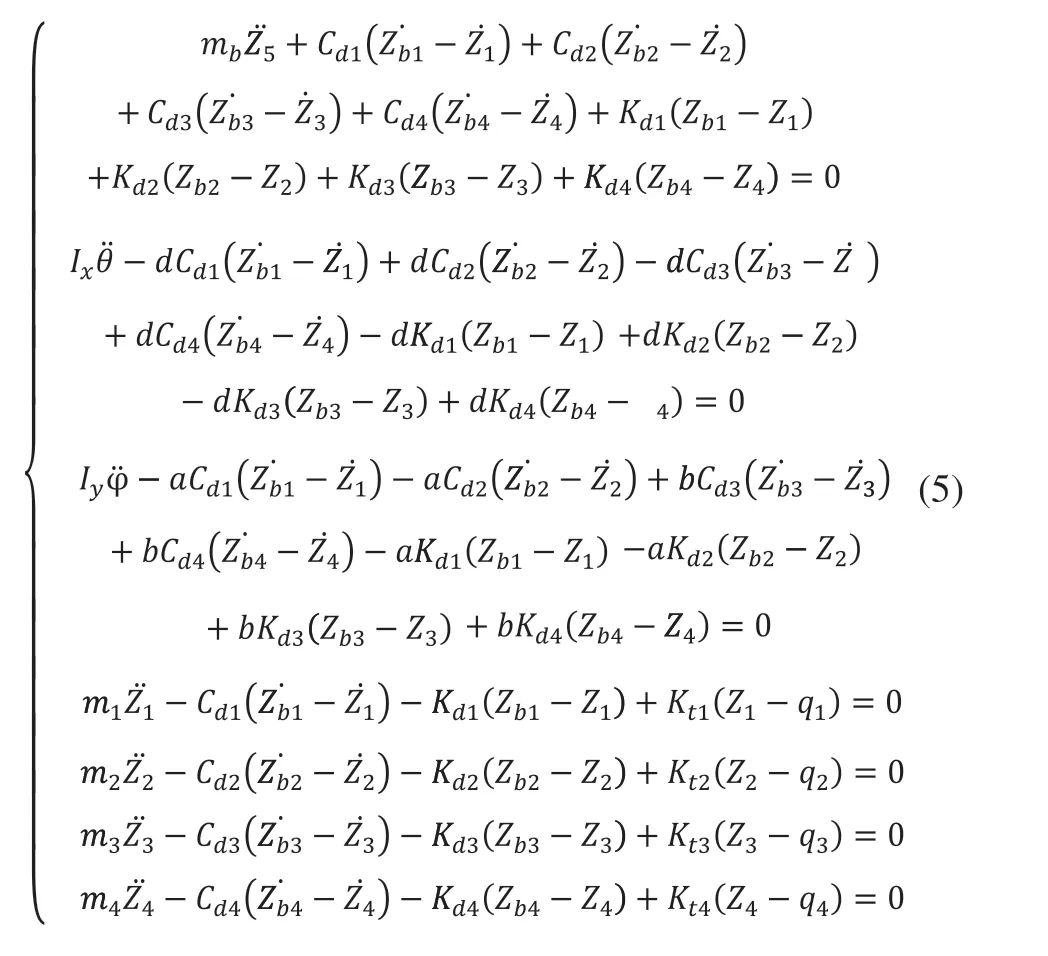
2.2 引入橡胶衬套力学特性模型的整车振动模型

基于整车经典七自由度振动模型，将橡胶衬套力学特性模型导入到整车振动模型中，建立引入橡胶衬套静态、动态力学特性模型的整车振动系统模型，其模型图如图6所示。模型中假设橡胶衬套的动刚度为Kz1，Kz2，Kz3，Kz4，阻尼为Cz1，Cz2，Cz3，Cz4，且模型左右对称。

图6中：Cb1，Cb2，Cb3，Cb4，Cb5，Cb6，Cb8，Cb1分别为橡胶衬套阻尼；Ks1，Ks2，Ks3，Ks4，Kn1，Kn2，Kn3，Kn1分别为橡胶衬套刚度。

表2 模型系统动能、势能、耗能公式表

通过对图6振动模型进行受力分析，可得到模型系统动能、势能和耗能如表3所示，其中U1、U2、U3、U4表示橡胶衬套的势能，R1、R2、R3、R4表示橡胶衬套的耗能。

表3 模型系统动能、势能、耗能公式表

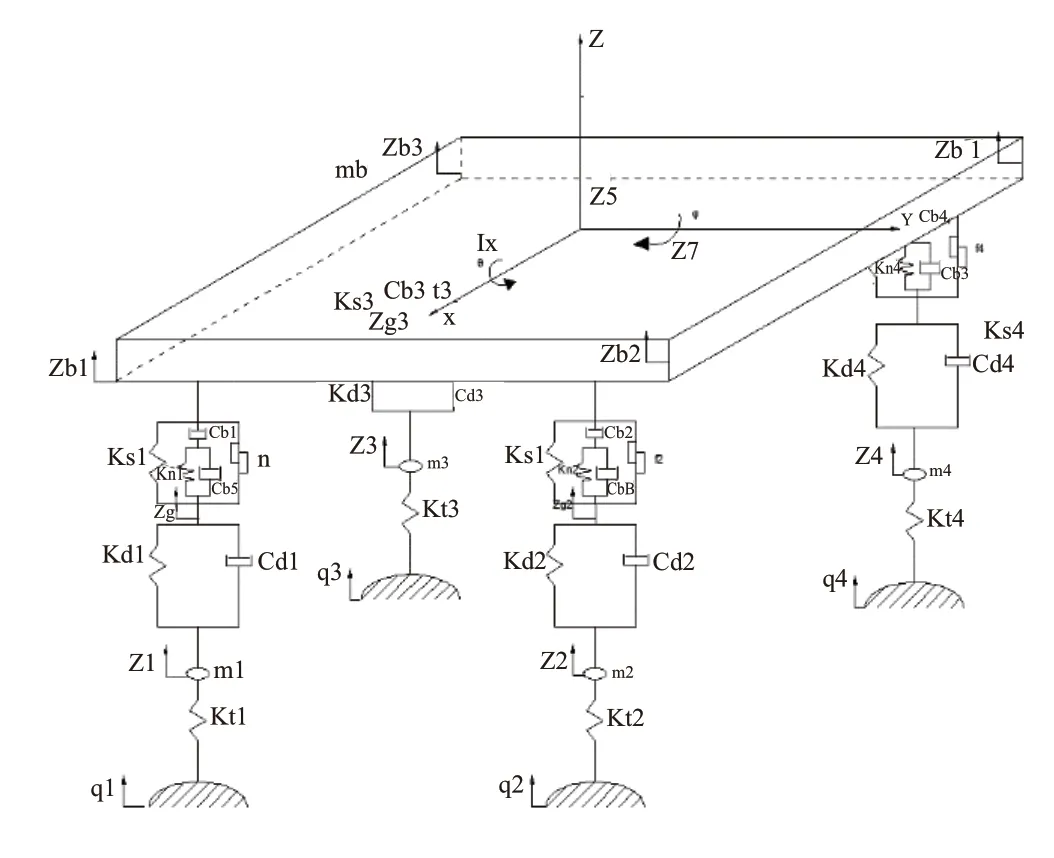
图6 引入橡胶衬套力学特性模型的整车振动模型

通过对表3中模型系统动能、势能和耗能公式进行拉格朗日变换可得方程组6，将方程组整理成微分方程形式，可推导出X、Q、M、K、C，可以较为精确的描述悬架系统中零部件对于车辆平顺性的影响。

3 模型仿真验证及试验对比分析

3.1 车型参数

依据试验车型SUV，在MATLAB中建立两种模型的数学仿真模型进行仿[9]，试验车型参数如表4所示。其中前后悬架分别采用麦弗逊式独立悬架和多连杆式独立悬架；车身刚度采用橡胶衬套进行模拟，橡胶衬套位置位于车身弯曲变形最大处；轮胎采用F-tire模型，轮胎规格235/55R18。

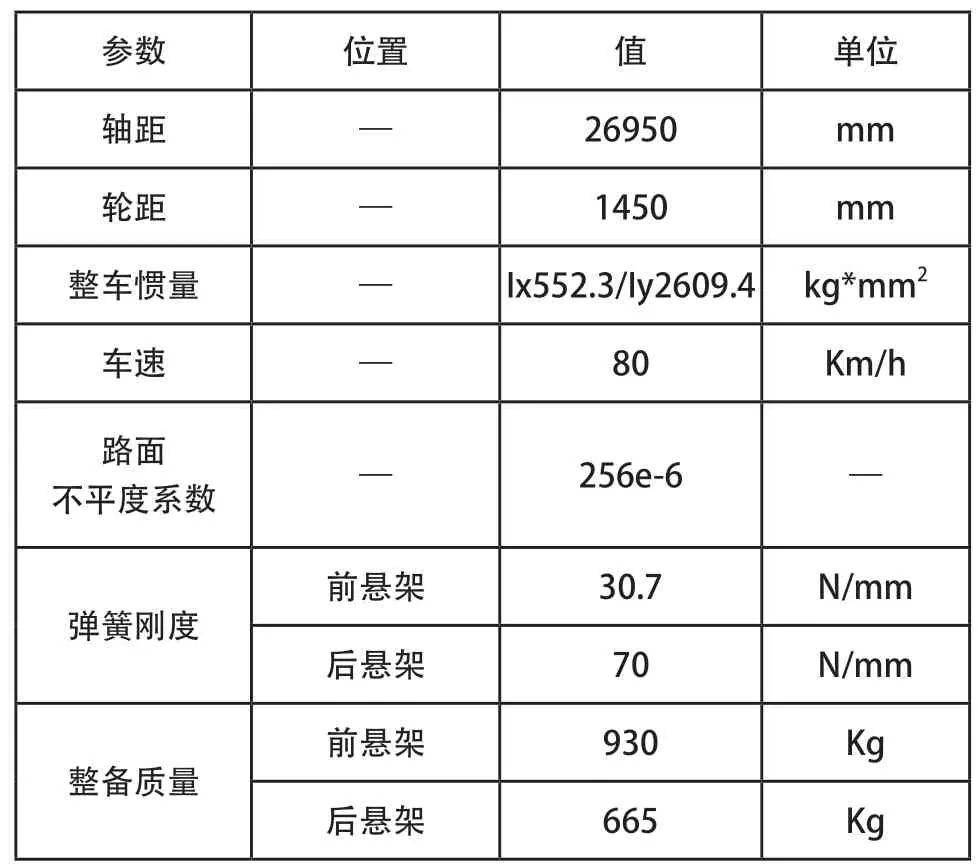
表4 SUV车型整车参数

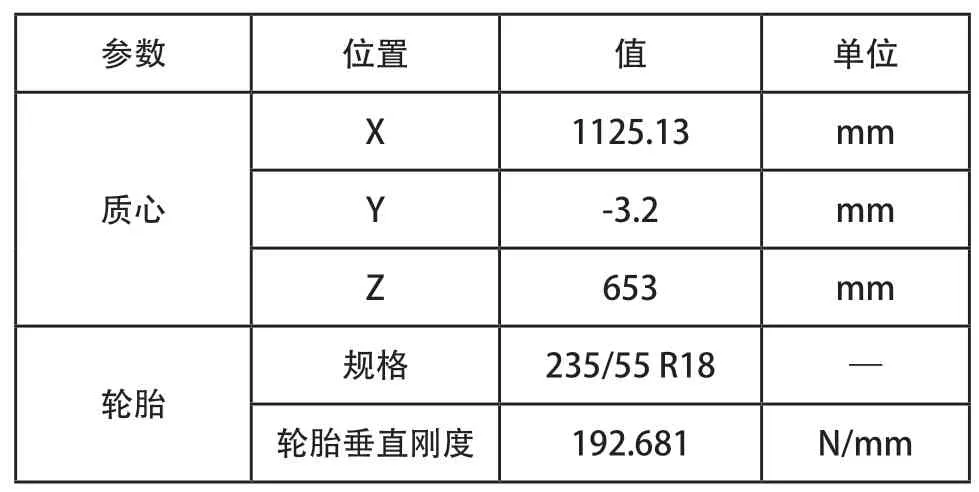
表4 （续）

3.2 模型仿真验证

车辆行驶时的车身垂向加速度、车轮处垂向加速度和悬架弹簧动挠度是车辆平顺性评价的重要指标。在MATLAB中建立的引入橡胶衬套静态、动态力学特性模型的整车振动模型，只考虑了前悬架下摆臂后衬套的模型。并且本文采用整车七自由度振动系统模型进行分析，选用车身与车轮双质量系统的振动模型分析其平顺性指标。

稳态系统的响应z由激励q以及频率传递特性确定，其频率响应函数为H（jω）z～q：

将复振幅代入振动系统的微分方程组，得到七自由度振动模型的频率响应函数，通过响应函数推导得：悬架动挠度fd与q的频率响应函数以及车身加速度z5与q的频率响应函数：

通过平顺性系统框架的输入与振动分析，在MATLAB中建立经典七自由度数学模型与引入橡胶衬套静态、动态力学特性模型的整车数学模型，对车身处加速度功率谱密度、车轮处加速度功率谱密度、悬架动挠度进行振动响应对比分析，其结果如图7～图9所示。

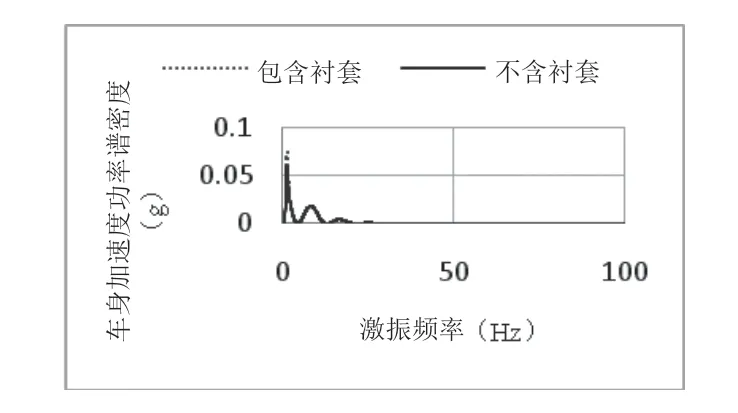
图7 车身垂直加速度功率谱密度曲线

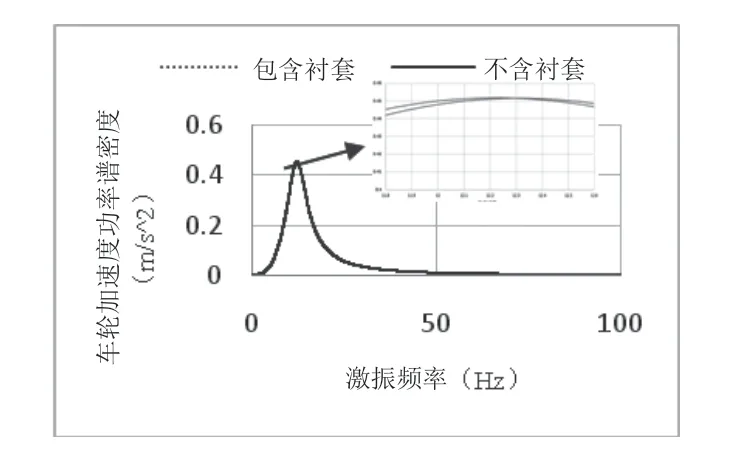
图8 前悬架车轮垂直加速度功率谱密度曲线

由图7～图9可得，经典七自由度振动模型所得到的车身固有频率为1.3Hz，车轮处的固有频率为12.2Hz，引入橡胶衬套静态、动态特性的整车振动模型所得到的车身固有频率为1.4Hz，车轮处的固有频率为12.29Hz[10]。

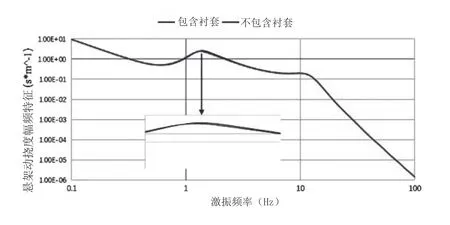
图9 前悬架动挠度幅频特性曲线

为了满足车辆具有良好的平顺性，在底盘设计开发时，要求车身处的固有频率范围为1Hz～2Hz，车轮处的固有频率范围在10Hz～15Hz之间，并且尽可能较低，两模型数据均符合设计规范，验证了建立的引入橡胶衬套静态、动态力学特性模型的整车振动模型的准确性。

3.3 试验对比分析

针对SUV试验车型，本文进行了车辆平顺性试验，其试验道路平直，纵坡小于1%。试验采用GB/T 4970-2009《汽车平顺性试验方法》中的标准。通过对试验车型SUV进行平顺性试验和计算，可得试验车型SUV的前悬架偏频结果，如图10、图11所示。由图10和图11计算可得车身和车轮固有频率，与3.2节中仿真结果如表5所示。

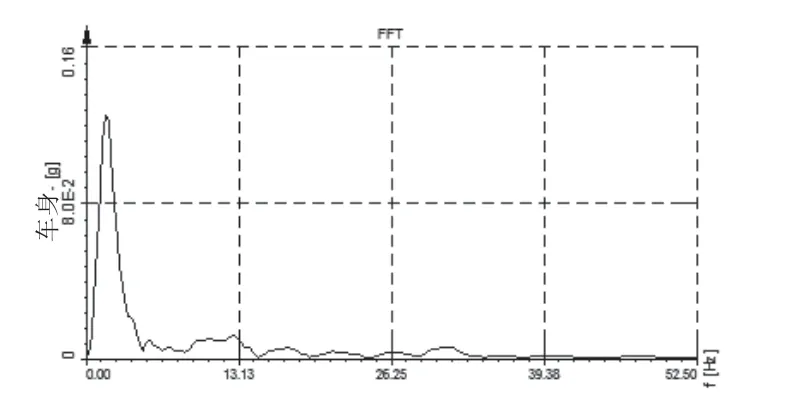
图10 试验车型车身垂直加速度功率谱密度曲线

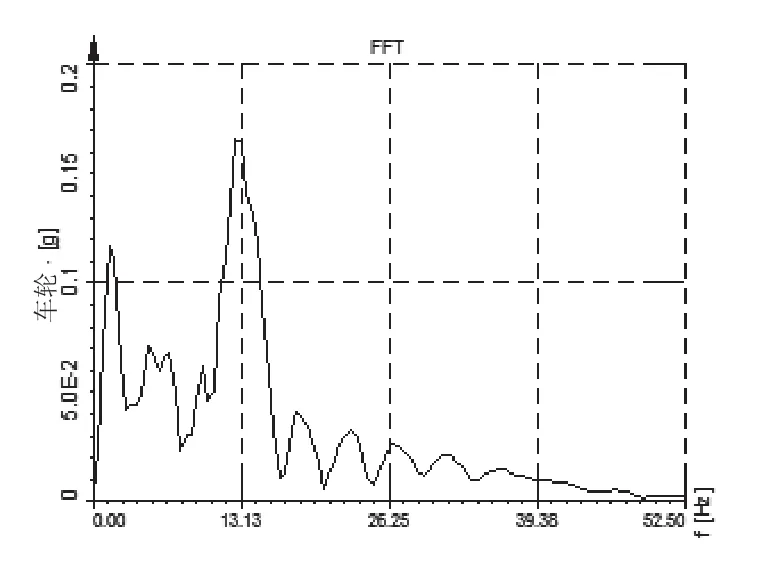
图11 试验车型前悬架车轮垂直加速度功率谱密度曲线

由表5分析可得，基于整车经典七自由度振动模型，在整车中加入前悬架下摆臂后衬套，得到的引入橡胶衬套静态、动态力学特性模型的整车振动模型的偏频值有一定的增大，更加符合试验值，结果表明，建立的引入橡胶衬套静态、动态力学特性模型的整车振动模型能够更精确的描述车辆的振动传递特性。

表5 车身及车轮处固有频率对比

4 结语

1）本文分析了橡胶衬套粘弹性与弹塑性的模型，并且通过推导模型动刚度与损耗角来描述橡胶衬套力学特性，构建了包含静态、动态力学特性的橡胶衬套模型。

2）基于整车经典七自由度振动模型，构建了引入橡胶衬套静态、动态力学特性模型的整车振动模型，通过MATLAB建立其数学模型并进行了仿真分析，验证了引入橡胶衬套静态、动态力学特性模型的整车振动模型的准确性。

3）对整车经典七自由度振动模型与构建的引入橡胶衬套静态力学特性和动态力学特性模型的整车振动模型进行平顺性评价指标分析，并与试验数据进行对比分析，确定了引入橡胶衬套静态、动态力学特性模型的整车振动模型能够更精确的描述车辆的振动传递特性。