一种面向管道堵塞不均衡样本集的主动学习方法

王显龙 冯 早 赵燕锋

（昆明理工大学a.信息工程与自动化学院；b.云南省人工智能重点实验室）

随着城市建设的快速发展，排水系统成为城市生态物质循环代谢系统的重要一环，正常运行的排水系统起到保护城市环境、提高居民健康水平以及维持城市交通正常运转的作用［1］。近年来，城市内涝灾害频发，排水系统堵塞故障检测的重要性也日益凸显［2］。

因为声波不仅能在空气中传播，还能在固体、液体和气体介质中传播，所以声波作为一种无损检测技术检测排水管道的堵塞故障具有独特优势［3］。利用统计学习方法，对管道内的声波信号进行有效预处理和特征提取，便可实现对管道运行状态的识别。

随着大数据和人工智能技术的发展，机器学习在故障诊断领域的应用越来越广泛，目前基于数据驱动的管道故障识别大多采用监督学习方法。焦敬品等采用BP神经网络对管道泄漏声发射信号进行识别，整体识别率达到了92.5%［4］。伍林峰等采用小波包稀疏表征分类方法对管道堵塞情况进行识别，获得了96.88%的准确率［5］。郎宪明等采用K均值欠采样方法处理不均衡管道数据集，结合改进的双支持向量机快速识别管道泄漏孔径并定位泄漏位置［6］。然而，基于监督学习方法的管道检测识别模型需要大量的已标注数据样本训练模型，这定会增加管道检测数据样本的标注成本。为此，仅在标注少量管道数据样本的情况下，训练高效且泛化能力强的管道堵塞识别分类模型至关重要。此外，排水管道的正常数据样本量和堵塞数据样本量存在严重的数据不均衡问题，若以传统的监督学习方法分类识别模型，会造成严重的堵塞故障的漏诊和误判。

主动学习通过从未标注样本集中挑选信息度高的样本，经标注后补充到训练集中，从而提升分类模型的性能［7］。为了筛选未标注样本，Tong S和Koller D用不确定性度量的采样策略筛选最靠近分类边界的样本［8］；陈念和唐振民采用QBC委员会的样本采样策略的主动学习模型对垃圾邮件进行在线过滤，降低了标注成本和时间成本，但是该方法并没有考虑数据不均衡对分类结果的影响［9］；毛蔚轩等用基于经验风险最小化的主动学习方法对恶意代码进行检测，实现了5.55%的低错误率，但是该方法严重依赖网络数据，不具有通用性［10］。

笔者针对排水管道堵塞数据集中存在的严重的数据不均衡现象，提出基于分类熵和余弦相似度的样本采样策略和极限随机树的主动学习堵塞故障识别方法。

1 声波信号检测管道堵塞原理

管道中传播的声波，其特点是声波被约束在管道里，没有扩散，可以传播得很远［11］。在管道内部，声波遇到堵塞物被反射回来，使得管内声场形成驻波声场。设Pi为入射检测声波声压，则有：

式中 c0——声波的传播速度；

k——波数；

P0——声源振动产生的入射声波声压；

t——声波传播时间；

x″——声波传播距离；

ω——声源简谐振动的圆频率。

设堵塞物的声压反射系数为r，则反射声波声压Pr的数学表达式为：

如果声波在含有旁支的管道中传播，由于旁支口的影响，主管道中将产生反射波，旁支管道产生漏入波，入射波有可能穿过旁支口产生透射波。

根据声压连续条件，可得反射波、入射波、漏入波和透射波之间的声压关系式为：

式中 Pb——漏入波声压；

Pt——透射波声压。

如图1所示，声波在管道内传播，由于振动的空气质点之间的摩擦，使得一小部分声能转化为热能，称为空气对声能的吸收。声波遇到堵塞物，堵塞物吸收部分声能。部分声波绕过堵塞物发生衍射，这部分声能穿过堵塞物传递到堵塞物的另一端。基于以上现象，只要检测声场相关物理量的变化就可以实现对管道运行状况的识别。

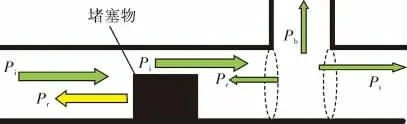
图1 声波在管道内的传播示意图

2 变分模态分解与特征提取

2.1 变分模态分解

传统的傅里叶分析用一系列三角基函数对信号进行正交运算，但是管道内部情况复杂，采集到的往往是非线性、非平稳信号。若以傅里叶分析信号，得到的只是某一段时间内频率的均值，无法准确描述频率随时间的变化［12］。虽然希尔伯特-黄变换能够自适应地处理非平稳随机信号［13］，但 是 经 验 模 态 分 解（Empirical Mode Decomposition，EMD）方法存在不能分解低能量模态和产生虚假模态分量的明显缺陷［14］。变分模态分解（Variational Mode Decomposition，VMD）是一种自适应、完全非递归的模态变分和信号处理方法，该方法克服了EMD方法存在端点效应和模态分量混叠的问题，并且具有更坚实的数学理论基础，可以降低复杂度高和非线性强的时间序列的非平稳性，分解获得包含多个不同频率尺度且相对平稳的子序列，适用于非平稳性序列［15］。VMD的优点在于它能够根据实际情况确定所给序列的模态分解个数，在随后的搜索和求解过程中可以自适应地匹配每种模态的最佳中心频率和有限带宽，并且可以实现固有模态分量（IMF）的有效分离和信号的频域划分，进而得到给定信号的有效分解成分，最终获得变分问题的最优解。VMD首先构建和求解变分问题，假设原始信号f（t）被分解为N个量，保证分解序列是具有中心频率的有限带宽的模态分量，同时各模态的估计带宽之和最小，约束条件为所有模态之和并与原始信号相等，相应的约束变分表达式为：

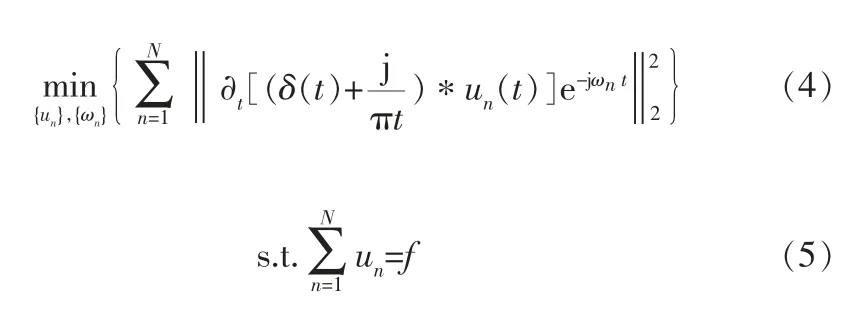
其中，N为指定分解的模态分量个数，*表示卷积运算，un、ωn分别为第n个模态分量和中心频率。

为了降低噪声干扰并求解式（5），引入拉格朗日算子λ和二次惩罚因子α，得到增广拉格朗日表达式：

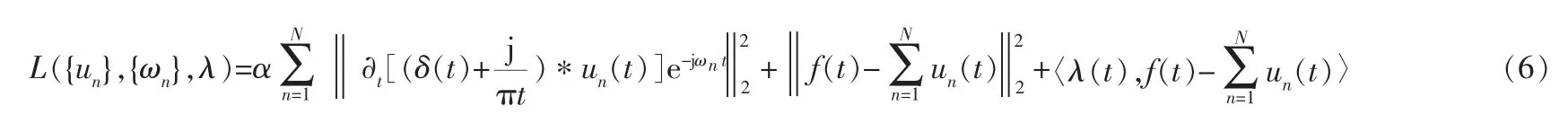
利用交替方向乘子 （Alternating Direction Method of Multipliers，ADMM）迭代算法、傅里叶等距变换优化得到各模态的分量和中心频率，并搜寻增广拉格朗日表达式（5）的鞍点，交替寻优迭代后分别更新un、ωn和λ：

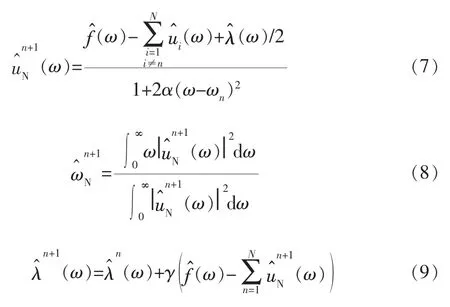
2.2 特征提取

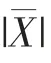
模糊熵的大小衡量了时间序列信号复杂度的大小，其计算步骤如下：

a.假设一个时间序列X（i），i=1，2，…，n′；

b.以m为窗，将时间序列X（i）分为k′=n′-m+1个序列，Xi（t）=（Xi（t），Xi+1（t），…，Xi+m-1（t））；

c.计算每个序列与所有k′个序列之间的距离d，并列表dij=max｜Xi+k′（t）-Xj+k′（t）｜，其中k′=0，1，…，m-1；

e.将窗m增长为m+1，重复步骤b～d；

f.计算模糊熵FuzzyEn（t）=lnφm（t）-lnφm+1（t）。

3 基于主动学习模型的管道堵塞故障识别

大多数的监督机器学习模型都需要基于大量数据的训练才能取得良好的效果，尤其是带有“标注”的数据，是监督模型的关键，制约着监督模型的学习效果。大多数情况下，相关领域专家获得的是一个庞大的、未经标注的数据集。然而，数据的标注工作费时费力且成本高昂。为了尽可能地减少训练集和标注成本，主动学习在机器学习领域应运而生。主动学习可以主动地提出数据标注请求，将一些经过筛选的数据提交专家进行标注，筛选数据的依据是数据的信息度。如图2所示，主动学习过程分为两个阶段：

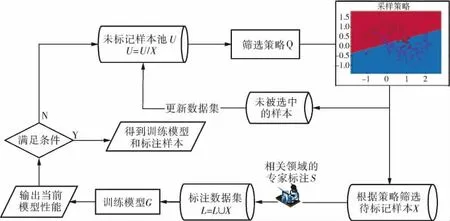
图2 主动学习过程

a.初始化阶段。从未标注的样本中随机选取小部分数据，由督导者标注作为训练集L，剩余未标注样本集为U，建立初始分类模型。

b.循环查询阶段。从未标注样本集中按照查询策略Q选取一定数量的样本进行标注，并更新已标注样本集L和未标注样本集U，重新训练分类器直至达到训练停止标准为止。

3.1 基于分类熵和余弦相似度的样本查询策略

样本信息指的是在训练数据集中每个样本带给模型训练的信息是不同的，即每个样本为模型的训练的贡献是有差异的。从未标注样本中集中筛选样本，衡量样本信息量差异的方法主要有不确定性标准、版本空间缩减标准和泛化误差缩减标准［17］。为了度量模型对未标注样本分类的确定性，引入熵的概念，熵可视为系统中无序性的度量。如果模型对给定数据点的类别具有高度的确定性，则对于特定类可能具有较高的确定性，而所有其他类的可能性都比较低。在高熵的情况下，意味着该模型将概率近似地分配给所有类别，因为模型根本不确定该数据点属于哪个类别，这与使气体均匀分布在盒子的所有区域的情况相似。因此，具有较高熵的数据点较具有较低熵的数据点应该有更高的优先级被筛选出来提交人工标注。分类熵SE的定义如下：

使用分类熵（或其他类似策略）抽样时，无法考虑数据的结构分布信息，这将导致进入次优查询。为了缓解这种情况，一种方法是使用信息密度度量帮助指导查询。余弦相似性通过测量两个向量的夹角的余弦值来度量它们之间的相似性。从样本集U中，采用样本筛选策略构建待标注的数据集Xu，从中筛选的样本x的信息密度I（x）可计算为：

其中，x′表示已标注样本。

在筛选样本时，为了同时考虑样本的不确定性和代表性，笔者选择分类熵和余弦相似度相结合的方式求其最大值实现样本查询策略来筛选未标注样本，即arg max（SE+I（x））。

3.2 基分类器——极限随机树

极限随机树算法与随机森林算法十分相似，都是由许多决策树构成的［18］。随机森林的多个决策树都是互相独立的，并且不需要进行“剪枝”操作。在训练过程中，每棵决策树采用有放回采样方法构造新的训练数据集，在一个随机子集内得到最佳分叉属性。相较于传统的集成学习方法，随机森林能较好地容忍噪声且稳定性较高。极限随机树应用的是Bagging模型，极限随机树使用的所有的样本，只是特征是随机选取的，其主要过程为：当特征属性是类别的形式时，随机选择具有某些类别的样本为左分支，而把具有其他类别的样本作为右分支；当特征属性是数值的形式时，随机选择一个处于该特征属性的最大值和最小值之间的任意数，当样本的该特征属性值大于该值时作为左分支，当小于该值时作为右分支。这样就实现了在该特征属性下把样本随机分配到两个分支上的目的。然后计算此时的分叉值，如果特征属性是类别的形式，采用基尼指数；如果特征属性是数值的形式，采用均方误差。遍历节点内的所有特征属性，按上述方法得到所有特征属性的分叉值，并选择分叉值最大的形式实现对该节点的分叉。

综上所述，极限随机树相较于随机森林有两个优点：首先极限随机树可以减少偏差；其次极限随机树中每棵决策树的分裂阈值是完全随机选择的，可以减少方差。因此，笔者提出以极限随机树为基分类器，结合分类熵和余弦相似度的样本查询策略，建立主动学习模型，以实现对排水管道堵塞故障数据集在不均衡情况下的分类识别。

4 试验方案设计与数据采集

为了模拟排水管道的运行情况，笔者设计了排水管道模拟试验平台（图3），PVC排水管道的总长度为15.4m、管道的直径1为50mm，管道分为3段，分别设置为空管区域、管道堵塞区域和管道三通件区域。循环水泵和水箱控制管内水位保持较低水位的流动。试验平台中的计算机安装WinMLS软件，并驱动声卡产生时间为10s、频率范围100～6 000Hz的正弦扫频信号作为检测声波信号，检测声波信号由扬声器释放到管道内部。由于扬声器发出的不一定是纯音，所以必须在接收端进行滤波，去除不必要的高次谐波分量。四通道传声器采集管道内部信号，传声器的采样频率设置为44 100Hz，经放大器放大后上传至计算机做进一步处理。

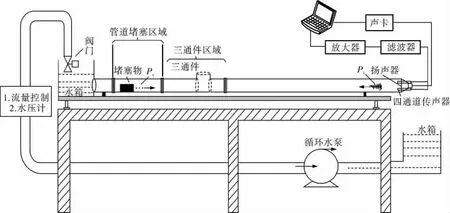
图3 排水管道模拟试验平台

管道堵塞程度设置与管道直径的比例存在一定关系，定义堵塞物高度在管道直径的1/3以下为轻度堵塞，堵塞物高度超过管道直径的1/3为中重度堵塞。本试验用20mm障碍物模拟轻度堵塞，55mm障碍物模拟中重度堵塞。试验采集无堵塞直管、轻度堵塞、中重度堵塞和含三通件正常管道4种管道运行状态信号数据，时域信号如图4所示。为了模拟管道堵塞故障类别不均衡程度，试验方案设置两组数据的类别数量比例分别置为1.0∶1.0∶0.3∶0.2和1.0∶1.0∶0.2∶0.1，两组数据分别模拟不同的数据不均衡程度，第1组数据和第2组数据的总数分别为250和210。

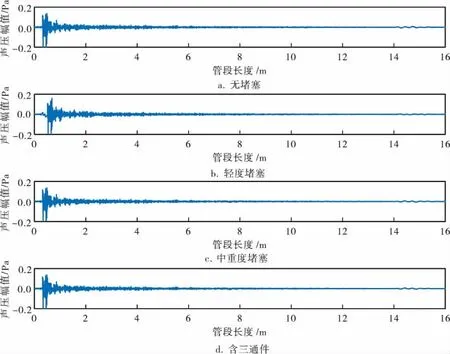
图4 4种管道运行工况下的时域信号

为了提取信号的有效特征表征不同的类型数据，需要对采集到的时域信号进行特征提取。特征提取的主要过程是：先对信号进行变分模态分解，根据模态分量的中心频率选择分解个数为4［19］。以无堵塞直管运行状态时域信号为例，其分解结果如图5所示。

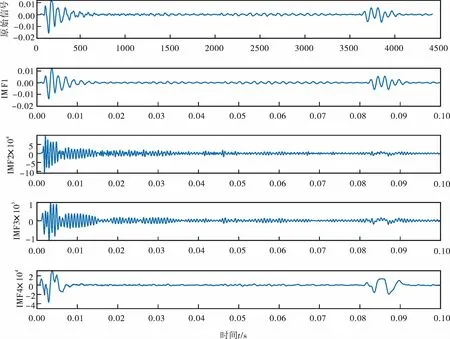
图5 无堵塞直管时域信号变分模态分解结果

由于原始信号经由变分模态分解后得到4个模态分量，分别计算这4个模态分量的脉冲因子和模糊熵，其中模糊熵嵌入维数越大时越能更细致地重构系统的动态演化过程，本试验选取嵌入维数为4［19］。信号的最终特征提取结果见表1、2。

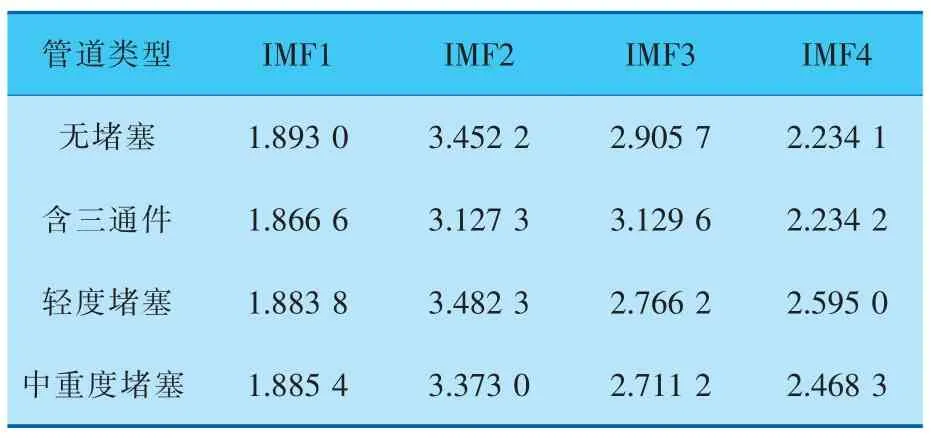
表1 脉冲因子特征提取结果

5 试验与分析

为了验证基于极限随机树的主动学习模型对排水管道堵塞故障识别的有效性，基于试验平台选取两组试验数据。根据故障类数据所占总数据的比例，定义数据集一为普通不均衡数据集，数据集二为极端不均衡数据集。设置两组数据集的不均衡比例变换主要是为了检测主动学习方法的有效性。初始已标注训练集为12个样本，各类别的样本个数分别为4、4、2、2，主动学习过程中，样本查询次数均为20次。

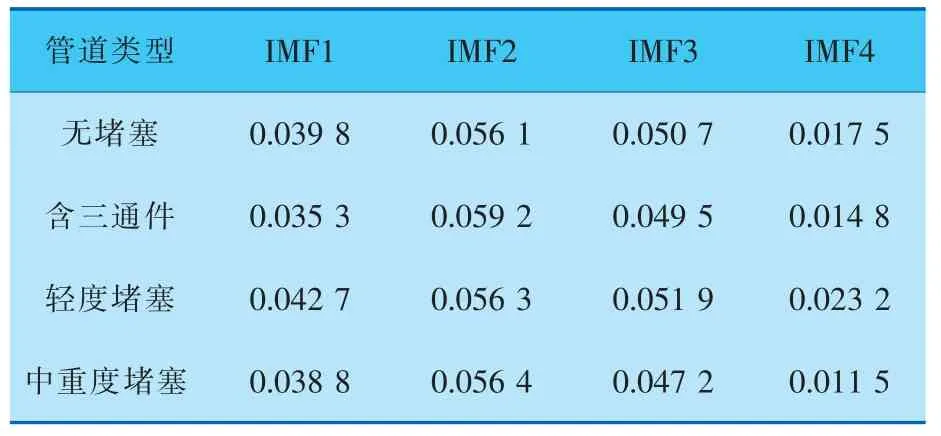
表2 模糊熵特征提取结果

为了检验基于极限随机树的主动学习模型对管道堵塞故障的识别能力，通过绘制模型的学习曲线和混淆矩阵进行比较。排水管道堵塞识别主动学习模型如图6所示，首先在信号采集完成之后利用已标注样本训练集训练排水管道堵塞故障分类识别模型——极限随机树，然后在已有分类模型的基础上使用分类器评价剩余未标注样本并对选择出的待标注信号进行样本标注，其次更新已标注的训练集和未标注的训练集，如果分类模型的输出精度符合要求则停止迭代训练过程并输出最终结果。

图6 排水管道堵塞识别主动学习模型

5.1 初始分类模型对未标注样本集测试结果的分析

笔者所提分类模型对数据集一的初始识别结果如图7所示，可以看出，在相同大小的已标注训练集下得到的模型，在普通不均衡数据集下得到的测试准确率略高于在极端不均衡数据集下的测试准确率。

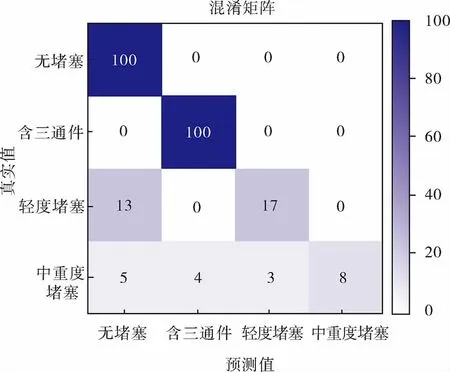
图7 分类模型对数据集一的初始识别结果

本试验中，由于管道堵塞故障数据集是不均衡的，对数据集分类识别时更应该看重少数类数据样本的分类结果。因此，笔者选择混淆矩阵来判断模型对少数类样本的识别效果。分类模型对数据集二的初始识别结果如图8所示，可以看出，在进行未标注样本采样之前，由于训练样本较少，在普通不均衡数据集上，模型对少数类堵塞故障样本的分类识别准确率不理想，随着堵塞故障的少数类样本进一步减少，模型在极端不均衡数据集中，对堵塞故障的识别效果进一步降低，出现了对中重度堵塞故障全部识别错误的情况。这是因为一般分类模型在对少数类样本进行分类识别时，往往以最小经验风险为优化原则，忽视了少数类样本。在对未标注样本集进行筛选采样之前，虽然模型对管道运行状态的识别均达到了90%以上的正确率，但是把堵塞类故障判别为正常类管道样本会造成更加严重的后果。为了避免主动学习过程对少数类样本的错误分类，从未标注样本集中选取样本进行标注，是提高堵塞故障少数类样本识别准确率的关键。

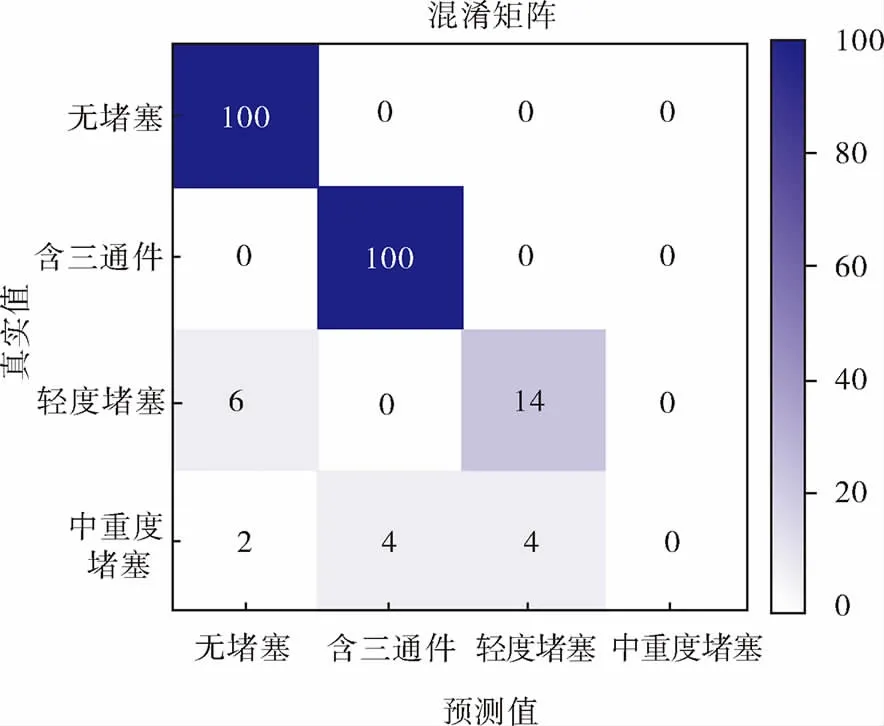
图8 分类模型对数据集二的初始识别结果

5.2 主动学习模型分类性能分析

主动学习模型在两个数据集的学习曲线如图9所示，可以看出，笔者提出的方法在普通不均衡数据集和极端不均衡数据集上分别取得了97.6%、97.8%的准确率，即使数据集中的不平衡比例增大，也没有影响笔者所提方法的准确率。

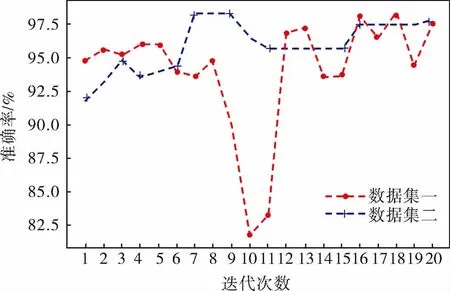
图9 主动学习模型在两个数据集的学习曲线

本试验的样本筛选策略主要考虑了分类模型对已筛选待标注样本的分类不确定性。同时，为了避免少数类样本对分类结果造成影响，通过余弦距离计算待标注样本与已标注样本集中各类别样本的特征距离，以衡量样本之间的相似程度，这在很大程度上改善了分类器对标注样本集中少数类别样本的误判。

分类模型在普通不均衡数据集的最终识别结果如图10所示，可以看出，数据集一的最终分类结果与模型初始分类结果相比，经过20次的未标注样本迭代查询后轻度堵塞中有3个样本被误分类为无堵塞管道，中重度堵塞类样本中有1个样本被误分类为无堵塞管道，2个中重度堵塞样本被误分类为含三通件管道。

分类模型在极端不均衡数据集的最终识别结果如图11所示，可以看出，数据集二的最终分类结果与模型初始分类结果相比，轻度堵塞类别样本中仅有5个样本被误分类为无堵塞管道，中重度堵塞样本全部分类识别正确。

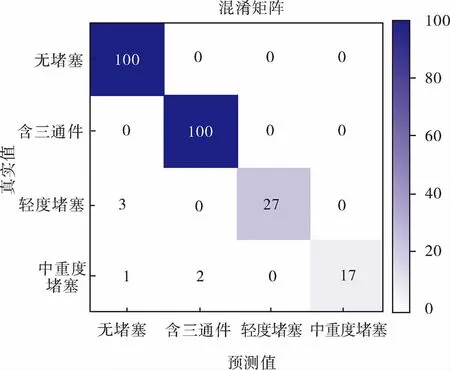
图10 分类模型在普通不均衡数据集的最终识别结果

5.3 查准率、查全率和F1度量值分析

根据图10、11可以得到笔者所提模型在普通不均衡数据集和极端不均衡数据集上的分类指标查准率P、查全率R和F1度量值。其中F1度量值由查准率和查全率计算得到，即：

其中，β为可调参数，通常取1。

可以看出，F1度量值与查准率P、查全率R成正比，F1度量值越大说明分类模型对少数类的分类效果越好。

根据图10、11可以得到笔者所提主动学习模型在普通不均衡数据集和极端不均衡数据集上的分类指标，结果见表3、4。可以看出，主动学习模型对中重度堵塞少数类样本的识别效果有了很大的改进。但相对于中重度堵塞，样本数量较大的轻度堵塞的F1度量值降低了，经分析，造成该后果的原因可能是在减少轻度堵塞样本的数据量时破坏了原始样本分布信息。

表3 普通不均衡数据集的分类指标

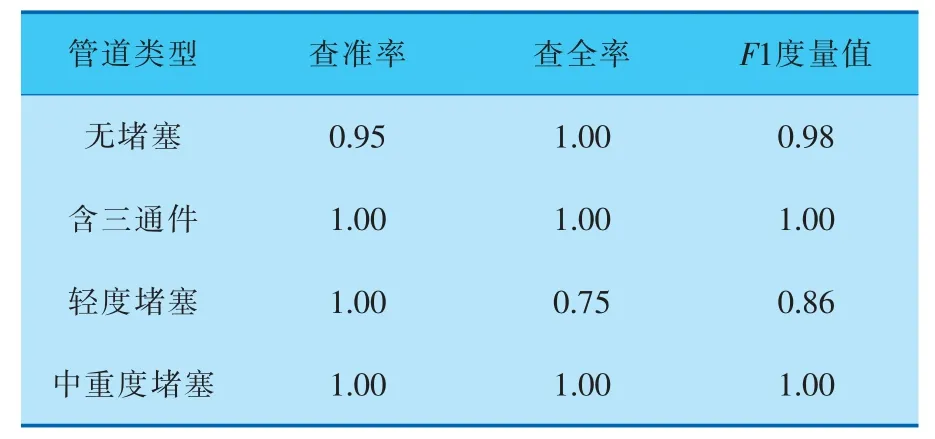
表4 极端不均衡数据集的分类指标

6 结束语

为了在排水管道堵塞故障检测过程中减少人工标注的负担，笔者提出了基于主动学习的排水管道堵塞故障识别模型。同时考虑到数据不均衡对分类结果造成的影响，改进了在主动学习过程中的样本查询策略。为了避免主动学习过程中数据不均衡给分类结果造成的不良影响，提出将衡量样本分类不确定性的分类熵和样本分布信息的余弦相似度相结合的样本查询策略，该策略在样本查询选择过程中考虑了未标注样本集中的少数类样本。试验在两组不均衡比例不同的数据集进行验证：在样本标注成本上，本试验以仅标注32个样本的标注成本在两个不均衡比例不同的数据集进行识别验证，均取得了较好的准确率，并极大地节省了人工标注样本的成本，而且笔者提出的主动学习模型能够显著提高少数类样本的F1度量值。

由于本试验考虑的试验条件是基于一个堵塞物，而在实际管道检测条件下，排水管道内部情况很复杂，大多数情况下会出现多重堵塞的管道，有些更加复杂的管道堵塞样本的数量更为稀少，因此，笔者提出的方法在更为极端的数据不均衡情况下还需更近一步验证。