基于激光超声二次谐波法检测混凝土早期损伤
许颖,郑倩,曹宇萌
(哈尔滨工业大学(深圳)土木与环境工程学院,广东 深圳 518055)
在役结构中的混凝土随着服役时间的增长,已大多处于早期损伤累积阶段,一旦结构出现明显损伤,结构的承载力将大幅度降低[1],因此对混凝土结构的早期损伤评估非常重要.混凝土的损伤往往都伴随着内部微观结构的变化,即裂缝的萌生以及开展[2].因此采取何种方法检测出混凝土内部微细观结构变化是国内外学者研究的重点.
激光超声检测技术因具有非接触、空间分辨率高和探测距离远等优点,近年来被广泛应用在制造业、建筑工程、航空航天及其他工业领域.早期的激光超声无损检测技术主要是利用激光在裂纹远场激发超声,通过探测超声波与裂纹作用产生的反射和透射信号来确定裂纹的存在[3-5].但由于位置未知的微小裂纹易受到声波波长的限制,导致只有很少一部分超声信号会被反射,因此该方法的检测效果会大幅降低.近年来兴起的非线性激光超声检测方法是通过观测由裂纹闭合作用产生的谐波、亚谐波或调制波等非线性声学现象,来实现对材料中缺陷的检测.相比于传统的线性激光超声检测方法,非线性激光超声检测方法有着更高的检测灵敏度,可用来检测开口更小的裂纹[6-7].为充分发挥非线性激光超声在结构材料无损检测中的作用,并克服传统超声换能器接触式工作的局限性,本文提出运用非接触式激光超声结合二次谐波技术检测混凝土材料早期力学性能退化的方法.
1 超声二次谐波法评估参数
当输入频率为ω 的单频超声信号时,利用材料非线性行为诱导产生二次谐波响应,如图1 所示.定义相对非线性系数β′如式(1)所示,作为混凝土早期损伤的超声检测指标[8].

图1 超声二次谐波法原理示意图Fig.1 Diagram of ultrasonic second harmonic method

式中:A2为接收信号频谱中的二次谐波幅值;A1为基波幅值;x 为超声波传播的距离.
2 激光超声二次谐波法混凝土早期损伤检测数值研究
2.1 非线性细观混凝土有限元模型
因混凝土材料本身存在的非均质以及非线性弹性特性,导致其在应力波扰动作用下表现出较强的非线性,材料的非线性力学行为也会产生二次谐波,对剥离损伤的判断有一定的影响,因此需要充分考虑混凝土的非均质特性和非线弹性本构关系.
采用蒙特卡洛法建立尺寸为300 mm×100 mm的二维细观混凝土随机骨料模型,由粗骨料、砂浆、孔隙三相组成.骨料形状不会对混凝土的破坏机理产生影响,破坏过程往往围绕界面过渡区或是缺陷造成裂缝的产生、延伸至贯穿,因此裂纹的产生位置与最终混凝土的破坏形态受骨料位置影响较大[9].因为骨料形状对该方法的影响不是很大,所以进行有限元模拟时将骨料形状简化为圆形骨料是可行的.
依据修正的二维Fuller 级配曲线计算骨料颗粒[10],假设粗骨料粒径为5~25 mm,二维截面任一点位于直径为d0的圆形骨料内的概率P 为:

式中:Pk为骨料占混凝土总体积的百分比,取0.7;d0为骨料直径,mm;dmax为最大骨料直径,mm.
计算过程如下:将粗骨料划分为5 个计算粒径d0,每个粒径区间的代表粒径为7.5 mm、12.5 mm、17.5 mm、22.5 mm.按照式(2)可得到计算粒径d0的出现概率(见表1),将粒径区间概率作为代表粒径7.5 mm 的出现概率,因此7.5 mm 粒径粗骨料数目为0.137×300×100/44.2=92.99,取93 颗.以此类推得到4 种代表粒径的骨料数目.不同混凝土模型的孔隙率介于0.8%~4.0%,以直径1~2 mm 的圆形孔作为混凝土模型的第三相,本文以提高孔隙率模拟混凝土早期力学性能退化的程度.确定了骨料数目和孔隙率的大小,通过蒙特卡洛法随机投放骨料,生成的随机骨料模型如图2 所示.

图2 随机骨料模型Fig.2 Random aggregate model
直接划分有限元网格会使网格不规则,计算接触问题时收敛困难.因此借鉴金浏[11]提出的细观混凝土等效均质化思想,对随机骨料模型按特定尺寸进行分割,依据复合材料等效化方法将各单元的力学性质(弹性模量、泊松比等)等效为各向同性的均匀介质,最终形成细观混凝土单元内均质,而不同单元之间性质各异的非均质细观模型.等效过程如下:第一步依据Mori-Tanaka 复合材料等效化方法[12]将细观单元中的孔隙和砂浆等效成具有相同力学性质的均质砂浆;第二步将均质砂浆和骨料视作并联体,求其峰值强度和等效弹性模量;第三步通过并联模型求出细观单元的峰值强度;最后通过单元的等效弹性模量和峰值强度2 个参数,对每个单元体赋予规范GB 50010—2010 中混凝土单轴应力应变关系式(C.2.3)和(C.2.4).以12.5 mm 单元尺寸为例,被分割的192 个细观单元的受拉和受压应力-应变曲线如图3 所示.
经典统计强度理论认为材料的强度性能服从Weibull 分布,在脆性材料中该分布已被证明具有较高的精度[12-13].本文假定细观单元均质化弹性模量的统计特性服从双参数Weibull 分布,统计分析细观单元的有效分割尺度.

式中:a 为尺度参数;b 为形状参数;x 为统计变量,即各单元的等效弹性模量,GPa.

图3 12.5 mm 细观单元应力-应变曲线Fig.3 12.5 mm micro element stress-strain curve
以1.8%孔隙率随机骨料模型为例,采用最大似然估计法拟合不同单元尺寸下等效弹性模量的Weibull 分布函数,以及区间估计概率分布函数95%置信度的上下限.为了找到等效细观混凝土模型力学性质满足Weibull 分布的最小单元分割尺寸,利用K-S 假设检验法对拟合的概率分布函数进行分析筛选.不同单元尺寸等效弹性模量的参数估计与假设检验结果见表2.
图4 绘制了不同尺寸单元下等效弹性模量拟合的概率密度分布函数.图中清晰地显示,单元尺寸越小,对应的形状参数b 值越小,概率密度函数图像越扁平,弹性模量分布越分散,代表材料的非均匀程度越高;单元尺寸越大,对应的形状参数b 值越大,概率密度函数图像高而窄,代表材料内部越均匀,弹性模量分布越集中.
由于混凝土材料的力学性质统计特性服从形状参数b(也称均质度)介于7~12 之间的Weibull 分布规律,因此结合表2 和图4 确定了等效弹性模量分布满足95%保证率的Weibull 分布最佳细观单元剖分尺寸为12.5 mm,其形状参数b=7.151 能够符合混凝土材料力学性质统计特性的均质度范围.
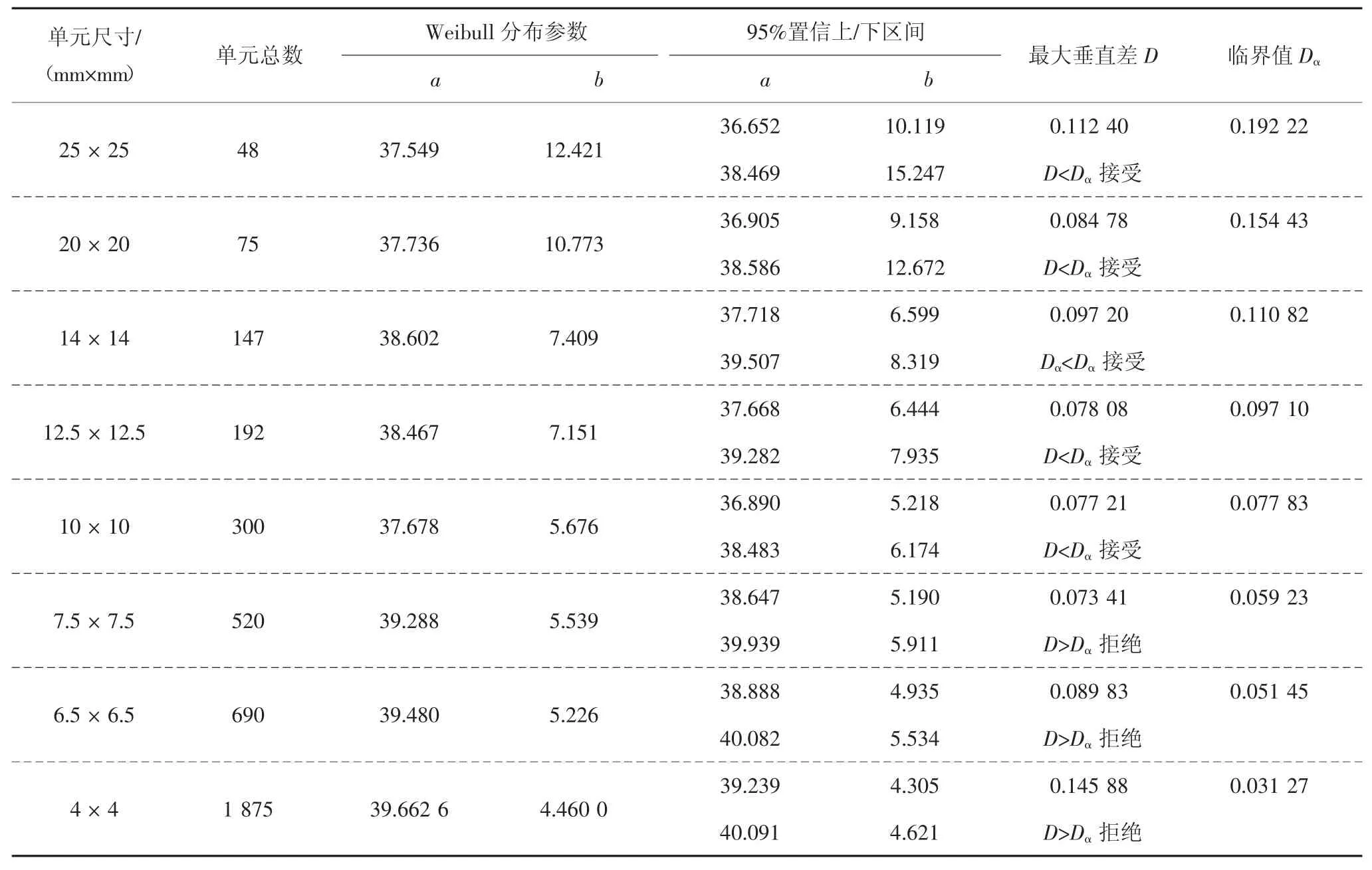
表2 不同单元尺寸下等效弹性模量的参数估计与假设检验结果Tab.2 Parameter estimation and hypothesis test results of equivalent modulus of elasticity for different element sizes

图4 等效弹性模量拟合的Weibull 分布概率密度函数Fig.4 Probability density function of Weibull distribution fitted by equivalent elastic modulus
通过孔隙率大小模拟混凝土不同程度的早期损伤状态,并观察骨料分布对参数估计的影响,建立了3 个孔隙率为1.8%不同空间分布随机骨料模型,将混凝土模型分割成12.5 mm 的单元,计算各单元的等效弹性模量等力学性质,并对其分布进行参数估计和K-S 检验,结果见表3.可以看出不同孔隙率细观模型在12.5 mm 单元尺寸下,均能服从Weibull 分布,证明选择12.5 mm 单元尺寸具有合理性;1.8%孔隙率的3 个初步损伤模型的参数估计结果基本接近,说明细观模型等效方法基本不受随机骨料空间位置分布的影响,在同一单元尺寸下计算的细观单元等效弹性模量分布具备稳定性.
图5 绘制了表3 中拟合的Weibull 分布概率密度函数图像,图中1.8%孔隙率模型对应的3 条概率函数图像近乎重叠,说明了细观单元等效方法对随机骨料的空间分布并不敏感,其稳定性很好;表中的孔隙率大小由小到大变化时(损伤程度加剧),形状参数b 从7.781 减小至6.469,图6 拟合的概率密度函数图形更加扁平,样本均值向左偏移,由38 GPa减小至35.5 GPa,因此可以得知随着损伤的发展会削弱混凝土的力学特性,同时导致混凝土内部结构力学性质不均匀性增强,这为后续研究细观混凝土模型损伤后的材料非线性特征提供了思路.
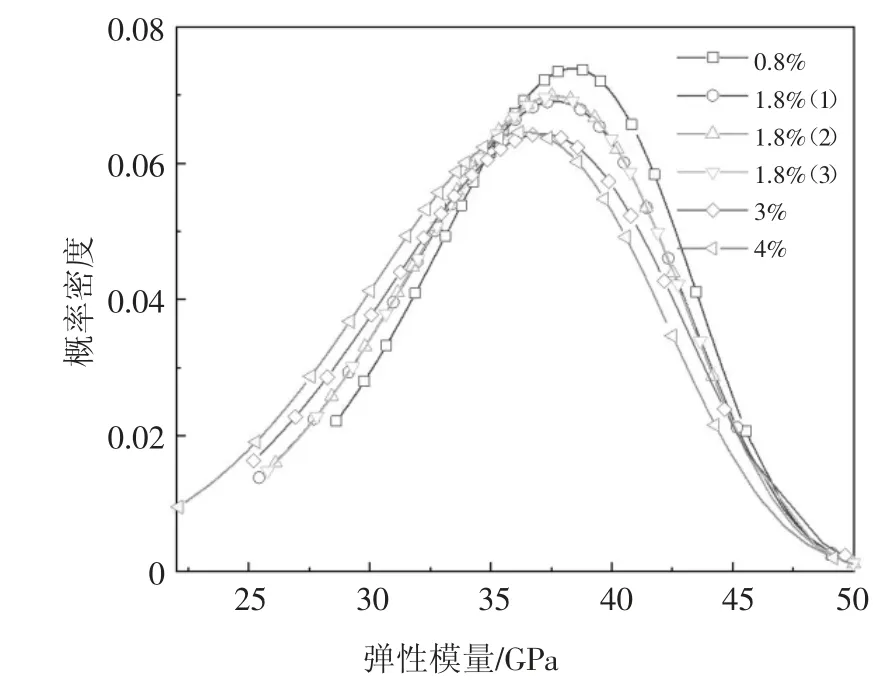
图5 不同孔隙率下等效弹性模量拟合概率密度函数Fig.5 Probability density function of fitted by equivalent elastic modulus under different porosity
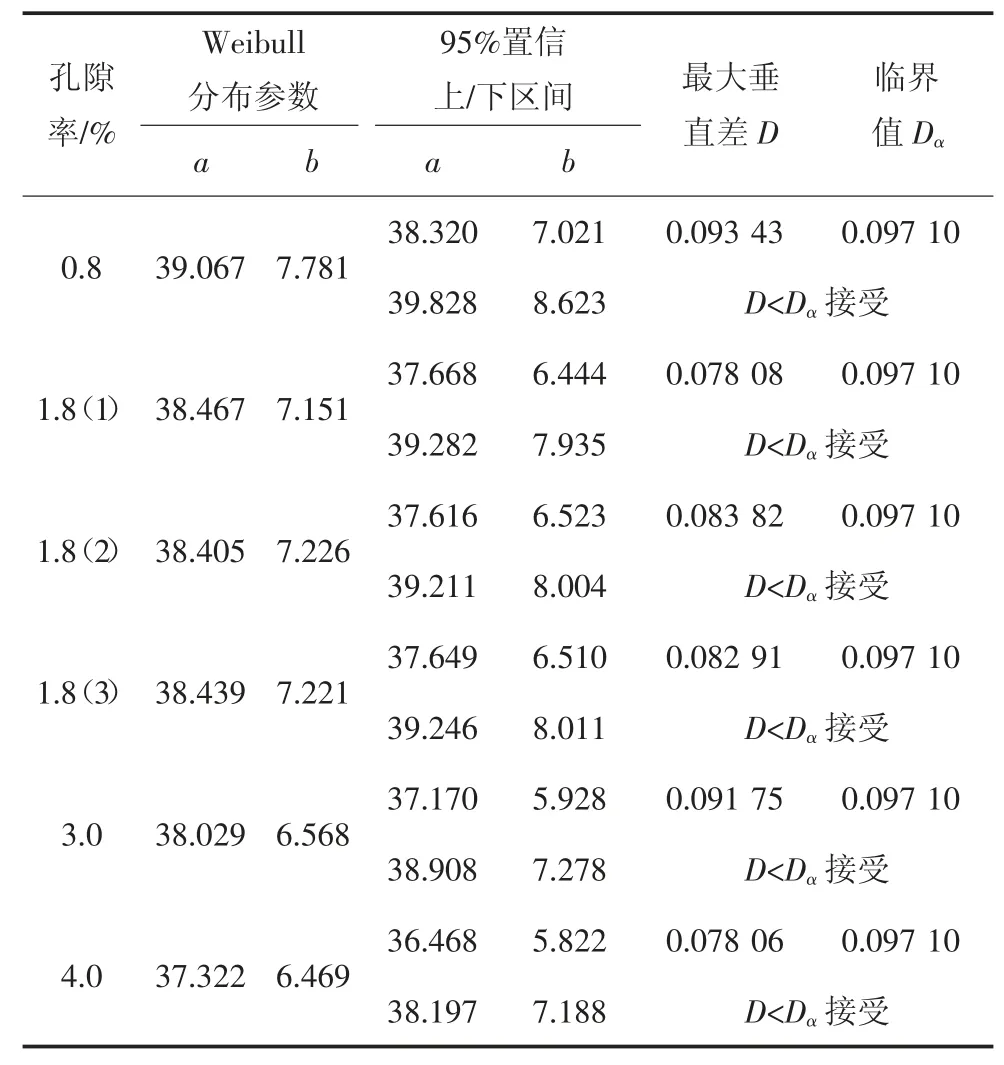
表3 不同孔隙率模型的参数估计与假设检验结果Tab.3 Parameter estimation and hypothesis test results of different porosity meso models
建立随机骨料模型、细观单元等效化、等效力学性质的统计分析、采用通过假设检验的等效弹性模量和峰值强度构造单元的非线性本构关系,上述四个步骤即为混凝土非线性细观模型的建模全过程.
2.2 激光超声有限元模型参数
本文采用COMSOL Multiphysics 软件建立激光超声模型与非线性细观混凝土模型,模拟激光超声波与非线性混凝土相互作用产生的接触非线性二次谐波响应.采用频率为50 kHz 的正弦调制激光作为激发源.由于激光器发射的激光光斑的热功率密度截面分布通常是高斯分布,在时间轴上被调制为正弦函数形式,如图6 所示.
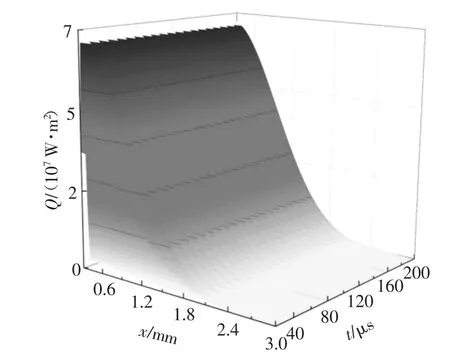
图6 功率70 W 频率50 kHz 激光激励函数Fig.6 Laser excitation function of power 70 W frequency 50 kHz
利用COMSOL Multiphysics 有限元软件建立如图7 所示的尺寸为300 mm×100 mm 的混凝土二维平面应变模型.采用笛卡儿坐标系[13],左下角为坐标原点模型等效细观单元分割尺寸为12.5 mm,设置激光功率为70 W、调制频率为50 kHz、激光加载时间为20 周,激光作用在图7 中深色矩形单元体的上边界,在激光作用浅表面区域设置网格尺寸20 μm,在非激光作用区域设置单元尺寸为1 mm,以捕捉高频超声信号.
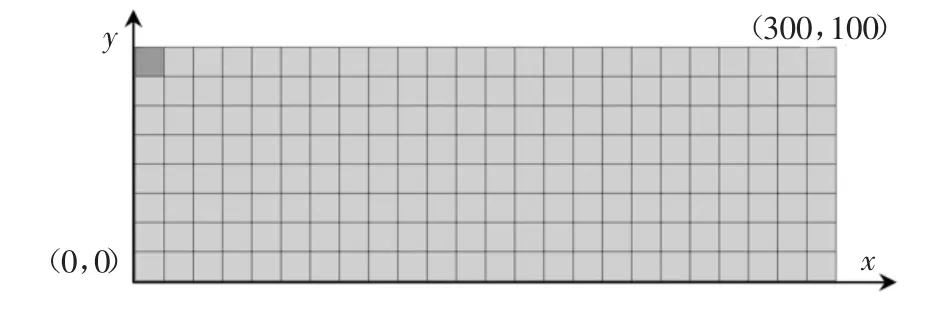
图7 二维非线性细观混凝土模型Fig.7 Two-dimensional nonlinear meso concrete model
该模型通过孔隙率大小模拟混凝土不同程度的早期损伤状态.对每个12.5 mm2单元体依次赋予2.1节所求的等效力学参数对应的混凝土单轴应力应变关系、泊松比及密度,混凝土热物理属性热扩散系数k=1.8 W/(K·m),比热容C=900 J/(K·kg).边界条件设置如下:模型上表面为自由边界,为减少反射干扰,混凝土左边界设置为对称边界,右边界和下边界为低反射边界.在模型中添加瞬态研究,计算步长取0.4 μs,总计算时长为800 μs.
2.3 激光作用下模型温度与位移结果分析
强度调制激光作用于混凝土上表面时,由于热膨胀效应混凝土将产生窄带超声表面波,经过软件的后处理得到激光功率为110 W、175.6 μs 时刻的速度云图(如图8 所示).模型中的箭头方向代表该点的速度方向,箭头的长度代表该点速度值的大小.从速度云图中可看出随着x 轴坐标正向传播距离的增加,箭头长度没有明显变化,即波动的幅值没有明显衰减;随着深度的增加,箭头长度逐渐变短,说明质点的运动符合Rayleigh 波沿表面和深度方向传播的衰减特征.
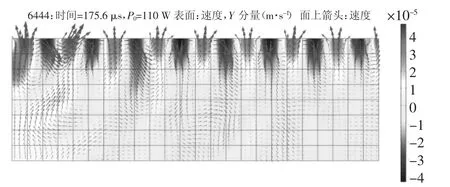
图8 175.6 μs 时刻y 向速度分量云图Fig.8 Cloud diagram of y-direction velocity component at 175.6 μs
选取功率70 W、调制频率50 kHz、加载时长20周等激光参数,在14 个不同孔隙率细观混凝土模型中激发超声表面波.如图7 所示,激光激励中心位于混凝土模型坐标(0,100).于混凝土上表面坐标点(10,100)至(300,100)之间每间隔5 mm 设置一个接收点,输出该点的y 向位移时程信号.对接收点的位移信号进行频谱分析处理,信号经汉宁窗调制后作快速傅里叶变换,利用MATLAB 编译语言自动提取基波和谐波的幅值.当激光加载在非线弹性模型时,距离激光激励100 mm 处的接收点信号时频域图如图9 所示.可以看出当激光激发的超声经过非线弹性介质时滋生了明显的100 kHz 的二阶谐波甚至150 kHz 的三阶谐波.说明在超声波微小扰动作用下,介质的超声非线性特征与材料本身的非线性应力-应变本构关系直接相关.利用产生的二次谐波响应计算混凝土材料非线性系数,即将基波幅值、二次谐波幅值及超声波传播距离代入式(1).
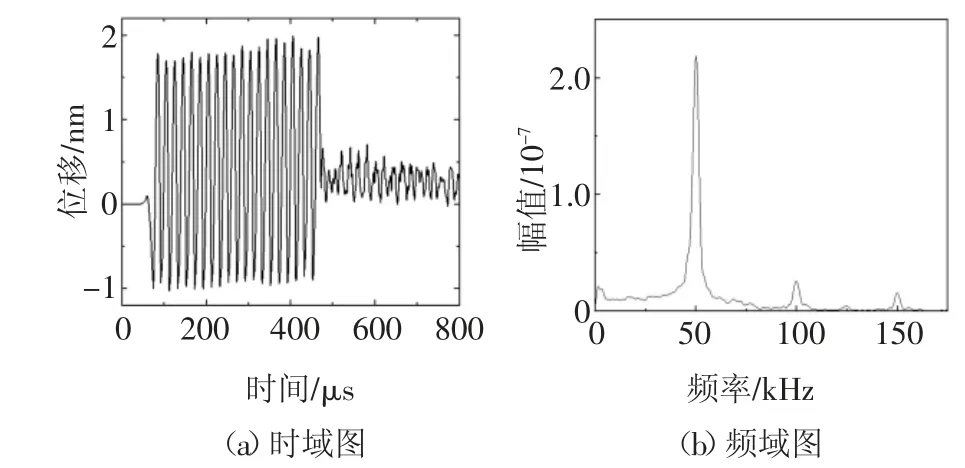
图9 非线弹性模型中接收点(100,100)处的时域和频域图Fig.9 Time-domain and frequency-domain diagrams at the receiving point(100,100)in an inlinear elastic model
从图10 可看出,相对非线性系数空间分布特征表现为在激光激发的超声波在传播10~100 mm 的距离内,相对非线性系数由大到小变化,在100~250 mm 趋于稳定.因此取100~250 mm 稳定段范围内相对非线性系数的平均值用于评估混凝土的早期损伤发展程度.
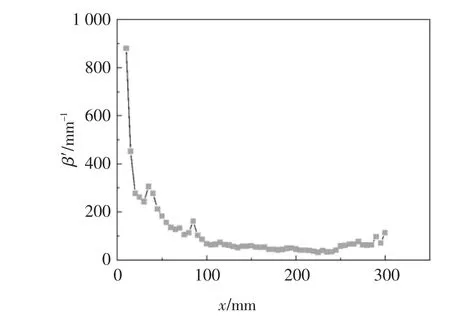
图10 接收点的相对非线性系数Fig.10 The relative nonlinear coefficient of the receiving point
2.4 混凝土材料非线性与静弹性模量
为建立混凝土材料非线性系数与宏观力学性能的关系,还需要计算混凝土细观等效模型的弹性模量,通过单轴压缩模拟获得混凝土模型的割线弹性模量[13].模型的左边界设置法向位移约束,左边界中点设置切向位移约束,在右边界分别施加法向位移荷载u1和u2,计算弹性状态下混凝土平均应力与应变的比值.有限元模型重新选择自由四边形单元网格类型,网格大小为2 mm.依据式(4)计算混凝土模型的静弹性模量.

式中:σ1,2为荷载u1,2下左边界水平方向的平均应力,MPa;ε1,2为荷载u1,2下的平均应变.
图11 表示14 种孔隙率非线性细观混凝土模型的相对非线性系数β′与静弹性模量E 的关系,并拟合得到两者之间的指数关系.可看出β′与E 呈现递减趋势,这是由于孔隙的存在会削弱单元体等效的弹性模量、峰值强度等力学特性,使得模型整体的弹性模量降低.数据点沿着连线孔隙率逐渐增大,模型的弹性模量E 从37.149 GPa 下降到35.998 GPa,下降率仅为3.1%,而对应材料的β′增长了24.82 倍.说明随着混凝土力学性质的退化,非线性力学行为增强,超声非线性响应十分显著.

图11 相对非线性系数与弹性模量的关系Fig.11 The relationship between relative nonlinear coefficient and elastic modulus
其主要原因是,混凝土内部结构越密实,材料的弹性模量越高,材料的力学行为越接近线弹性,在微小扰动作用下的超声非线性特征不明显;相反地,材料内部的初始缺陷越多,材料的弹性模量越低,则混凝土材料本构关系的泰勒展开式σ=Eε(1+βε2+o(ε3))中应变高阶项不可忽略[13].当超声波穿过非线性材料时波形产生了明显的畸变,使得非线性二次谐波效应增强,非线性系数增大,说明非线性超声二次谐波响应反映了材料的非线性,验证了材料非线性力学特性诱发超声非线性响应的本质,以及细观混凝土的材料非线性作为早期损伤材料特征评价指标的可行性.
3 压电超声检测混凝土早期损伤试验分析
3.1 试验试件
依据普通混凝土配合比设计规范和试验要求,试件龄期为28 d,混凝土配合比见表4.
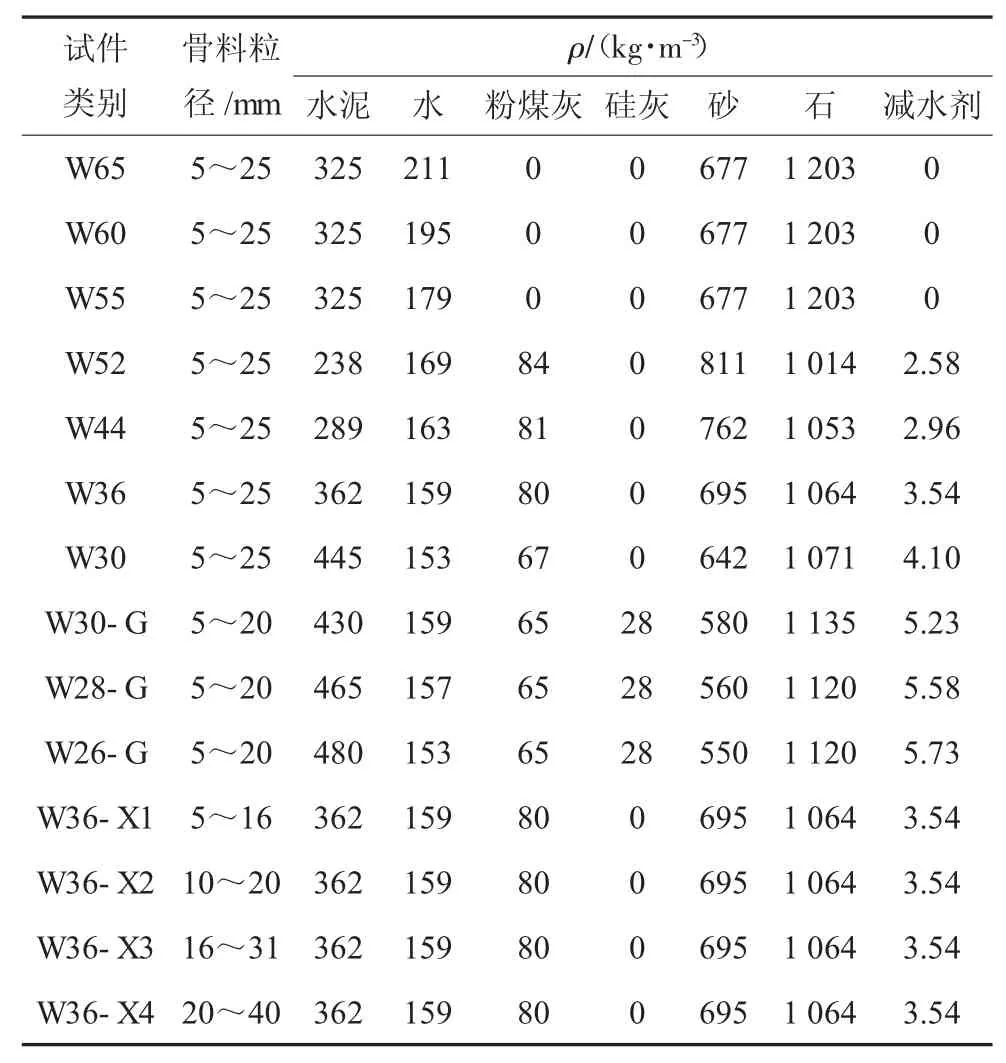
表4 混凝土配合比Tab.4 Mix proportion of concrete
试验研究不同早期损伤状态下混凝土的非线性特性,对混凝土的损伤程度通过控制高温加热温度来快速引入不同程度的损伤,仪器设备及试件如图12 所示.

图12 高温试验设备与热损伤试件Fig.12 High temperature test equipment and thermal damage specimens
根据预试验结果,当加热温度升至600 ℃并恒温0.5 h 时,混凝土表面水泥浆体收缩严重伴随肉眼可见的微裂纹,因此将600 ℃作为最高目标温度,温度梯度分别设为200 ℃、400 ℃、600 ℃,控制升温速率,逐渐升高电阻炉炉内温度,间接加热混凝土试块.
3.2 试验系统设计
激光超声的基本原理是当激光源辐照在固体介质表面时,被表面迅速吸收,引起作用点的瞬时热膨胀,而受到膨胀区周围介质的约束压应力,随后在介质中形成应力波传播出去[14].由于试验条件的限制,压电超声试验将采用表面激振法通过压电换能器施加垂直激励的形式激发Rayleigh 波,等效替代激光激励源.
应力波是指应力、应变状态的变化以波的方式传播.在可变形固体介质中机械扰动表现为质点速度的变化和相应的应力、应变状态的变化.从定义上看超声波也属于应力波,应力波是更加广义的说法.因此压电超声产生的是超声振动信号,同时也是应力波信号.本文采用的调制激光所产生应力波已达到了超声波的频率段,且模拟的激光和试验用的压电传感器在试件表面产生的均为超声表面波,区别仅为激励方法的不同,但都是利用了表面波与混凝土非线性介质的相互作用所产生的谐波现象来表征混凝土早期损伤状况,因此可以用压电超声等效激光激励.
试验检测系统主要包括激励信号发射装置与信号采集装置,试验系统设计如图13(a)所示.试验设计方案为,由数字信号发生器产生1 V 高频连续正弦激励信号,经过功率放大器增益100 倍后,传输至压电超声换能器激励混凝土试件并产生表面波,并通过表面等距离粘贴的4 个压电陶瓷片接收位移信号.响应信号通过计算机进行快速傅里叶变换,自动提取基波和二次谐波的幅值并计算相对非线性系数.
另基于ASTM C215 中的横向共振频率测量方法搭建敲击共振基频检测系统,检测混凝土试件的动弹性模量[14],试验系统设计如图13(b)所示.试验方案设计如下:使用冲击力锤对混凝土试件长边侧面中线的边缘进行敲击使其产生自由振动,振动信号由试件长边侧面中线距端面5 mm 处的磁吸式加速度传感器接收,再传输至数据采集系统进行数据保存,采样频率12 kHz,采用自由触发模式,采集时长10 s.力锤应垂直下落至试件上表面的中心线处,敲击后应迅速抬起,避免力锤影响试件的自由振动.本试验采用厚度为5 cm 的海绵垫,这种柔软的边界条件将尽可能地不约束试件的自由振动,并减小外部环境噪音的影响.
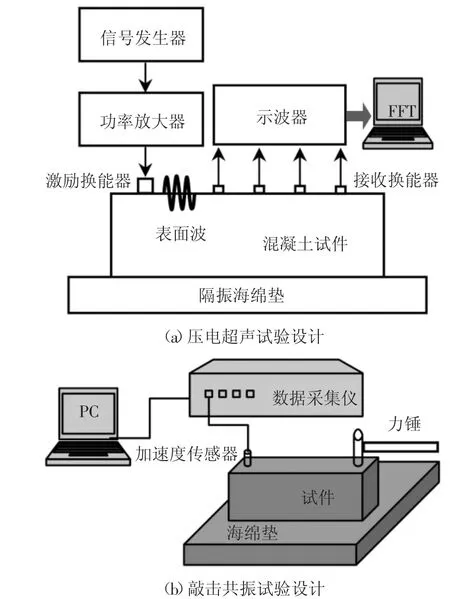
图13 试验系统设计图Fig.13 Experimental system design drawing
3.3 试验处理方法及分析
混凝土材料非线性超声检测试验在室温下进行,相对湿度保持在50%~70%.试验中,激励换能器与压电片传感器的布置图如图14(a)所示,粘贴压电片之前需在检测面上绘制定位线.检测试块W52-1时(代表水胶比0.52 的1 号试块),示波器图窗中从上至下依次代表A、B、C、D 压电片接收的信号,采集到垂直表面的位移电信号在传播过程中幅值无明显的衰减,说明压电探头表面垂直激励法在混凝土表面亦形成了稳定的表面波.

图14 压点超声试验测点布置及计算结果Fig.14 The arrangement and calculation results of pressure point ultrasonic test points
将示波器采集到的信号加汉宁窗处理及快速傅里叶变换,试件检测面上4 个采集点与激励换能器的水平距离分别为5 mm、10 mm、15 mm、20 cm,提取每个采集点信号频谱中50 kHz 和100 kHz 的幅值,通过式(1)计算相对非线性系数β′.为了减小偶然误差,对同一试件检测4 次,取4 次采集信号计算的平均值.图14(b)中绘制了10 个试件各接收点β′的空间特征.可以看出β′的空间特征与模拟结果(图10)的规律类似,当传播至一定距离后β′趋于稳定,因此取水平距离10 cm 及以后的B、C、D 三点的相对非线性系数β′平均值作为该试件的材料非线性系数.
对敲击共振试验采集到的加速度信号经过快速傅里叶变换,提取频域信号得到混凝土试块横向振动的基振频率,共振时频域信号如图15 所示.
对每个试件以均匀的力度敲3 次,取3 次横向基频振动频率的平均值计算混凝土试块的动弹性模量,敲击共振法测定混凝土试件的动弹性模量表达式见式(5).
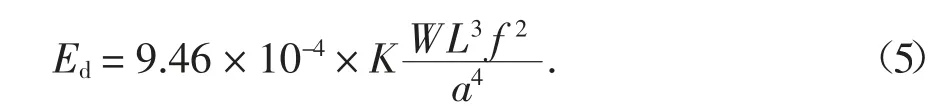
式中:W 为试件质量,当L/a=3 时取1.8 kg;L、a 分别为试件长度以及正方形截面的边长,mm.K 为试件尺寸修正系数,当L/a=3 时取1.8.f 为试件横向振动时的基频,Hz.
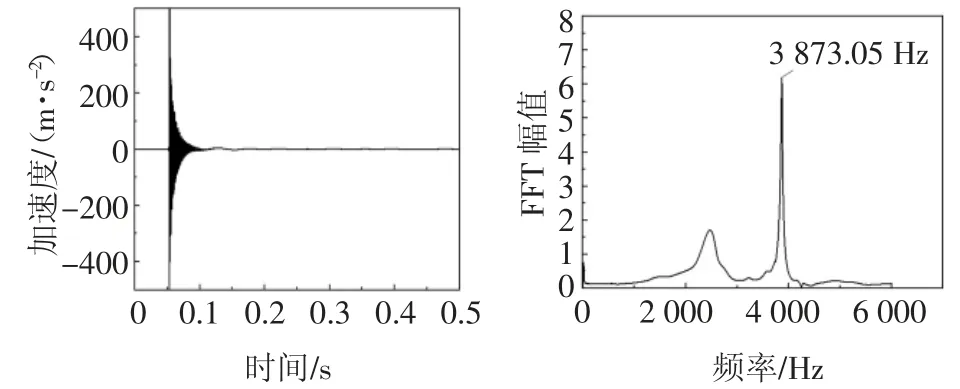
图15 敲击共振信号处理Fig.15 Signal processing of knock resonance
张健仁等[15]的动、静弹性模量试验结果,二者近似线性相关,因此动静弹性模量均可作为混凝土宏观力学性能指标.为了建立混凝土宏观力学性能与材料非线性系数的经验公式,本文将动弹性模量值Ed作为混凝土力学性能指标.
综合无热损伤与热损伤混凝土的弹性模量和超声非线性检测结果,如图16(a)所示,将横坐标β′设为以e 为底的对数坐标,图中混凝土弹性模量Ed介于40~50 GPa 时对应的β′分布在[0.1,2.7],β′的增长率约26 倍;混凝土的Ed低于40 GPa 时β′大于2.7,β′的增长率约7.95 倍.其原因是随着混凝土内部损伤加剧、裂纹的扩展导致了宏观力学参数弹性模量的降低,使得材料的非线性力学行为增强,引起超声波产生更加明显的非线性高次谐波响应,表现为相对非线性系数β′值的增大.上述表明了二次谐波法的相对非线性系数β′能够作为材料损伤特征的评价指标.通过最小二乘法拟合的指数回归方程,相对非线性系数与弹性模量相关系数为0.746 3,该指数方程包含不同强度配合比的混凝土,因此具有较强的适应性和工程指导意义.
通过图16 会发现试验结果中数据点较分散.进一步分析,产生这种现象的原因是混凝土本身的离散性比较大,试验不是理想的非接触试验以及试验过程中也会存在一些干扰因素,因此导致试验结果比模拟结果(图16(b)与图11)的离散性大.
对比线性坐标下试验结果与细观混凝土模型结果(图16(b)与图11),仿真的弹性模量仅从37.149 GPa 降低至35.998 GPa,主要原因是混凝土模型只通过增大孔隙率模拟损伤,没有考虑到试验中热损伤后的混凝土试块体积膨胀以及质量损失等状况.
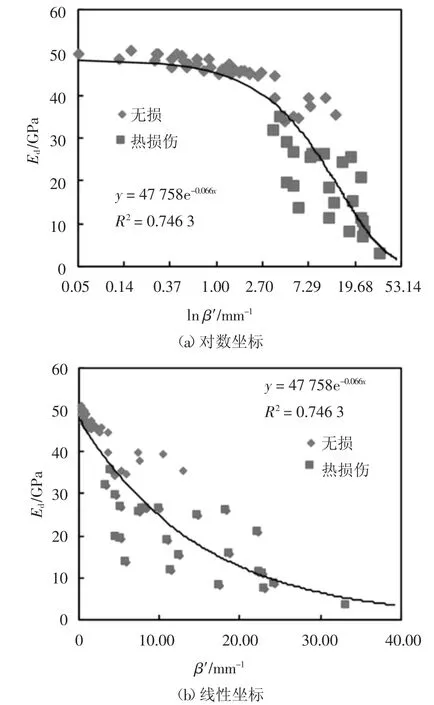
图16 混凝土早期损伤非线性超声检测结果Fig.16 Nonlinear ultrasonic testing results of concrete early damage
4 结论
1)提出了一种基于强度调制激光超声二次谐波技术的混凝土早期损伤检测方法.
2)提出了激发窄带超声波的热弹性强度调制激光技术,依据激光激励中心最高温度值不超过混凝土熔蚀阈值,选取了功率70 W、调制频率50 kHz、20周正弦调制激光激发窄带单频超声表面波信号.在强度调制激光超声作用在细观混凝土非线性模型时产生了二次谐波成分.参数分析说明随着混凝土力学性质的退化,非线性力学行为增强,使得微扰作用下应变高阶项诱导的超声非线性响应更加显著.
3)搭建了压电式超声二次谐波试验系统和敲击共振基频检测系统,建立了多种配合比混凝土材料非线性系数β′与混凝土动弹性模量Ed的指数回归方程.当混凝土的Ed介于40~50 GPa 时β′的增长率约为26 倍,当Ed小于40 GPa 时β′的增长率约为7.95 倍.试验结果验证了混凝土材料非线性作为早期损伤评价指标的可行性和优越性.

