考虑楼板作用的RC 框架压膜机制抗倒塌承载力分析
黄远,洪露露,易伟建
(1.工程结构损伤诊断湖南省重点实验室(湖南大学),湖南 长沙 410082;2.湖南大学 土木工程学院,湖南 长沙 410082)
自英国的Ronan Point 公寓倒塌事件以来,建筑结构的抗连续倒塌性能引起了广泛关注.国内外学者对纯框架结构抗连续倒塌中的受力机制[1-2]、性能评估[3-4]、动态效应影响[5-6]等进行了深入研究.在实际工程中,楼板作为框架结构的水平构件,对结构的抗倒塌承载力的贡献不可忽视.初明近等[7]进行了单向梁板子结构中柱移除的试验,研究梁板相互作用与荷载传力机制,表明楼板能够提高结构抗倒塌承载力.Pham 等采用12 点加载方式开展了一系列梁板子结构在均布荷载下的倒塌试验,研究了拆柱后的破坏模式及荷载传力路径[8].分析发现负弯矩区的T形梁作用能够明显提高结构承载力.Qian 等[9-10]进行了2 个双向梁板子结构抗连续倒塌试验并进行理论分析,以量化各种机制的贡献.杜轲等[11]设计了2 个1/3 缩尺的2×2 跨的单层框架子结构试件,进行移除中柱的连续倒塌试验,研究了考虑梁板柱协同作用的三维空间框架中,楼板对结构连续倒塌破坏形式、承载力等的影响.此外,一些学者提出了带板框架结构抗连续倒塌承载力的理论分析模型[12-14],以快速评估结构的抗倒塌承载力.
已有的研究大都关注结构连续倒塌过程中楼板受力机理的定性分析,缺乏楼板对结构连续倒塌承载力贡献的定量研究.为了准确合理地进行结构防连续倒塌设计,需要定量地分析楼板对结构抗连续倒塌承载力的贡献,并对已有规范方法的适用性进行评估和深入研究,为工程设计提供理论指导.
本文采用有限元分析软件SAP2000 建立了考虑楼板作用的框架结构抗连续倒塌分析模型,并根据相关梁柱子结构和梁板子结构连续倒塌试验对分析模型进行验证,在验证模型正确性的基础上,定义了考虑楼板作用的抗连续倒塌承载力提高系数,研究了楼板厚度、楼板宽度和配筋率等对抗连续倒塌承载力提高系数的影响,为工程设计提供参考.
1 模型建立与验证
1.1 模型建立
1.1.1 单元类型
框架梁和柱采用框架单元进行模拟.梁柱截面及配筋通过截面设计器输入,在框架单元轴线方向设置纤维铰来模拟梁柱的非线性性能,根据Mendis的建议[15],塑性铰长度设为梁高的1/2.在分析工况中几何非线性参数选择“P-Δ 和大位移”以考虑倒塌过程中的几何非线性.
楼板采用分层壳单元模拟.沿楼板厚度方向将壳单元分为12 层,分别给每一层设置相应的材料属性和厚度,如图1(c)所示.其能够耦合面内弯曲-面内剪切-面外弯曲间的相互作用,实现楼板的非线性模拟.根据面积等效原则,将钢筋层的厚度取为钢筋面积除以钢筋间距,设置钢筋层材料角模拟楼板中双层双向的钢筋网.
为了保证梁板协同作用,需将梁板上表面设为平齐,框架单元模拟梁时以顶部中点为参考点,分层壳单元以板顶面为参考面.SAP2000 中的拼接约束可使几个节点形成一个刚体,刚体约束中的节点组只能一同发生刚体运动.在拼接约束中设置距离容差,容差值范围内的节点可根据设定的自由度形成刚体约束.将每个刚体约束所包含节点的3 个位移自由度与3 个转角自由度约束住,根据分析模型单元之间的节点距离,将容差值设为260 mm.将拼接约束指定给框架单元节点与分层壳节点,保证梁和楼板连接处位移与转角的连续性,如图1(d)所示.此种建模方式能够考虑梁板的协同作用,符合结构实际受力.

图1 有限元模型Fig.1 Finite element model
1.1.2 材料本构
混凝土受压应力应变关系选用Mander 模型,其考虑箍筋对核心区混凝土的约束作用,应力应变关系如图2(a)所示.
钢筋本构选用考虑屈服平台和线性强化的弹塑性模型.在钢筋达到屈服强度前,直线斜率为钢筋弹性模量,材料的应力应变关系曲线如图2(b)所示.

图2 材料本构关系Fig.2 Stress-strain relationship of materials
1.1.3 加载方式与边界条件
在失效柱的位置处设置竖向约束,施加竖向位移荷载,直至达到目标位移值.将梁端或柱底的6 个节点自由度均约束住以模拟试验的固支条件.
1.2 模型验证
Ren 等[16]对8 个单向梁板子结构进行了中柱移除试验,其中B3 试件为无楼板的梁柱子结构对照试件,S3 试件考虑了楼板的作用.利用上述建模方式对该试件进行有限元分析,试验与模拟的荷载位移曲线结果对比如图3(a)(b)所示.B3 试件随着位移增大,远离移柱端的梁端顶部钢筋与靠近移柱端的梁端底部钢筋先后受拉断裂,钢筋断裂的顺序及位置与试验相同.S3 试件在位移431 mm 时也因靠近拆柱端的梁受拉钢筋断裂而承载力突然下降,断裂钢筋位置与试验相同.可见,该建模方式能很好地模拟二维梁柱子结构及单向梁板子结构抗倒塌性能.
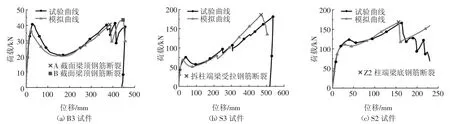
图3 试验与模拟荷载-位移曲线Fig.3 Tested and simulated load-displacement curves
钱凯等[10]进行了一系列1/3 缩尺连续倒塌试验,其中S 系列是带楼板的空间框架.利用其中的S2 试件验证本文建模方式的正确性,得到模拟和试验的荷载位移曲线见图3(c).在位移为156 mm 时,靠近拆柱端的梁底钢筋断裂,承载力下降,与试验的断裂钢筋位置相同.此外,为了进一步说明模型的合理性,本文还验证了另外9 个试件,共12 个试件.表1给出了试件的试验结果与模拟结果对比.可看出,有限元模型所得结果与试验结果拟合得较好.说明本文建模方式合理,计算结果准确可靠.
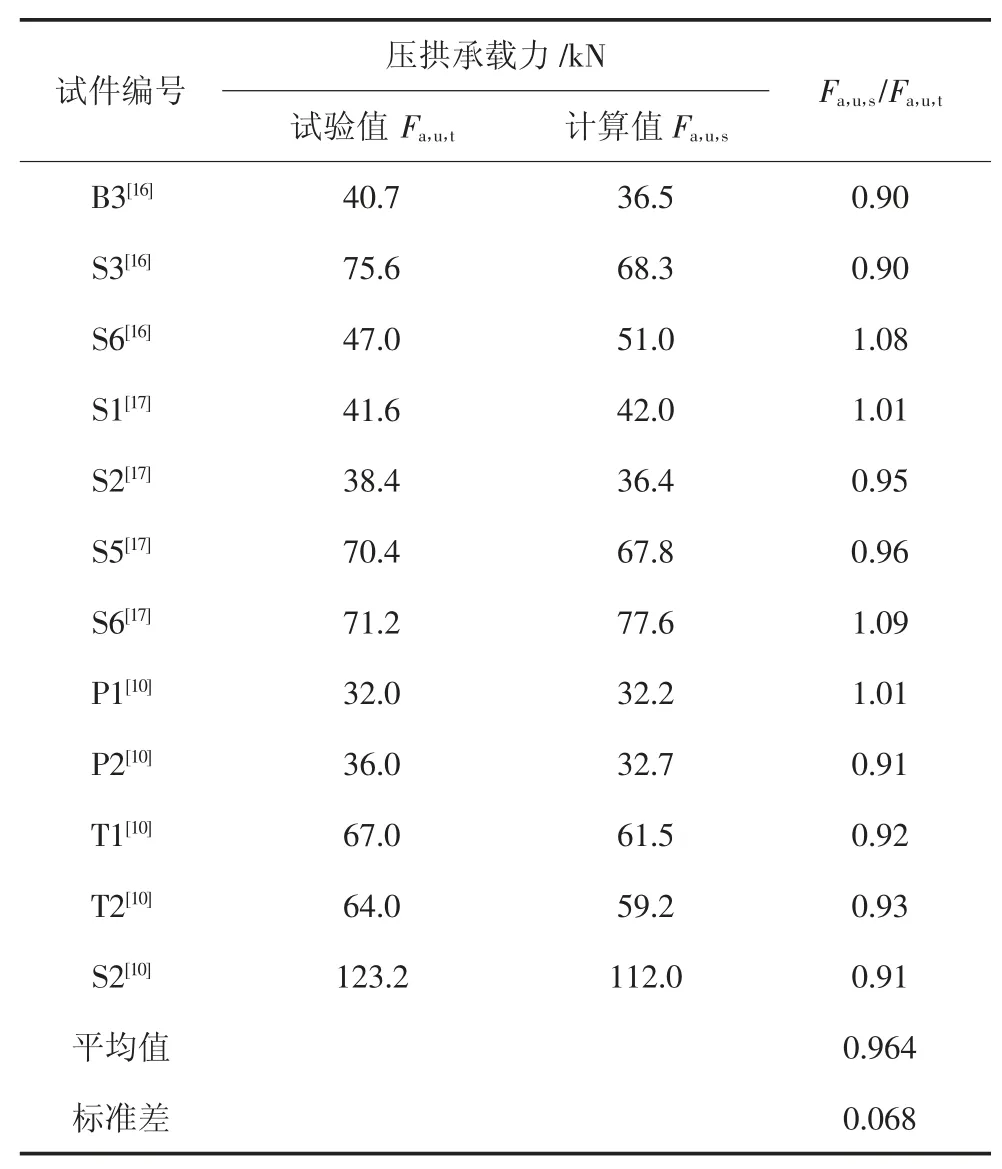
表1 试验与模拟结果对比Tab.1 Verification of test and simulation results
2 RC 框架结构的设计
已有的RC 框架连续倒塌试验试件大都为缩尺结构模型,并且未按照我国规范进行设计,因此难以反映我国的工程实际.为了研究实际的足尺RC 框架抗连续倒塌性能,本文采用PKPM 设计一幢满足我国规范要求的6 层钢筋混凝土框架结构,进行足尺模型的有限元分析.X、Y 向跨度为6 000 mm,底层层高4 200 mm,其他层层高3 600 mm.整体模型几何尺寸如图4 所示.
楼面、屋面恒荷载均为5 kN/m2,活荷载为2 kN/m2.场地类别为Ⅱ类,抗震设防烈度为6 度,设防地震分组为第一组.梁、柱受力纵筋选用HRB400,梁柱箍筋及楼板钢筋选用HRB335.混凝土等级为C30.楼板厚度为120 mm,板底配筋为8@180 mm.选取第一层梁板子结构作为基准模型进行中柱移除分析,如图4(b)阴影部分所示.梁、板详细配筋如图5所示.

图4 原型结构布局Fig.4 Prototype structure layout
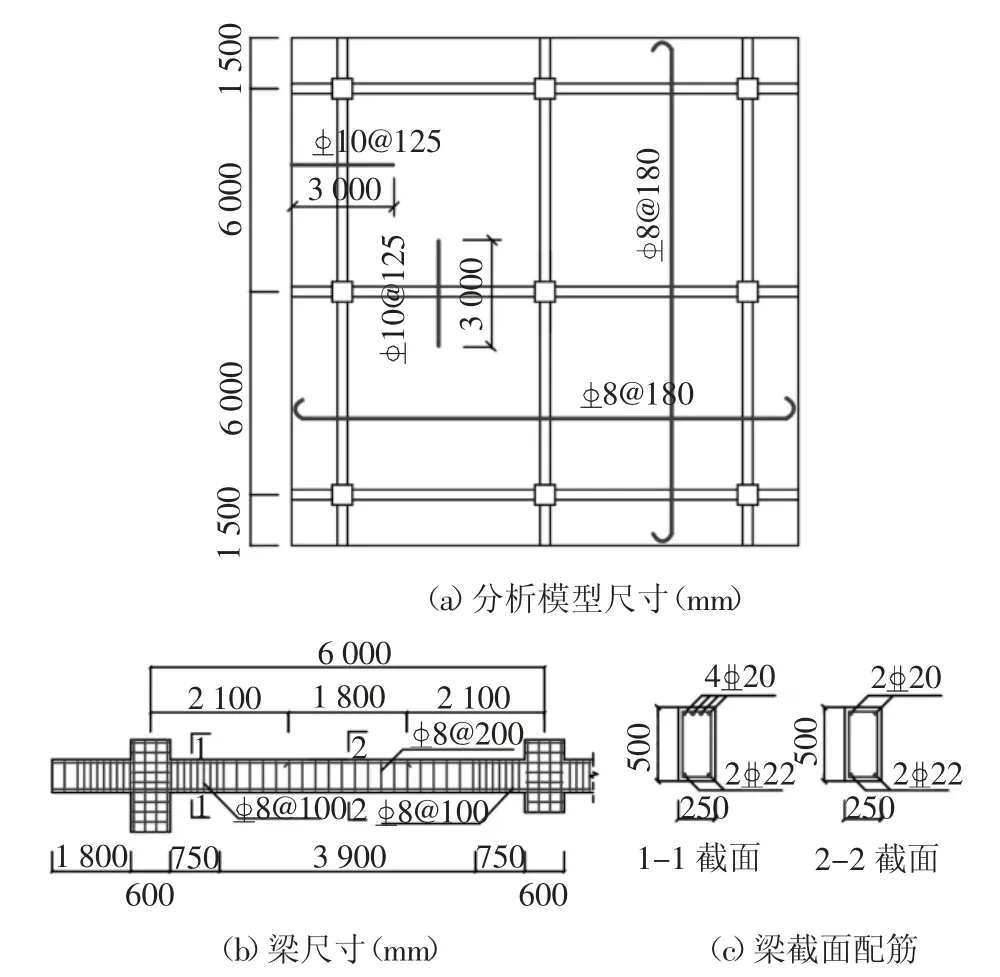
图5 分析模型几何尺寸与配筋图Fig.5 Dimension and reinforcement details of analysis model
3 RC 梁板结构抗倒塌受力机制
对基准模型BS 模型进行Pushdown 分析,荷载位移曲线如图6 所示.
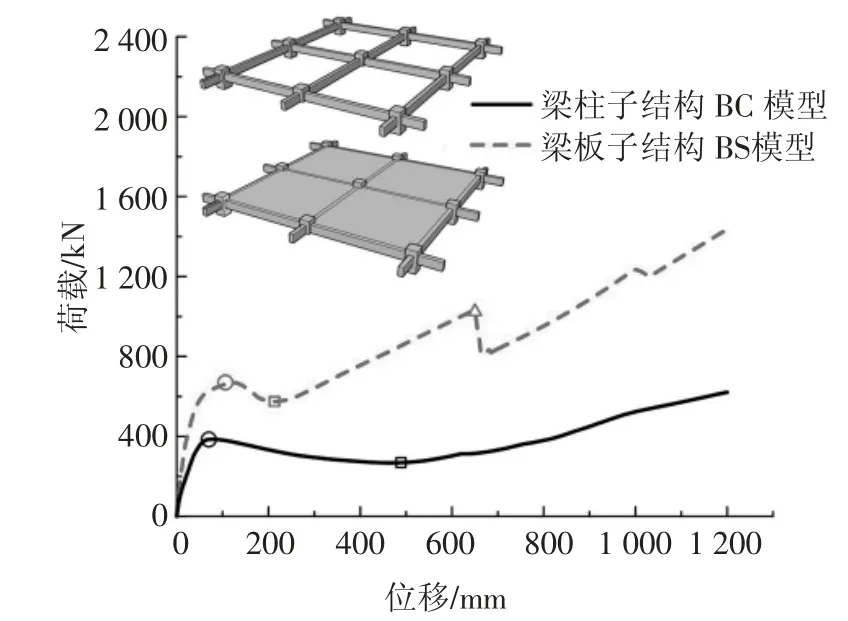
图6 BC 与BS 模型荷载-位移曲线Fig.6 Load-displacement curve of BC and BS model
在加载初期(如竖向位移为30 mm)时,楼板作为T 形梁的翼缘,中柱附近的顶层混凝土受压,边柱附近的顶层混凝土受拉,如图7(a)所示.靠近中柱的梁端顶部钢筋受压,底部钢筋受拉,表明该处为正弯矩,靠近边柱的梁端顶部钢筋受拉,底部钢筋受压,表明该处为负弯矩,如图8(a)所示.此时梁板处于受弯阶段.
随着位移逐渐增大至98 mm,承载力达到峰值点,此时梁弯矩如图9(a)所示,靠近边柱的梁端弯矩大于靠近中柱的梁端弯矩,这是因为靠近边柱的梁端轴力对截面弯矩的加强更大.此时板顶四周支座附近受负弯矩,板底出现主要沿对角线分布的正弯矩,如图10 所示.在竖向位移为211 mm 时,承载力再次上升,试件进入悬链线状态.竖向位移为220 mm 时,靠近中柱的梁端顶部和底部钢筋均受拉屈服,靠近边柱的梁端顶部钢筋受拉,底部钢筋受压,如图8(b)所示.表明靠近中柱的梁发展悬链线机制,但由于楼板作为受拉翼缘,靠近边柱的梁端处于受弯状态.此时,中柱附近楼板的顶层混凝土为拉应变,中心区域产生拉膜作用,如图7(b)所示.当位移达到300 mm 时,外围楼板会由于楼板向内移动产生挤压,形成压缩环,能够为中心区域的拉膜力提供约束,如图11 所示.
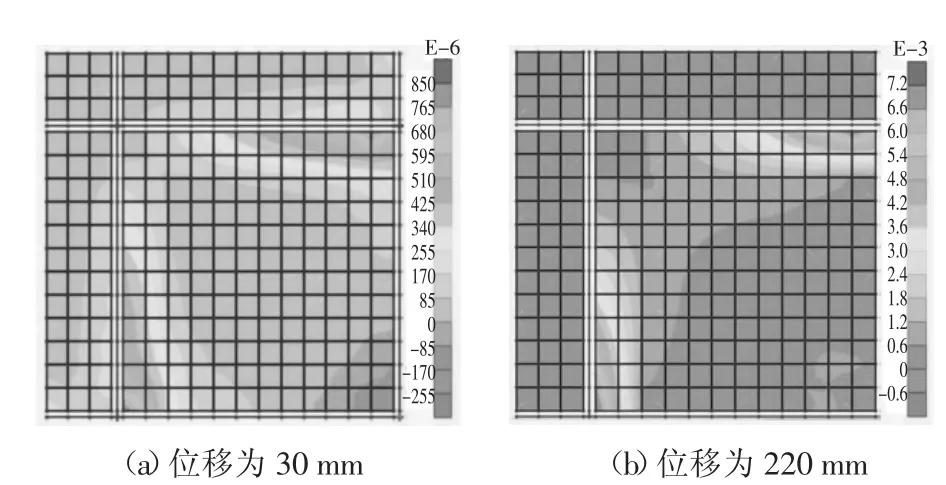
图7 分层壳顶层混凝土应变云图Fig.7 Concrete strain on top of layered shell

图8 梁钢筋应变Fig.8 Reinforcement stress of beam
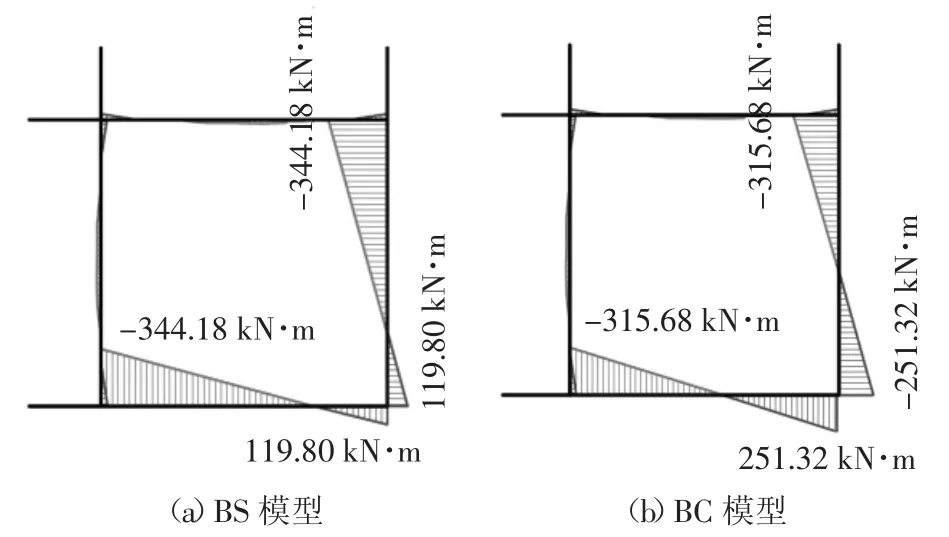
图9 BS 与BC 模型弯矩图Fig.9 Bending moment for BS and BC models
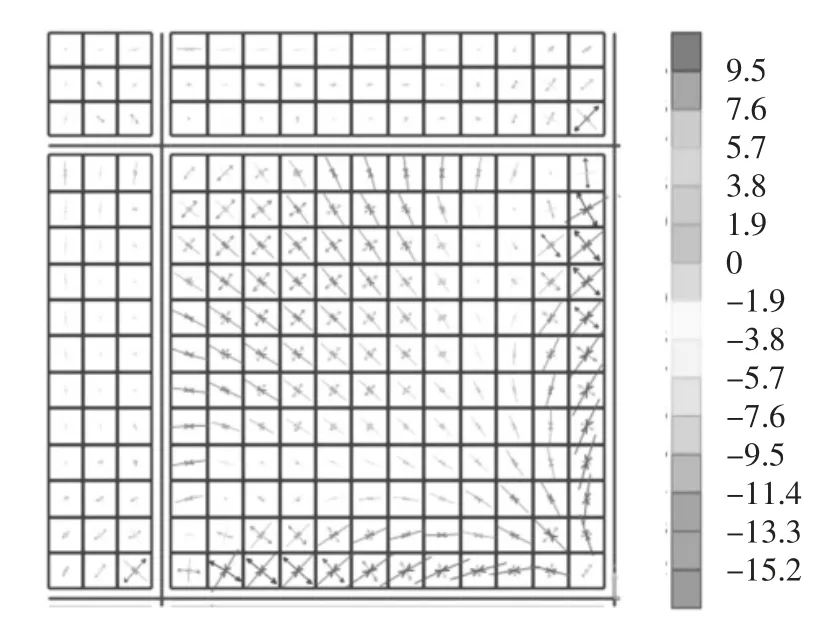
图10 分层壳单位长度弯矩图(单位:kN·m/m)Fig.10 Moment of unit length of layered shell(unit:kN·m/m)

图11 分层壳单位长度轴力图(单位:N/mm)Fig.11 Axial force of unit length of layered shell(unit:N/mm)
对不带板的梁柱子结构BC 模型进行分析,并与BS 模型分析结果进行对比,所得荷载位移曲线如图6 所示.可见,楼板提高了结构的初始刚度和承载力.BC 模型的压拱承载力为385.5 kN,BS 模型的压拱机制承载力Fa,u为674.9 kN,提高了75.1%.此外,在BS 模型中,位移为211 mm 时,承载力再次上升.在BC 模型中,位移为510 mm 时,压拱机制才转换为悬链线机制.因此楼板发展的拉膜作用使BS 模型在较小位移时,承载力得以再次上升.同时,BS 模型在643 mm 处,承载力突然下降.这是靠近拆柱端的梁底部钢筋断裂造成的.BS 模型在靠近拆柱端的梁端,由于楼板的存在,使得梁底钢筋产生更大的拉应变,因此BS 模型会先于BC 模型发生梁受拉钢筋拉断.
BC 模型达到压拱机制承载力时与BS 模型达到压拱机制承载力时,梁弯矩如图9 所示(由于双对称性,取1/4 结构说明).可见,楼板的存在使梁端负弯矩增大,提高了该截面的抗弯承载力,而梁端正弯矩减小.
以梁纵向受拉钢筋屈服作为梁形成塑性铰的标志,分析楼板的存在对梁中形成塑性铰的影响.由图12 可看出,在梁端负弯矩区内,楼板的存在推迟了梁塑性铰的形成.这是因为楼板中的受拉钢筋增大了梁混凝土受压区高度,导致受拉钢筋屈服时的截面曲率更大,所需梁端相对竖向位移增加,进而推迟了梁中塑性铰的形成,而在正弯矩区内,楼板的存在使得梁端塑性铰在更小的位移处就形成了.
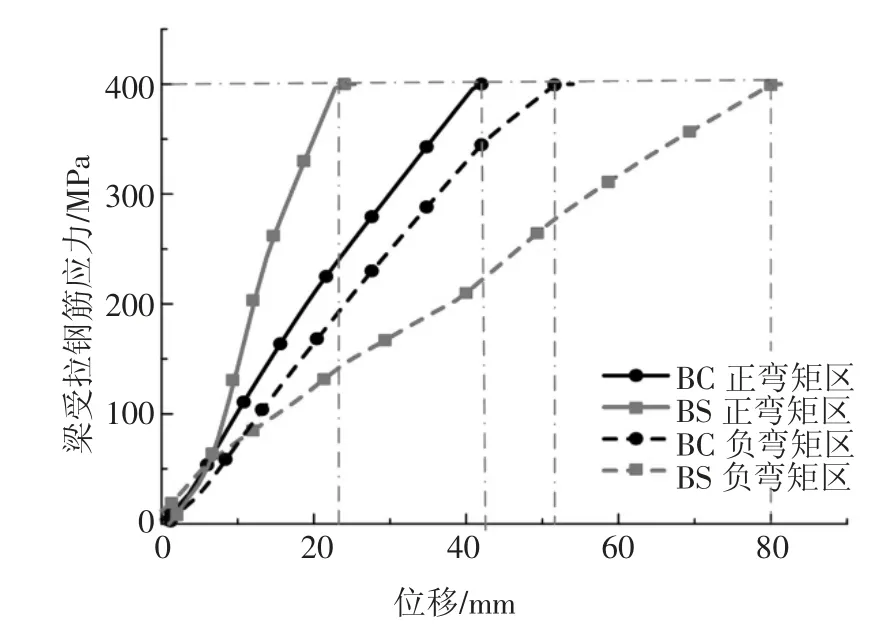
图12 梁端受拉钢筋应力-位移曲线Fig.12 Stress-displacement curve of tensile reinforcement at the beam end
靠近拆柱处的板顶钢筋应变随位移的变化如图13 所示.加载初期,靠近拆柱处的板作为梁的翼缘,在正弯矩下处于受压状态.在位移达到120 mm 后,压应变减小,楼板的压膜作用逐渐降低.在位移193 mm 后,板顶Y 向钢筋与X 向钢筋先后转变为拉应变(BS 模型中板顶Y 向钢筋位于X 向之下,故Y 向钢筋先达到受拉状态).此时楼板已处于拉膜效应状态.在拉膜作用下,梁板子结构BS 模型的承载力再次提高.
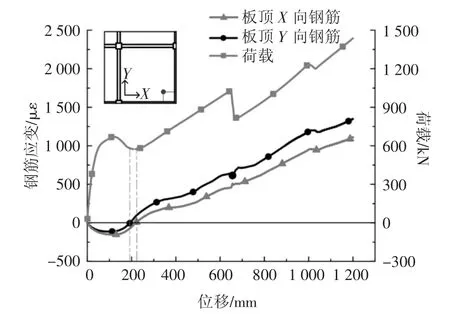
图13 BS 模型板顶钢筋应变-位移曲线Fig.13 Strain-displacement curve of top reinforcement of the slab of BS model
4 RC 梁板结构抗倒塌承载力影响因素
为了量化各参数对压拱机制承载力Fa,u的影响,定义梁板子结构压拱机制承载力的提高系数α=Fa,u/Fy,式中Fy为梁的经典塑性铰理论承载力Fby和板形成屈服线时的承载力Fsy之和.图14 为梁板结构形成塑性机制示意图,梁形成塑性机制时在端部会出现2 个塑性铰,Fby的计算[2]如式(1)所示.板在集中荷载下形成了沿周边支座的椭圆形负弯矩屈服线和沿椭圆周径向的正弯矩屈服线.根据平衡条件可以得到板的屈服线承载力[18]如式(2)所示.

图14 塑性铰与屈服线模式Fig.14 Plastic hinge and yield line mode
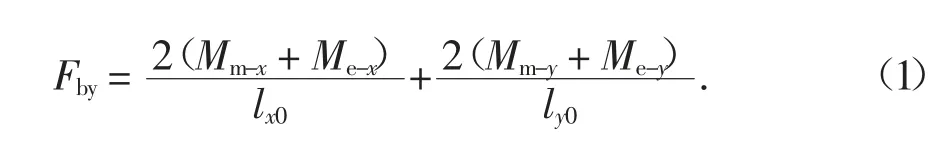
式中:Mm-x、Me-x、Mm-y、Me-y分别为x 向梁、y 向梁梁端截面正、负弯矩承载力;lx0、ly0分别为x、y 向梁净跨长.

4.1 混凝土强度等级
选取C30、C40、C50 三种强度等级混凝土进行分析,结果如图15(a)所示.压拱机制承载力和α 值均随着混凝土等级的提高而有明显提高,塑性机制承载力则保持不变,这是因为该结构双筋截面梁的混凝土受压区高度计算值x 小于,梁的抗弯承载力为M=fyAs(h0-),与混凝土强度无关,板的屈服线承载力也保持不变.但混凝土强度的提高能够显著提高梁的压拱作用与板的压膜作用,故提高系数α 值会随之提高.
4.2 楼板厚度
楼板厚度hs对承载力提高系数的影响如图15(b)所示.压拱机制承载力随着板厚的增加而增加,但α 值随着板厚的增加而减小.根据Su 等[19]的研究,跨高比越大,压拱机制对承载力的提高越小.在分析模型中,楼板的跨厚比不小于40,压膜作用较小,板厚的增加主要提高了板的抗弯承载力,对楼板压膜承载力的提高有限,而板的抗弯承载力计算值会随着板厚的增加呈线性增加,故α 值减小.
4.3 楼板配筋率
4.3.1 板顶配筋率
不同楼板顶部配筋率ρst模型的分析结果如图15(c)所示.压拱机制承载力随板顶配筋率增加而略微提高,但α 值减小.在梁端正弯矩区,楼板为T 形梁的翼缘,此时板顶钢筋为受压钢筋,因此提高板顶配筋率不能显著增大梁端正弯矩区承载力.在梁端负弯矩区,板顶钢筋为受拉钢筋,混凝土受压区高度相比于纯框架增加了52%,内力臂减小了62 mm,削弱了板顶配筋率提高对承载力的影响,因此梁端负弯矩区承载力也未显著增大.
4.3.2 板底配筋率
对不同的楼板底部配筋率ρsb的模型进行分析,结果如图15(d)所示.随着板底配筋率的增加,压拱机制承载力略微提高,但α 值减小.这是因为在梁端正弯矩区内,受压区高度由于楼板存在而变小,中性轴位于翼缘内,板底钢筋受拉且距离中性轴较近,故提高板底配筋率时,正弯矩区的承载力无明显增大.在梁端负弯矩区,板底钢筋距离中性轴仅40 mm,拉应变较小(0.000 3 左右),提高板底配筋率也未显著提高负弯矩区的承载力,但其可以线性地提高板的抗弯承载力计算值,故α 值减小.
4.4 楼板长宽比(梁跨高比)
通过调整X 向跨度来改变楼板的长宽比n,将X 向跨度改为4.5 m、3.6 m 和3 m 得到的楼板长宽比分别为1.33、1.66 和2,同时梁的跨高比由12 变为9、7.2 和6.分析结果如图15(e)所示.随着楼板长宽比提高,压拱机制承载力与α 值均增大.这是因为跨度的减小导致X 向梁的跨高比减小,梁的抗弯承载力与压拱效应产生的附加承载力均会提高,同时,楼板跨厚比减小使压膜作用也有所提高,α 值随之增加.因此,当结构承载力不足以抵抗倒塌时,可通过合理减小跨度的方式来提高抗倒塌承载力,同时使得梁、板的压拱(膜)效应得到更好的发挥.
4.5 梁配筋率
4.5.1 梁顶部配筋率
不同梁顶部配筋率ρbt的模型分析结果如图15(f)所示.随着梁顶部配筋率的提高,压拱机制承载力Fa,u仅有微小提高,而α 值有明显下降.这是因为在梁端正弯矩区,梁顶钢筋受压且压应力很小,提高梁顶配筋率时,梁端正弯矩区承载力无明显提高.同时在梁端负弯矩区,楼板作为受拉翼缘,板中钢筋的存在使受压区高度相比于纯框架增加了52%,减小了受拉钢筋到压应力合力点的距离,故提高梁顶配筋率对梁端负弯矩区承载力的影响很小(梁顶配筋率从0.82%提高到1.36%时,梁端弯矩由297.1 kN·m 增大到321.7 kN·m).提高梁顶配筋率,压拱机制承载力的提高十分有限,而梁的抗弯承载力计算值会有线性提高,因此α 值降低.
4.5.2 梁底部配筋率
不同梁底部配筋率ρbb的模型分析结果如图15(g)所示.随着梁底部配筋率的提高,压拱机制承载力Fa,u和α 值随梁底配筋率的提高而增大.在靠近中柱的梁端,提高梁底部配筋率增大了梁端轴拉力(梁底配筋率从0.66%提高到1.32%时,梁端轴拉力由295.4 kN 增大到575.1 kN),使其竖向分力提供了更高的承载力.同时在负弯矩区内,梁底钢筋均达到受压屈服,提高梁底部配筋率使得梁端轴压力增大,进而提高了梁端弯矩承载力.相比于梁顶配筋率,增大梁底配筋率对压拱机制承载力的提高更明显.因此在抗倒塌设计时,宜优先增加梁底配筋率来提高抗倒塌能力.
4.6 梁高
对不同梁高hb的模型进行分析,结果如图15(h)所示.随着梁高的增加,压拱机制承载力与提高系数α 值均提高.在周育泷等[20]的研究中,压拱机制承载力由梁端弯矩承载力和轴力带来的附加弯矩承载力组成.梁高的增加使这两部分的承载力均有所提高,而承载力计算值中梁的计算部分只能反映梁端弯矩承载力的提高,因此提高系数α 值增大.

图15 各参数的影响Fig.15 Effect of various parameters
5 经验计算公式
根据以上结果,混凝土强度等级、楼板长宽比、梁底部配筋率、梁高是影响提高系数α 值的主要因素.利用Origin 进行非线性回归分析,得到α 值的经验计算公式,如式(3)所示.公式计算所得α 值与有限元所得α 值对比见图16,达到了较好的拟合程度.

式中:fc为混凝 土强度,MPa;为C30 混凝土强度,MPa;hb为梁高,mm;为基准模型的梁高,取500 mm.
对于楼盖系统,计算塑性承载力Fy后,通过公式Fa,u=Fy即可求得压拱机制承载力,为工程设计提供参考.
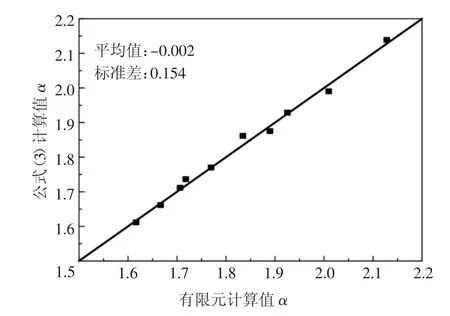
图16 有限元结果与公式结果对比Fig.16 Comparison of finite element results with formula results
6 结论
本文采用有限元软件SAP2000 对梁板子结构抗连续倒塌承载力进行了研究,在验证模型正确性的基础上,分析了混凝土强度、楼板厚度及配筋率、长宽比、梁配筋率、梁高对梁板子结构压拱机制承载力以及提高系数α 值的影响,得到如下结论:
1)楼板的存在能够显著增大钢筋混凝土框架结构的抗连续倒塌承载力,对于本文所分析的常用工程参数范围,其提高幅度在51%~101%.
2)提高混凝土强度、增大板长宽比、提高梁底配筋率以及增大梁高可有效地提高梁板子结构压拱机制承载力和提高系数α 值.
3)增加板厚,提高板顶配筋率、板底配筋率以及梁顶配筋率,对压拱机制承载力的提高不明显,且塑性承载力的提高幅度大于压拱机制承载力,提高系数α 值随着这些参数的提高反而降低.
4)提出了计算提高系数α 值的经验计算公式,可为工程设计提供参考.

