基于GD-FNN和参考模型的无人艇航向鲁棒自适应控制
包 涛,董早鹏,张 波,韦喜忠
(1.中国船舶科学研究中心,江苏无锡214082;2.高性能船舶技术教育部重点实验室(武汉理工大学),武汉430063;3.武汉理工大学交通学院,武汉430063)
0 引 言
无人水面艇(Unmanned Surface Vessel,USV),简称无人艇,是一种能够在水面上自主规划、自主导航的小型化、无人化的智能平台[1-2]。由于其具有体积小、机动性强、航速快、应用范围广等特点,无人艇近年来已成为国内外智能化海洋装备领域的研究热点和重点[3-4],而无人艇的航向控制技术是无人艇装备研制过程中的一项基本而关键的技术。
由于无人艇在水面航行时易受风浪流等环境因素干扰,同时具有复杂的非线性控制系统,因此需要较优的控制方法。进入20 世纪以后,各种智能控制技术开始蓬勃发展[5],如粒子群算法[6]、神经网络[7]和遗传算法[8]等。其中船舶的模糊控制[9]及神经网络[10]为智能控制的两大核心技术,成功解决了许多实际控制问题[11-12],但是模糊控制最大的缺点就是学习能力差、稳态精度低,而神经网络控制的最大缺点就是推理能力差、过渡过程慢。在20 世纪80 年代后期的日本,出现了一系列有关模糊神经网络的文章。自此,模糊神经网络控制由于两者之间的互补性在控制领域已经成为一个研究热点。
2001 年,Wu[13]首先提出了一种基于扩展径向基神经网络、在线自组织学习的广义动态模糊神经网络(Generalized Dynamic Fuzzy Neural Network, GD-FNN)学习算法, 算法综合了模糊控制和神经网络的优势,并通过学习在线生成和修剪模糊规则;其后Gao[14]基于GD-FNN 设计了一种用于机械手的自适应控制方法,并通过仿真实验验证了其具有良好的控制性能;陈虹丽[15]基于GD-FNN 对水翼船纵向运动受扰设计了一种估计分析方法,验证了GD-FNN 的可行性,但是并没有对算法本身进行改进;俞建成[16]基于GD-FNN 提出了一种水下机器人的直接自适应控制方法,并分析了该控制器的稳定性,用仿真实验验证了控制方法的有效性。
本文基于广义动态模糊神经网络在线学习高速无人艇的航向控制系统的逆动态模型,结合无人艇航向控制的参考模型,设计了使用参考模型的鲁棒自适应模糊神经网络控制器(Robust Adaptive Fuzzy Neural Controller with Reference Model,RAFNCRM)解决高速无人艇的航向控制问题,然后基于Lyapunov理论进行了控制器的稳定性分析,最后在有干扰的一般环境中进行了半物理仿真实验,验证了鲁棒自适应模糊神经网络控制器的有效性,提高了高速无人艇航向控制的灵活性、鲁棒性和准确性。
1 高速无人艇建模
1.1 无人艇航向操纵运动模型
随着船舶操纵控制的不断发展,对船舶控制精度的要求正在变得越来越高,相比于以前经常采用的最简形式的线性Nomoto 模型,具有非线性特征的Norbbin 模型显然能够更加精确地描述船舶的运动,从而提供精度更高的航向控制。因此采用无人艇航向非线性操纵运动模型如下:

式中:r为首摇角速率;δ 为舵角;T 为追随性时间常数;K 为舵角增益;α 为Norbbin 系数,其具体数值可以由螺旋实验确定;d为干扰;ψ为航向角。
对于式(1)所示的无人艇航向非线性操纵运动模型,可以看作如式(2)的非线性动力系统:

对比式(1)和式(2),可以将式(1)改写为

1.2 无人艇风浪流干扰模型
无人艇在航行中必然会受到环境扰动的影响,在对无人艇航向控制进行仿真时,建立合适的扰动模型是一个重要环节。作用于无人艇的环境扰动分为两类:一类是风、流扰动;另一类是海浪扰动。
在工程上,风流扰动可以用一个常值加上白噪声来模拟,其就可以较好模拟风流干扰。而海浪的随机干扰过程可以通过对海浪谱密度的描述进行概括。文献[17]中使用了一个二阶海浪模型来模拟实际的海浪干扰,如式(5),其将海浪对无人艇的运动影响等效为海浪对无人艇舵角的影响,从而模拟海浪的干扰。

2 基于GD-FNN的无人艇航向鲁棒自适应控制(RAFNCRM)
2.1 广义动态模糊神经网络结构
单独使用模糊系统控制或者神经网络控制进行结构辨识是比较耗时的一件工作,因此文献[18]提出了一种动态模糊神经网络(Dynamic Fuzzy Neural Network,D-FNN),其算法的参数调整和结构辨识同时进行,学习速度快,但其也有不少缺点,如统一规则中输入变量的所有高斯隶属函数的宽度都一样,一些隶属函数高度重叠,抽取出的模糊规则难以理解等。在文献[18]提出的D-FNN 算法基础上,文献[14]提出了一种新的算法—广义动态模糊神经网络。该算法基于椭圆基函数(Elliptic Basis Function,EBF),在功能上等价于TSK(Takagi-Sugeuo-Kang)模糊系统。提出模糊ε完备性作为在线参数分配机制,避免初始化选择的随机性,同时每条规则的输入变量的宽度可以根据它对系统贡献的大小实施在线自适应调整。
广义动态模糊神经网络的结构如图1所示。


图1 广义动态模糊神经网络结构Fig.1 Structure of GD-FNN
式中,μij是xi的第j 个隶属函数,cij和σij分别为xi的第j 个高斯隶属函数的中心和宽度。由于计算每个规则触发权的T-范数算子是乘法,图1中第三竖层的第j个规则的输出Rj( j = 1,2,…,u )可以表示为

第四竖层每个代表一个输入信号加权和的输出变量,如式(8)所示。

式中,y是一个输出变量的值,wj是结果参数或者第j个规则的连接权。
将式(8)写成矩阵形式,得

式中,W ∈Ru(r+1)为广义动态模糊神经网络输出权值矩阵,Φ ∈Ru(r+1)×n为输出层节点数,Y ∈Rn为广义动态模糊神经网络的输出向量。
2.2 鲁棒自适应模糊神经网络控制器(RAFNCRM)设计
鲁棒自适应模糊神经网络控制器(RAFNCRM)的结构图如图2所示。

图2 RAFNCRM控制器结构图Fig.2 Structure of RAFNCRM
鲁棒自适应模糊神经网络控制器(RAFNCRM)按照如下方式工作:首先控制器通过广义动态模糊神经网络学习算法(GD-FNN)构建的GD-FNN_A 模块获取无人艇控制模型的逆动态,即从zˉ到u的映射关系,广义动态模糊神经网络学习算法(GD-FNN)可以确定适当的模糊神经系统的结构参数,从而得到合适的映射关系;GD-FNN_B 模块为GD-FNN_A 的复制,但是其算法的权向量W 会按照下文式(26)的自适应率进一步调整,从而补偿广义动态模糊神经网络学习算法(GD-FNN)的建模误差;GDFNN_B 接受参考模型输出的rd、r˙d,输出补偿的控制信号ufnnb,和类PD 控制的输出控制信号一起构成系统最终的控制信号u。这样就可以快速、准确地控制无人艇航向。
鲁棒自适应模糊神经网络控制器(RAFNCRM)的目的是使所有的闭环变量有界并且能够跟踪给定的期望信号ψd。因为式(1)是一个二阶船舶运动操纵系统模型,根据参考文献[19]所述,其具有理想性能的参考模型应如式(10)所示:

式中,ψd为参考模型给出的期望航向角,ψr为模型参考信号系统的输入,ωn为系统的自然频率,ζ为系统的相对衰减系数。
为了跟踪期望信号ψd,定义如下的跟踪误差e和跟踪误差向量E:

由式(4)提出的逆动态模型和文献[20]的反馈线性化方法,可以得知理想的控制率u*为

从式(13)可以得知,如果适当地选择K,跟踪误差将收敛到零。然而,无人艇的外部干扰是随机无序的,无法准确地用简单的模型去描述。因此,为了解决这个问题,本文用GD-FNN 逼近理想的控制率,结合图2所示,本文理想控制率为

鲁棒自适应模糊神经网络控制器(RAFNCRM)的实际控制率为

式中,WTΦ为GD-FNN_B模块输出,Ke为类PD模块输出,取Ke = k1( )
ψr- ψ - k2r。
由式(2)、式(14)和式(15)可以得出无人艇航向跟踪误差为

式中,

再将式(14)和式(15)代入式(16),可得

式中,

为Hurwitz 矩阵。由式(18)可知,为了最小化跟踪误差,需要进一步调整权值向量W,因此,设计自适应率为

式中,γ是一个正常数,P是对称的正定矩阵且满足如下关系:

式中,Q 为选定的对称正定矩阵。为保证无人艇航向控制的稳定性,GD-FNN 必须收敛,同时也要求GD-FNN的参数有界,根据文献[21]的投影算法,将式(20)的自适应率修改为

2.3 稳定性分析
以下证明对于形同式(2)的非线性动态系统,在具有式(15)的控制率和式(22)的自适应率下,该系统一定是渐进稳定的。
证明定义基于式(18)的Lyapunov函数:

3 仿真实验
仿真实验采用某无人艇参数构建航向操纵运动模型[17],使用的风浪流干扰参数等相关设置如表1所示。在风浪流的干扰下,对上述研究中提出的基于广义动态模糊神经网络(GD-FNN)的鲁棒自适应模糊神经网络控制(RAFNCRM)进行了半物理仿真实验,同时与PD控制器对比,验证其正确性和有效性。

表1 无人艇操纵运动模型参数设置Tab.1 Parameter setting of maneuvering motion model of USV
半物理仿真实验中,使用真实的桨舵系统和控制系统,使用计算机仿真实际运行环境和传感器反馈数据,其相较于纯虚拟仿真实验更能体现出设备的性能对于控制算法的影响。
阶跃航向控制规定目标航线角为30°;方形航向控制每间隔20 s 改变一次航向角,改变幅度为30°;正弦航向控制周期为30 s,振幅为30°。分别在以上三种情况下与传统PD 控制进行对比,三种情况下设定航向、PD航向和RAFNCRM航向仿真结果如图3~5所示。
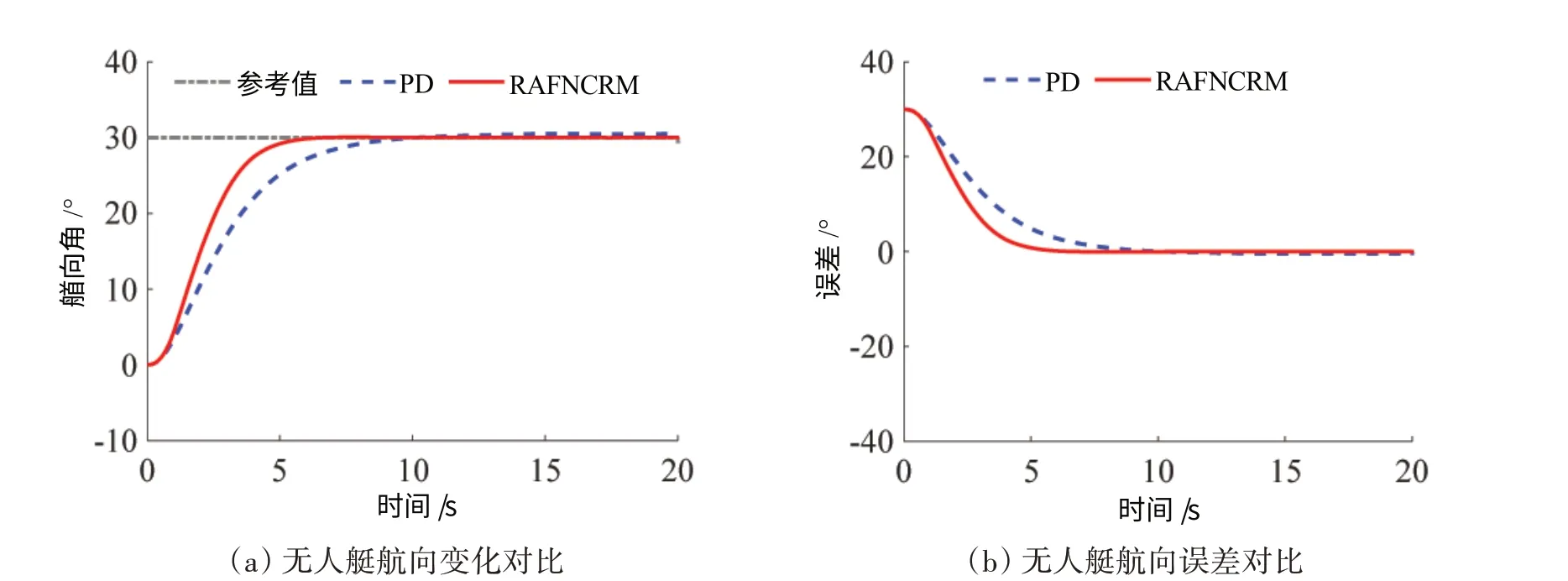
图3 无人艇30°阶跃航向控制对比Fig.3 Comparison of 30°step heading control for USV

图4 无人艇30°方形航向控制对比Fig.4 Comparison of 30°square heading control for USV

图5 无人艇30°正弦航向控制对比Fig.5 Comparison of 30°sinusoidal heading control for USV
图3为无人艇30°阶跃航向控制仿真图,优化后PD控制参数为:Kp= 1,Kd= 1。可以看出,采用基于广义动态模糊神经网络的鲁棒自适应控制器(RAFNCRM)的无人艇经过约7 s的学习调整,产生了5条推理规则,最终航向误差趋于零,对比项优化后的PD 控制的无人艇则经过约10 s达到期望值,且稳定后具有稳态误差约1°,误差难以趋向于零。
图4 为无人艇30°方形航向控制仿真图,优化后PD 控制参数为:Kp= 1,Kd= 1。图4 表明,在方形航向控制中采用基于广义动态模糊神经网络的鲁棒自适应控制器(RAFNCRM)的无人艇相比PD控制具有更快的调整速度,稳定后具有更小的稳态误差,基于广义动态模糊神经网络的鲁棒自适应控制器(RAFNCRM)产生了8条推理规则,学习时间约为7 s。
图5为无人艇30°正弦航向控制仿真图,优化后PD 控制参数为:Kp= 3,Kd= 0.5。经过约8 s的学习调整,基于广义动态模糊神经网络的鲁棒自适应控制器(RAFNCRM)产生了15条推理规则,成功地跟踪了正弦航向调整,且误差较小,对比项PD控制则在跟踪正弦航向时有较大的跟踪误差,误差在0~3°。可以看出,RAFNCRM控制器具有更少的调整时间和更准确的调整结果。
综合图3~5可以发现,在风浪流干扰下,基于广义动态模糊神经网络的鲁棒自适应控制器(RAFNCRM)在阶跃航向、方形航向和正弦航向控制中,均较好地完成了航向控制,且展现了比PD 控制更好的快速性和准确性,在比PD控制更少的时间内,达到了比PD控制更好的控制效果。仿真实验成功验证了该控制器的正确性和有效性。
4 结 论
针对无人艇高速航行过程中航向控制具有复杂非线性特征,且易受外界环境干扰影响产生抖动振荡等问题,本文提出了一种基于广义动态模糊神经网络的附加参考模型的鲁棒自适应控制器(RAFNCRM)方法,且基于Lyapunov 稳定性理论证明了控制器的稳定性和收敛性,并在风浪流干扰的环境条件下进行了半物理仿真实验,且与PD 控制方法进行了效果对比,验证了文中提出的鲁棒自适应控制器的有效性和准确性。研究结果表明:
(1)广义动态模糊神经网络有较强的在线自学习能力,能快速准确地逼近复杂的非线性动态系统;
(2)基于广义动态模糊神经网络的鲁棒自适应控制(RAFNCRM)具有较强的收敛性和稳定性,能够保证系统误差快速准确地收敛到零;
(3)采用基于广义动态模糊神经网络的鲁棒自适应控制(RAFNCRM)的无人艇能够快速学习外界的风浪流复杂干扰,降低环境干扰对无人艇航向控制的影响,具有较强的鲁棒性;
(4)无人艇使用基于广义动态模糊神经网络的鲁棒自适应控制(RAFNCRM)相比传统PD 控制可以更加快速、准确地完成航向调整控制,且随着时间推移,无人艇的航向跟踪误差可以近似收敛到零。

