基于深度置信神经网络的半潜式平台浮体运动模型和响应预测研究
陈 海,李志刚,冯加果
(1.北京邮电大学经济管理学院,北京100876;2.中海石油(中国)有限公司,北京100010)
0 引 言
半潜式平台是海洋油气开发的主力装备,典型的半潜式平台主要由上部结构、浮筒、系泊、管缆等水下结构组成。在复杂的海洋环境作用下,半潜式平台浮体的运动响应呈现出非线性和非平稳特性,大幅的平动和转动直接影响平台的作业和生产安全[1-6]。分析并准确预测平台浮体在耦合海洋环境荷载下的运动状态具有工程意义和科学价值。
目前,对于海洋浮式结构的科学研究主要集中于平台系统的水动力学性能等方面。Astfalck等[7-9]利用贝叶斯理论对FPSO 的极端响应进行分析,建立了时域极值的预测方法;Ng 等[10]基于势流理论和莫里森公式,运用数值分析和试验分析的方法对半潜式平台的运动响应进行了研究,分析了平台纵荡、垂荡和纵摇的响应幅值算子(Response Amplitude Operator,RAO);Yilmaz等[11]分别应用了频域和时域的分析方法对半潜式平台运动响应进行了模拟分析;潘子辉等[12]基于三维势流理论,利用数值计算和模型试验相结合的方法,对我国南海某半潜式平台的运动响应特点进行分析研究,对设计前期性能研究具有较高的参考价值;冯爱春等[13]采用时域分析方法研究了半潜式平台在不规则波作用下的动力响应特性,重点分析了在一根锚链断裂下平台浮体受不同浪向作用的运动谱和锚链张力谱特性。可以看出,基于水动力学数值仿真和模型试验的分析方法仍是当前海洋工程载荷和结构分析的主要研究手段。由于海洋环境模型的不确定性和平台浮体尺度的复杂性,利用上述方法开展平台浮体的准确预测仍较难得到满意的结果。近年来,以深度学习为代表的机器学习方法引起了广泛的关注。深度学习以含多隐层的多层感知器构成了深度学习的主体结构,模拟人脑的特征分析图像、声音和文本等,通过组合低层特征实现抽象的表征属性类别或特征的功能。其优势是可利用带有深度的多层流向图形式逐层提取和描述属性特征,因而对于高度非线性问题的回归和分类具有明显的优势。
本文以南海某半潜式平台的原型监测数据为基础,开展了对于平台浮体运动响应的深度学习模型化研究,对浮体的运动响应和分布规律进行预测。首先按照10 min为时间间隔提取了风、浪荷载监测信息的分布规律拟合参数,并结合分形学理论及统计分析的方法,提取了环境数据的特征参数,结合海流实测剖面数据建立了具有降维特征的荷载输入层。进而利用平台浮体的实测运动响应数据,分析了以10 min 为间隔的平台浮体六自由度运动响应的分布规律,提取了浮体响应的分布拟合参数作为特征参数。然后,基于深度置信神经网络(Deep Belief Network,DBN)方法建立了极端海况下海洋环境荷载与浮体运动响应的深度学习模型,同时开展了平台浮体运动响应和分布规律的预测研究,并与BP、DNN 等神经网络模型的预测结果进行了对比。最后,基于DBN 神经网络建立了海洋环境荷载特征参数与平台响应分布拟合特征参数的深度学习模型。
1 海洋环境荷载特征提取
1.1 海洋环境荷载信息原型监测简述
本文所用数据来源于2011 年以来在“南海挑战号”半潜式平台(NHTZ FPS)建立的现场监测系统[14-15],整个监测系统由海洋环境荷载要素、浮体运动响应以及系泊系统姿态监测三部分组成。其中环境监测子系统测量了风参数(风速、风向)、海流参数(流速、流向)和波浪参数(有义波高、谱峰周期和波浪压力)。表1 给出了各海洋环境荷载监测信息及采样频率,图1 所示为“南海挑战号”现场监测系统。

表1 海洋环境监测信息Tab.1 Monitoring information of ocean environment

图1 南海“挑战号”半潜式平台原型监测系统Fig.1 Diagram of“NHTZ”FPS prototype monitoring structure
1.2 海洋环境载荷特征参数提取
环境荷载参数选取是建立荷载和浮体运动响应模型的关键。基于风速和波浪压力的分形统计特征,选取计盒维数、Hausdorff维数及分布拟合参数作为特征参数。
1.2.1 随机变量的分形维数
分形维数是描述随机变量几何对象特征的重要因素,其本质是确定几何对象中一个点的位置所需的独立坐标数目。分形维数的定义式为

式中:D 为分形维数;l 为变换倍数,为该对象变换得到最终形态所经历的次数;N 表示变换后的个数,为变化后几何对象的个数。传统的分形维数可分为计盒维数和Hausdorff维数两类。
计盒分形维数表示为

Hausdorff维数表示为

对于特定监测时间序列{ }xi,i = 1,2,…,n,取时间段τ = tn- t1,则该时间段的序列均值xτ记为

在时刻tj,j = 1,2,…,m,时间序列的累计偏差为

幅值R( τ )为

1.2.2 风、浪荷载的分布特征规律提取
对于具有高采样频率、变化模式复杂等特征的风、浪环境荷载,其分布特征规律可以表征其载荷的时变特性。深入研究并选取准确的分布拟合参数可以提高深度学习模型的泛化能力。
以风速为例,设风速时间序列{ }xwind,i,i = 1,2,……,n,取某一时间段τ = tn- t1的风速时程xwind,τi分析其分布规律。经过对多组风速数据的分析,风速序列均满足Weibull 分布特性。Weibull 分布的概率密度函数表示为
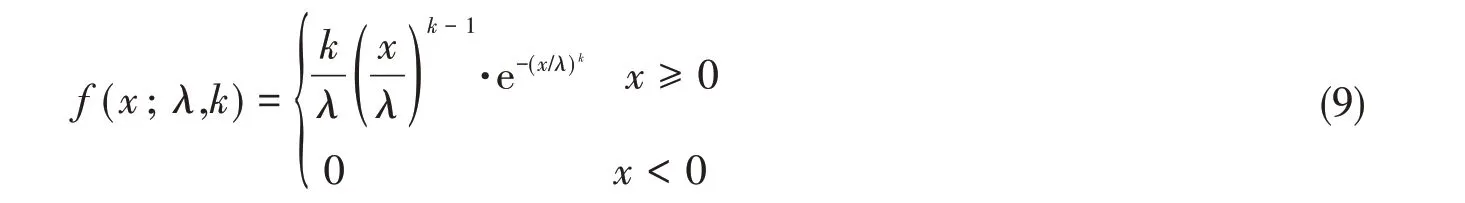
式中,x为随机变量,λ >0是比例参数,k >0是形状参数。对于任意时间序列xti,可选取其λi与ki作为风速的特征参数之一。
同理,对监测得到的波浪压力时程进行分布规律研究,波浪压力序列均满足正态分布特性。正态分布的概率密度函数为

式中,x为随机变量,μ为位置参数,σ为尺度参数。选取μ、σ为波浪压力分布拟合特征参数。
2 平台浮体运动响应分布特性分析
2.1 平台浮体六自由度响应监测信息
在复杂海况下,平台浮体产生的剧烈非平稳六自由度运动行为,可能对平台作业和人员安全带来威胁。现场监测过程中,平台浮体的六自由度响应主要通过GPS/INS惯性导航系统组合测量[17-18]。
表2 给出了平台浮体运动响应监测信息和对应的采样频率。
2.2 浮体运动响应分布特征参数提取
由于篇幅限制,本文以横摇为例描述浮体运动响应的参数提取方法,其他五个自由度分析方法类似。
针对横摇时间序列{ }xroll,i,i = 1,2,…,n,取一时间段τ = tn- t1,本文τ = 10 min,通过xroll,τi时程分析横摇的分布规律。

表2 浮式平台运动响应监测信息Tab.2 Monitoring information of the motion of the floating platform
分别选取不同时间段的横摇时程,从图2可以看出,横摇序列均满足正态分布特性。
正态分布的概率密度函数为

式中,x 为随机变量,μ 为位置参数,σ 为尺度参数。对于标准正态分布来说,μ 为该时间序列内x 的均值,σ 为该时间序列内x 的方差。通过μ 的大小可以反映该时间序列内横摇运动所处的运动工况,其中绝对值大小代表均值的大小,正负代表横摇的方向。其大小主要由风倾力矩引起,当均值较大时,说明其处于运动较为危险的工况下。
σ的大小可以反映该时间序列内横摇运动的整体水平和复杂程度。
通过选取不同时间段的横摇时程,横摇序列均满足正态分布特性。因此选取μ、σ 为响应分布拟合特征参数。
3 基于深度学习神经网络的平台浮体运动响应预测模型
3.1 深度置信神经网络(DBN)
本文所采用深度置信网络[19]是一种生成型深度学习模型,通过训练模型神经元间权重让整个神经网络按照最大概率来拟合训练数据。受限玻尔茨曼机(Restricted Boltzmann Machines,RBM)是深度置信网络的主要元件。样本训练时逐层进行,每层用显示层来推断隐藏层,当前的隐藏层作为下一层的显示层。
受限玻尔茨曼机的显示层和隐藏层之间全连接,每一层内部无连接。当显示层的神经元(显元)值确定后,每个隐藏层神经元(隐元)的取值没有任何关联。因此满足如下关系:

同样的,当隐元值确定时,显元取值也互不相关,有

式中,ν为显元值,hj为隐元值。
在深度学习模型建立过程中,首先以玻尔茨曼机进行无监督预训练,再以目标输出作为监督信号构造损失函数,通过梯度下降法对网络进行有监督的训练[20],最终形成具备高精度、高收敛性的深度学习模型。
3.2 极端海况下海洋浮式平台运动响应深度学习模型及预测
(1)数据来源
选取台风“天鸽”的监测数据作为训练和测试集,输入层为风速、风向、流速、流向、浪高和波浪周期六类数据。输出为横摇、纵摇、艏向角、海拔高度、纬度和经度,即反映平台运动特性的六类数据,样本数为600。
(2)建模过程
将环境荷载作为输入特征,平台六自由度运动作为输出特征。其中模型隐藏层共三层,每层节点数为10,Dropout 设置为0.9,正则化参数为0.01,学习率为自适应学习率。优化函数选择Adam 优化器,训练次数为500次。
(3)结果分析
选择如表3所示的一组实测数据作为验证集,将预测结果与期望结果进行对比,结果如图3所示。

表3 检验集的输入与期望输出Tab.3 Input and expected output of inspection set
同时将DBN 预测结果所得误差与常用的BP 神经网络、DNN 神经网络所得误差进行对比,如图4所示。

图3 预测值与期望值对比Fig.3 Comparison between predicted values and expected values
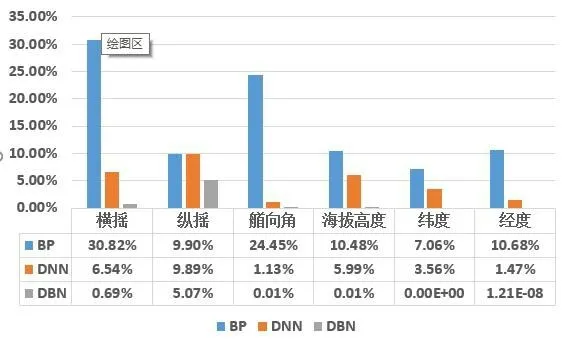
图4 DBN、BP、DNN误差对比Fig.4 Tolerance comparison of DBN,BP and DNN
表4 给出了三种神经网络模型的最大误差。通过对比可以看出,基于深度学习DBN 的神经网络模型计算结果误差最小,持续保持在较低的水准,表明了基于深层神经网络可以准确地描述海洋环境荷载与浮体响应间的强非线性映射关系。

表4 DBN、BP、DNN最大误差Tab.4 Maximum tolerances of DBN,BP and DNN
3.3 海洋浮式平台运动响应分布特征预测
响应分布特征是描述平台浮体在特定时间段内运动规律的重要指标,准确地预测平台响应分布可以获知平台在特定时间段内浮体运动响应的分布规律。为此,本节利用DBN 模型开展了运动响应分布规律预测,数据集选用2013.12.26 至2014.03.07 期间平台监测数据,该监测期间并无台风等极端海况过境,且平台也未发生移井等行为。因此本模型适用于工作海况下平台相应分布特征的预测研究。
3.3.1 平台浮体运动响应的深度学习模型化
现场实测过程中,海流的最大采样时间为10 min,因此在建立输入层样本过程中,选取10 min 的荷载信息作为样本输入的标准时间段,选取如表5 所示的载荷特征参数作为荷载样本的输入集。
其中风速和波浪压力信息的特征参数选取包括了可直观反映风速和压力时间变化范围的平均强度最大值、最小值及平均值等统计特征参数;同时选取了反映时间段内的风速及压力随机特性的计盒维数及Hausdorff维数等分形维数;还选取了风、压力的分布拟合函数以体现其时空分布特性。波高、周期、流速、流向选取实测数据作为特征参数。最终海洋环境载荷的样本集参数包含了分形维数、统计值以及力学特征参数等,全面包含了海洋环境荷载特性。
为了研究海洋平台运动响应的分布规律,选取了平台分布特征参数作为响应的特征参数。同时,为了分析深度学习模型方法在浮体响应预测的能力,选取了两种常用的神经网络模型(BP 和DNN 神经网络)作为对比,进行浮体六自由度响应的对比分析。
3.3.2 DBN建模过程
和平台响应预测方法类似,建模过程选用运动分布特征参数为模型输出指标,建立荷载特征参数与平台响应分布特征参数的深度置信神经网络模型。为了避免各个指标的含义和数值范围差异带来的计算不收敛和部分神经元提前饱和状态等问题,首先对样本数据进行了压缩处理。对于荷载特征参数及相应分布特征参数进行标准化处理,其公式为

选用5 个隐藏层的DBN 模型,每层神经元节点数分别为100、75、50、20 和10。以横摇为例,输出层节点数为2,即横摇分布特征参数,训练次数为500次。
3.3.3 分布参数验证
利用归一化数据进行训练,样本集总数为10 000,其中90%用于训练,10%用于检验。由图5~6可知,随着训练次数的增加,损失值随之快速下降并收敛到0.1左右,表明DBN模型有效地避免了局部收敛的问题。

表5 环境荷载样本特征参数Tab.5 Environmental load characteristic parameters

图5 RMSE随训练次数变化图Fig.5 RMSE changes with the iteration

图6 Loss随训练次数变化图Fig.6 Loss changes with iteration
进一步选取未训练的样本作为检验集。图7~8给出了期望数据与预测数据的对比结果。对比可知,所建立的浮体响应分布特征参数DBN神经网络模型可以获得准确的预测结果。
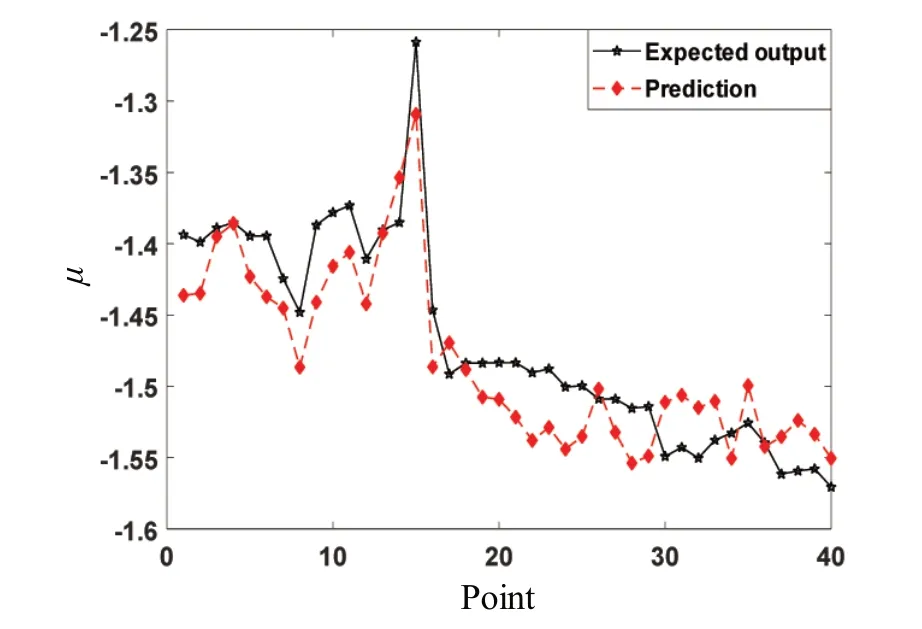
图7 μ预测结果与期望输出对比曲线Fig.7 Comparison of μ between predicted results and expected output
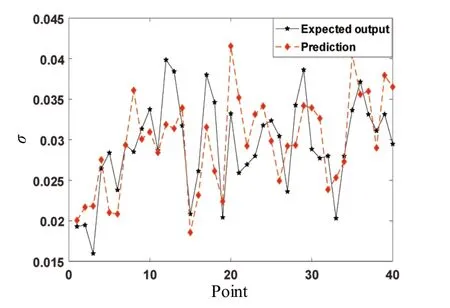
图8 σ预测结果与期望输出对比曲线Fig.8 Comparison of σ between predicted resultsand expected output
表6给出了期望结果与预测结果的误差分布,其中绝对误差公式为

由表6 可以看出,横摇响应的分布函数参数预测结果的绝对误差为0.054 1和0.009 3。
图9~10 给出了利用预测结果所重构的响应概率密度分布和累计概率密度分布,并和实测响应概率密度曲线的对比。可以看出,预测结果与实测结果具有较高的吻合度,进一步表明了DBN模型可实现对于平台响应分布的准确预测。

表6 DBN模型预测误差Tab.6 Predicted tolerance of the DBN model
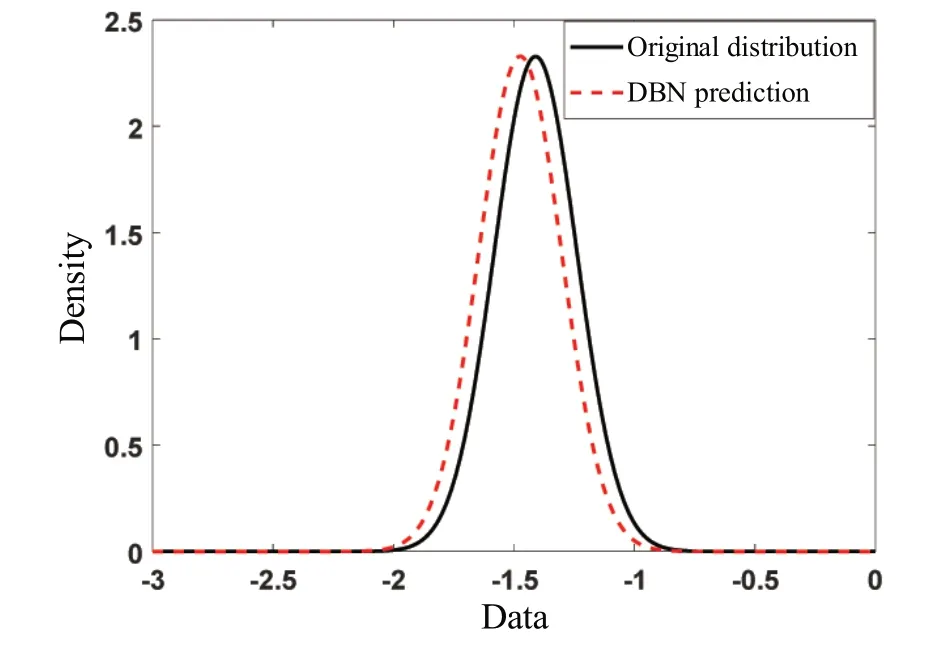
图9 概率密度曲线对比Fig.9 Comparison of the probability density curve

图10 累计概率分布曲线对比Fig.10 Comparison of the cumulative probability distribution curve
3.3.4 不同深度学习方法对比
和4.2 节类似,选用DNN 与BP 两种传统神经网络方法构建了海洋环境荷载参数与浮体横摇分布拟合特征参数的关系模型,其中DNN共有两层隐藏层,隐藏层节点数分别为50和10,输出层节点数为2(响应分布拟合特征参数)。BP神经网络共有1层隐藏层,隐藏层节点数为50,输出层节点数为2(响应分布拟合特征参数)。训练次数为500次。
图11~12 给出了DBN、DNN 和BP 神经网络的横摇分布函数参数的对比结果。对比可知,基于DBN模型的海洋环境荷载特征参数与响应分布拟合特征参数关系更为准确。

图11 不同方法μ预测结果对比Fig.11 Comparison of the prediction results of μ based on the different methods
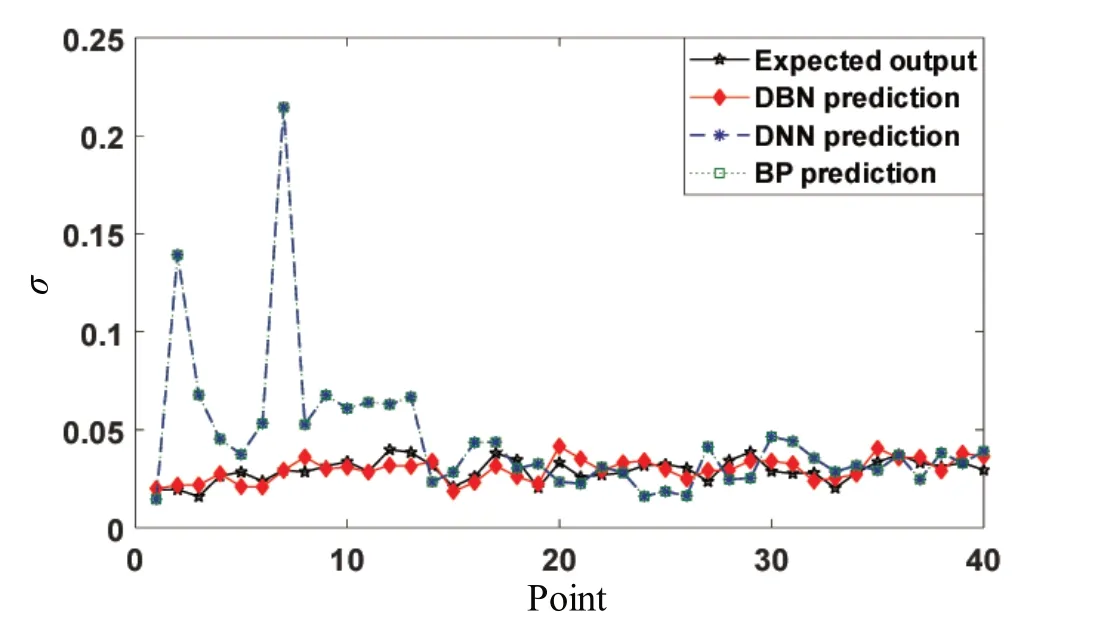
图12 不同方法σ预测结果对比Fig.12 Comparison of the prediction results of σ based on the different methods
从表7 所给出的三者误差对比中可以更明确地看出DBN 方法可以实现更高精度的响应参数预测。DNN 与BP 神经网络的预测结果一致,最大误差均为0.295 4 与0.185 1,表明基于DNN 与BP 神经网络的关系模型均出现局部收敛的情况,而基于DBN 神经网络的关系模型很好地规避了局部收敛的问题。
同时将检验数据进行分段分析,μ代表着横摇的运动幅值,将检验集的μ划分为两个区间。其中(-1.5,-1.6)表示横摇运动幅度较大;(-1.25,-1.45)则表示横摇运动幅度较小(正负代表运动方向)。图13 给出了不同区间内不同方法的对比结果。由图13(a)可以看出,在(-1.25,-1.45)区间内DBN 的预测结果与DNN 与BP 的预测结果相差不大,均存在一定的误差,说明在横摇运动幅值较小的情况下,DBN 模型的预测结果相较于DNN 与BP 模型的结果优势不大。而由图13(b)可以看出,在(-1.5,-1.6)的区间内,DBN 预测结果可以实现更高的精度,而DNN 与BP 的预测结果均偏小,说明在横摇运动幅值较大的情况下,DBN 模型也可以对横摇的分布规律进行预测,而DNN与BP的结果误差较大。

表7 不同模型的误差对比Tab.7 Tolerance comparison of the different models
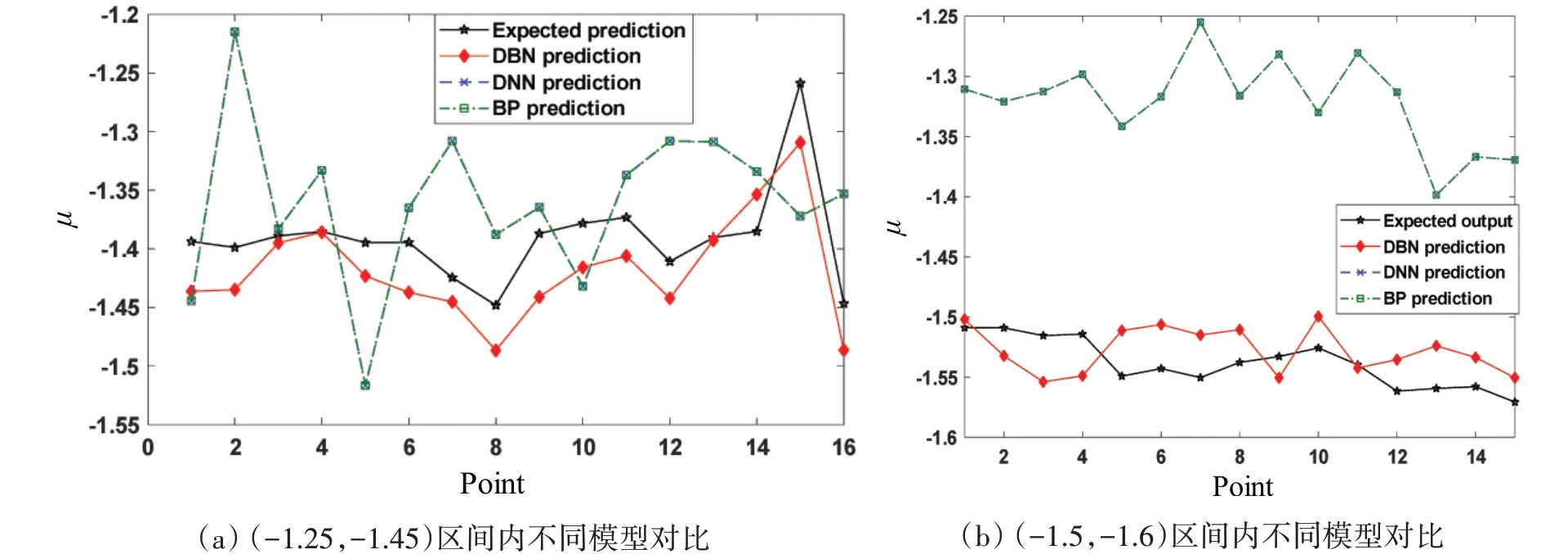
图13 μ在不同区间内DBN、DNN与BP模型预测结果对比Fig.13 Comparison of the prediction results of μ in different intervals based on the different methods
表8 给出了不同区间内不同模型的预测误差,在(-1.5,-1.6)区间内,DBN 模型的最大误差为0.038 4,而DNN 与BP 模型的最大误差均为0.295 4,约为DBN 模型的8 倍,说明在横摇运动幅值较大的情况下,DBN 模型的预测精度要远大于DNN 与BP 模型。在(-1.25,-1.45)区间内,DBN 模型的最大误差为0.054 1,而DNN 与BP 模型的最大误差为0.184 0,约为DBN 模型的3 倍左右,同时也仅为(-1.5,-1.6)区间最大误差的三分之二。说明在横摇运动幅度较小的时候,DBN 模型仍可以取得较高的精度,同时DNN 与BP 模型预测结果也好于横摇运动幅度较大的时候。
为了进一步验证不同模型的预测效果,随机选取两组典型期望结果与预测结果代入高斯密度函数中(公式(11)),图14给出了两组期望结果与预测结果下的概率密度曲线与累计概率分布曲线。可以看出,基于DBN 的关系模型给出的预测概率密度曲线与实测概率密度曲线最为接近,而基于DNN 与BP 的关系模型给出的预测概率密度曲线与实测概率密度曲线误差更大且峰度偏度均不相同。
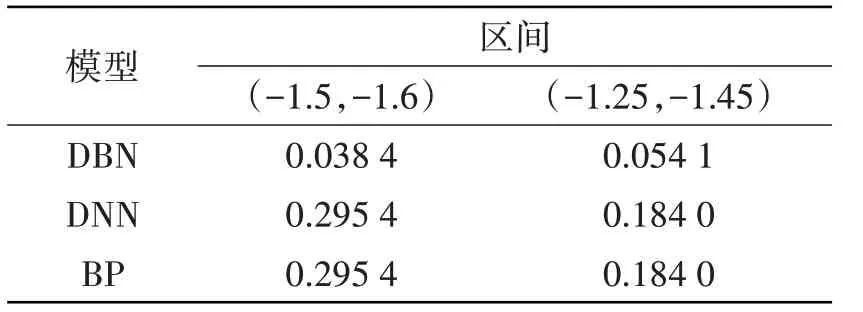
表8 不同区间内不同方法的误差对比Tab.8 Tolerance comparison of the different models

图14 不同方法概率密度分布曲线与累计概率分布曲线Fig.14 Probability density distribution and cumulative probability distribution based on the different methods
4 结 语
本文利用在中国南海某半潜式平台实测海洋环境荷载数据和平台响应数据开展了基于深度学习的模型化方法研究,建立了基于DBN 神经网络的浮体响应和分布规律预测方法,对比了传统BP 和DNN神经网络方法,获得了准确的预测结果,可以为平台的作业提供辅助支持。
对于风、浪载荷进行了特征参数选取研究,本文依据其分形特征和统计特性,发展了一种基于海洋环境荷载的特征参数选取方法。对于平台浮体响应特征,进行了运动响应的分布特性研究,选取每种响应的分布拟合参数作为响应特征参数。
本文利用“天鸽”台风的监测数据,建立了基于DBN 极端海况下平台环境信息与平台六自由度运动的关系模型,并进行了模型检验分析,可以看出,最大误差仅为5.07%。并与BP、DNN等模型结果对比分析。结果显示,基于DBN的海洋环境荷载与平台运动响应的关系模型结果更为准确,最大误差仅为5.07%。
本文利用长期监测数据,建立了基于DBN 的环境特征参数与平台浮体横摇响应分布特征参数的关系模型,该模型检验误差仅为0.054 1与0.009 3。并对不同区间内预测结果进行分析,可以看出,在横摇幅值较大的情况下,该模型仍能保持较高的精度。所建立的平台浮体运动响应分布特征参数模型可以准确地预测浮体运动响应的分布规律,为分析海洋浮式平台的动力学特性提供基础。

