基于LSTM网络的浮式海洋平台运动在线预报研究

李昊波，肖龙飞,2，魏汉迪,2，刘明月,2

（1.上海交通大学海洋工程国家重点实验室，上海200240;2.高新船舶与深海开发装备协同创新中心，上海200240）

0 引 言

随着海洋开发规模与领域的不断扩大，船舶和海上平台等浮式结构物的重要性日益凸显。与固定或陆地上的结构物不同，海上浮式结构物始终处于多自由度摇晃中，使其海上作业和安全都受到严峻的挑战。因此，对海上浮式结构物的运动进行准确可靠的在线预报，在指导作业、保障安全等方面具有重要意义。

运动在线预报一般基于运动历史数据采用时间序列分析方法、非线性系统理论、机器学习技术等手段预报未来几秒到几分钟的海上浮式结构物的运动响应[1]，可分为极短期运动预报和安稳期预报。对浮式结构物的极短期运动响应预报在固定翼舰载机回收、提高舰载武器发射精度、改善动力定位控制性能等方面均具有重要意义。

极短期预报提前量一般为几秒，相对较短，但对预报精度要求较高。按照采用的数学方法分类，可以把极短期预报分为两类：其一是以传统的物理和数学方法如微积分和统计学等为基础的预报模型，有时间序列模型、卡尔曼滤波模型等；其二是以神经网络、模糊数学等现代方法为手段的模型，如神经网络模型、小波分析预报模型等[2]。Triantafyllou 等[3-4]利用Kalman 滤波技术为基础的方法对船舶的6 个自由度运动进行预报，发现有义波高、艏摇和噪声等因素对预报精度影响很大，在无噪声情况下横摇可预报到10 s，在有噪声情况下可预报提前量仅为2～3 s，且预报误差没有给出[4]。Khan 等[5]采用人工神经网络技术对横摇运动进行了预报，预报提前量为6 s 时可信度为60%，预报提前量为10 s时可信度仅为40%。Huang等[6]基于AR-EMD 方法对船舶纵摇和垂荡运动进行了极短期预报，在预报提前量为10 s 时，精度分别为85%和84%。Peng 和Liu[7]基于格型递归最小二乘法对船舶横摇运动进行了预报，在预报提前量为15 s时，精度为81%。杨震等[8]基于经验模式分解，利用支持向量机对船舶横摇运动进行预报，预报提前量为10 s时的误差为0.09。目前关于船舶的运动预报较多，而关于浮式海洋平台的运动预报较少，尤其是纵荡、横荡运动。总体上，在线预报目前表现一般，模型计算复杂度高，误差随预报提前量增加而非线性增长，难以实用。本文根据近年来广泛应用的长短期记忆（LSTM）神经网络技术提出一种新的运动预报模型，应用于浮式海洋平台运动响应的极短期预报，在保证计算效率的情况下，可以得到准确的运动预报结果。

1 LSTM 模型

1.1 循环神经网络和LSTM

浮式海洋平台在实际不规则波环境中的六自由度运动响应具有很强的随机性、非线性以及时间依赖性，传统的数学、力学方法求解复杂费时，很难应用于需要实时获得响应数据的运动在线预报。神经网络技术则十分适合用于此类问题，即模拟一组数据到另外一组数据的映射。本研究的思路为：把不规则波浪时历到运动响应的映射看成是一种复杂的、未知的映射函数，使用神经网络来拟合此函数，最终得到输入为波浪时历，输出为运动响应的神经网络模型。

针对浮式海洋平台运动响应的预报，传统的神经网络模型尚难以实现。这是因为海洋平台在t时刻的运动响应不仅取决于该时刻的波浪作用，还取决于t-1时刻海洋平台的状态；而t-1时刻海洋平台的状态同样不仅取决于t-1 时刻的波浪作用，还会受到t-2 时刻海洋平台状态的影响，依次类推。因此，浮式海洋平台的运动响应具有时间依赖性，若要准确预报海洋平台的运动响应就需要把随时间传递的信息应用到预报模型当中。循环神经网络（RNN）恰好可解决这一问题，在处理时间序列相关的数据方面具有很好的效果。

RNN 的单元展开图如图1所示，x为网络输入，s为隐藏层，o为网络输出，U 为输入到隐藏层权重，V为隐藏层到输出权重，W 为隐藏层到隐藏层权重。与传统神经网络不同，在RNN 中每一层网络共享权重，这样会有效地减少网络中需要训练的参数，缩短了训练时间。但RNN 存在梯度消亡问题，来自之前的记忆信息对输出的影响会逐渐衰减趋于消失或者呈指数爆炸增长，从而严重影响模型的收敛速度与性能。

LSTM最早由Hochreiter和Schmidhuber[9]提出,并经由Grave[10]改进，有助于解决RNN的梯度消亡问题。LSTM 的单元结构[10]如图2 所示，每个LSTM 单元中存在细胞（Cell）用于描述单元当前状态，也存在3 个控制门，即输入门（Input Gate），输出门（Output Gate）和遗忘门（Forget Gate），分别用于控制输入、输出以及细胞的状态。当控制门打开时，表示允许所有信息通过；控制门关闭时，表示不允许任何信息通过。其方程如下：

式中，ft为遗忘门方程；ct为输入门方程，用以更新细胞状态；ot为输出门方程，与ct共同输出ht。

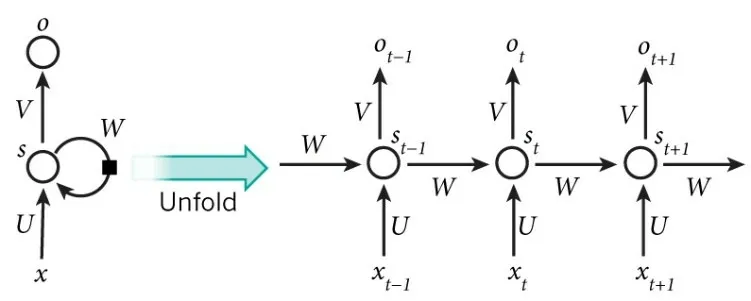
图1 循环神经网络单元展开图[11]Fig.1 An unfolded CNN network

图2 LSTM单元结构[10]Fig.2 LSTM memory block with one cell

LSTM 可归纳为图3 所示的几种类型，针对由波浪序列预报海洋平台运动问题，本文采用多对一类型，使用一串波浪序列预报一个运动响应值。图4解释了利用波浪序列预报运动响应的思路，显示了预报提前量为5 s的模型输入输出映射关系，t时刻的运动响应由t-15到t-5时间段的波浪序列预报得出。

图3 LSTM类型Fig.3 Types of LSTM

1.2 LSTM模型结构

本文所构建的LSTM 模型具有一层LSTM 隐藏层和一层输出层，如图5 所示。考虑到波浪和平台运动的周期，设置LSTM 模型的时间步长为128 个时间序列点，以及考虑波浪和运动之间映射的复杂度，设置LSTM 模型隐藏层节点数为256。此两项参数作为超参数，根据经验和实际尝试确定。

输入层：输入数据是长度为128 的向量，其物理意义是长度为128的波浪序列，代表此模型的时间步长被设置为128，输入特征维度为1。

隐藏层（LSTM）：隐藏层有256 个节点，其接受形状为（None，128，1）的输入，输出形状为（None，256）的向量。

输出层（Dense）：是一个全连接层，其输入数据为隐藏层（LSTM）输出的形状为（None，256）的数据，输出为运动响应值。

本文采用随迭代次数降低学习率的技巧来帮助神经网络模型的训练。学习率是调整神经网络的重要超参数之一，如果学习率过高，则会导致不收敛或者振荡现象产生。但是如果学习率过小，训练时间会较长，且会容易陷入局部最优。因此，令学习率随迭代次数降低是一种有效的解决方法。一旦验证集误差不再降低，学习率就会被设置为原先的十分之一。

另外，使用Dropout技巧防止过拟合[12]。Dropout主要将隐藏层中的神经元在每一次训练过程中按照一定概率进行丢弃，此部分权重在本次训练过程不进行更新，从而实现了“取平均”和减少神经元之间复杂的共适应关系的作用，可有效地防止过拟合的产生。

图5 LSTM网络模型结构Fig.5 LSTM model structure

2 海洋平台模型试验数据

本文训练数据来自于一座半潜式钻井平台的运动响应试验，试验在上海交通大学海洋工程国家重点实验室深水试验池进行。水池的几何尺度及平台模型布置如图6 所示，采用4 点水平系泊系统，系泊缆由细钢丝绳与软弹簧构成，与平台坐标轴成45°对称布置。考虑180°浪向，试验水深为10 m。所研究的半潜式钻井平台为典型的四立柱、双浮箱、箱型甲板型式，主要参数见表1，外形轮廓如图6所示。模型缩尺比λ为56。

图6 深水池布置及半潜式平台模型Fig.6 Deepwater offshore basin layout and the semi-submersible model

开展的不规则波试验共有40个工况，考虑4种海况，如表2所示。其中不规则波W1与W2各4个随机时间序列，W3 与W4 各16 个随机时间序列。试验采样频率为100 Hz，每个工况测量得到的试验数据超过160 000 点，保证了训练数据的充分性。采用所建立的LSTM 神经网络模型，使用其中34 个不规则波试验工况数据（W1 与W2 各3 个，W3 与W4 各14 个）对LSTM 模型进行训练，剩下的6 个工况数据用于测试神经网络模型预报运动响应的性能。

表1 半潜式平台参数Tab.1 Main particularities of the semi-submersible

表2 波浪环境参数（JONSWAP）Tab.2 Environment matrix（JONSWAP）

3 预报结果与分析

使用经过34个工况试验数据进行训练后得到的LSTM 模型，对迎浪状态（180°）6个测试工况下半潜式平台的纵荡、垂荡以及纵摇运动进行预报，预报提前量分别设置为0 s、6 s 和12 s。LSTM 模型的运动时历预报结果如图7～9所示，其中虚线代表试验的实测值，实线代表预报值。由于时间序列长度过于巨大，所以从时间序列起始、中间和末尾三个时间段各选取了300 s时间长度进行结果对比。

图7 不同预报提前量下的纵荡运动预报与测量结果对比Fig.7 Comparison between predicted and measured surge motions for different forecast durations

图8 不同预报提前量下的垂荡运动预报与测量结果对比Fig.8 Comparison between predicted and measured heave motions for different forecast durations

图9 不同预报提前量下的纵摇运动预报与测量结果对比Fig.9 Comparison between predicted and measured pitch motions for different forecast durations

从图7～9 可以看出，在各个预报提前量情况下，LSTM 模型对平台运动响应的预报结果均较为准确，预报值很好地拟合了实测值。不设置提前量的情况下，预报结果精度较高，在可以提前测量波浪的情况下，此模型具有很大的应用价值。在预报提前量为6 s的情况下，预报精度稍有降低，所以此模型可以实现对海上浮式结构物较高精度的极短期预报。而在预报提前量为12 s 的情况下，预报精度有所降低，但预报时间得以延长，使得此模型适用性更为广泛。同时可以看到，在预报提前量为12 s的垂荡预报情况下，存在相位差，这是由于起始数据都接近0 且预报时间偏长的原因，但由于振幅小且位于运动启动阶段，对实际应用影响可不考虑。

根据运动响应预报曲线和实测曲线的相关系数，可计算得到LSTM 模型对于测试工况的预报精度，结果如表3 所示。可见，尽管预报精度随预报提前量的增加而降低，然而在预报提前量为12 s时，纵荡预报精度仍为90%，垂荡预报精度可达93%，纵摇预报精度稍低，在85%以上。总体而言，运动预报结果具有较高精度，使用LSTM模型预报浮式海洋平台运动具有较高的可行性。三种运动响应预报的精度结果对海况和训练数据变化的敏感程度不同，从W1 至W4，波高逐渐增加，用作训练数据的工况数也从3 个增加到14 个，基于LSTM 模型的垂荡和纵摇预报精度也逐渐提高，而纵荡的预报精度始终较高，对海况和训练数据变化不敏感。

表3 不同测试工况下运动预报精度统计结果Tab.3 Prediction accuracy statistics under different test cases

运动响应的均方差表征了运动幅值的大小，表4 所示为不同测试工况下运动测量值与预报值的均方差结果对比。可见，三种运动响应预报结果的均方差均接近于测量值,纵荡均方差相对误差最小，纵摇结果的相对误差较大。预报值的均方差相比于测量值都偏小，表明所构建的LSTM 模型在预报运动响应时偏于保守。

表4 不同测试工况下运动测量值与预报值均方差对比Tab.4 Comparison of standard deviations between measured and predicted motions under different test cases

续表4

此外，计算效率是在线预报实时性的基础。使用神经网络模型进行运动响应的预报，在考虑预报精度的同时，还必须考虑计算效率的影响，即每一步的计算时间都应该远小于预报提前量。本文LSTM 模型的参数量为264 449，在个人电脑上平均每步计算时间约为10 ms，相对于预报提前量6 s和12 s而言极小，故模型计算效率可满足实际应用的实时预报要求。

4 结 论

基于机器学习理论，本文建立了浮式海洋平台运动预报的LSTM 神经网络模型，通过采用半潜式平台模型试验大量运动响应数据的学习训练，并对不同测试工况进行运动预报和分析，得到了不同预报提前量时的模型预报精度。结果表明：

（1）所建立的LSTM 模型应用于浮式海洋平台运动极短期在线预报具有较高的可行性，预报提前量为12 s时，纵荡、垂荡和纵摇预报精度可分别达到90%、93%和85%以上。

（2）所构建LSTM 模型在预报纵荡运动时的精度随海况和训练数据的变化不明显，而在预报垂荡和纵摇运动时的精度对海况和训练数据变化敏感，随波高和训练数据的增加而精度提升，模型预报运动响应结果偏于保守。

（3）LSTM 模型每步计算时间为毫秒级，远小于预报提前时间，实时性高，可以实现对浮式海洋平台运动响应的在线预报。在实际中，应用LSTM模型可以对浮式海洋平台的作业进行安全预报或主动进行提前控制，也可以拓展到船舶运动预报。