轴压柱形壳非线性屈曲试验与理论研究

王黎辉，李其凡，张 建，唐文献，朱永梅

（1.江苏科技大学机械工程学院，江苏镇江212003；2.江苏省船海机械先进制造及工艺重点实验室，江苏镇江212003）

0 引 言

圆柱形壳因其良好的承载力和易于加工等特性在海工平台应用广泛，目前平台桩腿多采用桁架式和柱壳式[1]。其中柱形壳桩腿工作时主要受到轴向载荷，非线性屈曲是其主要失效模式，且受壁厚、材料属性及几何缺陷等影响很大。

对于柱壳的轴压临界载荷，国内外学者围绕几何缺陷、材料属性等方面已经开展了大量的研究。Bardi 等[2-3]对轴压下柱形钢管的塑性屈曲性能进行了试验和理论分析；Lancaster 等[4]对端部约束的柱形壳在轴压时出现的矛盾现象进行了解释；Takla[5]利用连续理论发现柱形壳在外部压力载荷作用下加入拉伸或压缩轴向力，能够延迟分段失效分岔模式的发生；Papadopoulos等[6]证明了随机变化的轴向载荷对缺陷敏感结构(如轴向压缩薄壁圆筒)的屈曲行为具有重要影响；Błachut[7]对轴向缺陷的柱壳进行了研究，发现端部的长度缺陷对轴压屈曲载荷值影响大于其他制造缺陷，但是其研究柱壳一端无缺陷，而另一端以正弦曲线模拟缺陷，未对两端都出现不规则缺陷进行研究；Castro 等[8]研究了五种缺陷（单摄动载荷缺陷、模态缺陷、几何凹坑缺陷、轴对称缺陷及测量几何缺陷）对轴压复合材料柱形壳的影响；Ifayefunmi[9]对轴压金属柱形壳进行了试验，结合理论分析与数值分析研究了其屈曲行为，发现边界条件、试件材料属性以及试件加工过程都会对结果产生影响；Fan[10]研究了探测柱形壳以预测临界载荷的方法。然而目前关于固定厚径比、不同高度且端部自由的柱形壳轴压屈曲研究鲜见报道，这方面的理论和试验数据严重不足。

因此，本文从试验研究、理论分析和数值计算三方面研究高径比小于1，厚度半径比为0.03的柱壳在端部自由时受到轴向载荷时的屈曲行为。选用具有不同长度且在长度上存在缺陷的试件以研究轴向长度缺陷对屈曲特性和临界载荷的影响。同时利用数值计算结合试验研究，确定适用于此类柱形壳临界载荷计算的公式。研究结果对端部无约束且承受轴向力的柱形壳的设计具有理论意义和应用参考价值。

1 材料与方法

1.1 几何厚度与形状

304不锈钢为典型而常见的低碳钢，选取其为研究对象的材料具有代表性。柱壳的主要几何参数为外径D，厚度t以及高度L，令轴向为z轴方向，径向面为x-y面，如图1所示。

图1 不锈钢柱壳结构及试件样品Fig.1 Structure and samples of stainless steel cylindrical shell

研究的圆柱壳外径D=40 mm，名义厚度t=0.6 mm，高度分别为40 mm、30 mm 和20 mm，可以看出名义高径比不大于1。试验根据高度不同共分为3组，为保证数据可重复性，每组2 个试件，共6 个试件。第一组高度40 mm 的试件命名为L40_1、L40_2，同理，第二组和第三组命名为L30_1、L30_2、L20_1和L20_2。使用尖头千分尺（型号：青制00000003号，量程：25 mm，分度值：0.01 mm）对6 个模型测量壁厚，沿模型周向均分5 组，每组沿轴向测量5 个点位，共计25个点位厚度，测量结果列于表1。

表1 模型壁厚测量结果（单位：mm）Tab.1 Measured wall thicknesses of specimens

沿模型周向均分8 个点位，使用游标卡尺测量每个试件的外径和高度，测量结果如表2 所示，ΔL为长度最大值与最小值的差值。

表2 模型外径和长度测量结果（单位：mm）Tab.2 Measured outer diameters and lengths of specimens

1.2 材料参数及加工方法

材料为304不锈钢，是奥氏体不锈钢的一种。试验试件为使用砂轮切割机切割的圆柱钢管，后用锉刀去除毛刺，如图1 所示。在加工时利用直角尺保证轴线垂直，从而保证试验时试件沿轴心受压。因为采用砂轮切割机手工切割，所以在加工后端部存在随机的长度缺陷，测量长度与名义长度的差值l如图2所示。

304 不锈钢无明显屈服阶段，无明显屈服极限，因此以产生0.2%残余变形的应力值作为其屈服极限，测试3 次。0.2%残余变形应力值分别为351.15 MPa、363.00 MPa 和365.02 MPa，取均值得到屈服强度σyp=359.7 MPa。根据厂家提供的数据，该304 不锈钢的杨氏模量E=195 GPa，泊松比ν=0.247。

1.3 轴压试验

试验采用万能压缩试验机（型号：CMT-5305；试验力：300 kN；试验力测量范围：0.2%～100% FS；试验机分辨力：1/300 000 FS；有效压缩空间：800 mm；位移分辨力：0.015 μm；大变形分辨力：0.008 mm），试件置于平台中心，无需任何约束固定。将上端压头缓慢下调，稍与试件上端部接触后，开始正式压缩试验。轴向压缩速率为1 mm/min，压缩变形量为10 mm，利用高速摄影机记录柱形壳变形情况，图3 为L40_2 的变形状况。

图2 试件测量长度与名义长度差值Fig.2 Difference between the measured lengths and the nominal lengths

图3 试验过程产生鼓曲Fig.3 Bulge produced in the experiment

2 结果分析与讨论

2.1 测量结果分析

使用意大利Open Technologies 公司生产的Cronos 光学扫描仪（测量精度≤0.02 mm）对每个试件进行侧面轮廓扫描，获取真实侧面轮廓模型。使用三维检测软件GOM Inspect 对扫描结果进行误差检测。软件自动将扫描点云数据转化为三维网格数据，通过比较扫描数据和具有名义尺寸的CAD 数据以及分析假色图进行柱形壳侧面误差检测。误差检测结果如图4所示。

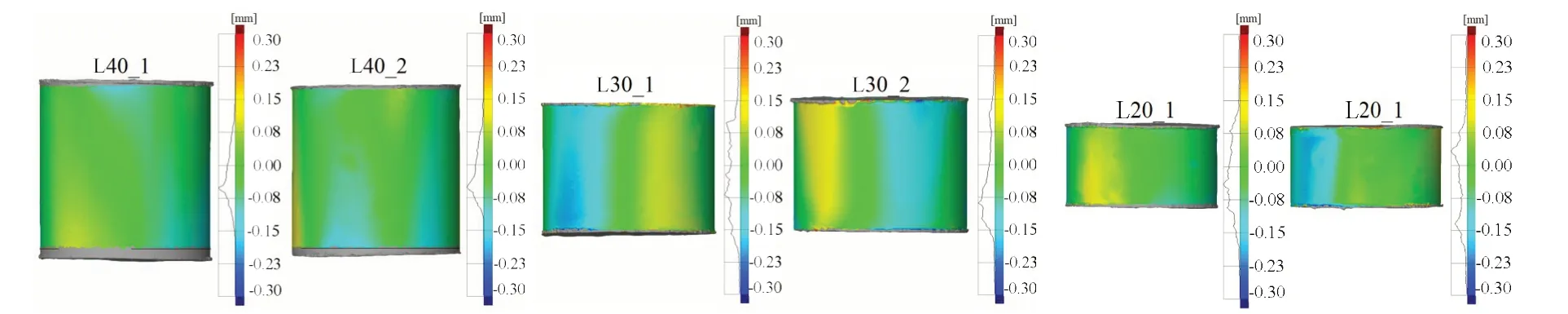
图4 实际壳体与理想模型尺寸误差结果Fig.4 Deviation between actual models and nominal models

如图4 所示，右侧数值带数据表示误差大小范围，曲线表示误差频数分布。由图可见，六个试件的误差基本在-0.2～0.2 mm 之间，绝对值为壁厚的1/3。通过表1 可以看出，模型的平均壁厚在0.582～0.590 mm 之间，略小于设计名义壁厚0.6 mm；测量厚度和名义厚度存在的最大误差为0.088 mm，且仅有一点，其余点位最小误差仅为0.03 mm，并且标准偏差值较小。因此可以认为，试验模型侧面形状与壁厚与设计模型基本一致。主要变化在于高度和端部的长度缺陷，所以忽略侧边形状误差，主要研究端部长度缺陷对屈曲行为的影响。

2.2 试验结果分析

计算机在轴压试验进行时采集位移载荷的数据，因仅研究第一次屈曲情况和临界载荷，故选取从轴压开始至屈曲发生，位移载荷曲线下降一段时间后的数据，即位移0～3 mm 时的变形状况，绘制图5的位移-载荷图。试验测得各试件的临界载荷值列于表3。

图5 试验位移载荷图Fig.5 Plot of load against compression extension for cylinders in the experiment

表3 试验试件临界载荷Tab.3 Critical loads of experimental specimens

如图5 所示，轴向压缩位移-载荷曲线经历了上升阶段（原点至最高点）、屈曲临界点（最高点）和屈曲失稳阶段（最高点至最后）。因为304 不锈钢韧性较高，所以未出现破坏阶段。在屈曲失稳临界点之前，轴向压力随压缩量的增大而较快上升，到达临界点后缓慢下降，且逐渐趋于平缓。由图可见曲线在压缩位移约0.2 mm 时会发生变化，这是由端面未完全约束且存在缺陷导致端面受力不均引起的，同时表明此时无需较大的轴向压力（图中不大于5 000 N）就会造成较明显的位移，可以认为此时长度缺陷削弱了柱形壳的承载力。继续进行压缩，可发现屈曲发生时柱壳一端会形成环状的鼓曲，并且同时有褶皱形成连接至鼓曲，有时褶皱会打断环状鼓曲的形成（多见于高度为20 mm），试验结果如图6 所示。此外，可见L20 组的试件，柱壳两端发生明显的形变，而L40 和L30 组只在一端发生明显的形变。

图6 轴压柱壳试验结果Fig.6 Axially-compressed cylindrical shells

2.3 试验与理论对比分析

柱形壳在轴压下的失效或屈曲特性由壳体的径厚比决定。通常情况下，薄壳易于发生弹性屈曲，所以设计准则基于屈曲失效；而厚壳失效在弹塑性变形时，所以设计准则基于断裂。对于圆柱壳的轴向压缩，如果压力均衡对称，则在圆周附近会出现一圈鼓曲。

经典柱形壳轴压屈曲分析是以忽略弯曲应力的Donnell薄壳理论为基础，此时可以得到柱壳的轴向压缩弹性临界屈曲载荷为

对于相对厚的柱形壳，因其失效在塑性变形区间，故参考临界屈曲载荷Fr采用引起柱壳屈服的载荷[11]：

式中，Fc为柱形壳经典弹性临界屈曲载荷，Fr为引起柱形壳屈服的参考屈曲载荷，E 为材料杨氏模量，σyp为材料屈服强度，ν为材料泊松比，D为柱壳直径，t为柱壳厚度。

本文试件的t/R=0.03，根据Zhang 等[12]对球形耐压壳的研究，虽然t/R=0.05是厚壳、薄壳的分界线，但是当t/R＜0.015时，薄壳强度理论方可适用于强度的初步评估。若将模型视为薄壳，则根据式（1）可得，Fc=265 611.9 N；若视为相对厚的圆柱壳，则根据式（2）可得，Fr=27 122.25 N。根据结果，可知若视为厚壳或薄壳，其临界载荷值相去甚远。

利用有限元软件Abaqus 进行无缺陷模型的线性屈曲分析，奥氏体不锈钢各向异性不明显，因此仿真时不考虑材料的各向异性。材料性能参数为：屈服强度σyp=359.7 MPa，杨氏模量E=195 GPa，泊松比ν=0.247。壳体底端固定，顶端沿边界施加向下的壳边载荷（shell edge load），初始载荷值取100，得到柱壳模型的失稳模式。壳单元类型为S4R。L40、L30 和L20 的壳单元数量分别为20 080、15 060和10 040。求解参数有：请求特征值数量为6，每次迭代向量数量为12，迭代步数为300。约束定义为：底端限制z方向自由度，即Uz= 0，顶端三个方向自由度均不限制，如图7所示。利用线性屈曲分析得到一阶失稳模式如图8 所示。由图可知柱壳在轴向压缩时，会在端部形成鼓曲，发生失稳，且会有在随机位置出现褶皱的趋势。线性屈曲分析无法考虑缺陷和非线性特性，仅能分析理想线弹性壳体的屈曲特性，所以要得到准确结果，必须经过非线性屈曲分析。

图7 数值分析边界条件Fig.7 Boundary conditions of numerical analysis

图8 一阶线性屈曲失稳模式及试验屈曲行为Fig.8 First eigenmodes of buckling and the experimental behaviors of buckling

利用Abaqus的Riks弧长法，对不同高度的无缺陷圆柱壳进行非线性屈曲分析，其基本参数有：初始弧长为0.01 mm，最大弧长为0.1 mm，最小弧长为1×10-50mm，总弧长为1 mm 的最大迭代步数为400。柱形壳体属于薄壳结构，壳单元类型选择S4。采用与线性屈曲分析相同的参数，得到各壳体数值分析的临界载荷。弧长法可以得到柱形壳模型屈曲过程的平衡路径，而平衡路径曲线中的极值点所对应的载荷即临界屈曲载荷。不同高度柱形壳所得的非线性屈曲临界载荷值、各组试验的临界载荷均值和理论分析值列于表4，临界载荷数值解与试验值之比列入表3。

3组分析所得的位移-载荷图趋势一致，如图9所示，以L40 为例，并与试件L40_1 的试验曲线比较，可见在屈曲过程中，实际载荷首先单调增加，在到达峰值点后较平缓下降，进入屈曲失稳阶段。L40 的非线性屈曲模式见图9，为柱形壳体两端端部外侧出现环形鼓曲，而试件L40_1在试验时一端出现了鼓曲。由于没有出现破坏阶段，所以平衡路径末端的后屈曲模式保持在鼓曲的变形。

比较图9的数值分析曲线和试验所得的曲线，可以发现二者上升时的斜率存在偏差，从而导致临界载荷对应的位移出现了较大的偏差，图9 中Abaqus 分析所得上升曲线斜率ka=72 035，试验曲线从原点到最高点的直线斜率ke=36 441，试验的上升曲线中间部分斜率（位移0.15 至0.55 阶段）ke=57 382，其中ke/ka=79.66%。Ifayefunmi[9]将其归因于数值分析时边界条件的设置。本文中，试件在端部存在的长度缺陷进一步加大了二者斜率及其位移的偏差。

至此，由试验和非线性屈曲分析可以得出，柱形壳屈服的参考载荷，亦即式（2）得出的理论值Fr更符合试验值和数值分析值。而柱形壳经典弹性临界屈曲载荷Fc适用于厚径比t/R 更小的柱形壳，此时柱形壳由塑性屈曲向弹塑性和弹性屈曲过渡。

根据表3和表4，只对比临界载荷值，对无初始缺陷柱形壳进行非线性分析所得的临界载荷数值，与对有端部长度缺陷的柱形壳进行轴压试验所得的临界载荷很相近。这说明对于塑性屈曲来讲，柱形壳在轴压时对端部的长度缺陷不敏感，即该缺陷对临界载荷值的影响很小，试验中缺陷对临界载荷的影响最高只降低了2.7%。而Błachut[7]得出柱形壳端部缺陷对载荷的影响更大的结论是建立在柱形壳165≤R/t≤1 000，轴压时发生弹性屈曲的基础上。

然而，如表3所示，试验所得的具有最低临界载荷值的三个试件分别为L30_1、L20_1和L20_2，同时这三个试件的△L 也最大，即具有最大的长度缺陷。可以看出端部缺陷对临界载荷确实存在影响，且缺陷越大，临界载荷越小。根据图5 可以看出，缺陷对临界载荷的影响最初体现在轴压初期，其轴向载荷曲线发生了变化。但是总体来看，对于发生塑性屈曲的柱形壳，在正常制造中产生的随机且较小的端部长度缺陷对轴压临界载荷影响很小。

根据表4，可以看出高径比不大于1时，柱形壳的临界屈曲载荷与柱形壳长度无关，此事实通过理论公式也可明显看出。通过数值分析也发现，高度对临界载荷几乎没有影响。但是高度会改变屈曲形状，高度越小时，柱形壳在轴压试验时越有可能在两端产生鼓曲形变。

表4 数值分析、试验及理论所得临界屈曲载荷Tab.4 Critical buckling loads of numerical,experimental and theoretical results

图9 计算和测量得到的位移-载荷图（L40模型）Fig.9 Calculated and measured load-compresion extension relationship of L40 specimens

3 结 论

（1）通过比较柱形壳经典弹性临界屈曲载荷、柱形壳屈服的参考屈曲载荷、数值分析临界载荷和试验得到的临界载荷，可以知道厚径比在低于0.05（厚壳、薄壳分界线）时，柱形壳仍有可能失效在塑性变形区间，产生塑性屈曲。

（2）通过探究不同高度，高径比不大于1的圆柱壳在两端未约束的情况下受轴向压力压缩的屈曲行为，高度对临界载荷值的影响较小。

（3）端部长度缺陷在轴压过程中会导致不规则的形变，且会削弱柱壳初期的轴向承载力，从而体现在降低临界载荷值上。但是通过对比数值分析临界载荷和试验得到的临界载荷，发现端部由于正常制造而产生随机且较小的长度缺陷时（本文长度最大值、最小值的差值与对应柱形壳长度均值的比值最大为0.026），对于可视为相对较厚，且发生塑性屈曲的柱形壳，该缺陷对临界载荷值的影响仍可认为很小。

（4）本文仅研究了端部存在缺陷、高径比较小且为薄壁柱形壳等特殊情况。考虑其他条件，比如其他初始缺陷、更大的高径比等情况的轴向压缩载荷的研究仍需进一步展开。