基于冲蚀-动网格耦合的绕丝筛管冲蚀过程数值模拟

孙岩 楼一珊 曹砚峰 文敏 翟晓鹏 赵轩康

1.长江大学石油工程学院；2.中海油研究总院有限责任公司

绕丝筛管是一种重要的机械防砂工具。绕丝筛管在防砂过程中，挡砂介质受地层砂连续不均匀的冲击，壁面从点痕出现到冲蚀痕迹深度增加，并最终造成绕丝筛管破损的过程被称为绕丝筛管的冲蚀进化(Evolution of the surface profile)［1］。筛管的冲蚀破坏将使防砂失效、油气井大量出砂，导致油气井减产、停产。因此，研究防砂筛管的冲蚀现象将对油气井防砂及筛管设计具有重要指导意义。

为研究防砂筛管的冲蚀磨损现象，Mckeon等［2］通过实验研究了绕丝与基管间距大小对绕丝筛管冲蚀磨损程度的影响；Gilledpie等［3］对不同类型筛管进行冲蚀分析并建立了寿命预测模型；刘永红等［4］通过实验讨论了流速、砂粒直径、砂粒浓度及冲蚀角对割缝筛管冲蚀磨损率的影响；刘新峰等［5］通过研究各因素不同类型筛管的冲蚀影响程度对如何延长筛管使用寿命提出建议；李效波等［6］通过SEM、EDS对筛管冲蚀腐蚀的形貌进行了宏微观分析，根据实验结果对迭加机理进行验证；廖华林等［7］通过实验建立了考虑堵塞问题的砾石充填筛管防砂装置并分析筛管失效原因及堵塞的内在机制。部分学者通过数值模拟手段进一步研究了绕丝筛管的冲蚀破坏问题。Deng等［8］通过流场计算及侵蚀模型的引入研究不同生产压差与含砂量对筛网的侵蚀情况；邓自强［9］采用Fluent软件对割缝筛管进行了液固两相流数值模拟，探究筛管割缝处最大冲蚀率与流速、砂粒浓度和含砂水平之间的关系。目前，数值模拟方法主要用于计算平均冲蚀率以研究冲蚀破坏现象，然而，筛网的破坏主要是筛网受砂砾作用而变形所致。目前研究未考虑到筛网在冲蚀过程中的变形问题。

建立了筛管井下工况的固-液两相流模型，并结合冲蚀动网格耦合方法，在考虑筛管受固体颗粒冲蚀变形、筛管内部过流流量变化的情况下研究绕丝筛管冲蚀进化过程。

1 计算理论

为解决绕丝筛管冲蚀破坏问题，需要解决以下几方面问题，得到不同参数对绕丝筛管筛网变化的影响规律：(1)模型基本理论；(2)有限元模型；(3)模型计算条件和边界条件；(4)模型计算设定参数。

1.1 冲蚀-动网格耦合理论

在实际工况下，设备材料因受冲蚀作用导致质量损失引起几何变形，观测到冲蚀率随时间变化，导致固体颗粒撞击速度发生变化，从而加速或减缓冲蚀的过程，这将影响颗粒流动和冲蚀过程并最终导致材料失效。冲蚀率本质上是瞬态的，因为在绕丝筛管发生质量损失后，流动边界条件发生了变化，然而目前的计算模型仅提供一个初始侵蚀速率，这就使得试验结果有显著的误差。因此笔者利用ANSYS Fluent中基于准稳态方法运行的冲蚀—动网格模型来研究绕丝筛管冲蚀进化的过程。该模型在冲蚀过程的每一段时间间隔捕获因冲蚀作用导致的材料表面几何变形的冲蚀质量损失。并通过该方法重新划分网格,网格位置由动态网格子模型使用物理时间步长更新，并计算该区域的局部流动条件，预测每一时间段的冲蚀率，实现了流-固-冲蚀相互作用的完全耦合［10］。

冲蚀动网格耦合，单个面的网格变形计算如式(1)［10］

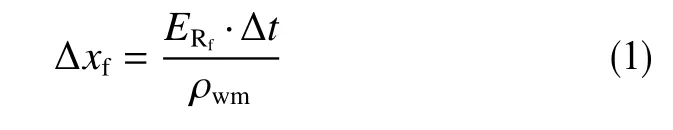
式中，ERf为单位时间内单位面积的侵蚀率，kg · (m2· s)-1；Δt为网格更新的时间步长，s；ρwm为每单位体积质量的设备材料密度，kg · m-3；Δxf为单个面网格变形量，m。

1.2 冲蚀模型

对筛管壁面冲蚀速率采用McLaury模型来计算，该模型主要被用来预测含砂流体对材料壁面的冲蚀磨损［11-13］，形式如式(2)

式中，E为表面磨损率，kg/(m2· s)；V为颗粒速度，m/s；A、k为经验系数，A=F · HBk；HB为材料布氏硬度，N/mm2；F为经验常数；γ为颗粒与壁面冲击角度，°。

冲击角函数可用分段多项式表达

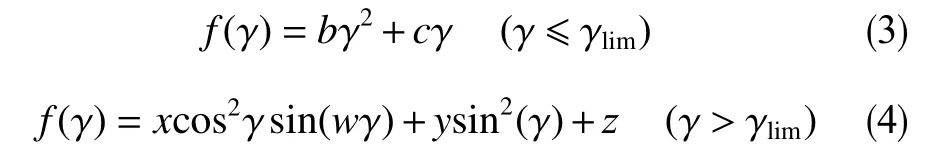
式中，γlim为过度角，15°；b,c,x,y,z,w为经验系数。

1.3 筛管模型

绕丝筛管由基管(带孔中心管)、纵筋和不锈钢绕丝组成。不锈钢绕丝保持一定缝隙缠绕在纵筋上，形成绕丝缝隙。绕丝缝隙在绕丝筛管中起到挡砂作用，绕丝缝隙的宽度可以决定绕丝筛管的挡砂精度。含砂流体穿过绕丝缝隙，通过基管上具有一定密度和孔径的圆孔(基管孔)流入井筒内(图1)。

图1 绕丝筛管模型Fig.1 Model of wire wrapped screen

以Mckeon等［2］试验条件为基础，(表1)建立了绕丝筛管CFD流体域几何模型，如图2所示。设置出口、入口为边界条件，模型参数：绕丝间缝宽0.371 mm；绕丝尺寸2.286×2.667 mm；基孔直径9.525 mm；纵筋尺寸2.286×2.667 mm；纵筋间距9.525 mm；入口截面积0.004 558 1 m2。

在计算域用ANSYS Meshing进行网格划分，采用对复杂几何结构有很强适应性的非结构性网格，对几何模型进行网格独立性验证，不同网格节点数下最大速度大小如图3所示，由图3可知当网格节点数达到350 000时，最大速度基本不变，最终网格划分结果如图4所示；划分了节点数为389 632，单元数为1 993 663个的非结构化网格，网格质量SkewnessMax=0.81，网格质量较好，满足计算要求。

1.4 边界条件及数值计算方法

湍流模型采用Realizablek-ε模型，离散相模型入口面为射流源，入口边界条件设置为速度入口，出口边界条件采用outflow，壁面为无滑移壁面，采用连续相模型和离散相模型(Simple算法)［14］求解。动量、湍流能与湍流耗散率均采用二阶迎风差分格式离散。冲蚀-动网格耦合设置平滑步为5，最大节点移动比例设置为20%，采用可变时间步法设置初始时间步长为10，每个流动迭代次数设置为700步。根据Mckeon等［2］试验给出的试验条件及数据设置入口速度为0.664 m/s、粒径为0.24 mm、砂粒质量流量为0.016 3 kg/s、砂粒密度为2 300 kg/m3、含砂浓度为4.5×103m3、入口流量为3.359 6×10-3m3/s、水力直径为0.071 m，流体相为液态水。

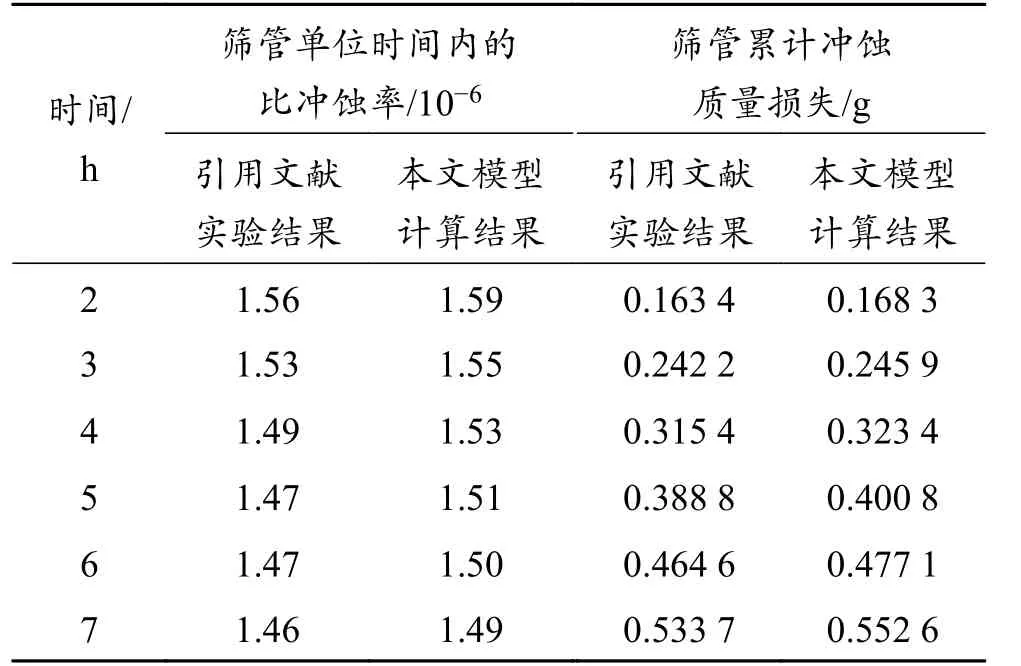
表1 筛管单位时间内的比冲蚀率与冲蚀质量损失计算结果Table 1 Calculation results of specific erosion rate and erosion mass loss of screen per unit time

图2 流体域几何模型Fig.2 Geometric model of fluid domain

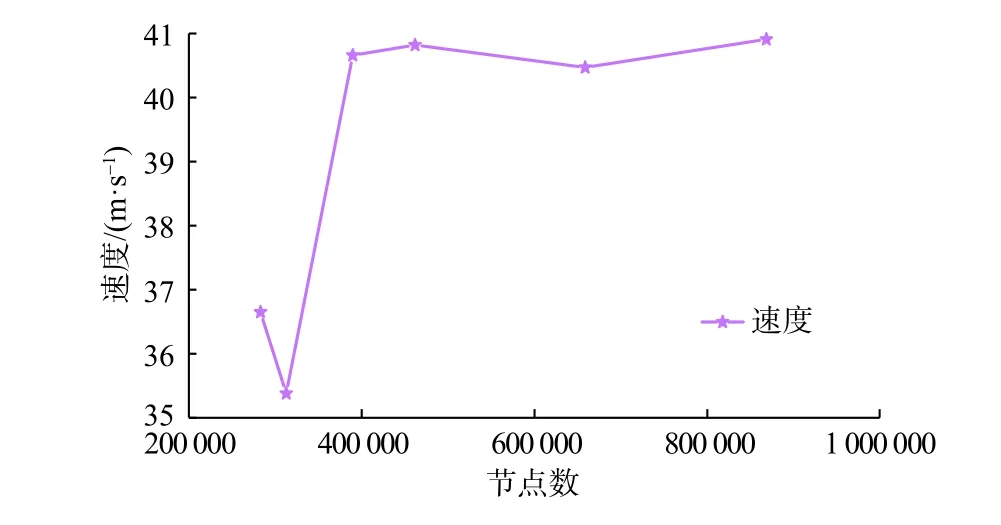
图3 壁面剪切应力随节点数变化曲线Fig.3 Variation of wall shear stress with the number of nodes

图4 网格划分结果Fig.4 Grid division result

2 CFD模型验证

通过CFD后处理模块得到绕丝筛管冲蚀率分布云图，可看出冲蚀磨损严重区域主要集中在基管孔周围，以及绕丝交于纵筋且靠近基管孔一侧区域，将数值模拟结果与实验结果进行比较(图5)可知数值模拟结果较为准确地预测了绕丝筛管发生冲蚀磨损的区域。通过函数计算计算出筛管的比冲蚀率，结果表明单位时间内冲蚀造成的质量损失整体趋势下降，与Mckeon等［2］实验结果对比，整体趋势基本一致(图6)。

图5 绕丝及纵筋实验结果与数值模拟结果对比Fig.5 Comparison between experimental results of numerical simulation results of wrapping wire and vertical member

图6 计算结果与实验结果对比Fig.6 Comparison between calculation results and experimental results

数值计算结果与实验计算的比冲蚀率结果较为相近(表1)，经计算平均误差为1.976%,冲蚀质量损失的结果平均误差为2.73%，单位时间内绕丝筛管的冲蚀质量损失均在0.07 g左右，计算值与实验值接近，进一步佐证了该模型的可靠性。因未考虑到冲蚀进化现象而导致计算结果误差较大的问题在引用冲蚀-动网格耦合计算后得到了有效的解决。

数值计算与实验结果误差原因：数值模拟时未考虑砂粒间相互作用，计算结果较大；由于实际砂粒间存在相互作用致使砂粒能量消耗，降低了砂粒动能，速度随之衰减，因此实际比冲蚀率较低。

3 绕丝筛管动网格冲蚀进化过程分析

3.1 流场随冲蚀时间变化规律

如图7所示，流体流经绕丝筛管后压力逐渐降低；随时间延长进口压力不变，出口压力增大。经CFD后处理函数计算压差可知随冲蚀时间延长，携砂流体流经筛管后压差逐渐降低，主要原因是绕丝筛管逐渐发生冲蚀破坏，节流效应下降，压力向下扩展。

图7 不同冲蚀时间下流场截面压力分布云图Fig.7 Cloud chart of pressure distribution on flow field section at different erosion time

过流流速最高的位置出现在基管孔内及绕丝纵筋靠近基管孔的两侧(图8)，主要原因是携砂流体流经绕丝缝隙，受节流效应，使过流流速增加，通过基管孔再次节流增速喷射入井筒内。随时间的延长，绕丝筛管壁面区域流场流速变化不大。经CFD后处理函数计算流速，由计算结果可知，区域流速随时间延长整体呈下降趋势。这是由于绕丝筛管受冲蚀破坏，节流效应下降，区域整体流速逐渐降低。

图8 不同冲蚀时间下流场截面流速分布云图Fig.8 Cloud chart of flow velocity distribution on flow field section at different erosion time

3.2 绕丝筛管冲蚀随时间变化规律

绕丝筛管冲蚀变形量如图9云图所示。

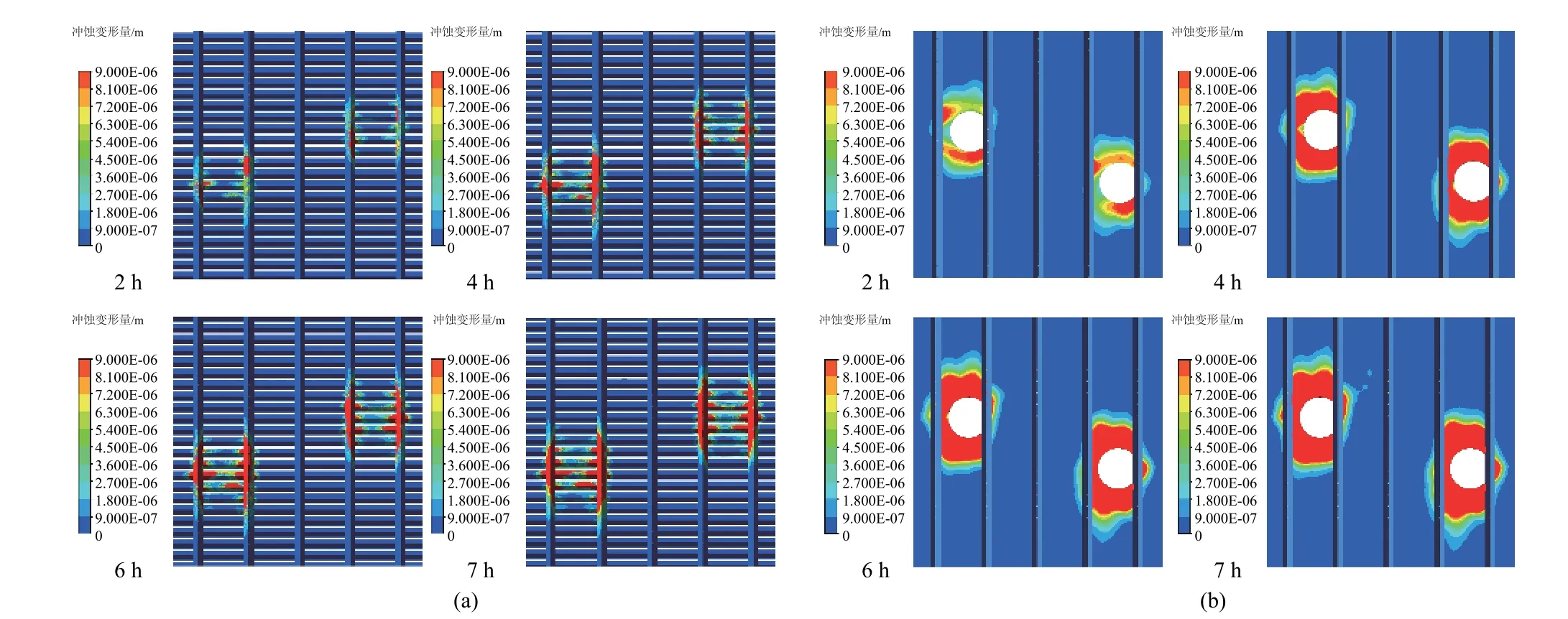
图9 绕丝筛管冲蚀变形量云图(a: 绕丝、纵筋壁面；b: 基管入口端面)Fig.9 Cloud chart of erosion deformation of wire wrapped screen (a: wall surface of wrapping wire and vertical member; b: end face of base pipe inlet)

图9云图中红色区域为发生明显冲蚀变形的区域，主要集中在绕丝下游一侧、绕丝正上方与基管孔周围，更直观地展示了绕丝筛管冲蚀破坏开始于何处。随时间延长，携砂流体不断的冲刷筛管，导致绕丝筛管冲蚀变形量不断增加，冲蚀变形区域逐渐扩大。

携砂流体以0.664 m/s的初始流速流入筛管，绕丝筛管冲蚀进化过程中单位时间内的累计冲蚀变形量及过流流速变化趋势如图10所示。筛管内过流流速平均增量为7.83 m/s，随时间延长，绕丝筛管冲蚀变形量增加，绕丝筛管内过流流速呈递减趋势下降1%左右。这可能是由于绕丝筛管在携砂流体集中流动区域被冲蚀破坏，导致携砂流体流动面积扩大，比冲蚀率降低，从而导致过流流速下降。

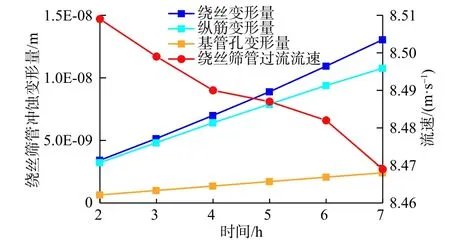
图10 绕丝筛管冲蚀变形量与流速趋势图Fig.10 Trend map of erosion deformation and flow velocity

由图10可看出，绕丝累计冲蚀变形量最多，随时间延长累计冲蚀变形量由3.40×10-9m增长至1.30×10-8m，纵筋累计冲蚀变形量由3.21×10-9m增长至1.30×10-8m，而基管孔累计冲蚀变形量相对较少。这是由于绕丝与纵筋相交处形成暂时的封闭空间，携砂流体首先撞击在绕丝壁面，部分砂粒发生一次撞击弹开后再次或多次撞击在绕丝壁面直至从绕丝与纵筋缝隙中流入井筒(图11)，导致其冲蚀破坏较严重。

通过CFD后处理函数计算绕丝筛管撞击砂粒质量流量，计算结果证明绕丝受携砂流体撞击频次最多，单位时间内撞击砂粒质量流量在0.055～0.040 3 kg/s。其次是纵筋，但纵筋单位时间内砂粒撞击质量流量变化较绕丝较大，由绕丝筛管结构可知(图1)，纵筋之间间隔比绕丝间间隔较大，随时间增加，绕丝筛管受冲蚀破坏，导致携砂流体流动区域发生变化，从而使纵筋受撞击频次变化较大。因此，在筛管设计时可结合实际工况模拟分析，设计合理的绕丝、纵筋、基管孔间隔尺寸来延长筛管寿命。

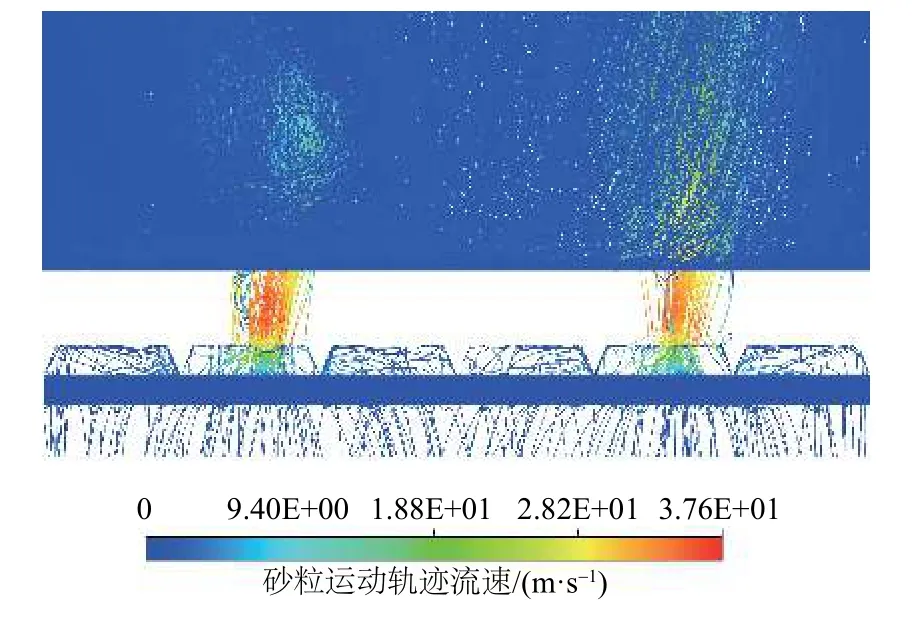
图11 砂粒运动轨迹流速云图Fig.11 Cloud chart of sand trajectory and velocity

采用数值模拟手段考虑了绕丝筛管在冲蚀过程中的变形问题。以上阐述了绕丝累计冲蚀变形量的变化规律，随时间延长可以看出，绕丝及纵筋的几何形状因受冲蚀磨损作用而发生明显变化(图12)，缝隙逐渐变宽。变宽的缝隙在砂粒流动的过程中起到优势通道的作用，节流作用随流动面积增大而减小，导致过流流速下降，如图13所示。

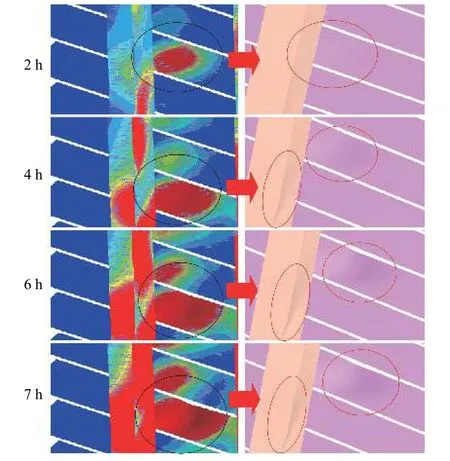
图12 不同时间绕丝纵筋受冲蚀后几何形状变化云图Fig.12 Cloud chart of geometric erosion deformation of wrapping wire and vertical member at different time

绕丝筛管累计冲蚀变形量与冲蚀总质量损失成正比，且均与比冲蚀率成反比，这也证明了绕丝筛管受冲蚀磨损破坏导致流体流动区域增大，挡砂精度变差，从而使得比冲蚀率下降，最终会导致防砂失效。

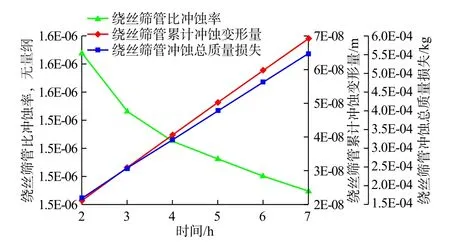
图13 绕丝筛管比冲蚀率与累计冲蚀变形量及冲蚀总质量损失趋势Fig.13 Trend map of specific erosion rate, cumulative erosion deformation and erosion induced total mass loss of wire wrapped screen

4 各因素对绕丝筛管的冲蚀影响

影响绕丝筛管冲蚀率的主要影响因素包括流体流速、含砂质量分数、砂粒粒径、筛管材料性、砂粒硬度等。本文数值模拟研究考虑的主要因素为流速、含砂质量分数、砂粒粒径。Abrams［15］在通过对地层颗粒运移的研究提出1/3桥堵原理，即固相颗粒在地层孔喉处形成“砂桥”的条件是颗粒尺寸为地层孔喉尺寸的1/3［16］。Gillespi等［17］通过实验也得出砂粒直径小于筛网挡砂精度3倍以下时，不存在砂粒堵塞现象的结论。因此，本文在各因素对绕丝筛管冲蚀影响分析的数值模拟研究中不考虑砂粒堵塞情况，采用直径不大于123 μm的砂粒，仅探究细粉砂对绕丝筛管的冲蚀影响。

4.1 流速

冲击角90°、砂粒直径120 μm、含砂质量分数0.5%，入口流速分别取0.664、0.833 2、1.062 4、1.261 6 m/s进行数值模拟计算，绕丝筛管冲蚀率随流速变化曲线及冲蚀分布云图如图14、图15所示。绕丝筛管冲蚀率与携砂流体的流速呈指数关系，这与API中标准的金属材料过流磨损情况相同。随着含砂流体流速增加，砂粒所具有的动能增大，对筛管的冲蚀破坏能力增强。同时，携砂流体流速增加，质量流量随之增加导致单位时间内壁面遭受更多的砂粒撞击，冲蚀率增加，冲蚀质量损失增大。

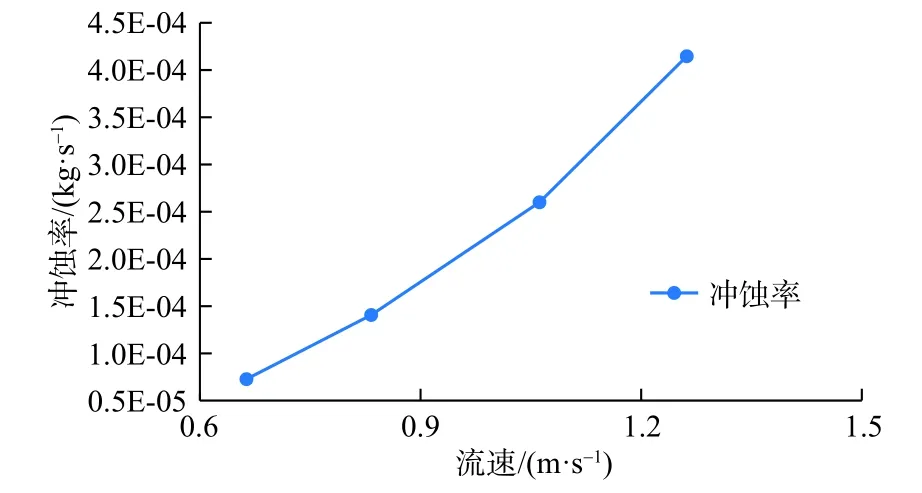
图14 筛网冲蚀率随流速变化曲线Fig.14 Variation of erosion rate with flow velocity

图15 不同流速下筛网冲蚀分布云图(a: 绕丝、纵筋壁面；b: 基管出口端面)Fig.15 Cloud chart of erosion distribution of screen mesh at different flow velocities(a: wall surface of wrapping wire and vertical member; b: end face of base pipe inlet)

4.2 含砂质量分数

冲击角90°、砂粒直径120 μm、流速0.664 m/s，含砂质量分数分别取0.3%、0.5%、0.7%、0.9%进行数值模拟计算，绕丝筛管冲蚀率随含砂质量分数变化曲线及冲蚀分布云图如图16、图17所示。

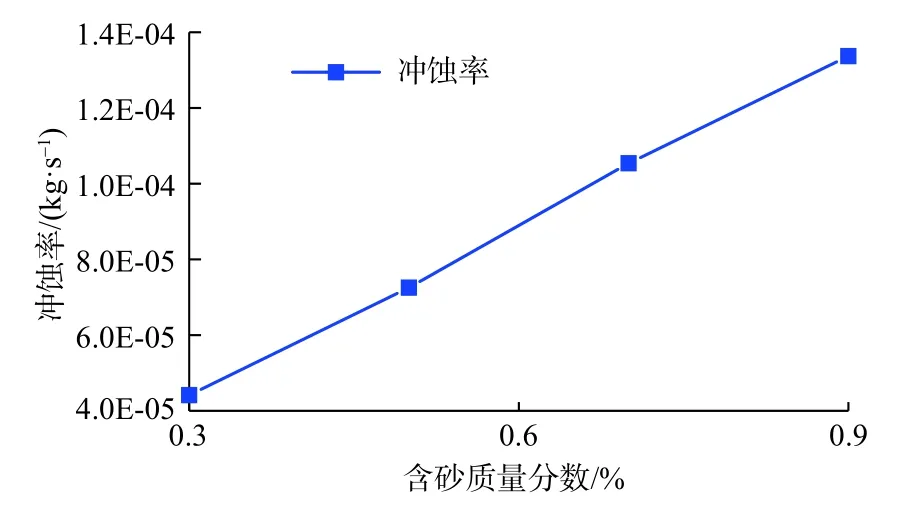
图16 筛网冲蚀率随含砂质量分数变化曲线Fig.16 Variation of erosion rate with sand mass fraction

图17 不同含砂质量分数下筛网冲蚀分布云图(a: 绕丝、纵筋壁面；b: 基管出口端面)Fig.17 Cloud chart of erosion distribution of screen mesh at different sand mass fractions (a: wall surface of wrapping wire and vertical member;b: end face of base pipe inlet)

绕丝筛管冲蚀率与含砂质量分数呈线性关系，绕丝筛管壁面冲蚀破坏区域扩大。原因是增加含砂质量分数即增加砂粒浓度，就代表增加了砂粒与绕丝筛管入口碰撞的次数，单位时间内砂粒撞击筛管壁面的频率增加，导致筛管壁面冲蚀率增加，冲蚀质量损失增加。

4.3 砂粒直径

冲击角90°、含砂质量分数0.5%、流速0.664 m/s，砂粒直径分别取120、100、80、60 μm进行数值模拟计算，绕丝筛管冲蚀率随砂粒直径变化曲线及冲蚀分布云图如图18、图19所示。绕丝筛管冲蚀率与砂粒直径基本呈线性关系，冲蚀破坏区域扩大。原因是携砂流体流速一定，其使砂粒具有的最大动能一定，随砂粒直径增加导致惯性增大，砂粒对绕丝筛管壁面的切削作用增加，从而加剧了绕丝筛管壁面的冲蚀磨损。这一结果符合Misra和Finnie［18］的研究结论之一：材料冲蚀量随砂粒直径的增大而增加。

图18 筛网冲蚀率随砂粒直径变化曲线Fig.18 Variation of erosion rate with sand particle diameter

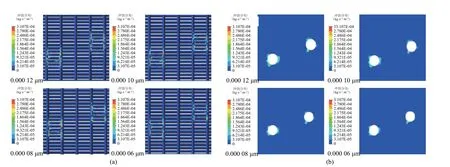
图19 不同砂粒直径条件下筛网冲蚀分布云图(a: 绕丝、纵筋壁面；b: 基管出口端面)Fig.19 Cloud chart of erosion distribution of screen mesh at different sand particle diameters(a: wall surface of wrapping wire and vertical member; b: end face of base pipe inlet)

5 未堵塞工况下冲蚀模型

5.1 冲蚀模型的建立

考虑了流速、含砂质量分数、砂粒直径3个因素，同时考虑筛管材料硬度等，提出一个未堵塞工况下的冲蚀模型

式中，Ev为冲蚀速率，kg/(m2· s)；Vg为筛网过流流速，m/s；Dm为砂粒直径，m；Cp为含砂弄浓度，kg/m3；m为携砂流体质量流量，kg/s；A为筛网面积，m2，本数模面积为0.004 558 1 m2；Δ为冲蚀时间，s；K、a、b、c、d为各参数系数，通过对数模结果进行拟合获得。

5.2 冲蚀模型的拟合

根据不同条件下的数值模拟数据(表2)，运用1stOpt软件对冲蚀模型进行非线性拟合(表3～表4)，优化算法采用麦夸特法(Levenberg-Marquardt)+通用全局优化法。

表2 各方案数值模拟条件Table 2 Numerical simulation conditions of each plan

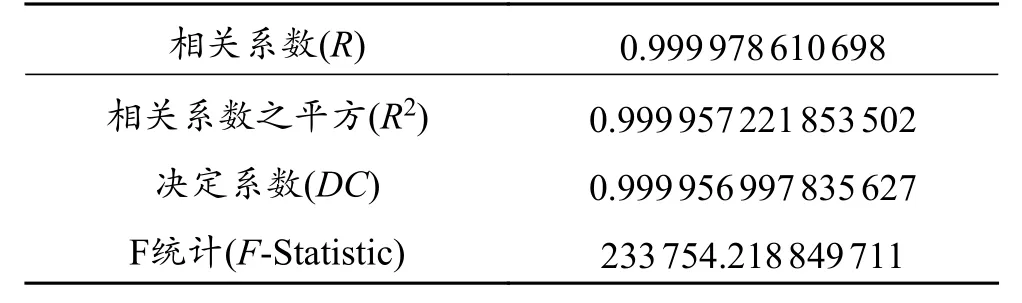
表3 拟合结果相关性Table 3 Correlation of fitting results

表4 各系数拟合值Table 4 Fitting value of each coefficient

拟合结果与数模结果对比如图20所示。最终获得了未堵塞工况下冲蚀模型

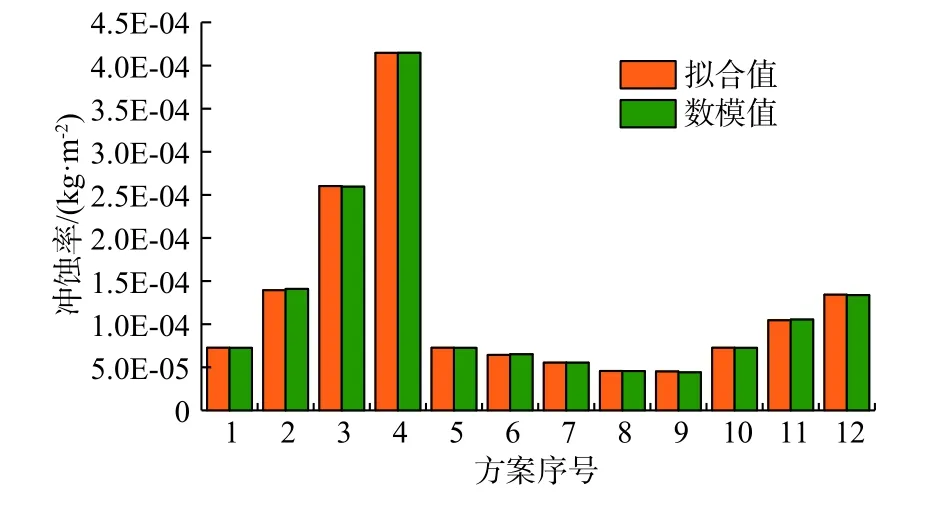
图20 拟合结果与数值模拟数据对比Fig.20 Comparison between fitting results and numerical simulation data

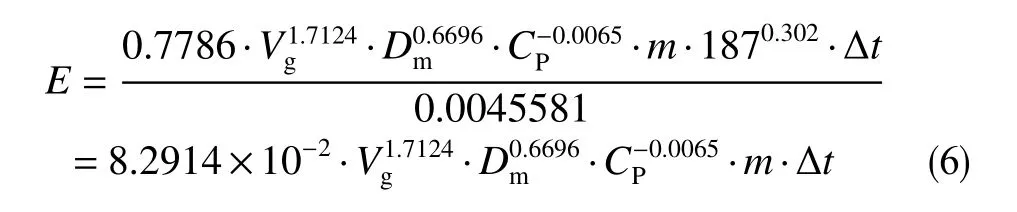
基于上述冲蚀模型，结合Gillespi等［17］通过实验得出当绕丝质量损失约为其质量的2%时，可能会导致防砂失效的结论，在绕丝筛管的使用寿命预测时，将这一条件作为绕丝筛管防砂失效的一临界条件，更准确的预测绕丝筛管使用寿命。

6 结论及展望

(1)研究表明，绕丝筛管冲蚀变形区域主要集中在绕丝下游一侧、绕丝正上方与基管孔周围，直观的表示出绕丝筛管冲蚀破坏开始于何处。随时间增加，由于绕丝筛管在携砂流体集中流动区域不断受到冲蚀破坏，导致携砂流体流动面积扩大，比冲蚀率降低。这对使用冲蚀测试数据来推断井的总寿命或防砂失效时间具有重要参考意义。

(2)数值模拟结果表明，采用冲蚀-动网格耦合模型，在筛网发生冲蚀变形后再次进行网格划分更好的模拟了实际筛网的冲蚀进化现象，较准确的预测绕丝筛管受携砂流体冲蚀筛管表面所造成的的几何变形及失效破坏现象，因此使用此数值手段模拟结果对绕丝筛管的寿命预测及结构设计有着重要参考意义。

(3)在不考虑砂粒堵塞工况(粒径小于123 μm)下，绕丝筛管冲蚀率随流体流速增加呈指数增长，随含砂质量分数及砂粒直径的增加呈线性增长，冲蚀磨损区域扩展现象显著。

(4)由于实际工况较为复杂，涉及因素较多，难以用一个公式或多个公式来精确的描述，因此试验和数值模拟都存在一定的误差，但采用冲蚀-动网格耦合技术进行的数模研究结果误差较小，通过对其数模结果拟合，建立冲蚀预测模型来计算冲蚀率在一定意义上是可取的。