水位变动条件下二元结构岸坡稳定性分析——以扬中市指南村崩岸段岸坡为例

顾 轩,姜月华,杨国强,金 阳,梅世嘉,张 鸿

(1.中国地质科学院,北京 100037;2.中国地质调查局南京地质调查中心,江苏 南京 210016)

河流崩岸是江河岸坡失稳破坏的主要表现形式,又称河岸崩塌、河岸侵蚀、塌岸,是指由土石等物质组成的河岸受到水流冲刷后,在水力、重力、孔隙水压力等作用下失去稳定并沿河、湖的岸坡产生崩落、崩塌和滑坡的现象[1]。这种现象几乎存在于世界上所有的天然江河沿岸,如历史上美国密西西比河下游、欧洲莱茵河都发生过多次崩岸,我国七大江河也普遍存在崩岸现象,以长江中下游河段最为典型[2]。1998 年洪水期,长江崩岸险情发生327 起,长江中下游3 822 km的干堤中,外滩崩岸长度达1 520 km,占沿江总长度的41%[3]。20世纪以来,长江流域兴建各种水利工程,在一定程度上改变了长江的水、沙动态,对下游河道的水文条件产生了较大影响[4]。尤其长江三峡水库建成以来,水库的巨大储存流量改变了下游的水量和流量,拦截了下游的泥沙输送,导致下游水沙条件发生明显变化,清水下泄,下游河床遭到切割,河岸受到侵蚀,崩岸现象频繁发生[5-7]。

目前,国内外对河流崩岸的研究主要着眼于外部水流对河岸的冲刷侵蚀作用,较少关注地下水渗流对河道稳定性的影响[8]。一些学者[9-10]将崩岸分为水流作用(即河岸的侧向侵蚀)及岸坡土体稳定性变化进行研究,DARBY S E等[11]研究了不同土体对河岸稳定性的影响,并在前人研究的基础上对土体孔隙水重量与静水压力对稳定性影响进行了研究。毛昶熙等[12]提出地下水对崩岸的影响并不亚于河水顶冲。王家云等[13]、王永[14]认为长江安徽河段崩岸主要影响因素是水流的冲刷作用,其次是河岸地质条件及高低水位突变产生的外渗压力。张幸农等[15]对于长江中下游的崩岸进行了分类。王延贵[16]建立了河流岸滩崩塌影响因子的层次结构模型,利用层次分析法给出了枯水期和洪水期各主要影响因素的权重系数。宗全利等[17]采用BSTEM模型对二元结构河岸的崩塌过程进行了模拟。随着崩岸研究手段的发展有限元、离散元、有限差分法等数值分析方法已成为分析岸坡稳定性的重要工具[18-22]。

本文以江苏省扬中市指南村崩岸段的岸坡为研究对象,基于非饱和土渗流理论和非饱和土抗剪强度理论,利用GeoStudio软件开展水位变动条件下非饱和土岸坡稳定性数值分析,为河流崩岸机理研究及崩岸治理提供参考资料。

1 指南村崩岸段岸坡基本特征

长江镇江—泰州段位于长江下游扬中河段,属于弯曲分汊河型,是长江中下游河床演变最剧烈的河段之一。特殊的地理位置和地质环境导致该河段发生了一系列岸坡失稳崩塌现象[23]。根据实地调查,1998年以来,镇江市征润洲、江心洲、三茅镇等段均发生了不同程度的岸坡崩塌。本文研究岸坡位于江苏省镇江市三茅街道指南村泰州大桥上游约1.5 km处(图1)。该岸坡于2017年11月8日岸坡失稳发生崩塌,岸线崩塌长540 m,最大进深190 m,面积9.733 km2,造成9户房屋及1座江堤涵洞坍失,是长江中下游近年来发生的较大的一次岸坡崩塌[24]。

图1 指南村崩岸示意图

2 计算理论

2.1 饱和-非饱和土渗流理论

达西定律不仅适用于饱和土渗流计算,还能描述非饱和土中水的流动现象[25-27]。土体渗透满足达西定律条件时,以总水头为变量的二维非饱和渗流运动的基本微分方程为

(1)

式中：H为总水头，m；Q为降雨量(不考虑降雨入渗取值为0)，m3/d；kx和ky分别为水平和竖直方向的渗透系数，m/d；t为时间，d；θ为土体的体积含水率。

公式(1)中∂θ可表示为

∂θ=mw∂uw=mwγw∂hw，

(2)

式中：mw为土-水特征曲线在某一孔压处的斜率；hw为渗流水头，m；γw为水的重度，N/m3。

定解条件包括初始条件和边界条件。初始水头条件为

H(x,y,0)=H0(x,y,0)，

(3)

变水头边界条件为

H|Γ1=H0(x,y,t)-Vt,t≥0，

(4)

流量边界条件为

q(x,y,t)，t≥0,

(5)

式中：Γ1为水头，m；Γ2为流量边界；p为边界Γ2的外法向量。

2.2 非饱和土抗剪强度理论

土质岸坡主要破坏模式是受剪破坏，稳定性主要决定于抗剪强度参数。饱和土的抗剪强度参数可利用摩尔-库仑破坏准则和有效应力概念表达。对于非饱和土而言，有多种抗剪强度理论和公式，考虑本文利用极限平衡法分析边坡稳定性，故选取以正应力和吸力做为变量的非饱和土抗剪强度公式[28-32]

τ′=c′+(σf-us)ftanφ′+(ua-uw)tanφb，

(6)

式中：τ′为土的抗剪强度，MPa；c′为土的有效黏聚力，kPa；(σf-us)f为有效法向应力，N；φ′为土的有效内摩擦角，°；(ua-uw)基质吸力，MPa；φb为抗剪强度随基质吸力而增加的速率。

2.3 边坡稳定性理论

稳定性分析基于极限平衡法中的Morgenstern-Price法。Morgenstern-Price法是一种以水土混合体为研究对象,考虑土条之间的相互作用力,对滑动面的形状、静力平衡、多余未知数的选定等都不作要求的分析方法[33-35]。不仅考虑了条间正应力,还考虑了条间剪应力,且同时能满足力平衡和力矩平衡,与其他极限平衡方法相比更接近于实际情况。假定安全系数并通过迭代求得相应滑动面的安全系数。力矩平衡的安全系数方程为

(7)

力平衡安全系数方程为

(8)

N=

(9)

式中：c为土体黏聚力，kPa；φ为内摩擦角，°；ΔL为各土条在滑动面上的长度，m；LW为各土条到滑动面圆心的力臂长度，m；LN为各土条在滑动面处的中点到对应法线之间的距离，m；α为各土条切线与水平面夹角，°；R为对圆心取矩力臂长度，m；N为滑动面对土条的法向作用力，N；λ为条间作用力变化系数；f(x)为条间作用力变化函数。

3 计算模型

3.1 土体力学参数

为了分析崩岸河段土体组成与力学特性,对崩岸断面进行实地查勘,并开展工程钻探。根据钻探揭露的土体组成、结构及性质不同,进行分层取样,取样点坐标119°50′56.55″E, 32°14′3.88″N。对采集的样品进行室内土工试验,包括土体颗粒分析、比重、密度、含水率、原状土抗剪强度及渗透试验等,试验结果反映土质类别、组成、渗透性、密实度和抗剪强度等指标(表1)。

表1 土体力学性质参数

指南村崩岸段土体上部为粉质黏土的黏性土体,下部为粉砂等非黏性土,组成的“二元结构”。上部土体从上至下的黏粒含量分别为2.2%、1.4%、2.2%、1.8%,粉粒含量分别为27.3%、11.4%、13.1%、11.2%,砂粒含量分别为70.5%、87.2%、83.9%、87.1%。河床底部物质组成为砂层和砾石层。

3.2 计算模型及边界条件

岸坡为上层粉质黏土与下层粉砂组成的典型二元结构岸坡,且下部粉砂层较厚。根据2015年实测的指南村崩岸段岸坡地形图(图2),选取断面Ⅲ将岸坡形态概化为河底高程-50 m,坡比为1∶6,根据土体性质不同,将崩岸岸坡分为上部粉质黏土和下部粉砂,按照土体力学参数不同将粉砂细分为3组(图3)。

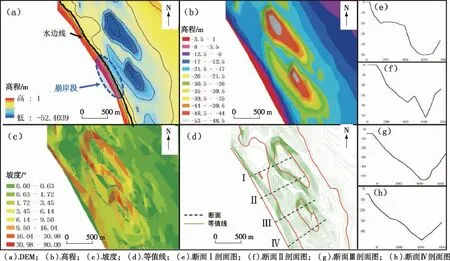
图2 岸坡地形及断面剖面图

图3 计算模型示意图

粉质黏土和粉砂1选用饱和-非饱和模型,其余各土层选用饱和模型,非饱和土体体积含水量函数采用Seep/w自带的黏土含水量函数,渗透系数函数利用Van Genuchten函数拟合,得出其土水特征曲线和渗透系数函。使用软件内嵌网格划分程序自动划分网格,全局单元大概尺寸为1 m,共获得15 081个网格单元,15 469个节点。

3.3 计算工况

根据长江海事局公布的2019年9月—2020年8月镇江段江水水位(图4),设计概化水位工况如下。

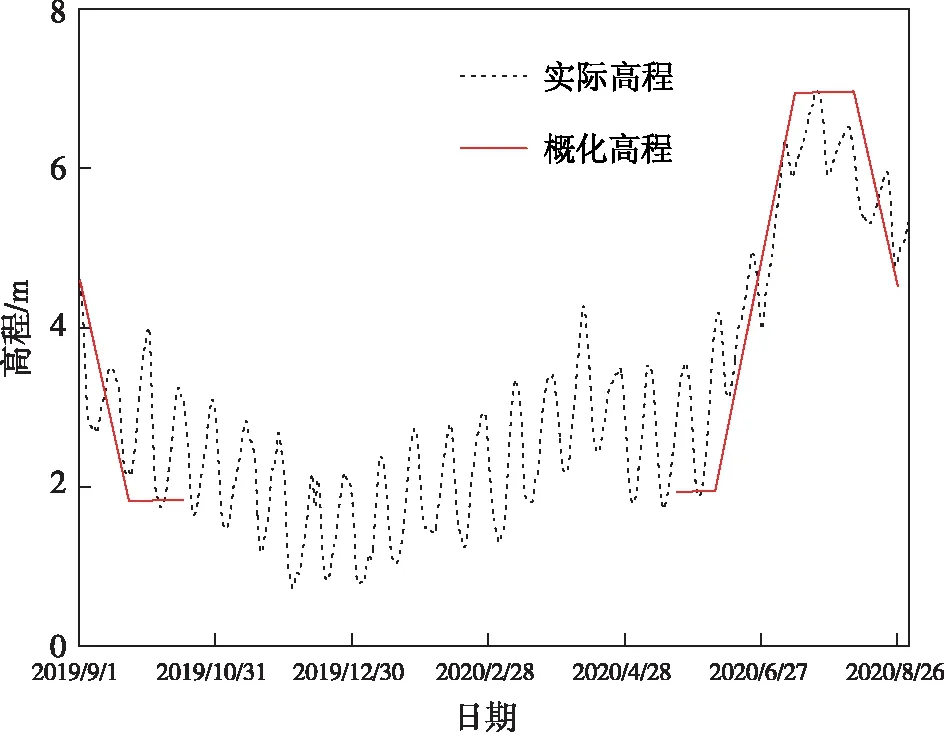
图4 镇江段江水水位变化图

水位上升阶段:水位从0 m上升至5 m,水位上升速度0.25 m/d,持续20天。

水位持续较高阶段:水位维持在5 m,持续25天。

水位下降阶段:水位从5m下降至0 m,水位下降速度0.2 m/d,持续25天。

3.4 模拟结果及分析

3.4.1 安全系数曲线

由Seep/w分析得到各点土的孔隙水压力在涨水期、洪水期和退水期的变化,基于孔隙水压力的变化在Slope/w模块中求解边坡的安全系数(图5)。可见,在上述工况条件下的岸坡安全系数总体上呈现先上升后不变、最后下降的趋势,与水位变化的趋势一致,但时间上略有延迟。

图5 安全系数曲线变化图

3.4.2 结果分析

(1)涨水期(0～20天)。水位上涨过程,岸坡安全系数随水位升高而增大。水位上涨,侧向水压力增加,岸坡内浸润线出现明显起伏变化,呈下凹状,动水压力可抵消一部分坡体的滑动力。水位上升初期,孔隙水压力变化幅度较小(图6),岸坡土体内基质吸力较大(图7)。土体含水率增大速度缓慢,抗剪强度减小的幅度较小(图8)。可见,0～20天内的安全系数总体上呈上升趋势,上升的幅度逐渐减小;在此阶段末期,由于抗剪强度的减小幅度不断增大,基质吸力减小,安全系数略有下降。总体来说,涨水期水位上升阶段的岸坡朝稳定的状态发展。

(2)洪水期(20～45天)。此阶段地表水水位到达最高,侧向水压力对于岸坡的支撑作用达到最大。在此阶段初始几天内,地下水位逐渐趋于稳定,孔隙水压力达到稳定(图6),土体含水率增至最大(位于浸润线下方的达到饱和),土体抗剪强度先持续减小后保持不变(图8)。孔隙水压力达到稳定,基质吸力先变小后保持不变(图7)。所以,安全系数的变化情况为先减小后不变。

(3)退水期(45～70天)。水位下降过程中,侧向水压力最先开始减小直至消失,在渗流作用力的影响下岸坡下部粉砂层可能发生潜蚀,稳定性进一步降低。岸坡土体含水率下降,但相比于涨水前的含水率仍然较大,抗剪强度较低(图8)。在这一阶段,对于岸坡支撑作用极大的侧向水压力消失,基质吸力和抗剪强度仍较低(图6,图7),因此,安全系数呈下降趋势。

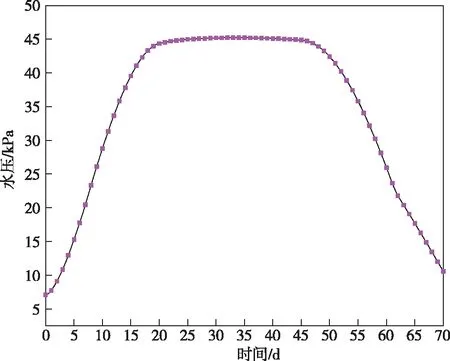
图6 孔隙水压力变化曲线

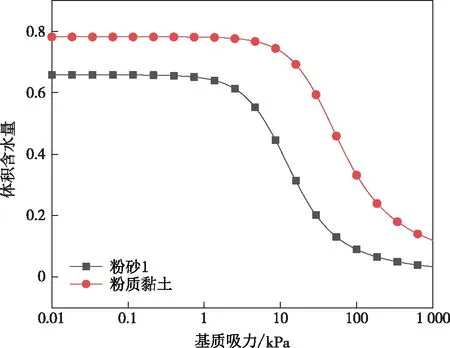
图7 水土特征曲线

图8 土体抗剪强度变化曲线

模拟结束时,安全系数最低值为1.326(图5)。需要说明的是,本次模拟计算仅考虑了水位变化和岸坡土体本身的性质对于岸坡稳定性的影响,并未考虑上部荷载加大(居民住房、人工江堤修建等)和持续降雨对于岸坡稳定性的影响,而这些将增加岸坡破坏坍塌的可能性。因此,若考虑上述因素,岸坡的稳定性比目前计算结果更低,崩岸更易发生。

3.5 水位波动速度对岸坡稳定性的影响

水位波动对于岸坡稳定性的影响较大。通过模拟不同水位涨落速率,尤其是特大水位涨落速率下的渗流场变化对岸坡稳定性的影响,找出不同水位涨落速率和水位涨落条件下岸坡稳定性之间的关系,对崩岸的成因机制的研究具有重要意义。

选取水位从0 m上升到5 m和从5 m下降到0 m两个过程进行模拟,初始渗流场条件分别为0 m和5 m,水位的波动速率分别为0.1 m/d、0.2 m/d、0.25 m/d、0.5 m/d、1 m/d。0.2 m/d较接近江水水位波动的真实速率。

3.5.1 江水水位从0 m上升到5 m

水位选择上升速率分别为0.1 m/d、0.25 m/d、0.5 m/d、1 m/d,相应的稳定性结果如图9所示。

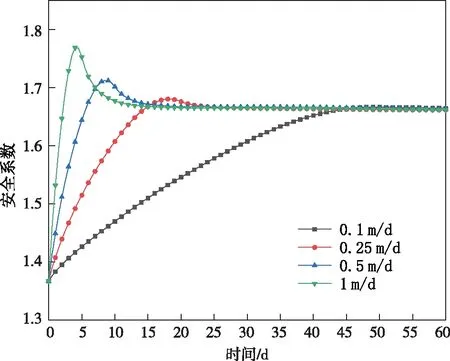
图9 不同水位上升速率下的安全系数

从0 m高程开始,江水水位以不同的上升速率上升的过程中,岸坡的稳定性呈先上升后下降,最后逐渐恢复到稳定状态。当上升速率较大时,达到稳定性最大值之前,动水压力是影响滑坡稳定性的主要因素;随着江水不断渗透,土体的物理力学性质发生变化,岸坡稳定性开始逐渐降低,直至恢复稳定状态;但当上升速率较小时,稳定性随着孔隙水压力、浮力、土体物理力学性质的变化而变化。安全系数随着江水水位上升速率的增大而增大。当江水水位上升速度为1 m/d时,稳定性急剧上升,5天后达到最大值。当江水水位上升速率为0.5 m/d时,稳定性急剧增加,10天后达到最大值,然后缓慢下降,趋势与上升速率为1 m/d时相似。随着江水水位升速度的降低,安全系数的增长速度相对变小。在0.1 m/d、0.25 m/d两种上升速率下达,稳定系数达到最大值时间分别为24 天和52 天。所有上升过程中,岸坡恢复稳定状态的时间约为60天,安全系数比江水水位上升前相对较高,约为0.2。江水水位上升越快,安全系数最大值越大。

3.5.2 江水水位从5 m下降到0 m

水位选择的上升速率分别为0.1 m/d、0.2 m/d、0.5 m/d、1 m/d,相应的稳定性结果如图10所示。

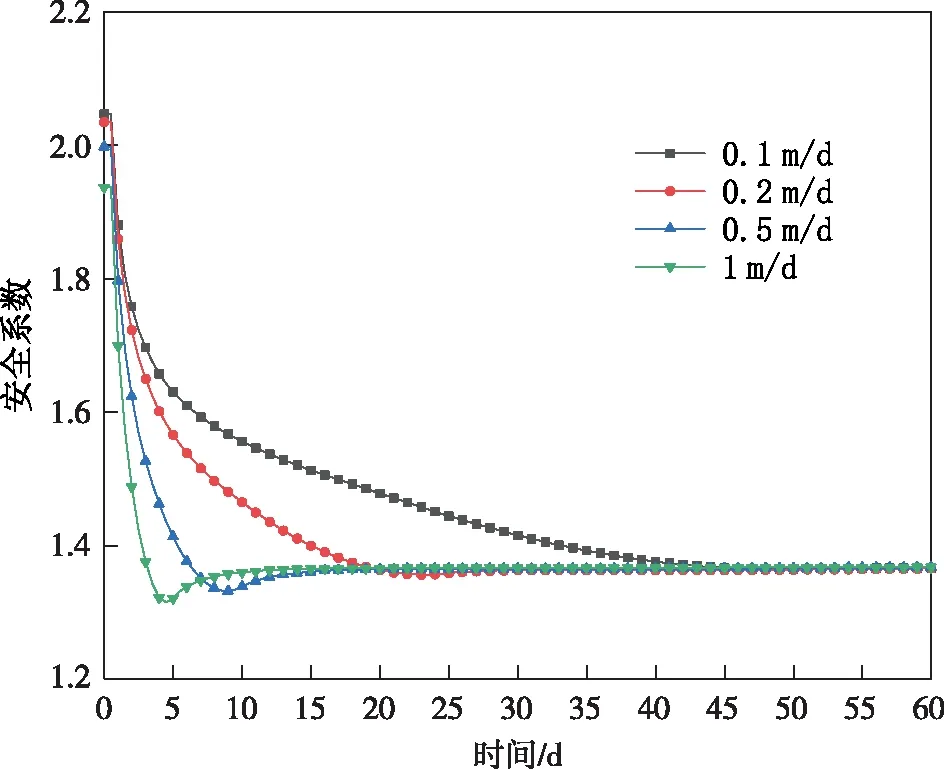
图10 不同水位下降速率下的安全系数

从5 m高程开始,江水水位以不同的下降速率下降的过程中,岸坡稳定性呈先下降后上升,最后逐渐恢复稳定状态。当下降速率较大,稳定性达到最小值之前,动水压力是影响滑坡稳定性的主要因素。稳定达到最小值后,随着地下水不断排出,土体的物理力学性质向稳定方向变化,岸坡稳定性开始逐渐增加,直至最终恢复到稳定状态;下降速度较小时,渗流场变化缓慢,稳定性随孔隙水压力、浮力、物理力学性质的变化而变化。安全系数随江水水位下降速率增大而减小。当水位下降速度为1 m/d时,稳定性开始急剧下降,5天后稳定性达到最低。当水位下降速率为0.5 m/d,稳定性也急剧下降,10天后达到最最低,然后缓慢上升,趋势与下降速率为1 m/d相似。需要注意的是,在水位下降速率为0.5 m/d和1 m/d条件下,安全系数<1.35的天数分别为4天(第7.5天—第11.5天)和3.5天(第3.5天—第7天),所以,在仅考虑水位变动的条件下,水位骤降>0.5 m/d时,岸坡长期处于不稳定状态,易发生失稳崩塌。随着水位下降速率的减小,安全系数的下降速度相对变小。在0.1 m/d、0.2 m/d两种速率下达到稳定的时间分别为30天和55天。所有下降过程中,岸坡恢复到稳定状态的时间约为60天,安全系数比江水位下降前较低。水位下降越慢,安全系数最小值越大。

4 结论

(1)指南村崩岸段岸坡属于“二元结构”,岸坡下部粉砂层较厚,崩岸土体的抗冲刷能力较弱。粉砂层的透水性好于粉质黏土层,为地下水的渗流提供了良好的环境。

(2)江水水位变动引起的饱和—非饱和渗流对于岸坡稳定性有明显影响。模拟结果表明,非饱和土渗流出现于水位变化较大的涨水期和退水期,会改变土体内孔隙水压力的分布情况,导致岸坡的安全系数在涨水期上升,在退水期下降,即在退水期的岸坡稳定性最差,最容易发生岸坡崩塌,这与实际调查的情况相符。

(3)在江水水位上升的过程中,上升速度越快,岸坡安全系数的最大值越大,即岸坡在水位骤涨时更加稳定。初始状态下静水压力是主导因素,水位达到最高后,浮力增大,内聚力和摩擦角逐渐减小,最终岸坡稳定性逐渐降低到稳定状态。

(4)在江水水位下降的过程中,下降速度越快,岸坡安全系数的最小值越小,即岸坡在水位骤降时更加容易发生失稳崩塌。初始状态下动水压力和静水压力是主导因素。但当安全系数达到最小值后,物理力学性质的变化成为主导因素,最终岸坡稳定性逐渐回升到稳定状态。在仅考虑水位变动的条件下,水位骤降速率>0.5 m/d时,岸坡便会长期处于不稳定状态,易发生失稳崩塌。