关于拉普拉斯变换的几个定理

赵成兵，刘丹秀，刘慧慧

(安徽建筑大学数理学院 安徽 合肥 230022)

对于一维的Laplace变换在文献[1-3]中都有详细的介绍，有很多好的性质及其应用，如微分性质、积分性质、卷积等，在文献[4]中介绍了高维的Laplace变换。Laplace变换及其逆变换有着很多的应用，如计算积分以及求解微分方程等，在文献[5-10]中皆有所阐述。本文主要对一维和二维的Laplace变换进行研究，得到它们的功率定理和自相关定理且对二维Laplace变换做了一些工作，得到它的留数定理和微分性质。

对于一维Laplace积分定义如下

其中f(t)是实值函数，s=α+iβ为一复数。

对于一维的Laplace变换有如下的存在定理：

引理1：若函数f(t)在区间[0,+∞)满足下列条件：

(1)f(t)在一有限区间上分段连续；

(2)存在某个常数M>0,c>0使得|f(t)|c上积分

存在，且此积分确定的函数F(s)解析，记为

F(s)=I [f(t)]

定义1：一维的Laplace逆变换定义如下

记为f(t)=I-1[F(s)]

下面我们研究Laplace变换的功率定理和自相关定理，首先我们从一维情况出发得到如下定理。

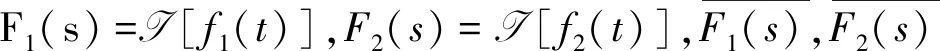
证明：

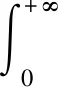
定理2：若F(s)=I [f(t)],则有如下的公式成立

证明：由位移性质知道

I [f(t+τ)]=esτI [f(t)]

由定理1得

=I-1[|F(s)|2]

下面我们介绍二维的Laplace变换及其逆变换并讨论它的一些性质和应用。

定义2：若f(t1,t2)是二维实值函数，在t1≥0,t2≥0,上有定义，且积分

在C2区域上收敛，(s1,s2)∈C2，则称此积分为函数f(t1,t2)二维的Laplace积分。

对于二维的Laplace积分我们可以由引理1得到类似的二维的Laplace变换的存在定理，这里我们不在证明，对于二维的Laplace变换以及逆变化，它们分别记为

F(s1,s2)=I [f(t1,t1)]

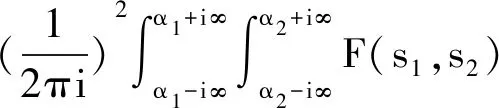
e(s1t1+s2t2)ds1ds2

其中sj=αj+iβj,j=(1,2)。

定理3：若F(s1,s2)在复平面对复变量s1有s11,s12,...,s1n,个奇点，在复平面对复变量s2有s21,s22,…,s2m,个奇点，且sj→∞,F(s1,s2)→0,j=(1,2)，则有如下的公式

证明：选择合适的α使得αi<α,i=(1,2)，则有

I-1[F(s1,s2)]

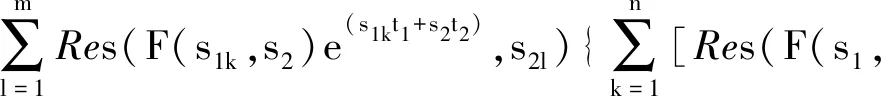
s2)e(s1t1+s2t2),s1k]}

对于二维Laplace变换我们同样可以讨论它的微分和积分性质，由于

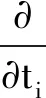
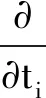
e-(s1t1+s2t2)

i=(1,2)

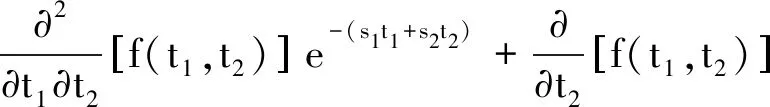
(-s1)e-(s1t1+s2t2)+(s1s2)f(t1,t2)e-(s1t1+s2t2)

所以我们有如下性质

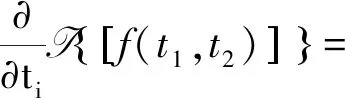
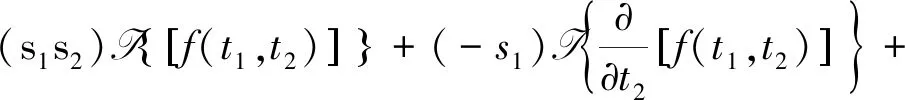
对于它的积分性质我们可以同样类似地得到。下面我们讨论对于二维Laplace变换的功率定理和自相关定理。

定理5：若F(s1,s2)=I [f(t1,t2)],则有如下的公式成立

=I-1[|F(s1,s2)|2]

证明过程类似与定理1和定理2，我们不在重复，对于高维的Laplace变换我们可以得到同样的一些性质定理且它们可以广泛的应用与求解偏微分方程。