有机高聚物中高能载流子自旋极化研究

李 超， 马 果

(南阳理工学院数理学院 河南 南阳 473004)

0 引言

有机发光材料价格低廉，易于处理，并且种类众多，具有良好的机械性能及可塑性，具有广阔的应用前景。1986年，Tang等通过真空储存的ITO/CuPc/PV/Ag双层器件首次实现了有机电致发光[1]，该器件显著的好处就是电荷的产额不受电场大小的影响，因此Tang后来被称为“有机发光二极管(OLED)之父”。2004年，Francis 等人[2]利用高聚物得到了一种单层的有机材料结构, 该材料不含磁性电极，却能在室温条件下，外加10 mT的磁场就能观测到相当可观(大约10%左右)的磁电阻现象，此即非常著名的巨磁电阻效应。自旋电子学就是由巨磁电阻效应所开辟的一个新兴学科，区别于传统电子学只关注电子的荷电性，自旋电子学更多地考虑电子的自旋特性：如何通过外磁场调控电子的自旋性质；如何在电子传导过程应用自旋磁性实现对电子输运性质的调控。

有机非磁性器件的磁电阻效应是目前有机自旋电子学研究的热点，而有机磁电阻效应形成的物理机制尚未清楚，基于有机材料独特的载流子特性，目前存在3种主流的解释：(1)极化子对机制[3]。磁场改变了单态与三重态极化子对间的比率，从而产生磁场效应。(2)激子-极化子淬灭机制[4]。(3)双极化子机制[5]。自旋极化和自旋输运是有机自旋电子学的基础，是目前有机自旋电子学主要的研究方向之一，是自旋极化电子(空穴)的注入、输运与探测的重要研究途径，对进一步理解有机磁电阻效应的物理机制也是极为必要的。本文主要利用一维Su-Schrieffer-Heeger(简称SSH)模型，考虑自旋轨道耦合相互作用，在有机半导体中注入电子到高能级时载流子自旋极化情况，同时还研究了电声耦合相互作用对自旋极化的影响。

1 SSH模型

有机高聚物分子量较大，在整体的分布一般由简单的集团构成。考虑最简单的情况，以聚乙炔为例：它主要由(CH)集团形成的，可视为一维链式结构。体系总的哈密顿量，在自然边界条件下可写作下述形式

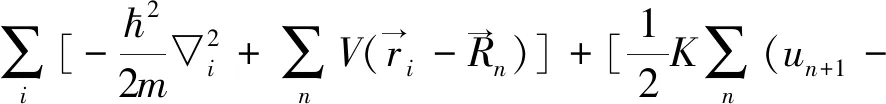
(1)

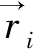
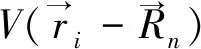
(2)

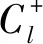
上式中仅包含电子的哈密顿量，将晶格部分的哈密顿量考虑进来以后，系统总的哈密顿量即可写为

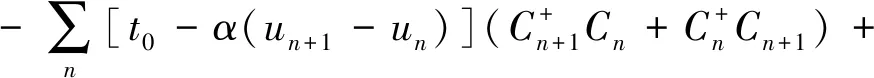
(3)

此即为SSH模型的哈密顿量[6]，该方程被广泛应用于准一维有机共轭高分子聚合物，用于研究它们的各项物理机制，包括光、热、电磁等物理性质及其电荷-自旋特性。

2 内容与方法

基于SSH模型，将电子注入到有机材料中，研究其自旋极化的情况，可以对磁电阻的物理机制进行初步探究。早在2010年，K Tarafder等人[7]利用密度泛函理论对Alq3中注入电子的自旋极化情况进行了计算，结果表明：电荷的注入会使系统产生净磁矩；并且磁矩会随着注入电子的增多呈线性增加的趋势。然而令人疑惑的是系统磁矩的产生远大于电荷的注入量。基于密度泛函理论，D Hou等人以单链聚噻吩为模型研究了系统的自旋极化在0-1e电子注入时的变化[8]，发现了磁矩与注入电荷量的聚合度相关，由此可以认为在有机材料中，自旋极化和电子-电子相互以及电声耦合有关。2014年，S X Han等人[9]基于SSH模型研究了在单链有机聚噻吩分子中注入电子时的自旋极化情况。结果表明，自旋极化与分子的聚合度和注入的电子数量都有关系。研究还发现了自旋极化的产生与载流子的局域性也存在一定的联系。这些研究都仅限于电子注入到LUMO能级时的情况，事实上，有机材料中电子的注入，通常可以使电子占据更高的分子能级，如LUMO+1、LUMO+2等，对于高能级电子注入的情况，需要更进一步进行研究。

基于SSH模型，建立一维聚噻吩的哈密顿量

H=Hel+Hee+Hso+HK=

(4)

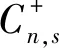
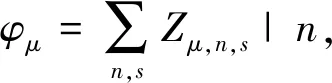
-[t0-α(un-un-1)+(-1)n-1te]Zμ,n-1,s-

[t0-α(un+1-un)(-1)nte]Zμ,n+1,s+

(5)

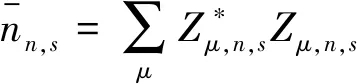
(6)

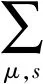
3 结果与讨论

基于上述扩展的SSH模型我们利用fortran语言自洽迭代得到了注入一个电子到有机聚合物中时系统静态下的相关物理量，并根据得到的数据利用Origin软件进行数据分析。

通过分析我们发现，电声耦合相互作用在有机聚合物中表现得极为强烈，当电子被注入到聚合物体系时，电子将诱导晶格产生畸变，从而形成诸如极化子、双极化子之类的束缚态。将电子注入到高能级研究高能载流子的自旋极化，发现电子注入到不同能级，如LUMO、LUMO+1、LUMO+5、LUMO+7时，体系的电荷分布、晶格位形以及自旋分布都随着能级的增高而扩展。如图1所示，将电子注入到不同能级时，系统的局域因子ξ随着载流子的能量的增大而变小，即电子注入LUMO能级时系统的局域性最大；当载流子能量大于0.015 eV左右时，系统的局域因子降到最低，即系统此时呈现扩展态。

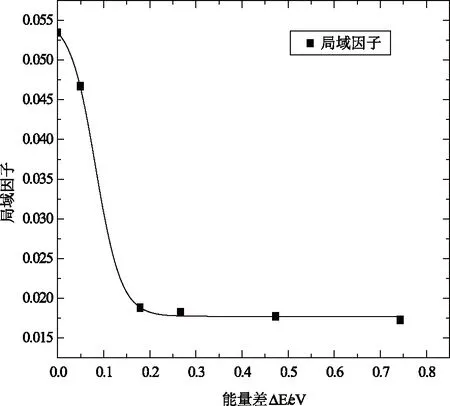
图1 将电子注入到不同能级上时，体系局域因子随载流子能量的变化关系

随着电子向高能级的注入过程，可以发现电子注入的能级越高，体系的磁矩越小，如图2所示，不同形状的数据点分别表示不同取值的自旋轨道耦合参数tso下，体系磁矩的变化。该结果和局域因子随载流子能量的变化趋势相一致，即：当电子注入到较低能级时，载流子可以保持很好的局域性，随着电子向高能级的注入，载流子局域性迅速下降。该结果可根据自旋轨道耦合相互作用的物理图像进行理解：当电子从一个格点跃迁到另一个格点的时候，电子将会发生自旋翻转，每个格点不同自旋的电荷密度趋向于相等，所以不会有自旋极化的出现。研究发现当自旋轨道耦合为零时，注入的电子呈完全自旋极化的状态，如图2最上方黑色实线所示；当自旋轨道耦合逐渐增强时，电子为自旋混合态，但对于电子注入到LUMO能级的情况，自旋轨道耦合对自旋极化几乎没有影响；而对于电子注入高能级的情况，从图2可以看出，当自旋轨道耦合tso≤0.04 eV时，随着载流子能量的增大，自旋极化逐渐变小直至达到饱和，而当tso≥0.06 eV时，自旋极化呈断崖式下跌迅速降为零。

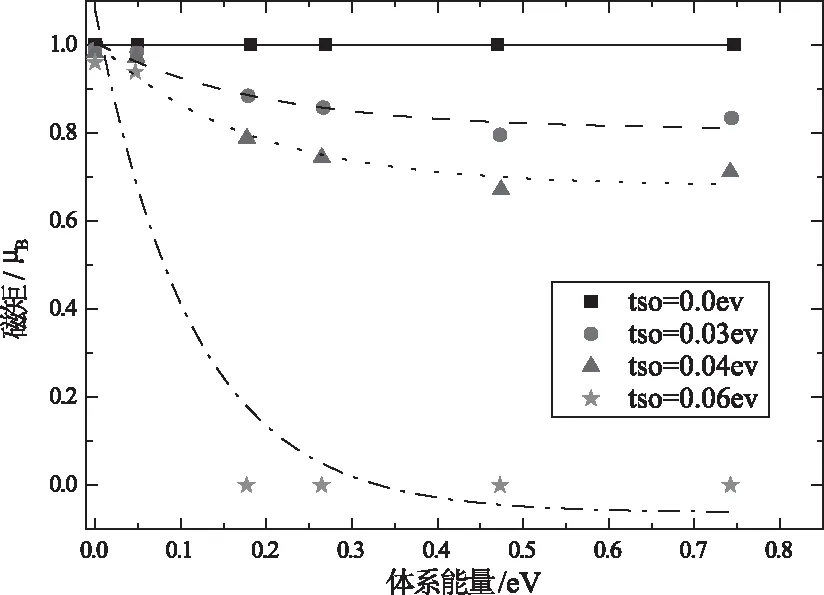
图2 不同tso的情况下，电子注入到不同能级时磁矩的变化

作为有机半导体的重要特性，我们研究了电声耦合相互作用对自旋极化的影响，结果表明：在同一电声耦合参数下，系统的磁矩都是随着自旋轨道耦合参数的增大而减小。而对于同一能级，如图3所示，电子注入到LUMO能级，在不同的自旋轨道耦合参数下，磁矩随电声耦合参数的变化趋势相同。

然而，对于不同的能级，磁矩随电声耦合参数的变化趋势却有可能表现得截然相反，如图4所示，电子注入较低能级(LUMO，LUMO+7)时，磁矩随电声耦合参数的增大而增大；当电子注入较高能级(LUMO+15,LUMO+25)时，磁矩随电声耦合参数的增大而减小。为了深入理解这一现象，我们进一步研究了电子与电子之间的相互作用。电子-电子相互作用源于同一格点处的电子间的库仑排斥，倾向于自旋极化分布，当电子注入高能级时，电子局域会很低，此时的磁矩比电子注入LUMO能级时要小。在一定的电子-电子相互作用下，极化子的自旋极化会随着自旋轨道耦合系数的增大而减小，如图5所示。因此，在高能情况下，磁矩更多的依赖自旋轨道耦合的强弱；而在低能情况下，磁矩则主要受到电子与电子之间相互作用的影响。

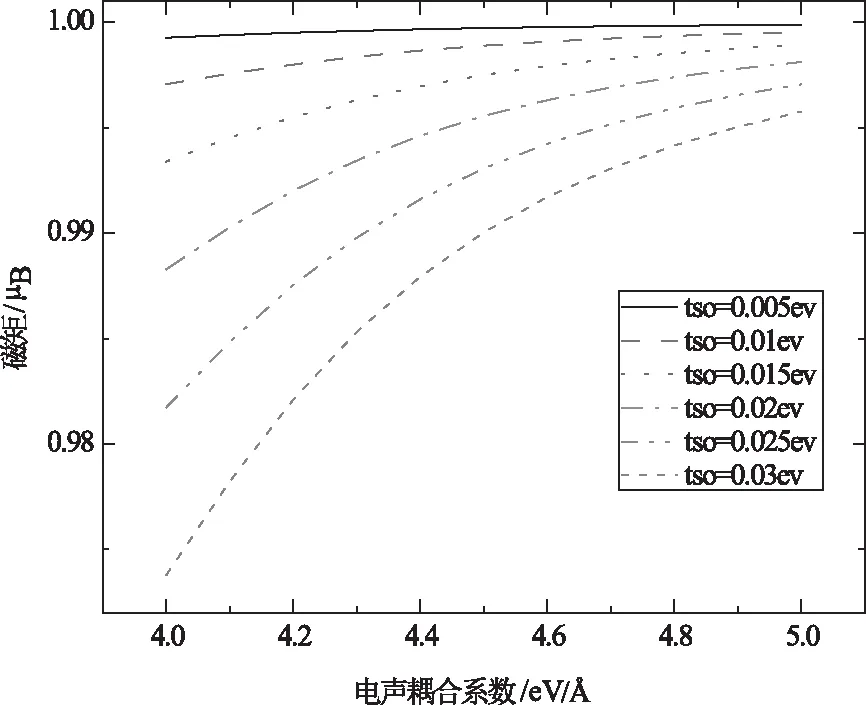
图3 电子注入LUMO能级时，磁矩随电声耦合系数的变化

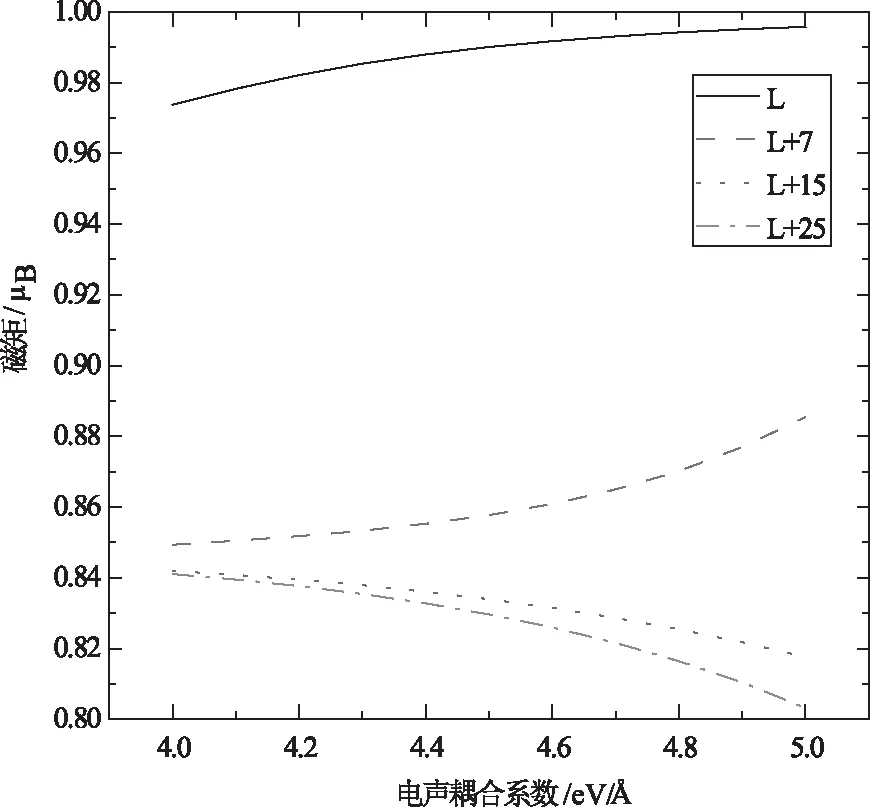
图4 电子注入到更高能级上时，磁矩随电声耦合系数的变化

图5 电子注入到不同能级上时，磁矩随自旋轨道耦合系数的变化

由此一来，图4中的现象就得到很好的解释：当电子注入低能级时，电子的局域性较强，电子与电子之间的相互作用占主导，磁矩随电声耦合参数的变大而变大；当电子注入高能级时，电子的局域性表现为扩展态，则电子与电子之间的相互作用变得极为微弱，此时影响磁矩的主要因素为电声耦合相互作用，即电声耦合越强，磁矩越小。

4 结论

基于一维紧束缚模型，研究了电子注入一维有机聚合物体系时，在不同能级下系统自旋极化的情况。结果表明随着电子注入能量的增大，体系的自旋极化呈下降趋势，这与实验上有机器件磁阻随偏压增大而减小的现象相一致。同时，研究还发现随着偏压的继续增大，电子将会被注入到更高的能级，由此载流子会具有更高的能量，此时高能载流子的能量将和偏压成正相关的关系。另外，电声耦合相互作用对自旋极化的影响也进行了研究，结果表明，在低能级时，电声耦合系数越大，磁矩越大；在高能级时，电声耦合系数的越大，磁矩反而越小。这是因为当电声耦合系数增大的时候，体系的局域性变强，电子与电子之间的相互作用也增强。