创设“真情境”,让学习在学与教的价值归一中走向深刻
——以“三角形”部分的教学为例
文|管小冬
“真情境”是指教师在创设情境、引领学生展开学习活动时,立足学生的生活经验与认知水平,注重情境创设与周围世界相连、与真实生活相通。在儿童教育家李吉林创立的情境教育体系中,“真”是四大核心元素之一。她认为,儿童情境学习的第一步便是“从‘真’出发,由‘真’去追求‘美’,去启迪‘智’,去崇尚‘善’。”“真情境”不仅强调学习情境的真实性,还表现为把儿童看作学习中的“真人”,即“真情境”一定是“有我之境”。
从学与教的价值出发,教,自然是“为学而教”“让学习真正发生”;学,则是“学会学习”。学生在习得知识、掌握技能的同时,获得人格的健全、精神的成长及素养的全面发展。而在数学学科中,学生数学素养的发展,归根结底是为了将所学应用于现实的、较复杂的情境中解决问题。那么,数学学习中,教师所创设的、服务于学与教的情境,其品质的高低,便对学生数学素养的形成与发展起到了至关重要的作用。
情境数学强调创设“真情境”,是因为在当下的一
些数学教学中,仍然存在着情境创设与学生的生活联系不紧,与周围世界联系不密,情境过于简洁、过于凝练等情形。
一方面,教材的编排、教师的设计,往往根据特定教学内容展开。在创设情境时,教师更多注重情境与相应数学知识的紧密关联,人为去除了诸多与教学内容无关,甚至是会发生干扰作用的因素。在这种“简洁”“凝练”的情境中,学生基本无需梳理、甄别,即可快速从中提取出相应的数学信息,提出问题,作出猜想,尝试解决。但我们发现,长期在这种境况下学习的学生,一旦走出课堂、走进生活,面对周围纷繁复杂的世界时,往往很少会主动地“用数学的眼光观察世界,用数学的思维分析世界,用数学的语言描述世界。”(史宁中语)因为,蕴藏于现实生活与周围世界中的数学,基本都不会像上述学习中的情境那样简单、明了。
另一方面,“数学是研究现实生活中数量关系与空间形式的科学。”(恩格斯语)教学中,我们往往过多注重了数学的“高于生活”,而对其“源于生活”重视不够。小学阶段,在引领学生学习作为人类文明发展成果的数学时,我们理应引导他们于“真情境”中经历数学的发现、发生与发展过程,感受数学之妙,体悟数学之用,发现数学之美,让学习在学与教的价值归一中走向深刻。
接下来,我将以“三角形”部分的两则案例为例,跟大家分享我的一些实践与思考。
【案例一】苏教版四年级下册《认识三角形》

《认识三角形》是小学阶段三角形板块的起始课。在这部分内容的学习中,学生将经历从现实生活中抽象出三角形,在观察、操作的基础上尝试用数学语言描述三角形,认识三角形各部分的名称等过程。教学中,教师一般借助教材提供的斜拉索桥图片(如上图)创设情境,也有教师会在此基础上呈现更多含有三角形的生活场景,进一步丰富教材创设的现实情境。但我们会发现,学生对这样的情境往往缺乏热情。究其原因,是这些场景看似源于现实生活,实则游离于学生的体验之外。学生主体体验的缺失,让情境少了“真人”,变成了“无我之境”。对此,李吉林老师强调:“儿童情境学习的第一步是走进周围世界,在儿童眼前展现一个活生生的、可以观、可以闻、可以触摸、可以与之对话的多彩的世界。”
受此启发,在本课教学前,我设计、开展了“寻访三角形”的数学活动。引领学生走出课堂、走进生活,去观察、发现“生活中哪些地方有着三角形的身影”,用相机记录,用笔描摹,与同伴交流发现,在本子上记录下疑问与思考。活动中,学生惊喜地发现“三角形原来就在我们身边!”“生活中其实并不缺少数学,缺少的是我们发现数学的双眼。”
苏霍姆林斯基在《把整个心灵献给孩子》一书中说,“学习如果具有思想、感情、创造、美和游戏的鲜艳色彩,那它就能成为孩子们深感兴趣和富有吸引力的事情”。而“寻访三角形”这一数学活动,正为学生的数学学习增添了几抹“鲜艳色彩”。活动结束后,当学生回归课堂时,他们的小脸满溢着喜悦,双眼绽放着光芒。他们纷纷争先恐后地展示自己拍下的照片,为大家比划自己找到的各种各样的三角形,叙述自己的发现与思考。在观察、记录、交流的基础上,学生发现,尽管大家找到的这些三角形形状、大小不同,使用的材料也不同,但都可以用“三根线条”描摹下来。这样的体会,再经过数学语言的修正,三角形的描述性概念便呼之欲出,数学的抽象也经由他们自己逐步展现。在随后的学习中,学生联系“分子结构图”中的三角形来认识它各部分的名称,借助“人字梯”的变化解释自己对三角形边、角、顶点间紧密联系的理解……周围世界这一“真情境”为他们的认识与思考提供了丰富且鲜活的素材,带动着他们的学习从生动不断走向了深刻。
在这个单元后续内容的学习中,我又欣喜地发现,学生总能主动将数学学习与周围世界紧密相连。“三角形三边关系”的学习中,他们借助“人字梯”巧妙地向同伴解释“三角形两边之和大于第三边”的道理;学习完“三角形的分类”后,他们又自信地告诉别人,“生活中经常能看到等腰三角形、等边三角形,是因为轴对称让它们更美。”
由此我感受到,“真情境”之“真”,首先便是真实,给学生一个真实的世界——走进生活,让“学科教学内容与儿童的真实生活相通”,让“符号学习与多彩生活链接”。
【案例二】苏教版四年级下册《三角形三边关系》

“三角形三边关系”这部分内容中,教材通过“任意选三根小棒,能围成一个三角形吗?”这一问题,为学生创设操作情境,引导学生在操作、观察、思考与交流中发现“三角形任意两边长度之和大于第三边”。但实际教学中我发现,在这样的操作情境中,学生的观察与思考更多聚焦于三根小棒的长度,往往缺少了对三角形的整体观察与思考。我们知道,三角形的边与角是紧密联系的。如果仅关注“边”,而忽视会与之联动变化的“角”,就失去了“数学是研究千变万化中不变的关系”(开普勒语)这一本意。基于这样的思考,我重设情境,进行了以下教学实践。
课始,利用课件呈现问题情境:小明家距学校300米,小红家距学校500米,他们两家之间相距多少米?
生:如果他们分别在学校的两边,就是800米;如果在同一边,就是200米。
师:明白他说的意思吗?你能分别画图表示出这两种情况吗?
(教师指导学生,画图时可以用图上的1厘米来表示实际的100米。随后组织开展交流)
师:大家发现了吗?如果我们把小明家、小红家和学校的位置都看作是一个点,那么在这两种情况中,这三个点都有什么共同的位置特征?
生:都在同一条直线上。
师:想一想,除了刚才这两种情况外,还会有其他情况吗?
生:这三个点也有可能不在同一条直线上。
师:当它们不在同一条直线上时,两家之间又会相距多少米呢?带着自己的思考,利用草稿本画一画、量一量,再到小组中交流你的答案。
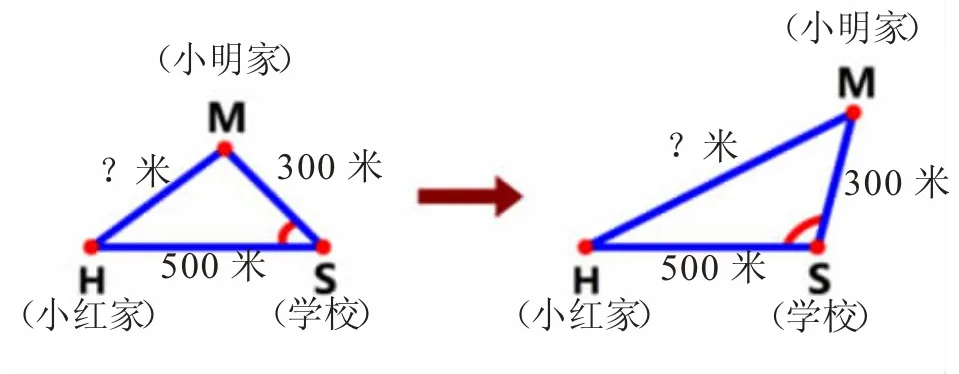
随后,在全班交流的基础上,通过对不同方案的观察、对比,学生发现:当三个点不在同一条直线上时,它们之间的连线就构成了一个三角形。而小明、小红两家间距离与∠MSH的大小有关。∠MSH越小,两家间的距离越小;∠MSH越大,两家间的距离越大(如下图)。由此得出:三角形中,固定长度的两边,夹角越大,对边越长;夹角越小,对边越短。再通过进一步的思考、交流与辨析,初步发现“三角形两边之和大于第三边”。
整节课中,学生始终饱含探究的热情。因为在不断深入地思考、观察、对比与交流中,他们获得了一个个新的发现,不断感受到了数学探究的乐趣。而这些,正源于教师根据教学内容的数学本质、学科特点、儿童特点所创设的问题情境。在这样的情境中,知识是有根、有背景的。正如李吉林老师所说,“人在境中,知识也在境,相互联系、相互依存。”如此,就使学生学习中的情感活动与认知活动有效结合起来,并推动着学习不断走向深刻。
由此我认识到,“真情境”之真,还应是本质、本真,为学生创设一个蕴含“真知”的优化情境,引领他们在探究与发现中获“真知”、激“真情”、启“真智”,获得真成长。
最后,我想说的是,教学中我们对“真情境”的追寻,还意味着对惯常教学的打破与重塑。因为时代在发展变化,学生也在发展变化,今天的学生不等同于过去的学生,未来的学生也不等同于今天的学生。因此,情境的选择与创设,应永远走在不断“寻真”的道路上。这条道路没有终点,但只要真正走上去,一个个驿站都是“真情境”。

