从『外输入』走向『内打破』——以《长方形和正方形的面积》教学为例

文 李余献

李嘉诚说：鸡蛋从外打破是食物，从内打破是生命！我想说：教学从外输入是教，从内打破是学！

【课前思考】

《长方形和正方形的面积》的教学，纵观其发展的历史痕迹，可以发现教学设计和教学行为随着目标定位的改变而改变。第一轮新课改之前，基本属于公式记忆，练习巩固教学方式，关注了公式记忆和运用的熟练。之后的十余年间，不仅关注了公式的记忆与运用，还关注了公式生成的过程与方法。在数学学科核心素养的背景下，原来的教学存在什么问题？通过深度思考，我们发现存在这样几种现象：一是课堂开放不够，顺教而学现象比较普遍；二是学科素养生长过少，侧重知识与技能的生长；三是公式理解不透，知道“面积=长×宽”，对公式的本质“格”与面积之间的联系不太明白。如何突破以上问题，直面学习内核，我们进行了以下的实践与思考。

【教学过程】

一、自主探究，新知建构

1.估一估，初感面积。

师：（出示一个面积为1平方分米的正方形纸片）同学们，我们已经学习了面积和面积单位，这个小正方形的面积是多少？

生：1平方分米。

师：如果这个小正方形纸片的大小为1平方分米，［出示一张3×4=12（平方分米）的长方形纸片］那么这张长方形纸片的面积大概会是多少呢？请你估一估。

生：10平方分米。

生：12平方分米。

……

2.试一试，初探方法。

师：这张纸片面积到底有多大？请你用自己的方法试一试。

（学生自主尝试后汇报）

生：面积是12平方分米，我是用1平方分米的小正方形摆出来的。

生：这张纸片可以折成12个1平方分米的小正方形，所以它的面积是12平方分米。

生：我把这张纸片画成12个1平方分米的小正方形，所以它的面积是12平方分米。

生：我量出这张纸片的长是4分米，宽是3分米，用3×4=12，就可以求出面积是12平方分米。

师：你们真厉害，分别用了摆一摆、折一折、画一画、量一量的方法知道了这个长方形纸片的面积。

3.看一看，构建表象。

师：你是怎么得到12平方分米的呢？明明是12格呀，为什么是12平方分米？

生：1格等于1平方分米，12格就是12平方分米。

师：老师从同学们那里找到了下面这几幅图，第一幅里很容易看出3×4=12（格），其他几幅图里，难道也有3×4=12（格）吗？你是怎么看出来的？

学生依次讨论，想象格子总数。

4.算一算，推导公式。

师：请大家在格子图上画一个你自己喜欢的长方形，并求出它们的面积。

（学生尝试后汇报）

师：你发现了什么？

生：长方形的面积=长×宽。

师：那正方形的面积该怎么计算？

生：正方形的面积=边长×边长。

师：为什么长×宽或边长×边长就是它们的面积呢？

生：因为“长×宽”或“边长×边长”可以求出有多少个格子数，每个格子数就是一个面积单位，所以格子数就相当于它们的面积大小了。

二、打破惯性，深度建构

师：下图中这个长方形的面积是多少平方分米？

生：3×2=6（平方分米）。

师：现在你还觉得是6平方分米吗？

生：不对不对，是24平方分米。

师：怎么变了？

生：因为一个格是4平方分米。

师：3×2=6，这里的单位应该是什么？

生：应该是6格。

师：下图中这个长方形的面积是多少平方分米？

生：3×2=6（平方分米）。

师：现在的面积可能变化吗？

生：不会。

师：从这两道题目里，你发现了什么？

生：有时候格子数是面积数，有时候格子数不是面积数。

三、生活沟通，建立“模型”

师：请计算下面几道题，结合今天学习的内容，你有什么发现吗？

生：它们都是用乘法计算。

生：马克笔一排的支数，就如长方形的长一样。马克笔的总支数，就如长方形的面积。

四、拓展延伸，凸显素养

练习一：请大家闭上眼睛，想象面积为24平方厘米的长方形，它可能长什么样子？伸出你们的小手描一描。

练习二：长6厘米、宽4厘米的长方形，它的面积是多少？（1）如果长增加1厘米，宽不变。面积增加多少平方厘米？（2）如果宽增加1厘米，长不变。面积增加多少平方厘米？（3）长宽同时增加1厘米，面积增加多少平方厘米？

（学生思考后汇报，课件出示结果）

五、全课回顾，总结提升（略）

【课后反思】

一、给足空间：为“内打破”创设格局

格局有多大，空间就有多大；空间有多大，思路就有多广。教学也是如此，教师越放手，学生的创新思维越容易被激活。如何放手？就是减少外因给与，增加内因的探索与发现，即减少教师对学生的指向性导入，增加学生自主性的独立思考与合作交流，大胆放手，给学生充足的时间和空间，让学生按照自己的想法去实践，去验证自己所学的东西，让内驱起作用，让内核发生改变。

1.从“给方法”走向“找方法”。

本节课不像许多教师那样，从一开始就指令性地让学生摆一摆或是画一画，而是出现一个单位面积为1平方分米的正方形，让学生摸一摸面积在哪里，然后出现一张长方形的纸片，让学生猜一猜面积有多大，再大胆放手让学生用自己的方法去探究长方形的面积。果然不出所料，越放手，学生的思维越容易被打开。首先在操作方法上，学生出现了摆一摆、折一折、画一画、量一量的好办法，最后在结果获得的方法上，有的学生用了数，大部分学生用了算。无论是操作方法还是结果获得的方法，都是学生自主思考后获得的成果。从“给方法”被动学习到“找方法”主动参与，学生的思维被打开，创新的做法自然就水到渠成了。

2.从“给图形”走向“创图形”。

在探究长方形面积公式从特殊到一般时，本节课不是教师给学生几个长方形让他们计算其面积，而是问“是不是所有的长方形都可以用这种方法得到它们的面积呢？请同学们自己在格子图上画一个长方形，并完成《练习单》”，让学生自由发挥，画自己喜欢的长方形，最后再汇报自己画的长方形的长、宽和面积。

在探究面积相同的长方形的多样性，初步感受面积相同形状不同、周长也不同的学习环节中，教师只给出了要求：面积为24平方厘米的长方形是什么样的？让学生把长方形画出来。这里不是给出几个面积一样的长方形让学生看着图形算出来，而是只给了学习要求，给了学生自由发挥的空间。

这一系列微妙的做法，看上去结果差不多，但实质是不一样的。从“给图形”到“给要求”，学生自然就会去“创图形”，在创图形的过程中，教师给学生的空间变大了，思维开放了，从“顺思维”走向了“逆思维”，思维的深度得到了很好的自我生长。

二、直面素养：为“内打破”高立目标

知识是暂时的，素养是长久的。如果只把目标定位在三维目标上，我们的目光会显得不够长远。如果能把目标定位在素养上，我们才能为学生未来考虑。如何针对学生未来的核心素养改进教学行为，正如史宁中教授所说，我们要培养学生会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界。

1.从平面图形走向数学模型。

平面图形的面积教学，大多数教师只会在图形推导的巷子里转，这样的教学学生只会记住面积公式。如果打破平面图形，让图形与生活邂逅，找到它们的共性，打通它们之间的任督二脉，学生的认知就不再只是徘徊在二维空间，数学模型就会在头脑中形成。

本节课通过三个环节完成数学模型的建构：

（1）初感模型。在课的第一环节，教师让学生用自己的方法得出长方形纸张的面积是多少。学生在摆一摆、折一折、画一画中初步感知3×4=12（格）的面积公式的模型。

（2）初建模型。接着在学生呈现的四种图形中寻找3×4=12（格），让学生在脑海里重复“行格数×列格数=总格数”模型；然后，让学生在格子图上自由地画出长方形，再写出面积计算的算式，又一次在头脑中建立一般长方形面积计算的模型。

（3）深化模型。本节课这个时候不是马上刹车，而是让学生列算式计算生活中的三道题，再出现长方形面积计算，让学生去找联系点、相关点、共同点。这个时候，留在学生脑海里的不再是面积公式，而是一种“长×宽”的思维模型。

2.从直观图像走向直观想象。

核心素养里的直观想象在图形教学中作为目标是必然的，但是如何利用这节课生长学生的直观想象能力，在本节课教学中有种“润物细无声”之感。

1.从形象到抽象。

在面积公式形成的过程中，教师把四种情况一一呈现在黑板上，这四种情况是有梯度的，从到，再到，最后到，实际上是一个从形象到抽象的过程，特别是最后一个，只有数据，教师让学生在每一个图形里找到3×4的格子，这种无中生有的教学，让学生眼前浮现看不见的格子，无形中培养了学生的空间想象能力。

2.从抽象到想象。

在练习中，本节课先绘声绘色地创设情境：有一个面积为24平方厘米的长方形，你觉得它可能长什么样子？请闭上你的眼睛，想象一下，它的长是几厘米？宽是几厘米？它的面积刚刚好是24平方厘米。现在请同学们伸出你的小手，把你脑海里的长方形在空中描出来，最后在格子图上画出来。在这个环节中，学生通过想象，对问题进行思考、分析，在脑海中浮现出格子的数量和长、宽，再在纸上涂出长方形来验证自己的想象。整个过程中，学生兴趣浓厚，觉得很好玩。不仅巩固了长方形的面积公式，更重要的是培养了空间想象能力。

3.从一维到二维。

在最后的一题练习中，本节课给出了三个问题：（1）长增加1厘米，面积增加多少？（2）宽增加1厘米，面积增加多少？（3）长和宽各增加1厘米，面积增加多少？

这三个问题有一个共同的特点就是给学生的是一维数据，而让学生想象的是二维数据在哪里？有多少？学生通过一维想二维，再验证二维数据的多少。学生在整个过程中不停想象，而且三个问题有一定的坡度，让学生感悟由于长、宽长度的变化，引起长方形面积的变化，帮助学生感受一维到二维的变化。这样教学，学生不但理解了面积的含义，而且提升了空间想象能力。

空间想象能力的最终形成，光靠“动手”是不够的，需要“手脑同步”“做思并进”。所以在设置练习时，尤其要凸显空间观念。学生从抽象的文字中，通过想象、分析，理解了面积的内涵，更促进学生由“实践表征”向“空间认知”的能力提升。

三、找到关键：为“内打破”提供核心

从教学任务看，“长方形的面积计算”属于规则学习，而非符号学习。许多教师在教学时关注了面积公式形成时的操作和公式的记忆。也就是说面积形成过程的程序化理解还是缺失的。之前调查了部分高年级的学生，问：长方形的面积公式你知道吗？你知道为什么是长乘宽？第一个问题几乎所有的学生都能作答，但对第二个问题，大部分学生就答不上来了。有的学生甚至说：长方形面积就是长乘宽，没有为什么呀！其实长方形面积公式的产生是一个用一维数据通过计算得出二维数据的过程，这个过程必须要弄明白“长度”与“面积单位”之间、“格”与“面积”之间的的关系。这两个关系弄明白了，才算真正理解为什么面积是长乘宽了。

1.从内容走向内核。

无论哪种图形，求面积的本质意义都是“探求所含面积的单位个数”。学生虽然从格子图中发现了“长方形的面积=长×宽”的规律，但是仅仅停留在数值上正好相等，并没有实质性地理解了面积的含义。

在学生得出4×3=12（平方分米）时，教师问：4表示什么？学生答：表示4个格子。3呢？表示3行，学生答。教师又问：4个格子乘以3，得出的结果是12个格子，怎么会是12平方分米呢？学生答：因为1格=1平方分米，12格=12平方分米。在这样的沟通中让学生还原了长乘宽等于面积的中间省去的环节，学生对面积的得出有了本质的理解。

2.从内核走向内化。

学生理解了“一格”与“面积单位”之间的关系后，本节课为了学生深度理解它们之间的关系，先出示下图一，学生受到思维定势的影响，回答为6平方分米。教师在图上出示一格为4平方分米的小正方形（大小与长方形里的一个相同），学生发现上当，马上改成24平方分米。然后教师又出示图二，学生得出结果为6平方分米。教师问：这个答案还可能变吗？学生回答说不会变了。然后，教师把两道题目放到了一起，问：同样都是6格，为什么题一不是6平方分米，而题二可以确定为6平方分米呢？学生说，看每一格的大小是不是确定的，告诉我们长、宽的长度，就可以确定每一格就是一个面积单位，但仅告诉我们格子数时，还不能确定每格就是面积单位。

求出长方形的面积是多少平方分米？

图一

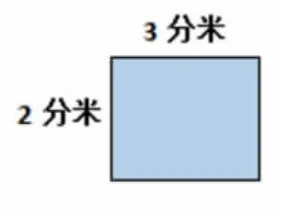
图二

通过本环节的学习，学生对格数、面积单位、长、宽和面积之间的关系完全掌握，深度理解了面积公式的本质。

一节好课，不只是站在“目前好”的视角进行设计与教学，而是站在“今后好”“越来越好”的视角去设计教学。一节好课，是因为已经跳出了眼前，站在了三维目标之外的学科核心素养和学习的本质。