带马尔可夫切换的混合随机系统的鲁棒稳定性

查明鑫，谢 涛，司文晓

(湖北师范大学 数学与统计学院，湖北 黄石 435002)

0 引言

近几十年来，非线性随机系统在控制工程中应用十分广泛，其系统的稳定性一直是人们关注的热点问题[1～18]，其中鲁棒性问题与控制系统的相对稳定性有密切的关系。鲁棒性作为传统的抗干扰特性,具体指控制系统在特征或参数摄动时仍能使性能指标的质量保持不变的特性。在实际问题中，系统特性或参数的扰动往往是不可避免的。因此，内部模型规则的建立是研究鲁棒性问题的一个重要环节。例如，文献[2]在一般的非线性模型中加入了噪声干扰，同时在非线性随机项上考虑了时变时滞，得到了具有两个时滞项的模型，刻画了系统中噪声强度的上界。文献[5]中考虑了带有中立项和随机扰动的非线性模型，通过添加三个不同位置的时变时滞得到了如下模型：

类似于这个系统，文献[6]在这个系统基础上加入了马尔可夫切换，得到了具有中立项和时变时滞的混合随机神经网络模型,并进行了鲁棒性分析。这种形式比较对称的系统，在没有时滞项的情况下，是由如下随机微分方程发展而来：

文献[7]在这个方程的漂移项和扩散项中加入时变时滞，讨论了其中一项或者两项都含有时滞时,系统的全局指数稳定性。文献[10]中考虑了一种输入到状态鲁棒稳定性，在递归神经网络的基础上加入马尔可夫切换和状态输入项，得到了一种新的神经网络模型。文献[11]考虑了一种分段偏差变元时滞，它关于时间序列分成超前项和滞后项，使得原来的系统变成了混合系统，通过加入随机扰动，分析了这种非线性模型的鲁棒性，求得了噪声扰动的上界。

受上述文献的启发，本文考虑带有马尔可夫切换和偏差变元时滞的随机系统的鲁棒稳定性,给定具有两个激活函数的稳定系统，加入偏差变元和随机扰动后，得到的系统仍是稳定的，从全局指数稳定的条件出发,得到扰动系统全局指数稳定的充分条件。

1 预备知识

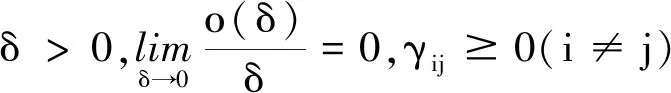
这里考虑如下带马尔可夫切换和偏差变元的混合随机非线性系统

(1)

其中y(t)=(y1(t),y2(t),…,yn(t))T为状态向量，β(t)表示偏差变元，固定两个实值序列αk和ηk，k∈,满足αk<αk+1，αk≤ηk≤αk+1且αk+1-αk≤α，这里α>0，对于任意的k∈，当k→+∞时，αk→+∞. 若t∈[αk,αk+1),分段变元函数β(t)=ηk. 这里A(r(t))=(aij(r(t)))n×n，B(r(t))=(bij(r(t)))n×n表示时滞反馈矩阵，函数f∶n×，n×+→n，g∶n×n×+→n×m,t0>0.ω(t)为定义在(Ω,F,P)上的独立于马尔可夫切换的m维布朗运动，在没有偏差变元的情况下系统(1)将变成如下形式：

(2)

记r(t)=i，A(i)=Ai，B(i)=Bi，i∈S. 假设系统(2)稳定，并且函数f,g满足如下条件：

假设1 对于任意的向量u1,u2,ν1,ν2∈n,t∈+存在一个常数k1>0使得

|f(u1,u2,t)-f(ν1,ν2,t)|≤k1(|u1-ν1|+|u2-ν2|)

且f(0,0,t)=0.

假设2 对于任意的向量u1,u2,ν1,ν2∈n,t∈+存在一个常数k2>0使得

|g(u1,u2,t)-g(ν1,ν2,t)|≤k2(|u1-ν1|+|u2-ν2|)

且g(0,0,t)=0.

易知，对于任意给定初值t0和y0,根据假设1～2，系统(1)存在唯一解y(t;t0,y0).此外，系统(1)还有一个平凡解y=0，同样系统(2)也有一个平凡解x=0.为不失一般性，假设系统(2)对于给定任意初值t0和x0,存在唯一解x(t;t0,x0). 为分析系统(1)和(2),现分别给出其均方指数稳定性的定义。

定义1 对于任意t0∈+,x0∈n,存在Δ>0和Λ>0使得

|x(t;t0,y0)|≤Δ|x0|e-Λ(t-t0),t≥t0≥0

成立，则系统(2)的解x(t;t0,x0)是全局指数稳定的。

定义2 对于任意t0∈+,y0∈n存在Δ>0和Λ>0使得

|y(t;t0,y0)|≤Δ|y0|e-Λ(t-t0),t≥t0≥0

几乎必然成立，则系统(1)的解y(t;t0,y0)是几乎必然指数稳定的。

定义3 对于任意t0∈+,y0∈n存在Δ>0和Λ>0使得

成立，则系统(1)的解y(t;t0,y0)是均方指数稳定的。

据以上定义2和定义3，由几乎必然指数稳定可以推得均方指数稳定，但反之不成立，因此在假设1和假设2成立的条件下，有以下引理。

引理1 若假设1和假设2成立，则系统(1)解的均方指数稳定意味着系统(1)解的几乎必然指数稳定。

引理2 当p≥2，h∶n×n×[t0,t]→n×m，使得则

特别地，当p=2时等式成立。

2 主要结论

为了描述系统(1)在时间t的解向量与偏差变元β(t)的关系，给出下面假设和引理。

假设3

引理3 令假设1～3成立，y(t)为系统(1)的解，则下列不等式

(3)

对于任意t∈+成立，其中

证明 对于任意t≥t0,由β(t)的定义,存在序列{αk},{ηk}使得

β(t)=ηk∈[αk,αk+1),t∈[αk,αk+1).

对于t≥ηk,由方程(1)得

(4)

令假设1和假设2成立,根据数学期望的性质和Cauchy-Schwarz不等式得

(5)

对(5)式应用Gronwall不等式得

交换(4)式中y(t)和y(ηk)的位置,类似于上述过程有

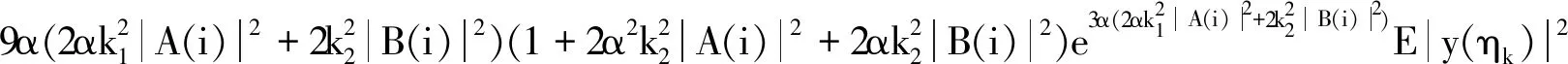
(6)

由(6)式整理得

(7)

这里

证明 将系统(1)和系统(2)满足初值的解向量写成y(t;t0,x0)≡y(t),x(t;t0,x0)≡x(t). 对于任意t≥t0≥0,由(1)和(2)得

(8)

由假设1和假设2,结合数学期望的性质和Cauchy-Schwarz不等式得

继续放缩

(9)

当t0+α≤t≤t0+2ρ时,由(9)得

(10)

这里

对(10)式应用Gronwall不等式

(11)

因此,对于t0+α≤t≤t0+2ρ

在区间t0+ρ-α≤t≤t0+2ρ-α有

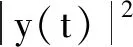
其中

λ=2Λ2e-2Δ(ρ-α)+2c1e2ρc2

(12)

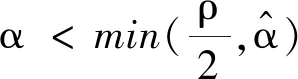
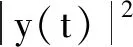
(13)

根据系统(1)解的存在唯一性以及动力系统流的性质,对于任意的正整数m有

y(t;t0,y0)=y(t;t0+(m-1)ρ,y(t0+(m-1)ρ;t0,y0))

结合(12)和(13)式,对于t≥t0+mρ-α时

|y(t;t0,y0)|=|y(t;t0+(m-1)ρ,y(t0+(m-1)ρ;t0,y0))|

≤e-ργ|y(t0+(m-1)ρ;t0,y0)|

≤e-mργ|y0|

因此,当t>t0+ρ-α,正整数m满足t0+(m-1)ρ-α≤t≤t0+mρ-α

(14)

显然,(14)式对于区间t0≤t≤t0+ρ-α仍然成立,说明系统(1)是均方指数稳定的,最后根据引理5,得到系统(1)是几乎必然指数稳定的。

3 应用举例

考虑如下多状态混合系统

(15)

由假设条件知k1=0.02,k2=0.03,马尔可夫链的生成元及参数为

根据文献[11],当Δ=1.2,Λ=0.9时,系统(15)是全局指数稳定的。

当偏差变元存在的情况下,具有马尔可夫切换的系统变为

(16)

其中β(t)∈[αk,αk+1),k∈.

图1描述了马尔可夫链中生成元Γ的轨迹。

图1 元Γ轨迹图

(17)

图2 系统(15)解的状态曲线

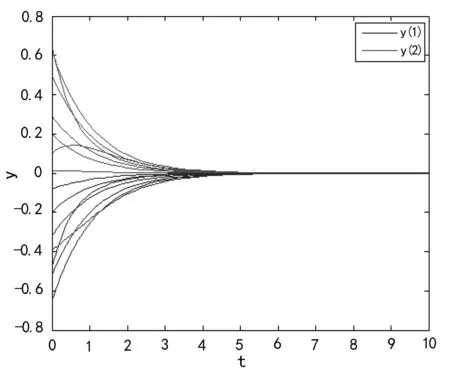
图3 系统(16)解的状态曲线