一类多维跳过程的最小熵鞅测度

李佳佳，沈兆晖

(武汉大学 数学与统计学院，湖北 武汉 430000)

0 引言

在金融市场中，我们经常用跳扩散过程对资产价格进行建模。风险中性测度则是资产定价时的一种常见概念和手段。由于在不完全市场中风险中性测度并不唯一，故我们经常考虑用某种准则选出合适的风险中性测度，比如：相对熵、逆相对熵、全变差距离、Hellinger 距离、最小鞅测度等。其中，相对熵是比较常见的一种准则。更确切的说，给定概率空间(Ω,F,P)，我们的目的是寻找鞅测度Q，并使其关于概率测度P的相对熵达到最小值。我们称鞅测度Q为最小熵鞅测度。

许多文献中有关于最小熵鞅测度的研究：参考Miyahara[1]，Mania 和Santacroce[2].特别的，指数Lévy过程的最小熵鞅测度在以下文献中得到讨论：Hubalek和Sgarra[3]，Miyahara[4]，Jeanblanc, Klöppel和Miya- hara[5].运用指数鞅方法研究一般跳扩散过程的最小熵鞅测度的文献比较少见，因此本文试图在这方面进一步研究。

在本文中我们应用相对熵准则，给出了多维跳过程S∶={(S1(t),S2(t),…,Sm(t),0≤t≤T}的最小熵鞅测度，其中Si(t)表示为：

1 一类多维跳过程的最小熵鞅测度

给定概率空间(Ω,F,P)，设S∶={(S1(t),S2(t),…,Sm(t),0≤t≤T}是定义在(Ω,F,P)上的m维价格过程，Si(t)表示为

(1)

其中σij为m×d1维矩阵，bi(t)(1≤i≤m)可微并bi(0)=0,B(t)=(B1(t),B2(t)，…,Bd1(t)),0≤t≤T为d1维布朗运动。fik(t,z),gik(t,z)为m×d2维函数矩阵并满足其元素关于t可料。

(2)

(3)

其中令G为F的子σ代数，则P(Ω,G)表示为G上的所有概率测度。

下面，我们引入相对熵的概念。令G为F的子σ代数，对于任意Q∈P(Ω,G)，可定义

(5)

在文中，我们的主要目的是给出在ALMM(P)上该价格过程S的最小熵鞅测度。首先，我们定义概率测度P*：

(6)

其中EP(·)表示关于P的期望，对于1≤i≤m，

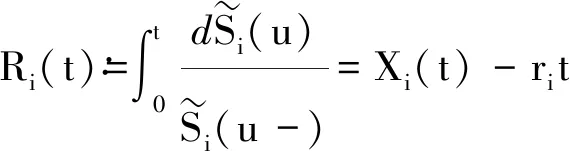
(8)

(9)

(10)

如此定义的P*称为Ri(t)关于P的Esscher变换[8].以下定理1为本文的主要结论，说明了Esscher变换P*即为价格过程S的最小熵鞅测度。

(11)

(12)

(13)

因此，{ez(t)≤t≤T},0为P鞅。

为了证明定理1的结论，我们给出以下两个引理。

2) 对于i=1,2,…,m,Gi(t)为P*鞅，其中

(14)

证明 1) 由分部积分公式可知，

d(W(t)ez(t))=ez(t-)dW(t)+W(t-)dez(t-)+[dW(t),dez]t

因此{W(t)ez(t),0≤t≤T}为P鞅，故{W(t),0≤t≤T}为P*鞅。

2) 我们将Gi(t)重新写成以下形式，

根据分部积分公式可知，

d(Gi(t)ez(t))=Gi(t-)dez(t)+ez(t-)dGi(t)+[dGi,dez]t

因此{Gi(t)ez(t),0≤t≤T}为P鞅，故{Gi(t)ez(t),0≤t≤T}为P*鞅。

引理2 (cf. Yan and Gao[7])

1)IG(Q,P)≥0当且仅当Q=P时等号成立，其中G⊆F.

2)IH(Q,P)≤IG(Q,P),其中H⊆G⊆F.

(15)

下面，我们来论证定理1的结论。

定理1的证明 令Q∈ALMM(P)，那么{Ri(t),0≤t≤T},1≤i≤m为Q局部鞅。故存在一列有界停时{Tn,n≥1}，满足当n→∞时Tn↑T，使得{Ri(t∧Tn),0≤t≤T},1≤i≤m为Q鞅。因为

故

由引理2(2)知，注意到FT⊇FTn,n≥1，我们有IFT(Q,P)≥IFT(Q,P),n≥1.而且，

由于{Ri(t∧Tn),0≤t≤T},1≤i≤m为Q鞅，可得出

EQ(Ri(Tn))=EQ(Ri(0))=0,1≤i≤m

且

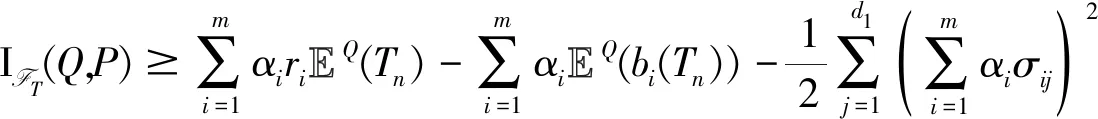
此外，令n→∞，我们可得出

因为Tn是有界的且Tn↑T.另一方面，

根据引理1知，

而且

因此

结合条件(10)，可以得出

(16)

证毕。

注记1 注意到ALMM(P)在P(Ω,FT)上为凸集合。同时注意到关于P的相对熵在P(Ω,FT)上严格凸，就是说，如果Q1,Q2∈P(Ω,FT)且Q1≠Q2,IFT(Qi,P)<∞对于i=1,2，那么

IFT(αQ1+(1-α)Q2,P)<αIFT(Q1,P)+(1-α)IFT(Q2,P)

对任何α∈(0,1)，结合以上性质，我们很容易得出最小熵鞅测度是唯一的。

2 一些特殊例子

接下来我们给出一些跳扩散过程的相关例子，并运用定理1中的结论可算得其最小熵鞅测度。实际上，我们可以变换如下过程的表达形式。

例1 [一类跳过程，cf. Yan and Gao[7]]令S∶={(S1(t),S2(t),……,Sm(t)),0≤t≤T}为概率空间(Ω,F,P)上的m维价格过程，Si(t)可表示为

(17)

下面，我们令

(18)

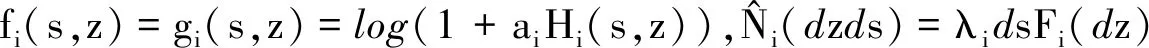
(19)

因此，Si(t)可写成如下形式：

(20)

根据定理1的结论可知，其最小熵鞅测度即为收益过程R(t)关于P的Esscher变换，且相对熵最小值为

(21)

这正是Yan and Gao[7]文章中结论的多维形式。

例2 [几何Lévy过程，cf. Fujiwara and Miyahara[6]]令S∶={(S1(t),S2(t),…,Sm(t)),0≤t≤T}为概率空间(Ω,F,P)上的m维几何Lévy过程，Si(t)可表示为

(22)

令

(23)

fi(s,z)=gi(s,z)=z

(24)

故，Si(t)可变换得到以下形式：

(25)

因此，定理1结论可知最小熵鞅测度即为R(t)关于P的Esscher变换，且相对熵最小值为

(26)

这是Fujiwara and Miyahara[6]中的结论的多维形式。