基于第一性原理对β-ThSi2力学和电子性质的研究*

郭永亮,陈俊彩,刘 潇,孔慧君,焦照勇

(1.河南工学院 理学部,河南 新乡 453003;2.河南师范大学 物理学院,河南 新乡 453007;3.河南工学院 电缆工程学院,河南 新乡 453003)

0 引言

相较于传统的各类发电站,核电站具有能量密度大、价格便宜、安全性高、环境友好、可靠性强等诸多优势。目前,核电站使用的主流核燃料是传统的铀235U,但是,据世界核能协会(World Nuclear Association)报道,地壳中铀的储量大约为5.7兆吨,以目前的消耗速度计算,仅够人类使用90余年。

另外一种可用于替代铀作为核燃料的材料是钍基材料。钍是一种具有放射性的金属,可以用来制作铀同位素233U。通过中子射击,钍232Th可以变成钍233Th,钍233Th先衰变为镤233Pa,然后衰变为铀233U。铀的这个同位素可以裂变,可当作核电站的燃料使用。目前,地壳中已探明的钍元素的储量是铀的三到四倍[1-3]。此外,作为未来的核燃料,钍比铀具有更多的优势:钍每吸收一个中子的产能高,消耗1吨钍产生的电量相当于200吨铀或3,500,000吨煤的发电量;钍基燃料循环产物中,钚的产量几乎可以忽略,利用钍废料去制造核武器几乎是不可能的;钍反应堆产生更少的核废料,长寿命的锕系放射性元素产量也很少[3, 4],因此它们无需大量、长时间地加以保存。半个多世纪以来,世界上许多国家已进行或正在进行钍燃料发电的研究。

在钍基材料核应用方面,我国40多年前就开展过钍基熔盐堆的研发,限于当时的技术条件,研发工作未能持续。随着经济、科技和工业能力的提升,我国于2011年重启钍基熔盐堆研究,即中科院战略性先导科技专项“未来先进核裂变能——钍基熔盐堆核能系统(TMSR)”[5-7],并已取得重大进展,为我国钍基熔盐堆研发开了个好头,但整体上这仍是一项极富挑战的长期任务[7]。

钍基硅化物Th-Si作为第四代反应堆的潜在核燃料之一,对其晶体结构及其相关性质的详细掌握在未来的实际应用中至关重要。钍基硅化物Th-Si体系主要以Th3Si2[8]、ThSi[8]、Th3Si5[9]和ThSi2[8, 10]等形式存在。早在20世纪50年代,美国普渡大学的Searcy等[8]合成了Th3Si2、ThSi和ThSi2,并采用X射线衍射方法研究了它们的晶体结构。近年来,Yagoubi等[11]在2013年采用高压同步X射线衍射方法对U-Si和Th-Si体系的晶体结构进行了研究,分析了这两个体系在高压下可能发生的相变;Zurek等[12]在2010年采用NMTO(muffin-tin orbitals of order N)技术对α-ThSi2和β-ThSi2的电子能带进行了研究。但总体来看,目前对此类材料的力学性能还缺乏更深入的研究。本研究采用密度泛函理论针对β-ThSi2进行详细的理论研究:通过分析其晶体结构、原子间的成键特性,进而研究其力学性能、计算相关的弹性模量、分析其稳定性;此外,我们对它的电子性质和光学性质也进行研究,以期为其实际应用提供一定的理论指导。

1 理论方法

在本研究中,所有计算都采用Materials Studio软件包的CASTEP模块[13]进行。采用超软赝势 (US-PP) 描述离子实与价电子之间的相互作用势。采用广义梯度近似(GGA)的Perdew-Burke-Ernzerhof (PBE)[14]交换关联泛函方法来求解Kohn-Sham方程,截断能设为600 eV。通过Monkhorst-Pack方案对β-ThSi2的晶胞的布里渊区进行14×12×12的k点网格采样,在允许离子位置、晶胞体积和形状自由改变的情况下优化晶格结构。当作用在每个离子上的力小于0.001 eV/Å时,认为晶体结构优化收敛。对于电子自洽的总能量的计算,收敛阈值设置为1×10-7eV/atom。

2 结果与讨论

2.1 晶体结构

ThSi2存在两种晶体结构,即α-ThSi2和β-ThSi2。其中,β-ThSi2晶体结构是AlB2型六方晶系,在低温下稳定,当温度达到1300～1350℃时相变为四方晶系α-ThSi2[8, 10, 11]。低温相β-ThSi2具有稳定的六方晶系层状结构,晶体结构如图1所示,空间群为P6/mmm,每个单胞中包含一个Th原子和两个Si原子。在基于密度泛函理论对材料性质进行模拟研究中,晶体结构准确与否对后续计算的精确度影响很大。通过对β-ThSi2的晶格结构进行充分的弛豫,获得较为准确的平衡态晶格,晶格常数a=b=4.118 Å,c=4.137Å。将其与前人已报道的实验结果[8, 10]进行对比,结果显示我们的理论值与实验值吻合得相对较好,如表1所示。另外,在晶胞中,Th原子占据的Wyckoff 位置为1a(0,0,0),Si原子占据的Wyckoff位置为2d(1/3, 2/3, 1/2),如表1所示。

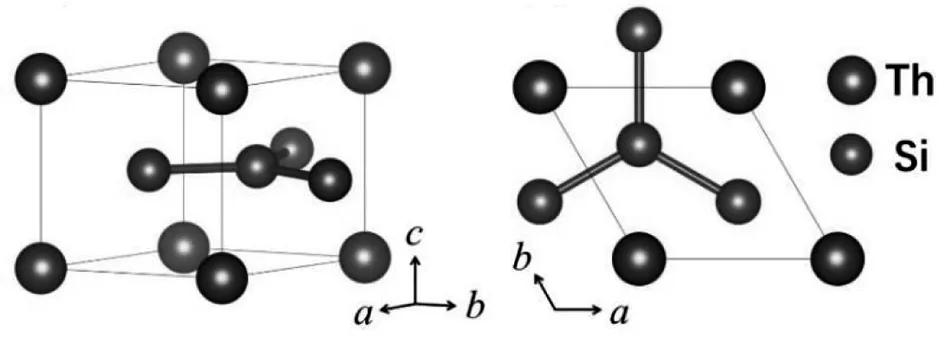
(a) 侧视图 (b) 俯视图

表1 β-ThSi2的晶格参数

2.2 弹性性质

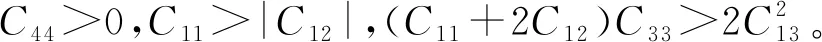
弹性模量,主要包含体积模量(Bulk modulus)、剪切模量(Shear modulus)和杨氏模量(Young’s modulus),是表征材料机械性能的基本参数。我们采用Voigt-Reuss-Hill近似[17-19],通过二阶弹性常数Cij计算β-ThSi2的体积模量、剪切模量、杨氏模量、泊松比(Possion’s ratio)和log-Euclidean各向异性参数AL,结果见表2。体积模量是衡量材料抗压缩能力的参数。我们计算的β-ThSi2的体积模量为94.0 GPa,略小于ThSi的体积模量 (98.6 GPa)[11]。作为对比,我们列出纯Th金属、ThC和ThN的体积模量,分别为58 GPa[20]、147 GPa[21]和175 GPa[22]。结果表明,β-ThSi2的硬度与ThSi相当,比纯Th金属高,但明显低于ThC和ThN。剪切模量描述了材料对剪切应力的响应。β-ThSi2的剪切模量为41.2 GPa,常见材料玻璃的剪切模量约为1.96 GPa,铅的约为6.8 GPa,纯铜的约为39～48 GPa,灰铸铁约为44.3 GPa。对剪切应力的响应方面,β-ThSi2与纯铜和灰铸铁相当。杨氏模量描述了材料在单轴应力作用下应力方向上的应变响应。本研究计算的β-ThSi2的杨氏模量为107.8 GPa,与之相对比,铝的杨氏模量约为69 GPa,纯铜的约为117 GPa,钢材的约为200 GPa,金刚石的约为1220 GPa,说明β-ThSi2对单轴应力的响应与纯铜相当。

表2 β-ThSi2的弹性常数和弹性模量 GPa

泊松比是指材料在单向受拉或受压时,横向正应变与轴向正应变的绝对值的比值,也叫横向变形系数,它是反映材料横向变形的弹性常数。通常泊松比的取值范围为-1～0.5。泊松比的值越大,材料的塑性越好。比如,大多数钢材在其弹性限度内的泊松比约为0.3,而橡胶的泊松比约为0.5。我们计算的β-ThSi2的泊松比为0.309,表明其塑性较好,与钢材相当。另外,体积模量与剪切模量的比值B/G,也能反映一种材料的塑性好坏。如果B/G大于1.75,此种材料的塑性较好;反之,它的塑性较差[23]。从表2我们可以看出,β-ThSi2的体积模量与剪切模量的比值B/G约为2.28,表现出较好的塑性,这与通过泊松比得出的结论吻合。

晶体材料的弹性各向异性描述材料的弹性性质随方向的变化,可由Kube提出的log-Euclidean各向异性参数AL来描述[24]。log-Euclidean各向异性参数AL是一种适用于各种对称性晶体材料各向异性的绝对测量方法,旨在量化某个系统的弹性性质在方向性上的依赖程度。AL值越大,则表示材料具有越明显的各向异性。我们计算的β-ThSi2的AL值为0.393,说明其有较明显的各向异性。据Kube报道,在他们测量的2176种晶体材料中,碳的各种同素异形体是各向异性最强的材料,其AL值分布于区间8.77～10.27;各向异性强于β-ThSi2(即AL>0.393)的材料仅占28%。

为了更详细地揭示弹性各向异性,我们计算了β-ThSi2的杨氏模量各向异性三维曲面,如图2所示。六方晶系的杨氏模量的各向异性可以表示为:

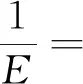
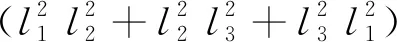
(1)

其中,l1、l2、l3为相对于三个坐标轴的方向余弦,Sij是弹性柔顺常数。对于理想的各向同性材料,其杨氏模量各向异性三维曲面应该是一个球体,而与球体的偏差反映了弹性各向异性的程度。由图2我们可以看出,β-ThSi2的杨氏模量各向异性三维曲面比较明显地偏离了球体,说明其具有明显的弹性各向异性,这与我们对log-Euclidean各向异性参数AL的分析结果相吻合。

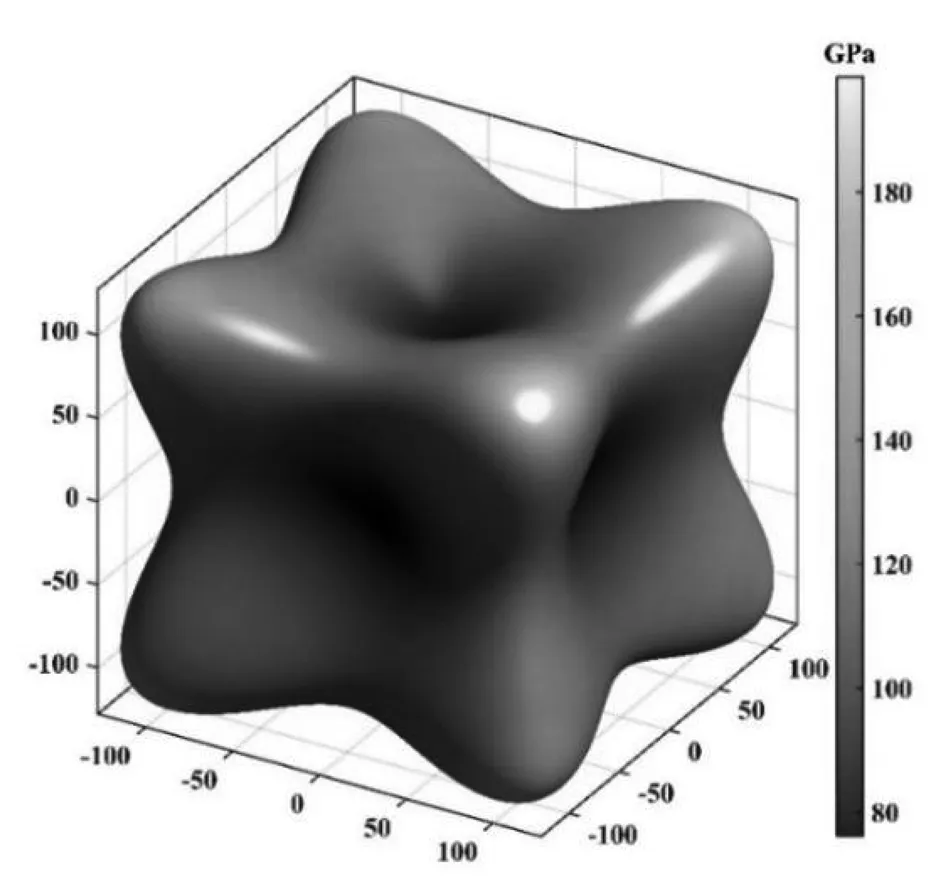
图2 β-ThSi2的杨氏模量各向异性三维曲面

2.3 电学性质

为了研究β-ThSi2的电学性质,我们计算了它的电子能带结构和态密度(DOS),如图3 (a)和(b)所示。从图3可以看出,β-ThSi2表现出金属特性,因为其能带穿过费米能级,在费米能级处,电子态密度不为零。图3(b)显示,费米能级附近的能态主要来自Th-d和Si-p电子的贡献,这说明β-ThSi2的导电性主要由Th-d和Si-p电子态决定。在费米能级以下的区域,电子能态主要来自Th-d和Si-p电子杂化,这是Th-Si成键作用的结果。在大于3 eV附近,由Th-d、Th-f和Si-p电子能态的杂化而形成了一个较强的峰。

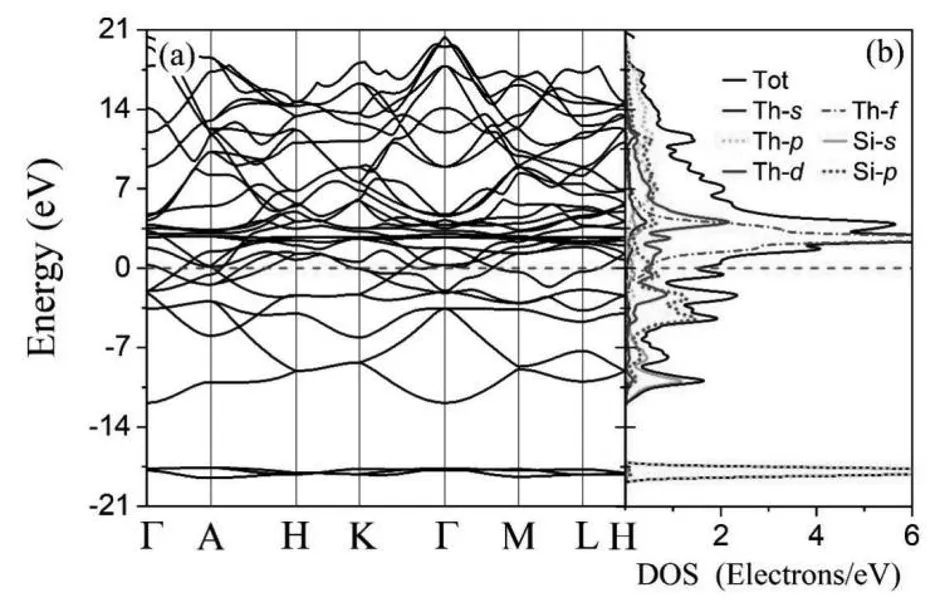
图3 β-ThSi2的电子能带结构(a)和电子态密度(b)

为了进一步研究β-ThSi2的电子结构,我们计算了它的电荷密度分布,如图4所示。由图4可以看出,由于Th原子半径较大,价电子数目较多,Th原子周围的电荷密度比Si高。Th原子的电子分布呈球形,这表明Th原子与其他原子没有形成共价键。最近邻的两个Si原子之间,电荷密度呈柱状分布,说明Si原子之间形成了共价键。此外,在Si和Th原子之间的区域电荷分布密度非常低,这证实了Th-Si键的离子性占主导地位。有趣的是关于Th原子的电子分布:Th原子在成键过程中有电子损失,在其周围也有电子积聚。这显然是Th原子间电子重排的结果,可以作为金属键出现的证据,亦是β-ThSi2表现出金属性的原因。综上所述,Si原子上同时形成了不同类型的键,即与Th原子形成离子键,与其最近邻Si原子形成共价键,而在Th原子之间形成了金属键。

图4 β-ThSi2的(110)面电荷密度分布(图中等高线间距为0.05 electrons/Bohr3)

3 结论

本研究采用第一性原理计算方法,针对β-ThSi2的晶体结构、弹性性质和电学性质进行了研究。β-ThSi2在低温环境下具有稳定的六方晶系层状结构,具有P6/mmm对称性。晶格常数分别为a=b=4.118 ,c=4.137 Å。β-ThSi2的弹性常数Cij满足Born-Huang稳定性判据,其力学结构是稳定的。弹性模量显示,β-ThSi2的硬度与ThSi相当,比纯Th金属高,但明显低于ThC和ThN;β-ThSi2表现出较好的塑性,与钢材相当;此外,β-ThSi2表现出明显的各向异性。电子结构计算结果表明,β-ThSi2表现出金属性,Th-Si之间形成离子键,Si-Si之间形成共价键,Th-Th原子之间形成金属键。