基于惯导误差特性的地磁匹配正交搜索方法

韩勇强，张延顺，陈家斌

(1. 北京理工大学 自动化学院，北京 100081；2. 北京航空航天大学 仪器科学与光电工程学院，北京 100191)

地磁导航与其他导航相比，可完全自主工作，具有隐蔽性好[1]、不受气候等条件限制的特点，是一种重要的自主导航定位手段[2-3].学者们在车载、地下、空中、室内和水下[4-8]等环境下进行了地磁匹配导航研究.地磁网格大小和匹配方法是影响匹配定位性能的两个重要因素.若地磁网格过小，匹配搜索的遍历时间将明显增加，且需要更大的存储空间.若地磁网格过大，地磁图网格量化误差过大，降低匹配定位精度[9-10].插值是解决这一矛盾的有效办法.基于MAD的匹配方法是快速简单实用的匹配方法[11-12]，适合工程应用.但高空高速飞行载体匹配导航对匹配定位时间提出了更严格的要求.因此，需要深入研究搜索策略，进一步提高系统实时性[13-14].

在地磁匹配搜索策略方面，LIU等[15]在研究没有先验磁性图的自动水下航行器(AUV)的导航问题时，提出了一种基于分段搜索策略的优化导航算法.LIN等[16]从INS得出的搜索窗口利用逐步外推法对最近点进行匹配搜索.以上方法从图像和数据处理角度改善了匹配性能.

利用惯性信息辅助也是提高匹配性能的有效方式.WANG等[17]为解决地磁图信息丰富度低时匹配精度低的问题，利用惯导解算轨迹所确定的三角形与BPNN神经网络训练地磁图等势线信息进行匹配,来获得最佳匹配位置.本文在高空高速飞行器采用的惯性系统误差特性分析基础上，研究基于惯导误差特性的正交搜索方法，并通过对延拓地磁图数据分析对所研究方法进行验证.

1 惯导误差特性分析

惯性系统误差与初始失准角和惯性器件误差有关，且误差随时间累积.对于应用地磁匹配定位的高空高速飞行器来说，航向精度是影响匹配效果的重要因素.由于高空高速飞行器导航系统选择惯性器件精度较高，所以，短期内陀螺漂移导致的航向角误差很小，航向误差主要表现为初始的航向失准角.航向角误差导致飞行器在飞行方向和与飞行方向垂直的方向分别产生位置误差.但这两个相互正交方向位置误差的投影不同.设飞行方向为X轴方向，则其定位误差特性如图1所示.

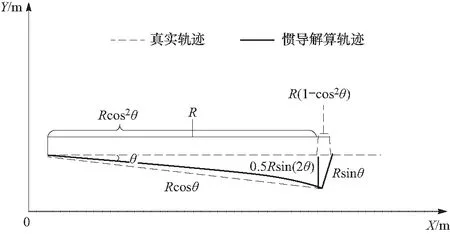
图1 惯导误差特性Fig.1 Inertial navigation error characteristics

图1中，θ为航向误差角，是惯导初始失准角和陀螺漂移产生误差角度的和.对于中、高精度惯导系统，短时间内陀螺漂移累积的误差角很小，所以θ包含的主要成份是初始失准角.R为实际飞行距离.由图1可以得出，惯导在解算过程中的X轴与Y轴方向惯性系统位置误差Xe和Ye分别为

Xe=R(1-cos2θ)

(1)

Ye=0.5Rsin(2θ)

(2)

由式(1)和式(2)可得出惯导发散误差在垂直方向和飞行方向位置误差的比例Δ为

Δ=Ye/Xe

(3)

由式(1)～(3)可得垂直方向和飞行方向惯性定位误差与误差角间的对应关系.

高空航向器中惯导系统航向误差角通常小于1°，所以本文下面分析0.1°～1°情况下垂直方向和飞行方向位置误差与航向误差角间的对应关系如图2和表1所示.

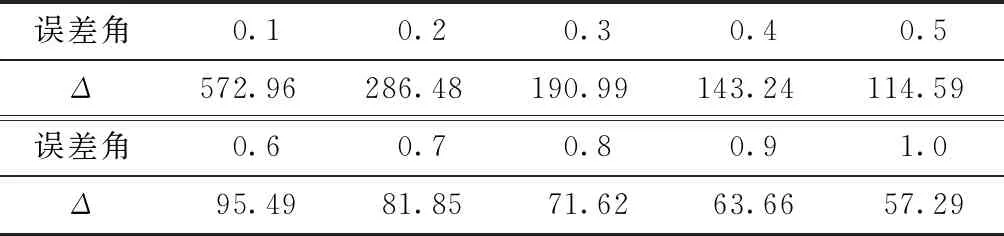
表1 惯性定位垂向误差与飞行方向误差比例

由表1和图2可见，在小角度情况下，在不同初始误差角情况下惯导轨迹垂直方向的位置误差都大于其飞行方向的位置误差.此现象可以作为地磁匹配定位中匹配搜索的先验条件，为改进搜索策略提供依据.高空远程飞行器惯导系统的器件精度通常较高，航向误差较小，垂向定位误差比飞行方向误差大的现象更加明显.因此，本文下面研究采用以惯导解算轨迹垂直方向搜索为主，飞行方向搜索为辅的正交搜索方法.

2 基于惯导误差特性的正交搜索方法

2.1 基于惯导误差特性的正交搜索方法总体思路

地磁匹配方法通常是采取多点地磁值匹配的方式.即先设置匹配序列点数，然后根据各匹配序列的地磁值与地磁图中网格格点上的对应值进行匹配.在搜索区域范围内进行遍历搜索，基于最小距离度量准则，找到最佳轮廓匹配位置.在此方法基础上，本文提出基于惯导误差特性的正交搜索方法.该方法首先利用地磁图中网格点上地磁数据插值生成惯导轨迹序列对应的地磁匹配序列，然后以此序列与地磁图中数据分别进行匹配，寻找基于最小距离度量准则下的最优位置.匹配过程中不再采用遍历搜索的方法，而是根据第1节所述高空飞行器惯导系统误差特性，先后在与载体航向的垂直方向和飞行方向分别进行搜索，这样既能提高搜索效率，又能提高准确性.本文方法流程如图3所示.

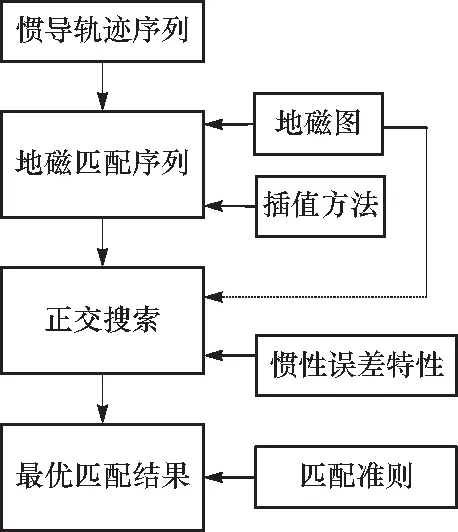
图3 基于惯导误差特性的正交搜索方法流程图Fig.3 Flow chart of orthogonal search mertod based on inertial navigation error characteristics

本文利用MAD算法对正交搜索的所有结果进行最小距离度量，选取匹配搜索结果中误差最小的位置作为当前时刻导航最佳位置点，以此来获得最优匹配结果.本文提出方法既能实现惯导解算轨迹匹配搜素过程中具体位置地磁值的计算，又能减少遍历搜索时间，实现精准、快速定位.

2.2 正交搜索方法

根据惯导误差发散特性分析可知，解算轨迹的垂向发散误差为主要误差，而平行方向误差为小量误差.根据惯导短期发散这一特性，先沿着惯导解算轨迹的垂直方向进行大范围平移搜索，在找到垂向最佳匹配位置后，再在飞行方向进行小范围搜索，最后确定总体最佳匹配位置，根据匹配位置对惯导解算轨迹进行位置校正更新.正交搜索方法如图4所示.

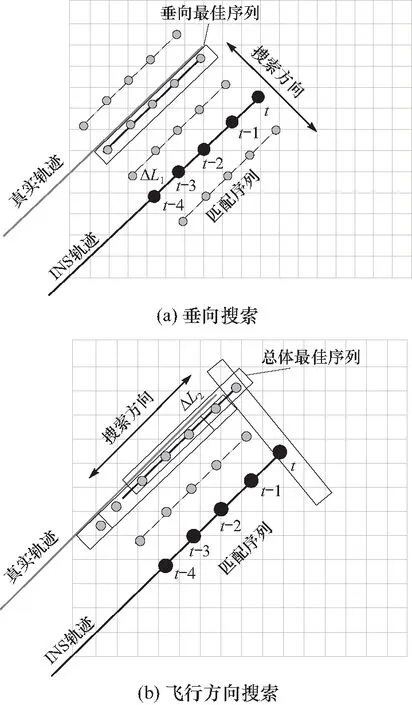
图4 正交搜索示意图Fig.4 Schemaric diagram of orthogonal search

上述红色点划线为真实轨迹，蓝线实线为惯导解算轨迹，黑色大实点是插值后生成的地磁匹配序列，绿色小实点是搜索匹配过程中匹配序列，双向箭头为插值后匹配序列匹配搜索的方向.

图4(a)表示垂向搜索过程，即插值后生成的地磁匹配序列沿与飞行方向垂直平面内进行搜索匹配.其中，搜索步长ΔL1按地磁图网格大小选取，而搜索范围按预估惯导误差的1.2倍选取.在搜索范围内找到真值附近的垂向最佳序列.

图4(b)表示地磁匹配序列沿与飞行方向平行的方向进行搜索、匹配，对上一步垂向搜索匹配后的垂向最佳序列进行平移微调，最后在圴方误差最小意义下得到总体上最佳匹配序列，从而实现精确定位.匹配完成后对惯导轨迹进行校正.

3 仿真研究

在以上方法研究基础上，将地面实测地磁图数据分别延拓到1 000，5 000，10 000和20 000 m高空，分别生成对应的高空地磁图，用于本文方法验证.与地磁图对应，设计飞行载体的运动轨迹.沿飞行轨迹分别采用遍历搜索和本文正交搜索方法进行地磁匹配，并通过数据分析证明本文方法的性能.对比中均采用MAD匹配算法，匹配精度一致.所以，下面数据分析中，本文主要对两种搜索方法耗费的时间指标进行对比.

本部分研究的地磁图数据是由课题组低空地磁数据采用FFT向上延拓算法生成.在Matlab环境下运行程序.

设计飞行载体的运动轨迹的参数和传感器误差如下.轨迹参数为：起始纬度30°，经度107°，飞行时长4 000 s，飞行速度1 km/s.初始失准角为0.1°，初始速度误差为0.02 m/s.陀螺零偏稳定性为0.05 (°)/h、加速度计0偏稳定性为100 μg.按上面方法和参数分别对1，5，10和20 km高空进行处理.定位结果分别如图5所示.

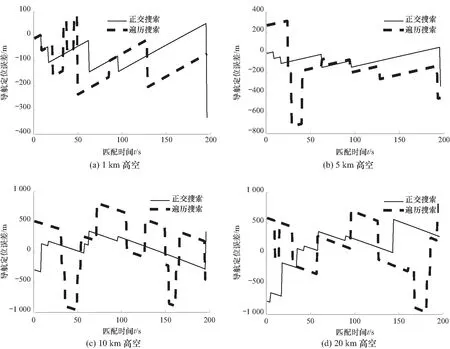
图5 两种搜索方式的匹配定位误差曲线对比图Fig.5 Comparison of the error curves of the matching and positiong of the twk cesrch methods

表2 两种匹配搜索方法的定位误差特性

由图5和表2数据可见，采用遍历搜索与正交搜索均能实现匹配定位，精度相当，且采用本文方法的定位精度均优于遍历搜索方法的定位精度.遍历搜索是在整个大区间内进行搜索，而本文方法是在真值附近的小区域内进行搜索.所以二者定位精度相当，但两种搜索方法所用的时间不同.表3是利用不同高度地磁图进行匹配定位时搜索时间的对比情况.

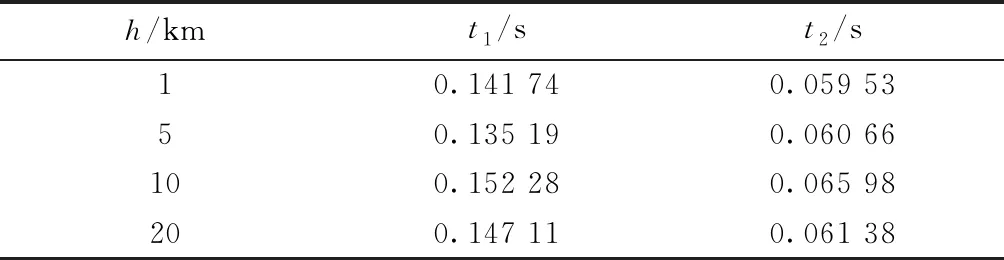
表3 遍历搜索与正交搜索时间对比图

上表中t1表示遍历搜索一次平均消耗的时间，t2表示正交搜索一次平均消耗的时间，从表3可以看出，在各高度地磁图中进行地磁匹配定位时，正交搜索的所用时间都小于传统遍历搜索方法耗费时间.其中，在1 km地磁图中，正交搜索方法所用的时间是遍历搜索方法的41.8%，匹配效率提高了58.2%.同理在5，10和20 km地磁图中，本文提出方法的匹配效率分别提高了55.2%，56.7%和58.3%.总体来看，正交搜索方法的应用，在保证了匹配精度的前提下，提高了匹配搜索效率.所以本文方法能改善高空高速飞行器匹配定位方法的实时性，具有良好的应用前景.

4 结 论

综合考虑匹配时效性和高精度定位要求，采取具有匹配精度高、算法简单、解算时间短的MAD算法作为本文方法的研究基础.为了克服传统搜索方法在大区域遍历搜索的盲目性、提高匹配效率、避免匹配区域过大等势线的干扰，本文利用惯导误差特性，通过定性与定量分析，提出正交搜索方法，在保证匹配定位精度的基础上，将匹配定位的效率提高了50%以上.本文提出的正交搜索方法不仅保证了定位精度要求，且实现了快速定位，适用于不同高度、不同速度、不同航迹的地磁匹配导航.特别对高空高速飞行器地磁匹配导航有很好的适用性.