考虑含水率干密度的土壤动态球形空腔膨胀理论

武海军，曾费隐，李金柱，皮爱国

(北京理工大学 爆炸科学与技术国家重点实验室，北京 100081)

在较多地下工事中，钢筋混凝土结构由覆盖的土壤加以防护，弹体必须穿透覆盖土层才能攻击到工事结构，因此研究弹体在土壤中的运动规律已逐渐成为学者关注的问题. FORRESTAL等[1]采用带Tresca极限的Mohr-Coulomb屈服准则推导了土壤动态球形空腔膨胀理论模型. SHI等[2]引入多孔材料状态方程，研究了土壤材料在空腔膨胀过程中空腔表面径向应力和空腔膨胀速度的关系. 谭仪忠等[3]采用了可以描述冻土特性的摩尔-库伦强度准则推导冻土材料的空腔膨胀阻力模型.

从空腔膨胀理论模型的应用发现，不同本构模型与屈服准则的选取会对计算结果有所影响. GITAU等[4]通过研究发现土壤抗剪强度与含水量之间呈负相关，许旭堂等[5]和GOEBEL等[6]也分别对土壤进行直剪实验，发现土壤的剪切强度受干密度与含水率影响. 在土壤空腔膨胀研究中，一般采用Mohr-Coulomb屈服准则进行分析，但该准则未考虑土壤材料物理性质对该屈服准则的影响，因此会影响其理论模型的精度.

鉴于以上原因，引入干密度与含水率对Mohr-Coulomb屈服准则进行修正，并对土壤动态球形空腔膨胀进行求解，获得空腔表面径向应力与空腔膨胀速度关系. 在此基础上，分析了含水率、干密度对空腔表面径向应力的影响；最后，对文献中实验数据进行计算并与常用经验公式计算结果进行对比，验证了模型的可靠性.

1 土壤材料的力学特性

土壤作为一种三相复合材料，由固、液、气三相组成. 由于孔隙的存在，土壤表现出与多孔材料类似的力学特性. 本文基于文献[2]选择p-α状态方程对土壤进行描述，可表示为

(1)

式中：ρ和ρs分别为土壤瞬时和完全压实时的密度；pe为土壤弹性极限压力；ps为土壤完全压实压力；α0为初始孔隙比.

同时，采用Mohr-Coulomb准则描述土壤材料屈服特性，模型可以表示为

σr-σθ=

(2)

式中：σr和σθ分别为土壤材料所受径向及切向应力；τm为土壤材料的最大剪切强度；pc为剪切饱和临界状态静水压力；C和φ分别为土壤内摩擦力和内摩擦角.

土体中含水率影响其孔隙中水分子状态，含水率的增加会使土壤中的结合水向自由水转变，同时水会溶解土中相关化学物质，降低颗粒间胶结作用力和范德华力，导致内粘聚力的降低；土体干密度会影响土颗粒间距离，干密度越大，颗粒接触越密实，其距离越小，使颗粒间胶结作用力、范德华力及静电力增大，导致内粘聚力的增加. 由许旭堂等[5]研究可知，内粘聚力受含水率、干密度等因素影响较大，而内摩擦角所受影响较小. 因此基于文献[5]引入含水率、干密度对式(2)进行修正，以体现二者对土壤屈服特性的影响.

σr-σθ=

(3)

式中：ω为含水率；ρd为干密度.

2 动态球形空腔膨胀理论

2.1 响应区的划分及各交界面跳跃条件

基于上述的土壤材料的本构模型，考虑弹靶作用过程，对土壤空腔膨胀过程进行分区，如图1所示.

图1 基于p-α状态方程的土壤动态球形空腔膨胀分区图Fig.1 Response regions of the soil depended on p-α EOS

响应区依次分为：弹性区、剪切未饱和区、剪切饱和区、密实区和空腔. 在弹性区中，材料处于弹性状态，应力应变关系遵循Hooke定律；在剪切未饱和区中，材料处于塑性状态，满足Mohr-Coulomb屈服准则；在剪切饱和区和密实区中，材料也处于塑性状态，并且遵循 Tresca屈服准则，但二者遵循p-α状态方程的不同区域. 图中r为径向球坐标，各区域界面坐标为交界面传播速度乘以时间.

在动态球形空腔膨胀过程中，各界面间物理量应遵从Hugoniont跳跃条件：

(4)

式中：ρi -和ρi +分别对应第i个交界面两侧的土壤密度；vi -和vi +分别对应交界面两侧的粒子速度；σi -和σi +分别对应交界面两侧的径向应力；ci为第i个交界面传播速度. 为方便后续计算，引入量纲一粒子速度Ui及量纲一径向应力Si对Hugoniont跳跃条件进行处理，得到

(5)

2.2 动态球形空腔膨胀响应分区分析

2.2.1弹性区

在弹性区中，土壤材料处于弹性状态，其压力范围可以表示为：p≤pe. 根据材料的状态方程，采用Hooke定律对材料的应力-应变关系进行描述，材料弹性区动量守恒方程可以表示为

(6)

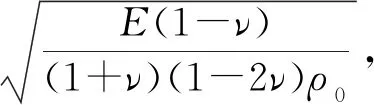
(7a)

(7b)

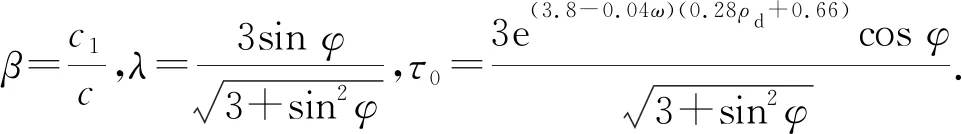
2.2.2剪切未饱和区

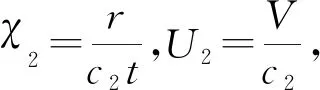
(8)

2.2.3剪切饱和区

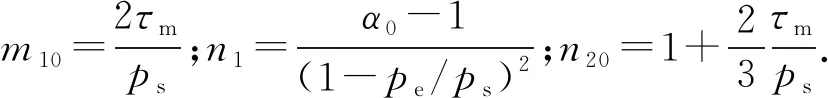
2.2.4密实区

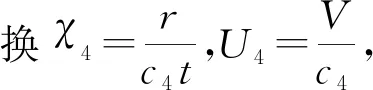
(10)

根据文献[2]，可以由式(6)得到各界面间的Hugoniont跳跃条件. 在弹性区与剪切未饱和区交界面处，有U2-=U1+，S2-=S1+；在剪切未饱和区与剪切饱和区交界面处，有U3-=U2+，S3-=S2+；在剪切饱和区与密实区交界面处，有U4-=U3+，S4-=S3+.

至此完成了土壤动态球形空腔膨胀所有区域的推导，通过数值计算可以拟合获得一组空腔膨胀速度和径向应力的关系. 在推导中采用含水率与干密度对土壤材料屈服准则进行修正，因此该靶体阻力函数也可以在一定程度上反映干密度与含水率对靶体阻力的影响.

3 理论计算与验证

基于空腔膨胀理论推导，获得了靶体阻力函数，并讨论了含水率与干密度对空腔表面径向应力的影响；采用FORRESTAL等[1]的处理方法，对刚性弹的侵彻深度进行计算，结合文献中的侵彻实验数据，验证理论模型的可靠性.

3.1 空腔膨胀速度与空腔表面径向应力计算

图2为土壤材料空腔表面径向应力σr与空腔表面膨胀速度V的关系图，求解过程中取ω=0.2，ρd=2 500 kg/m3. 根据文献[7]对图中数值结果进行二次拟合可得如下关系式：

σr=a1V2+a2V+a3

(11)

式中：材料惯性项系数a1=1 346 kg·m-3； 材料粘滞阻力项系数a2=132 307 kg·m-1·s-1； 材料强度项系数a3=23.8 MPa. 文献[8]中C23混凝土的球形动态空腔膨胀各项系数对应的值分别为5 145 kg·m-3，894 419 kg·m-1·s-1，108 MPa. 可以看到，土壤相较于混凝土在材料惯性项系数a1，材料粘滞阻力项系数a2，材料强度项系数a3上均有不同程度的降低. 同时发现在速度低于130 m/s时，材料强度对于空腔径向应力的影响高于材料惯性的影响；随着速度不断增加材料惯性与材料粘滞阻力的影响逐渐增加，而强度项影响相对减小.

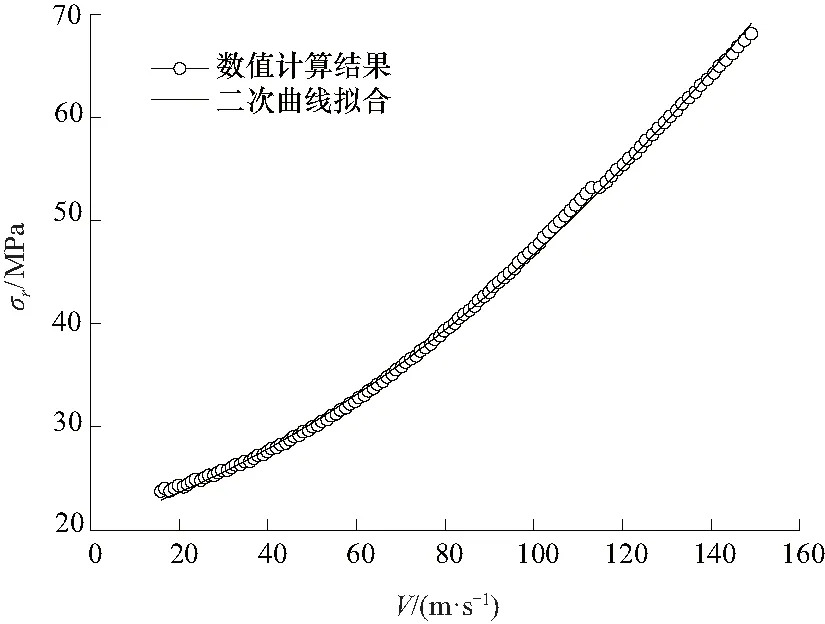
图2 数值计算结果Fig.2 Numerical simulation results

3.2 干密度、含水率对空腔表面径向应力的影响与讨论

选取不同的干密度和含水率对土壤材料动态球形空腔膨胀过程进行计算，探究各参数对空腔表面径向应力与空腔表面膨胀速度的影响. 为了简化问题，本节在动态求解过程中，采用控制单一变量的处理方法以研究不同参数的影响. 图3为不同干密度及含水率下，空腔表面膨胀速度和空腔表面径向应力的关系.

图3(a)表明，在相同的含水率下，在较低的空腔膨胀速度时，空腔表面径向应力会随着干密度的增加而增高，随着速度的增加，由于土壤被压实使得不同干密度的土壤力学特性接近，其空腔表面径向应力受干密度影响逐渐降低. 图3(b)表明，在相同的干密度下，含水率与空腔表面径向应力呈负相关，空腔表面径向应力会随着含水率的增加而降低. 与干密度类似，随着速度增加，含水率的影响也逐渐不显著.

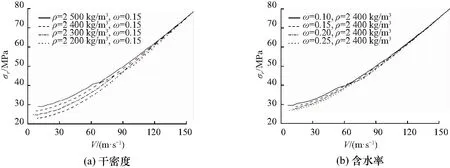
图3 不同干密度及含水率参数下空腔表面膨胀速度和空腔表面径向应力关系图Fig.3 Relationships of cavity velocity and radial stress under different dry densities and moisture contents

3.3 弹体侵彻土壤实验验证与讨论

基于3.1节推导的空腔表面径向应力与空腔膨胀速度关系，参考文献[8]建立刚性弹体侵彻土壤靶阻力模型. 在土壤中，由于其弹性波波速较低，本文计算得到的空腔膨胀速度最大为270 m/s，对于CRH为3的弹体，本文提出的侵彻阻力模型可以计算的最大初速为360 m/s. 因此，弹靶基本参数选取何翔等[9]实验如表1所示，其中弹体质量为286 g，弹头长度为140 mm，实验结果如表2所示.

表1 弹靶的基本参数

表2 侵彻实验结果

选取常用的YOUNG公式、别列赞公式[10]以及FORRETSAL模型对该实验进行了计算. 图4为上述不同计算模型得到侵彻深度与实验结果的对比图. 从图中可以看到别列赞公式的计算结果偏保守，YOUNG公式与FORRETSAL模型显示出一定的计算精度，而采用空腔膨胀模型计算得到的结果和其他公式相比与实验结果更为贴近，显示出较高的准确性，说明本文针对土壤屈服准则的修正以及后续空腔膨胀理论的推导是合理且可行的.

图4 各模型计算结果与实验结果对比Fig.4 Comparisons of results between different models and experiment

表3为各计算模型对实验工况的计算侵深h与误差δ对比. 从表中可以看到，在低速情况下，本文所提出的方法和YOUNG公式均有较好的精度；同时随着侵彻速度的增加，YOUNG公式的误差逐渐增大，本文计算结果与FORRESTAL模型计算结果在较高速度下有着较好的准确性.

分析认为，虽然YOUNG公式通过引入S数考虑土壤的含水率，但由于在公式中对S数没有定量分析，在计算过程中其S数并不会发生变化. 在实际中，土壤材料力学行为会随着侵彻运动而发生变化，尤其是随着速度增加，其力学行为变化也会增大，因此YOUNG公式会随着速度的增加，误差变大. 同样的，FORRESTAL模型在计算过程中也忽略了土壤动态变化对其力学行为的影响，使得计算过程中弹体所受侵彻阻力偏低，进而在侵彻深度计算上产生误差. 本文提出的空腔膨胀模型考虑了侵彻过程中土壤材料力学行为的变化，因此对弹体所受阻力有着较好的预估，使得计算结果有较好的准确性.

以上分析表明，前人总结获得的经验公式及侵彻模型可以在一定程度上对土壤侵深进行估算，但由于对土壤物理性质的影响考虑并不周全，使得计算结果有较大误差；而本文获得的考虑含水率及干密度的空腔膨胀模型，具有较高的计算精度.

表3 各计算模型的计算结果与误差对比

4 结 论

本文通过引入含水率与干密度对土壤材料的Mohr-Coulomb准则进行修正，用以描述土壤材料塑性区的强度特性，在此基础上完成材料动态球形空腔膨胀过程的推导，对材料空腔表面径向应力受干密度及含水率的影响进行了分析，空腔表面径向应力随着土壤干密度的增加而增大，随着土壤含水率的增加而降低，同时二者的影响会随着空腔膨胀速度的增加而逐渐降低. 通过与实验结果及常用公式计算结果的比较，验证了模型的合理性与准确性，该模型能较客观的反映土壤材料特性，可为不同土壤深埋地下工事的防护技术的研究提供理论支撑.