一种检测S盒能量信息泄漏的t检验方法

严迎建, 郑震, 郭朋飞, 朱春生

(战略支援部队信息工程大学 密码工程学院,河南,郑州 450001)

1 t检验检测能量信息泄漏的步骤

对密码设备侧信道能量信息泄漏的检测是目前侧信道领域受关注度较高的研究方向.对能量信息泄漏进行检测时，往往不要求对泄漏的具体情况进行精确地描述，而只需确定在一定的安全级别下是否能够检测到能量消耗中的信息泄漏[1].t检验法是能够满足这种需求的一种较为简单易行的能量信息泄漏检测方法，t检验结果描述了被检测密码算法能量信息泄漏的情况，该值超出一定的阈值时可以判定能够检测出能量信息泄漏，否则判定不能检测出泄漏[2].

目前国内外对t检验法检测能量信息泄漏的相关研究不够具体，对t检验位的受检顺序的研究较少，多以从前到后或随机的顺序进行检验[3-4].这样的检验方法效率较低，因此有必要对t检验位的排序方法进行研究以提高t检验效率.

分组密码运行过程中字节代替变换(S盒)处存在能量信息泄漏的概率最大[5-7]，本文以DES算法为例，将S盒输出这一关键中间状态设置为t检验位，对分组密码的能量信息泄漏实施t检验过程中检验位排序的问题进行研究，通过建立S盒的非线性性质与能量信息泄漏之间的联系，提出一种检测分组密码S盒能量信息泄漏的t检验方法.

t检验是统计学中假设检验问题的一种基本方法，对能量信息泄漏情况实施t检验的假设检验问题可以叙述成：在显著性水平α下，检验零假设H0：在一定安全级别下所选检验位数值对该时间点处的能耗没有影响，即在给定的检验标准下不能检测出能量信息泄漏.t检验的具体步骤如下[8].

(1) 能耗采集.

对密码算法运行过程中的能耗进行采集，得到n条能量迹Ti(i∈{1，2,…,n})，其中每条包含m个采样点{Ti(1)，Ti(2)，…,Ti(m)}.

(2) 分组.

选择密码算法的某中间节点作为检验位，记作Di.而后选定能量迹中的采样点，根据Di的数值将能量迹分为Ψ0和Ψ1两组：

Ψ0={Ti|Di=0},Ψ1={Ti|Di=1}

(1)

需要指出的是t检验位的选取并不局限于单比特，同样地可以选择多比特作为检验位.此时需要设置一特定的数值x，在选定的采样点处根据所选检验位多比特的值是否等于x将能量迹分为Ψ0和Ψ1两组：

Ψ0={Ti|Di=x},Ψ1={Ti|Di≠x}

(2)

在实际中对泄漏进行检测时，由于明文、密钥和设备运行情况等信息未知，要同时获取中间状态多比特的信息往往存在较大难度，因此本文只对检验位位宽为1 bit的情况进行研究.

(3) 处理能耗数据.

(3)

按式(4)计算自由度v为

(4)

再由自由度v可得到t分布的概率密度函数：

(5)

其中Γ表示伽马函数.由式(5)进一步可得到t检验中零假设成立的概率：

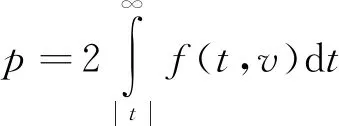
(6)

也可通过式(7)得出分布函数：

(7)

其中2F1表示超几何函数.而后进一步得到t检验中零假设成立的概率：

p=2F(-|t|,v)

(8)

(4) 比较分析，得出结论.

进行上述完整t检验的计算量较大且检验过程较复杂，因此在实际检验中可以采取简化的t检验方法：不考虑自由度、概率密度函数和分布函数等参量而只对统计量t进行计算，根据t值是否超出阈值得出是否能够检测出信息泄漏的结论.可以参考式(9)对阈值进行设置：

p=2F(t=±4.5,v>1 000)<0.000 01

(9)

式(9)表明，样本量大于1 000时，将统计量t的阈值设置为4.5,能够使得检验的准确率达到99.999%以上.简便起见，本文选择|t|=4.5作为阈值实施t检验，当计算得到的|t|>4.5时判定两组数据间存在差异，即能够检测出能量信息的泄漏；否则判定不能检测到泄漏.

2 对S盒实施t检验的排序方法

S盒是分组密码的核心部分，在加解密过程中起到混乱和局部扩散等作用：S盒输入中一个比特的不同会导致输出中多个比特的不同.S盒的非线性度越大，其达到的混乱和局部扩散的效果越好.在对S盒进行设计时为应对差分分析、线性分析和代数计算攻击等传统密码分析手段，要求其具有良好的非线性性质，即要求其具有较大的非线性度[9].另一方面，良好的非线性性质即较大的非线性度容易在侧信道能量分析攻击等新型密码分析手段中被攻击者利用. 从这一矛盾出发，对现有t检验方法进行创新.

2.1 S盒非线性度

S盒的实质是多输入多输出布尔函数，其性质可以用相应的布尔函数的性质进行刻画.

(1) 布尔函数的Walsh变换.

Walsh谱可以将布尔函数的特征表示出来，通过研究Walsh变换可以更好地对布尔函数的性质进行把握，n元布尔函f(x)数的第一种Walsh变换为[10]

(10)

其中，x=(x1,x2,…,xn)∈GF(2)n，ω=(ω1,ω2,…,ωn)∈GF(2)n，ω·x为ω与x的点积.

ω·x=ω1x1+ω2x2+…+ωnxn

(11)

f(x)的第二种Walsh变换为[10]

(12)

(2) 布尔函数的非线性度.

在阿根廷最知名的葡萄酒产区——门多萨（Mendoza）举行的国际葡萄采收节，时间为从12月持续到次年2月，举办范围为门多萨的18个地区。节日里，游客除了可以在葡萄园附近品尝美味优质的葡萄酒，还可以参加以葡萄酒为主题的巡游和派对。在酒节结束的那一天，会在一个具有希腊风格的竞技场中举办一场表演活动，由超过2万名的游客充当评判，评选出冠军演员。

S盒作为分组密码算法的惟一非线性部件，非线性性质是其区别于行移位、列混合等其他变换的决定因素.非线性度是用来刻画函数非线性性质的参数，对n元布尔函数，其非线性度Nf为[11]

Nf=2n-1(1-max|Sf(ω)|),0≤ω≤2n-1-1

(13)

对某(p,q)函数F，其非线性度为[12]

(14)

根据布尔函数的Walsh变换式(12)可对式(14)进行推导得

(15)

式(15)描述了布尔函数非线性度的计算方法.以DES算法第一个S盒为例，设其输出各位分别为y1,y2,y3,y4∈GF(2).根据式(10)、式(12)和式(15)，可以编程分别计算出DES算法第一个S盒输出各位的非线性度如表1所示.

表1 DES第一个S盒各位输出的非线性度

2.2 S盒输出位排序方法

引入“透明阶[12]”这一概念，对S盒的非线性性质与能量信息泄漏之间的关系进行推导.“透明阶”为Prouff等[12]提出，用来表示S盒抗能量攻击的能力：透明阶的值越大，能量信息泄漏程度越大，S盒抗能量攻击的能力越弱.

对一个(p,q)函数F，其透明阶τF定义为

(16)

式中：β为S盒输出连续的状态函数；H(β)为其汉明质量；DεF为函数F的线性结构.透明阶的下界公式如式(17).

(17)

又由式(13)可得

max|Sf(ω)|=1-21-nNf,0≤ω≤2n-1

(18)

根据式(18)对式(17)进行推导可得

(19)

进一步化简可得

(20)

由式(20)可知非线性度与透明阶之间存在正相关的关系：非线性度越大，透明阶越大；反之亦然.从侧信道泄漏角度来看，式(20)说明，S盒输出各位中非线性度大的比特位存在信息泄漏的概率更大.利用该结论可得到提高t检验效率的方法：先对S盒输出位的非线性度进行计算，而后按照非线性度由大到小的顺序对各输出位实施t检验.由于检测的目的在于确定是否能够检测出信息泄漏，而非准确地量化信息泄漏或得到信息泄漏的特征，因此当某一比特位检测出能量信息泄漏时t检验即可停止，而无需对剩余S盒输出位进行检验，当所有的检验位均通过t检验时方可判定不存在信息泄漏.

3 方法验证

本文以DES算法为例，在公开的DPA Contest V2(http://www.DPA Contest V2.org/)数据库中选择10 000条密钥为一固定值，明文为一组随机输入的DES加密算法的能量迹，对提出的排序方法进行实验验证.

3.1 验证基础

在对S盒的输出位实施t检验时，首先需要确定S盒输出时刻在DES算法的完整能量迹中的位置.本文采用主成分分析(principle component analysis,PCA)降维法对S盒输出时刻所对应的能量迹中的采样点位置进行确定[13-14]，DPA Contest V2数据库中对每条DES算法的能量迹设置了10 088个采样点，图1为利用10 000条能量迹进行PCA降维的分析图.

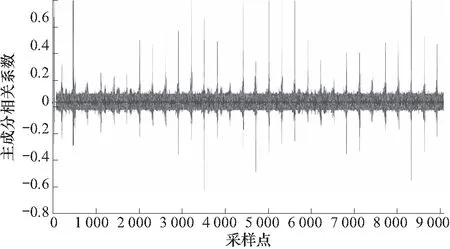
图1 PCA降维分析图Fig.1 PCA dimensionality reduction analysis diagram

图1中，横轴为能量迹中的采样点编号，纵轴为PCA降维的主成分相关系数，主成分相关系数的绝对值越大，采样点能耗中所含的信息量越大.

PCA降维结果中的特征维度与能量迹中的采样点一一对应，降维后通过矩阵逆映射的方法对含信息量较多的特征维度所对应的能量迹中的采样点位置进行确定，综合时间顺序和能耗大小两方面因素进行筛选可知，DES加密算法第一轮S盒输出时刻对应的是能量迹中的第314个采样点.

3.2 实验验证

首先对DES加密算法第一轮第一个S盒实施t检验.按照表1中得到的非线性度的大小顺序，利用所提出的排序方法实施t检验时的检验顺序应为y2→y3→y1→y4(yi表示S盒的第i位输出)，其中y1和y4的非线性度相等，检验顺序可调换.

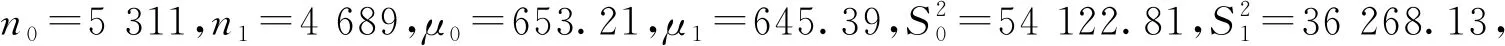
1.85<4.50

据此判断，第一个S盒的第二位输出不能检测出能量信息的泄漏.而后按照既定顺序，对S盒输出的第三位进行检验，计算得到t值为7.37>4.50，判定第三位输出能够检测出信息泄漏.至此t检验结束，结论为能够检测出能量信息的泄漏.

为与原方法进行比较，对S盒第一位输出进行检验，得到t值为2.79<4.50，判定第一位输出不能检测出能量信息泄漏；对第4位输出进行检验得到t值为8.32>4.50，能够检测出能量信息泄漏.

根据以上结果分析可知，在改进前从前至后逐位实施的t检验方法中，需要依次检验S盒输出的前3位才能检测出能量信息的泄漏，而按照本文所提出的方法则只需要检验第2位和第3位输出即可得出正确结论，可较原方法少进行一次t检验.为排除偶然性因素，随后对其余7个S盒分别进行了实验验证，具体验证过程不再赘述，实验结果汇总如表2.

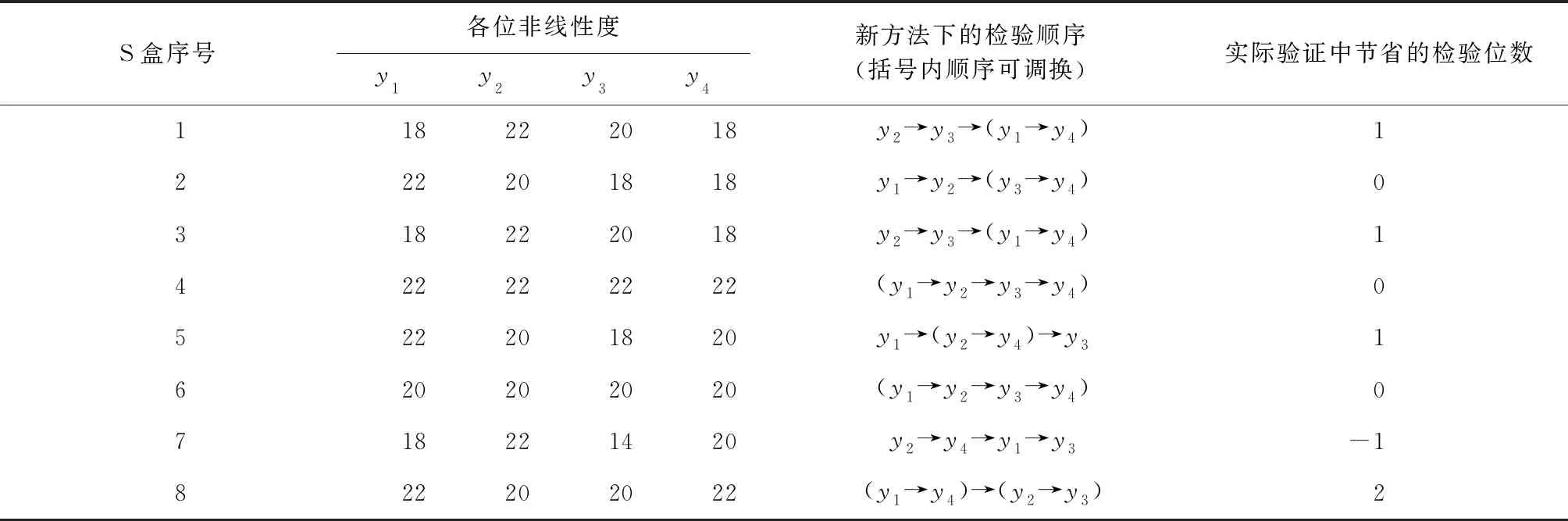
表2 DES加密第一轮各S盒输出位方法验证情况

表2中，“实际验证中节省的检验位数”指利用本文所提出的方法较原方法少实施的t检验次数，分析该指标可知在本文的验证实验中，利用新的排序方法令DES算法中半数的S盒不同程度地减少了检验次数，提升了检验效率.同时，对验证过程中出现的两种特殊情况分析如下.

(1) 第4个和第6个S盒各位输出的非线性度相同，新方法与原方法检验顺序相同，检验效率不能得到提升.需要说明的是本文提出的t检验位排序方法仅适用于S盒各输出位非线性度不同的情况，不适用于非线性度相同的情况.事实上，本文提出的排序方法可以“变相”地应用于这种情况：第4个S盒较第6个S盒输出位的非线性度大，因此可以先对第4个S盒实施检验.

(2) 在对第7个S盒实施t检验时，新方法较原方法的检验效率有所下降.需要说明的是本文所提出的排序方法是建立在信息泄漏“可能性”基础上的，因此在一定的检验阈值下，会出现泄漏可能性较大的检验位不能检测出泄漏而泄漏可能性较小的检验位能检测出泄漏的情况从而使检验效率下降.根据统计学原理分析可知，当检验量足够大时，这种情况出现的概率将大大减小.

总而言之，与原检验方法相比，本文提出的检验位排序方法可对存在能量信息泄漏概率大的t检验位先进行检验，从而能够减少检验次数，比原方法更快地检验出存在的能量信息泄漏，这在检验位数较多，检验情况较复杂，数据处理较繁琐的情况下可以显著提升检验效率，节省检验成本.

4 结束语

本文通过布尔函数的Walsh变换和非线性度对分组密码的S盒进行了研究，通过分析S盒输出位的非线性度与“透明阶”这一衡量能量信息泄漏参数的联系，得出了一种对分组密码的能量信息泄漏实施t检验时对S盒输出位进行排序的方法.验证的结果表明该方法能够有效提升t检验效率，节省检验资源.

由于时间等因素所限，本文仅对t检验检测分组密码能量信息泄漏的排序问题进行了研究，下一步可以对其他密码算法的t检验过程进行研究以构建更完善的t检验位排序方法体系.