弹丸连续挤进过程中身管坡膛受力和磨损分析

邹利波，于存贵，冯广斌，仲建林，刘宪福

(1.南京理工大学 机械工程与动力学院, 江苏，南京 210094；2.中国船舶重工集团第713研究所, 河南,郑州 450045)

火炮实弹射击过程中，身管是一个受力十分复杂的部件，在高温、高压、高速火药气体及弹带塑性变形体内压力急剧变化及弹带导转侧作用力的反复作用下，其身管内膛结构的形状、尺寸逐渐受到破坏. 坡膛是火炮身管中烧蚀、磨损最严重的部位，能引起火炮弹道性能和身管寿命的急剧变化. 在弹带挤入坡膛过程中，弹带材料首先被挤入带有锥度的坡膛，然后被膛线切割，弹带与身管内膛之间的接触压力很大，在挤进结束时，弹丸速度可达几十米每秒，弹带与管之间的摩擦具有高速高接触压力特性. 随着射弹发数的增加，坡膛受力的状态越发恶劣，磨损程度更加严重. 目前，对身管坡膛受力规律及磨损研究的报道较少. Bin Wu等[1-3]通过模拟实际发射过程中静态和动态的弹带挤进过程，研究了不同材料的弹带与身管之间的摩擦影响. 陆野等[4]建立了不同坡膛角度下考虑枪管和弹头结构特性等因素的三维有限元模型，研究了不同坡膛角度下挤进阻力随位移的关系. 孙全兆等[5]通过数据模拟研究了弹丸挤进坡膛时弹带的动态挤进过程，分析了弹带变形及刻槽形成过程，也为对坡膛在挤进过程的受力进行分析. 沈超等[6]建立了不同寿命阶段内膛损伤枪管的弹-枪热力耦合有限元模型，研究了弹头形貌损伤，未对枪管内膛损伤进行研究. Ding等[7]提出了一种磨损身管的有限元建模方法，同时研究了不同磨损程度的身管对弹丸挤进过程以及内弹道性能的影响.

综上所述，诸多学者对弹丸挤进身管过程进行了理论方面和数值计算方面进行了大量的研究，但是对身管坡膛结构的受力状态以及摩擦磨损状态研究的较少. 此外，建立的身管膛线有限元模型也未考虑膛线的工艺倒角，未考虑膛线倒角的弹炮耦合有限元模型在一定程度上与实际结果不符合. 因此，作者在前人研究的基础上，建立了考虑工艺倒角的坡膛结构有限元网格模型，同时建立了弹炮耦合热力学有限元模型. 模型中考虑了火药燃烧产生的温度和压力对挤进过程的影响；考虑弹带与身管之间摩擦因数随温度和压力的变化等. 详细的研究了弹带挤进坡膛过程中，坡膛受力规律以及连续射击环境下坡膛摩擦磨损规律.

1 弹炮耦合热力学有限元模型

1.1 有限元模型

以某中口径舰炮身管为研究对象，从完整身管中截取身管坡膛起始部结构(含坡膛锥度、带工艺倒角的阳线与阴线)，根据邹利波等[8]提出的线膛身管参数化建模方法，分别建立了该部分和弹丸的有限元网格模型，并采用C3D8RT和C3D6T单元对其划分网格. 在有限元模型中，弹带与弹体采用节点绑定的方式来模拟弹带与弹体的装配关系；弹带、弹体定心部与坡膛内表面接触设置；弹丸与装药作为刚体处理，装药质量以质量点的形式均匀耦合在弹丸内表面. 由于弹带切入膛线的过程中，弹带内部单元网格会暴露出来与坡膛内表面接触，故弹带采用自接触设置. 图1为身管坡膛起始部详细结构的有限元网格模型，图2为装配后的弹炮耦合有限元网格模型. 其中，身管坡膛结构网格模型单元个数为826 500，节点个数为726 785.

图1 坡膛结构有限元网格Fig.1 The finite element grid model of the forcing cone

图2 弹炮耦合有限元网格Fig.2 The FEM model of projectile-barrel interaction

1.2 材料模型

弹带材料为黄铜，身管材料为炮钢. 弹丸在挤进过程中经历弹塑性变形及损伤，最终发生局部化韧性断裂，涉及到弹带材料的应变硬化、应变率硬化和温度软化，Johnson-Cook适合描述大部分金属材料[9-10]，故采用Johnson-Cook本构模型及其失效本构模型，其表达式分别为

(1)

(2)

(3)

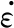
表1 弹带的Johnson-Cook材料模型参数Tab.1 Johnson-Cook material parameters of rotating band

表2 弹带和炮钢材料的热物理参数Tab.2 Thermo-physical parameters of gun steel and rotating band

1.3 边界条件与载荷

在火炮射击过程中，膛内火药燃气的强制对流作用，火药燃烧释放的热量穿过热边界层逐渐传递到身管，通过热传导不断将热量传递到外壁，外壁温度逐渐升高，之后，通过自然对流的方式，热量逐渐被环境气流带走. 膛内高温火药气体与膛壁之间存在温度差，因此必然发生热量交换. 由于舰炮连续射击过程中，射击间隔相对较短暂，故假设弹丸挤进前，坡膛表面已受到火药燃烧产生热量. 此时身管主要受到3部分热量：第一部分是火药气体以强迫对流换热的形式直接作用在坡膛表面的热量；第二部分是外壁面受到冷却水对流换热产生的热量；第三部分是弹带挤进膛线的过程中，由于塑性变形，不断出现的新生面与身管膛面剧烈摩擦，摩擦功最终表现为热量的释放.

① 初始条件为t=0，T=Ta，Ta为环境温度；

② 内、外边界条件(t>0)，身管内表面边界条件为

(4)

身管外表面边界条件为

(5)

式中：hg为火药气体与身管内表面的换热系数；he为周围空气与燃烧室本体外表面的对流换热系数；Te为环境温度. 弹丸发射过程中，火药气体沿身管轴向流动的方式是带热体的紊流流动，这种流动方式的显著特点是强烈的漩涡运动. 因而形成身管壁与火药气体热交换的主要形式为强迫对流换热，为简化求解问题，现假定只存在强迫对流换热，当求出放热系数后，再针对辐射换热作适当的修正. 火药燃气的放热系数根据相似理论计算：

Nu=f(L/d,Re,Pr)=

0.023Re0.8Pr0.4=h(z,t)d/Kg(t)

(6)

由式(6)可得：

(7)

式中：Re为雷诺数；Pr为普朗特数；Vg(t)、Kg(t)、ρg(t)、μg(t)、Cpg(t)分别为火药燃气的流速、导热系数、密度、动力粘度和比热；Kc为辐射修正系数

在本文的研究中，重力载荷作为常力直接加载在模型中，采用正装药的内弹道参数，按照弹底压力-时间曲线关系将压力施加在弹带后部所有作用面上，以模拟火药气体对弹丸的作用，如图3所示. 不考虑身管后坐对挤进过程的影响，同时不考虑弹丸卡膛过程，初始位置为弹带凸起与坡膛紧密接触开始模拟弹丸挤进过程.

图3 弹底压力与时间的曲线关系Fig.3 Curve relationship between bottom pressure and time

1.4 摩擦模型

在挤进过程中，弹带材料首先被挤入带有锥度的坡膛，然后被膛线切割，弹带与身管内膛之间的接触压力很大，在挤进结束时，弹丸速度可达几十米每秒，所以弹带与管之间的摩擦具有高速高接触压力特性. 采用Coulomb摩擦模型，如式(8)所示. 高温、高压和高速环境下，弹带与坡膛之间的摩擦因数是变化的，Matsuyma等[12]指出旋转弹带与身管之间的摩擦因数随材料的热物理性能、表面接触压力、弹带宽度和初始环境温度有关，其关系式如式(9)所示

f=uFn

(8)

(9)

式中：Hp为弹带的宽度；ap为弹带材料的热扩散系数；FP为弹带与坡膛之间的接触压力；V为滑移速度；Tm为弹带材料的熔点温度；T0为初始温度；λp为弹带材料的热传导系数. 在Abaqus商业软件中，弹带与坡膛之间的摩擦因数通过使用子程序VFRIC_COEF来实现.

1.5 磨损模型

磨损计算采用实际中广为认可的Archard模型[13-14]：

dV=KdFPdL/H

(10)

式中：dV为磨损体积；dFP为弹带与坡膛接触面的法向压力；dL为弹带与坡膛之间的切向滑移距离；H为炮钢材料的硬度；K为磨损因子.

dV，dFP和dL又可以用式(11)表示为

(11)

式中：dW为磨损深度；dA为接触面积；u为相对滑移速度；t为滑移时间.

将式(11)代入式(10)可以得出

(12)

其变形为

(13)

式(13)用于计算单个挤进过程的磨损量. 式中：Wij为j时刻i点出的磨损量；T，σij和uij可以由有限元模拟结果直接得到；n为1次模拟的总步数. 利用式(3)可以计算1次挤进坡膛的磨损量.

弹丸挤进身管过程中，坡膛结构摩擦磨损有限元模拟的基本假设：

① 由于单发射击后的坡膛磨损量较小，假设每一发弹丸挤进后，坡膛磨损后的轮廓变化不会对下一发弹丸挤进产生影响；

② 假设连续射击环境下，身管材料表面硬度保持恒定不变.

弹丸挤进身管过程中，坡膛结构摩擦磨损有限元模拟方法主要分为两步:①模拟弹丸挤进坡膛过程中弹带的滑动，从有限元模型中选取目标节点n，使用Python语言提取出计算磨损深度所需的第i次正法向压力σij和该节点的滑移速度uij，在Matlab中用式(13)计算每一次计算后的磨损深度;②将前一次模拟的结果的坡膛节点温度和残余应力作为下一次模拟的模型初始条件. 不考虑前一次磨损深度对下一次的影响，如此反复20次，将20次磨损量相加，即可得到弹丸挤进坡膛20次后，坡膛的目标位置的磨损量.

2 计算结果分析

通过数值仿真计算分别获得了舰炮身管在单发射击和连续20次射击环境下，身管坡膛的受力状态和磨损规律. 通过实弹射击试验回收的弹带变形图，与数值计算结果对比，数值计算获得的弹带变形图与回收的实弹的弹带变形情况基本一致，且弹带刻槽完成后的Miss等效应力约为430 MPa左右，在一定程度上说明建立的有限元模型具有一定的可信度.

图4 试验与数值计算后的弹带变形图Fig.4 Comparison of rotating band deformation after test and numerical calculation

2.1 坡膛受力规律分析

为了能够反映身管坡膛的受力规律，选取坡膛膛线起始处3个单元节点，分别为节点1、节点2、节点3和膛线起始处导转侧节点节点4和节点5，如图5所示.

图5 节点提取位置示意图Fig.5 Diagram of node extraction location

挤进过程中，弹带的塑性变形与挤压导致身管坡膛受到法向挤压作用力和弹-管之间切向作用力. 根据有限元计算，获得了挤进过程中，坡膛受到的挤压作用力和弹-管之间切向作用力，分别如图6和图7所示. 从图6曲线可以看出，坡膛受到的作用力呈现4个峰值，这是由于弹带的结构引起的. 其中，坡膛处节点1处的作用力峰值出现在第2个波峰，是由于前弹带第2个凸槽导致的，其法向挤压作用力大小约为5 045 N；坡膛处节点2处的作用力峰值出现在第1个波峰，是由于前弹带第1个凸槽导致的，其大小约为5 753 N；坡膛处节点3处的法向挤压作用力峰值出现在第4个波峰，是由于后弹带第2个凸槽导致的，其大小约为5 531 N；膛线导转侧处节点4处的法向挤压作用力峰值出现在第2个波峰，其大小约为2 448 N；节点5处的挤压作用力峰值出现在第2个波峰，其大小约为1 978 N. 从图7曲线可以看出，弹-管之间切向作用力与法向挤压作用力规律基本一致，身管坡膛处各个节点处的作用力大小分别约为405 N、460 N、447 N、200 N和192 N.

图6 单发射击时，弹-坡膛相互接触产生的作用力Fig.6 The force caused by contacting between the forcing cone and rotating band in a single shot

图7 单发射击时，弹-坡膛相互摩擦产生的作用力Fig.7 The force caused by friction stress between the forcing cone and rotating band in a single shot

经以上分析可以看出，坡膛处阳线受到的弹带法向挤压力约为5 400 N，受到的弹-管之间切向作用力约为400 N；膛线导转侧受到的挤压力约为2 400 N，受到的弹-管之间切向作用力约为200 N，身管坡膛处的阳线受力较膛线导转侧受力大. 图8和图9为挤进过程中身管坡膛结构在不同时间不同位置处的应力云图. 单发射击环境下，弹丸在火药燃气推力作用下挤进坡膛，在t=1.6 ms时刻，此时弹带尚未刻槽，弹带受到身管的挤压，发生弹塑性变形，身管坡膛应力约为536 MPa；连续射击20次，该处坡膛应力约为861.4 Mpa. 随着膛压的增大，弹带开始刻槽，并伴随着塑性损伤破坏. 在单发射击连续20次射击环境下，在挤进时刻t=1.65 s左右，身管坡膛应力分别约为818 MPa和1278 MPa；在挤进时刻t=2.2 ms左右，此时前、后弹带同时刻槽，身管坡膛应力分别为921.4 MPa和1 327 MPa. 在连续射击20发弹丸情况下，挤进时刻约为2.2 ms左右，身管坡膛应力达到了1 327 MPa. 单发射击和连续20发射击环境下，身管应力增加了24.5%. 弹丸挤进过程中，在同一时刻的同一位置，身管的应力增长随连续射击次数逐渐增加.

图8 单发射击环境下，身管坡膛Miss等效应力云图Fig.8 Stress cloud diagram of the forcing cone in single shot

图9 连续射击20发环境下，身管坡膛Miss等效应力云图Fig.9 Miss stress cloud diagram of the forcing cone in 20 consecutive firing shots

2.2 坡膛磨损规律分析

为了研究身管坡膛在弹带挤进过程的摩擦磨损情况，根据有限元计算结果，分别提取了膛线起始处节点1、节点2、节点3和膛线起始处导转侧节点节点4和节点5的接触应力、滑移速度，在Matlab软件中结合式(13)计算其磨损量，如表4所示.

表4 挤进过程中，身管坡膛磨损量Tab.4 Factors in the table

从表4中可以看出，单发射击环境或连续射击环境下，坡膛处节点3和膛线导转侧节点4的磨损量较大，分别达到了0.039 μm和0.037 μm，在相同射击环境下，身管坡膛不同位置的磨损量量不同. 连续20次射击时，坡膛上节点3的磨损量达到了0.052 μm，相对于单发射击环境下，该处的磨损量增加了约40%. 膛线导转侧节点5处在两种射击环境下的磨损量都相对较小，原因在于由于膛线是往左侧旋转，该侧受到的挤压和摩擦作用较小.

3 结论

建立精细化的弹炮耦合热力学有限元模型，考虑了含工艺倒角的膛线高精度有限元网格模型，数值计算了弹丸挤进坡膛过程中，坡膛的受力规律与坡膛磨损规律，得到以下结论：

① 通过数值仿真的弹带变形与试验回收获得的弹带实际变形对比，验证了所建立的高精度有限元模型具有一定的准确性；

② 身管坡膛的受力大小与规律与弹带的结构设计相关，不同的弹带结构设计导致坡膛受力的峰值大小与出现的时间不同，故合理的弹带结构设计是影响身管坡膛受力的一个重要因素；

③ 在单发和连续射击环境下，在阳线过渡处和导转受力侧的磨损量较大，且在随着射弹发射的增加，同一位置的磨损量增长较大，故合理的射击频率对身管磨损量有重要影响.

由于数值计算连续射击20发弹丸耗时太长，在将来的研究中，进一步优化有限元模型，提高计算效率，同时随着射击次数的增大，坡膛磨损量也相应的增大，在下一步的研究中，考虑磨损过程中网格的偏移以获得更加精确的计算结果.