电动汽车空调系统随机模型预测控制算法研究

管继富, 赵宇枫, 詹远, 曹立

(1.北京理工大学 机械与车辆学院 振动与噪声控制研究所,北京100081; 2.内蒙第一机械集团股份有限公司,内蒙古,包头 014032)

为减少对化石燃料的依赖和有害排放的产生,电动汽车有望在不久的将来获得重要的市场份额,目前,较短的续航里程是阻碍其发展的主要挑战之一. 空调系统是汽车中的重要辅助设备,用于维持车内温度舒适性,同时也消耗了车载电池的一部分电能,进一步缩短了电动汽车的续航里程. 因此,减少电动汽车空调系统的能量消耗成为当今一个重要的研究目标,采用合适的控制算法是提高空调系统效率的一个有效途径.

模型预测控制(MPC)是一种更为成功和更具前景的控制算法,被广泛应用于空调系统的控制,它具有多目标控制、约束处理、最优控制和抑制扰动等优点. 基于空调系统的动态模型,MPC算法可以预测系统未来的状态变化并提前制定最优控制变量,在满足约束条件的情况下最小化目标函数. 目标函数可以考虑多个因素,如空气温度,系统能耗,相对湿度,CO2浓度,磨损等[1-2]. 空调系统的主要功能是提供冷负荷以补偿车舱热负荷的持续变化,将车内温度维持在舒适的范围内. 在行驶过程中,热负荷会随着天气状况,人员数量,使用条件等因素而变化,给空调系统的控制带来了干扰变量. MPC算法能够对作用在空调系统上的热负荷干扰进行动力学建模,在计算控制变量期间预测扰动对系统的影响,并在优化策略中引入前馈变量加以抑制,这将使得MPC算法对热负荷干扰具有鲁棒性[3]. Aswani等[4]采用统计学方法估计出室内热负荷变化,并在MPC算法中补偿热负荷波动来减少空调系统的能量消耗. Oldewurtel和Dobbs[5-6]设计的MPC控制器中包含了因天气和环境变化而引起的热负荷扰动信息,实现了更节能的室内温度控制. He等[7-8]提出基于车速预测和乘客数量预测的随机MPC控制器分别用于电动汽车和电动公交车的空调系统,通过预测热负荷干扰以实现节能.

因此,本文针对电动汽车空调系统节能控制需求,提出了一种随机MPC算法. 首先,建立了空调系统制冷循环的动态模型和车舱热负荷模型,在建立空调系统控制模型时考虑了热负荷信息. 随后,设计了一个基本MPC算法用于参考对比,在基本MPC的基础上,采用马尔可夫链随机方法预测热负荷扰动,提出了随机MPC算法. MPC算法在实车上进行性能测试需要大量的成本、人力和时间,在实车测试之前可以通过仿真验证其性能,本文在Matlab/Simulink中对所提出随机MPC算法进行仿真验证.

1 空调系统控制模型

1.1 空调压缩制冷循环动态模型

图1是空调控制系统的能量流动图,包含车舱能量平衡和压缩制冷循环. 制冷剂在进入蒸发器之前为低温、低压的两相状态,在蒸发器中吸收热量后转变为过热蒸气. 随后,蒸气制冷剂被压缩为高温、高压蒸气,送入冷凝器中. 在冷凝器中制冷剂被冷却,历经两相状态,最终转变为高压液态制冷剂. 最后,高压液态制冷剂经膨胀阀节流,压力下降至蒸发器压力,转变为低压、低温两相状态,此为一个制冷循环. 压缩制冷循环的动态模型包含这4个主要部件的动力学.

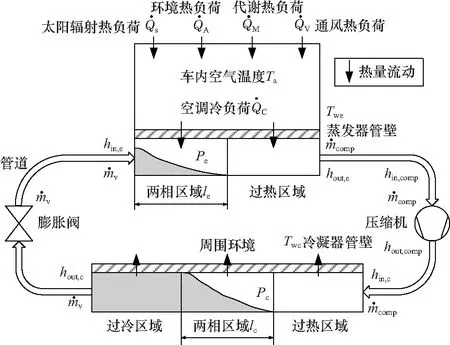
图1 空调控制系统能量流动图Fig.1 Energy flow diagram of air-conditioning control system

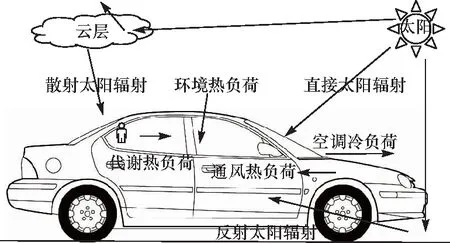
图2 电动汽车车舱热负荷构成Fig.2 Heat load of electric vehicle cabin room

压缩机和膨胀阀的动力学相比于热交换器要快上一个数量级,可以采用经验方程式对其进行建模[9]

(1)

hout,comp=ηis[his-hin,comp]+hin,comp

(2)

(3)

式(1)和式(2)分别描述的是通过压缩机的制冷剂质量流量和比焓变化,式(3)是通过膨胀阀的制冷剂质量流量. 公式中各变量的含义如表1中所示,例如hout,comp表示压缩机出口比焓.

依据制冷剂的状态,换热器可划分为过冷区域、两相区域和过热区域,如图1中所示. 两相区域的长度动态变化,并采用集总参数建模;应用质量守恒和能量守恒原则,换热器的动态模型为[9]

αieπDiele(Twe-Tre)

(4)

(5)

αieπDiele(Twe-Tre)-αieshπDie(Le-le)(Twe-Tre)

(6)

(7)

(8)

αicπDiclc(Twc-Trc)-αicshπDic(Lc-lc)×

(9)

式(4)描述的是蒸发器两相区域中制冷剂到蒸发器管壁的能量交换,式(5)是蒸发器管道中蒸气制冷剂的变化速率,式(6)是蒸发器管壁的能量平衡. 式(7)是换热器中的制冷剂质量,和蒸发器相似,式(8)是冷凝器管道中蒸气制冷剂的变化速率,式(9)是冷凝器管壁的能量平衡. 表1为参数说明列表.

蒸发器(冷凝器)空气侧换热系数αoe(αoc)与风扇转速Ne(Nc)相关,可以拟合为多项式函数[10]

(10)

表1 主要结构仿真材料参数

1.2 车舱热负荷模型

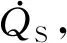
(11)

太阳辐射热负荷是由穿过车窗玻璃的辐射通量引起的,可以分为直射,散射和反射辐射热负荷3个部分

(12)

环境热负荷是环境空气通过外部对流、车身面板传导和内部对流这3个过程传递给车厢空气的热负荷,计算公式为[7,12]

(14)

代谢热负荷的释放是由一系列复杂的化学变化引起,一般采用经验公式计算[11]

(15)

通风系统用于维持所需的室内空气质量,同时也伴随热量的交换,计算公式为[7]

(16)

空调冷负荷计算公式为

(17)

1.3 控制模型

如图1所示,空调系统蒸发器吸收车舱获得的热负荷,将车内温度维持在舒适的范围内. 将车内空气温度Ta,蒸发器压力Pe,蒸发器两相长度le,蒸发器管壁等效温度Twe,冷凝器压力Pc以及冷凝器管壁等效温度Twc选取为整个系统的状态变量,控制模型的状态向量为

X=[lePeTwePcTwcTa]

(18)

系统的输入为压缩机转速Ncomp,蒸发器风扇频率Ne,冷凝器风扇频率Nc,控制输入向量为

U=[NcompNeNc]

(19)

控制模型的输出为车内空气温度Ta,综合式(1)～式(17),可将控制模型改写成状态空间表达形式

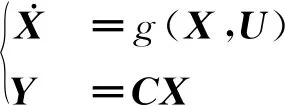
(20)

2 模型预测控制算法

MPC算法适用于复杂多变量过程的高性能控制,包括3个步骤[13]:① 根据预测模型,权重和约束条件,构建一个有限时域内的最优控制问题,此步骤称为预测. ② 实际上,最优控制问题求解的结果是一组最佳控制序列,只有最优控制序列中的第一个元素,也就是当前时刻的控制动作,被施加到系统;序列中其余的元素,也就是未来时刻的控制动作,都被抛弃;在下一个时刻,将基于新的初始状态求解一个向后推移的有限时域最优控制问题,该步骤称为滚动优化控制. ③ 由于在每个时刻的控制输入取决于当前的测量(估计)状态,这相当于提供了一个反馈校正步骤.

式(20)中的控制模型为高度复杂的非线性模型,难以用于设计实时MPC控制算法. 线性MPC可以解决这一问题,在稳态工作点时,车舱热负荷为定值,其线性离散化模型为

u=A(x0,u0)x+B(x0,u0)u

(21)

(22)

式中：x0和u0分别为状态向量和控制输入向量在稳态工作点的值；x和u分别为与x0和u0的较小动态偏差.

2.1 基本模型预测控制算法

为了验证所提出控制算法的有效性,设计一个基本MPC算法作为参考对比. 空调系统的控制问题是一个典型的跟踪问题,系统的输出变量Ta被期望尽可能地接近设定值,且消耗最小的能量,MPC的结构如图3所示. 在每个采样时刻,有限时域优化问题的目标函数为

uT(k)Ruu(k)+ΔuT(k)RΔuΔu(k)]

s.t.

(23)

式中:N为预测范围；u为待优化的控制变量;e(k)为系统输出和输出参考的差值;e(k)=y(k)-r(k).

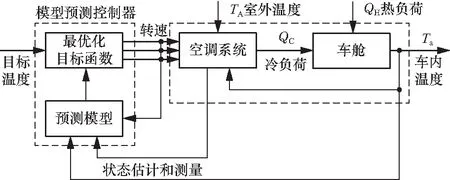
图3 空调系统模型预测控制算法结构图Fig.3 Structure diagram of air-conditioning system MPC algorithm

2.2 随机模型预测控制算法

汽车的行驶速度可以建模为马尔科夫随机过程ω(·),ω(k)∈W,k∈0+;生成ω的随机过程被建模为具有状态集合W={ω1,ω2,…,ωs}的马尔可夫链,对于所有的i∈{1,2,…,s},ωi∈W[14]. 状态之间的演变由转移概率矩阵T∈s×s决定,当前状态只与上一时刻状态相关[15]. 在任意时刻k,当前时刻的车速ω(k)可以测量,下一时刻的车速ω(k+1)的概率分布使用转移概率矩阵T预测,计算公式为[16]

Pr[ω(k+1)=ωj|ω(k)=ωi]=[Tij] (24)

本文使用最大似然法选取k+1时刻车速,将热负荷干扰作为系统的测量输入v(k),并作为状态的增广,随机MPC算法的预测模型如式(25)和式(26)所示,可以为该预测模型构建一个相似的最优控制问题.

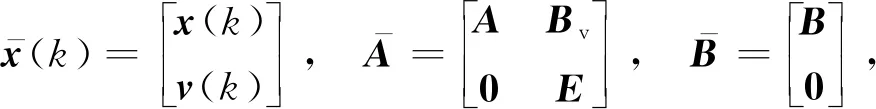
(25)

(26)

3 仿真结果和分析

环境状况和车速是影响车舱热负荷的重要因素,图4为一个晴天的每小时天气数据,包含太阳辐射强度和环境温度,最大太阳辐射强度对应的环境数据用于仿真模拟,为860 W/m2,环境温度为35 ℃. 图5中的SC03(speed correction driving schedule)循环工况是美国整车试验工况中的一个补充工况,用于测试空调使用对汽车性能的影响,时长600 s,平均车速9.7 m/s,最高车速24.5 m/s,本文选用该循环工况测试电动汽车空调系统在两种控制算法下的能耗表现. 图6为在上述环境条件和车速下的热负荷变化曲线,和图5对比可知,汽车的行驶速度对车舱热负荷有着显著影响,因此本文所提出的随机MPC算法通过预测车速对热负荷进行预测.

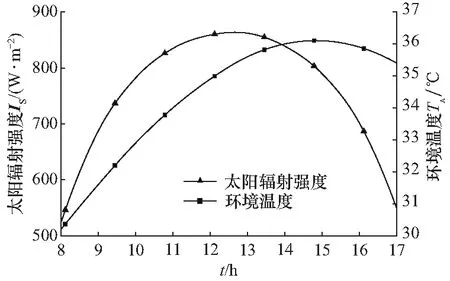
图4 太阳辐射强度和环境温度数据Fig.4 Weather data on solar radiation and ambient temperature

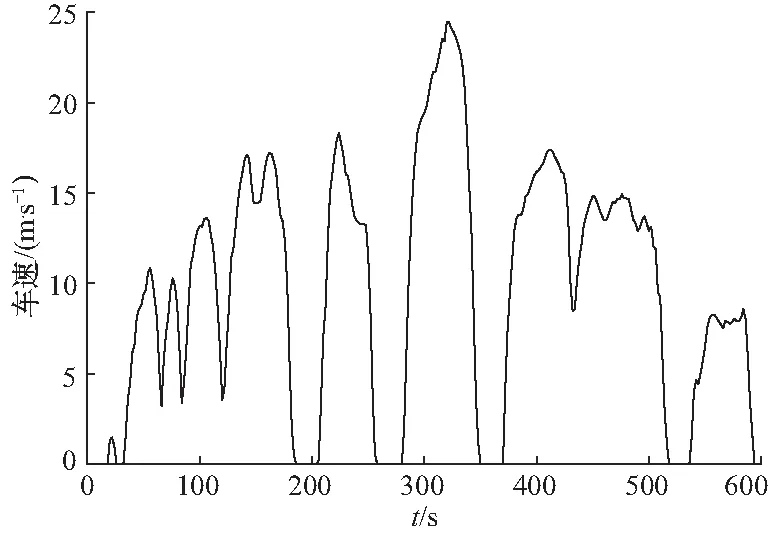
图5 SC03循环驾驶工况的速度曲线Fig.5 Vehicle speed of SC03 driving cycle

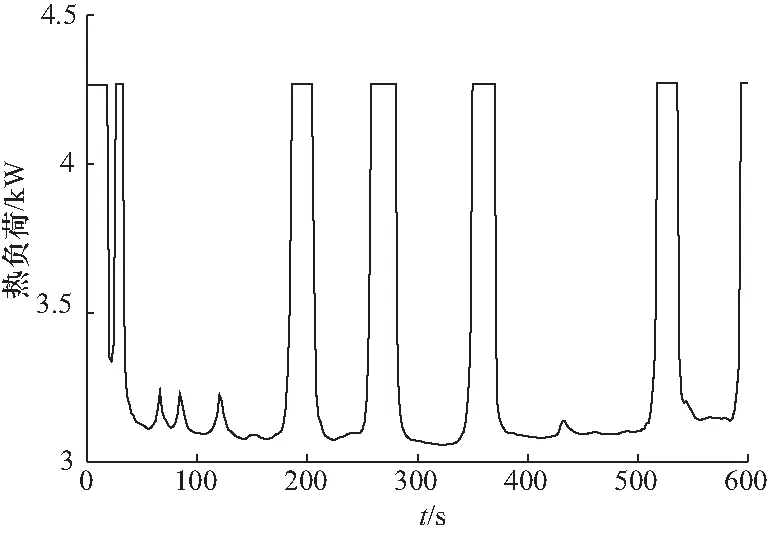
图6 SC03工况下的热负荷曲线Fig.6 Heat load curve under SC03 driving cycle

表2是本文MPC控制器的参数. 一个较大的输出权重用于保证温度控制性能；控制权重的选取用于尽可能降低压缩机转速,保证能量效率；较大的控制增量权重增加系统鲁棒性；较大的终端权重带来更好的闭环稳定性[9]. 压缩机和风扇转速的取值范围也如表1中所示. 车内初始温度为35 ℃.

图7是基本MPC算法和随机MPC算法的温度仿真结果,图8是控制输入. 从图中可以看出,随机MPC的温度控制性能要优于基本MPC,将温度维持在更小区间内. 当热负荷增加时(例如350 s),随机MPC的温度升高低于基本MPC,因为随机MPC能预测热负荷干扰的增加,更早地将压缩机和蒸发器转速升高. 同样,当热负荷下降时(例如370 s),随机MPC的过冷低于基本MPC,因为随机MPC将压缩机转速迅速降至一个较低值,以提供与当前热负荷相对应的低冷却负荷; 相反,基本MPC无法将空调系统的冷却负荷及时降低到适当的低值,恢复到目标温度的时间也要长于随机MPC. 图9是整个仿真过程中随机MPC和基本MPC的能量消耗曲线. 随机MPC算法的预测模型中包含当前和未来时刻的热负荷信息,在优化控制变量时,可预测热负荷干扰对控制系统状态和输出的影响,能更优地调节压缩机和蒸发器的转速以适应热负荷的变化；因此,在整个仿真期间内,随机MPC的能耗都低于基本MPC. 如表3所示,相比于基本MPC算法,随机MPC算法能够节约10%的能量. 综上,随机MPC算法有效提高了空调系统的温度控制性能并且减少了能量消耗.

表2 MPC控制器的参数

图7 基本MPC和随机MPC的温度曲线Fig.7 Temperature curve of basic MPC and SMPC

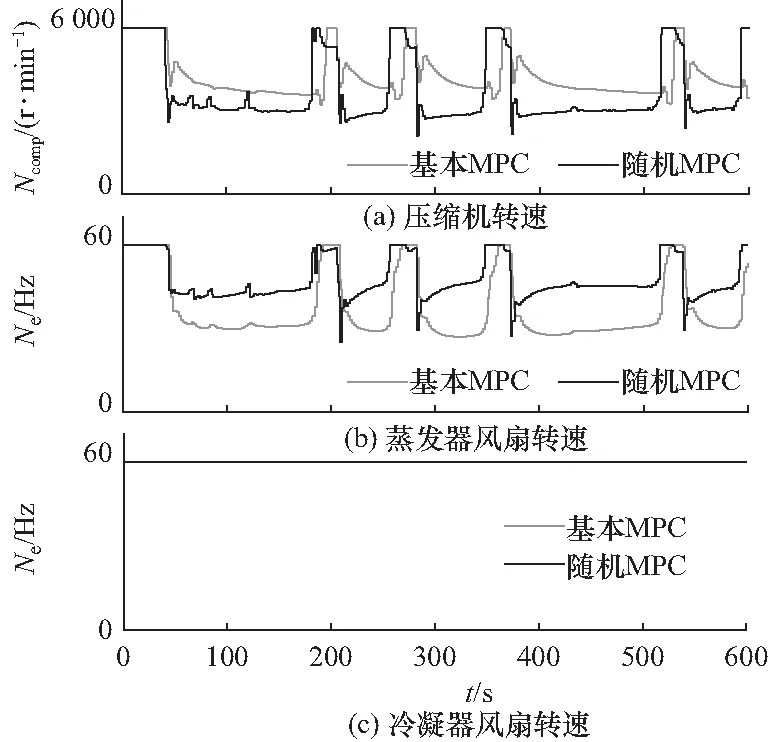
图8 基本MPC和随机MPC算法的控制输入Fig.8 Inputs of basic MPC and SMPC algorithms

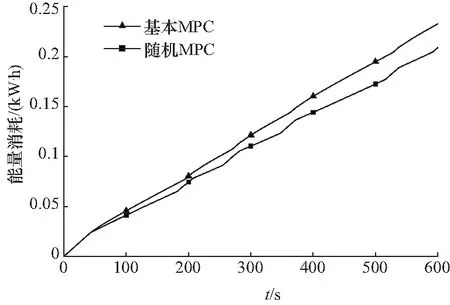
图9 基本MPC和随机MPC算法的能量消耗Fig.9 Energy consumption of basic MPC and SMPC algorithms

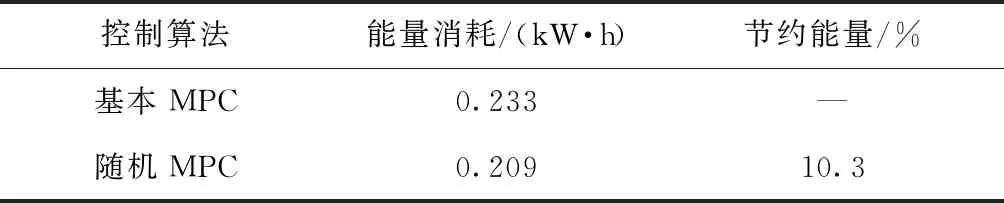
表3 随机MPC和基本MPC算法的能量消耗

4 结 论

本文基于移动边界和集总参数方法,建立了空调系统制冷循环和车舱热负荷模型,在控制模型中考虑了车舱热负荷信息. 随后,采用马尔可夫链随机方法预测汽车行驶速度实现车舱热负荷预测,提出了随机模型预测控制算法. 仿真结果表明,通过预测热负荷扰动,随机模型预测控制算法提高了空调系统的温度控制性能和能量效率,在仿真条件下节省约10%的能量. 仿真模拟是研究控制算法的重要手段之一,但和真实系统存在一定偏差,后续需对文中的控制算法进行实验验证.