用于增材制造的点云直接分层算法

杨 通，姚 山，薛凯华

(大连理工大学 材料科学与工程学院，辽宁 大连 116023)

1 问题的提出

增材制造(也称3D打印)由三维模型分层得到的切片数据直接驱动。随着三维扫描使用成本的降低，点云直接分层因可避免网格重建和修复等耗时过程[1]而渐受关注，然而由于缺少拓扑信息，点云分层的效率和容错性仍然远不及传统的网格分层[2]。

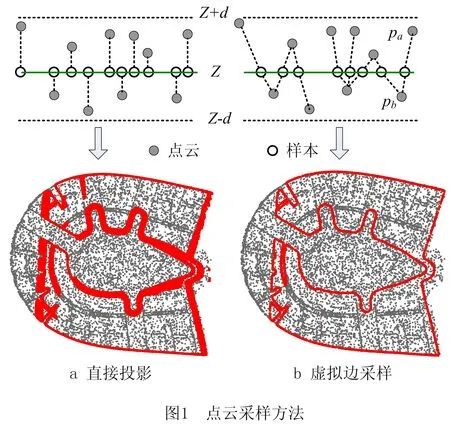
点云分层大多遵循“点投影到分层平面—曲线重建”两步计算的范式[3-4]。对于单个分层平面，首先将其附近的三维点垂直投影，获得二维带状样本(如图1a)，然后用样本逐层构造曲线。Javidrad等[5]采用自顶向下的方式对样本迭代精简后识别出关键点，由此拟合样条曲线；Chen等[6]则利用动态估算的曲率引导种子线段沿样本推进，自底向上构造多边形。这类早期工作主要关注曲线误差，仅重建光滑曲线或单条曲线。Xu等[7]以平面投影所得样本的轮廓作为初始估计并检测多条曲线，然后迭代更新轮廓顶点得到最终多义线。点投影操作后，点云分层归约为曲线重建这一欠定问题，对于曲线重建问题，基于Delaunay/Voronoi的算法族是第一个被严格证明的方法[8]。虽然多条线、离群点、稀疏/非均匀样本、尖角等复杂情形的重建能力[9-10]不断增强，但是投影导致的样本厚度不均匀给成百上千层曲线的自动重建带来挑战。用局部拟合的二次曲面代替平面进行投影可改善样本的均匀性[11]，也可以采用虚拟边与分层平面求交生成减薄的样本[12](如图1b)，其均匀性优于平面投影方法。虚拟边采样法还可与平面直接投影法混合使用来平衡采样密度和精度[13]。

另一类方法将点云像素化后在图像空间构造曲线[14]。程效军等[15]将投影后的样本转为二值图，抽取形态学骨架并拟合样条；Percoco等[16]用遗传算法生成非空像素的最短遍历路径；Huang等[17]通过Marching Square获得初始多边形，然后用拉普拉斯算子消除褶皱。图像类方法须谨慎确定像素尺寸，以平衡计算负荷和曲线的精度。为提高精度，可将分层平面与点云的移动最小二乘(Moving Least Square, MLS)曲面求交，得到隐式的交线[18]。基于MLS的扩展方法用Reeb图将点云沿分层方向分割为若干拓扑不变的区间，然后分别分层[19],解决了隐式曲线的拓扑结构在相邻层发生突变的问题。MLS方法因隐式曲面和曲线固有的平滑性而具有一定容噪能力，但未对尖角的重建效果进行检验。

Yaman等[20]和Minetto等[21]分别报道了立体光刻(Stereolithography, STL)网格模型的增量分层算法，他们都利用了连续层片在多数情况下拓扑同胚只发生轻微几何变化的特性，将分层平面自底向上扫过模型时，算法依据网格邻接关系更新已有曲线的坐标，并由网格拓扑变化事件更改曲线连接关系，避免重头构建每层曲线。虽然这类算法因依赖网格拓扑信息而无法用于点云分层，但是受相邻层形状相似性的启发，本文提出一种点云增量分层方法。首先通过虚拟边采样法[12]准备分层平面上的二维样本点，然后采用所提非监督神经网络按增量方式逐层学习样本的局部主成分，并建立其多义线表达作为输出。该网络称为竞争型主成分分析(Competitive Principal Components Analysis, CPCA)模型，其参照成长型单元结构(Growing Cell Structures, GCS)[22]，但重新设计了边的增长/删除、顶点移动、拓扑改变、属性更新等机制，以便利用层间相似性快速重建和跟踪成百上千层曲线。

2 点云分层算法

2.1 生成样本点

如图1所示为生成用于单层曲线重建样本点的常用方法，其中较稀疏的点为密度降低到5%后的原始点云，密集分布的点为得到的样本。直接投影法在截面拓扑结构复杂时会导致相邻曲线无法分辨，虚拟边采样法可生成厚度均匀且拓扑结构可分辨的样本[12]，因此本文采用后者。虚拟边采样法在当前分层平面Z附近(距离小于d)随机查找上下最近邻点对[pa,pb]，连接两点的线段记为虚拟边ea,b，若ea,b与Z相交，则交点为一个有效样本[12]。为提高样本密度，当交点不存在时，本文继续依次查询pa的2～4近邻点pc；若ea,c与Z相交于点p且‖pa-p‖<3‖pa-pb‖，则认为该交点也是一个有效样本。

2.2 竞争型主成分分析网络模型

CPCA是一个动态变化的无向图。顶点集V中每个成员vi保存坐标wi，边集E={ei,j(θ)=(wi+wj)/2+θ(wi-wj)/2|θ∈[-1,1]}表示首尾顺序连接的线段，构成数条多义线。任意顶点最多有两条边。网络初始化为一个随机的三角形，然后从依次输入的样本中学习并更新网络属性，根据网络属性动态添加或删除边和顶点。给定当前输入样本p，其到边的距离

(1)

使式(1)取下确界的θ称为点到边的投影φ(p,ei,j)，边上对应的点为投影点PP(p,ei,j)，投影点到样本的向量为误差向量EV(p,ei,j)。为确定样本与边的对应关系，令边的感受野

Ai,j={p|D(p,ei,j)≤D(p,ex,y),∀ex,y∈E}。

(2)

网络目标函数衡量样本到边的总偏差为

(3)

其与最优输运曲线重建算法[10]中的Wasserstein误差法向分量相同，取最优值时任意边需满足

(4)

即边重合于感受野内样本所确定的主轴

(5)

(6)

两个特征值分别称为样本的信号和噪声。误差最优条件可简要描述为：任意顶点坐标等于其所在两条边的主轴的交点。

边用于表达其感受野内的样本，学习时不断向主轴移动以减小误差，添加新边也可以减小误差。为确定何时及如何增长边，需判定感受野内是否包含更精细的子结构，因此将其细分为左(L)、右(R)、上(T)、下(B)4个子感受野，如图2所示。任意顶点也定义了感受野Ai，等于所在边的感受野的并集。每条边最终都与7个感受野关联，即

Gi,j={Ai,j,Li,j,Ri,j,Ti,j,Bi,j,Ai,Aj}。

(7)

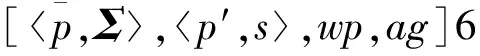
g={a,l,r,t,b,ai,aj}。

(8)

后文约定，当X表示某感受野时，x表示其对应的主轴。所有主轴默认的θ的范围为[-1，1]，也可用x([θ1,θ2])的形式显示指定为其他范围。因主轴和边都代表线段，在式(1)及其导出的投影、误差向量等函数中可相互替换使用。

感受野定义的6个属性需要在学习过程中更新。为此，网络找到当前样本的最近边em,n，更新覆盖该样本的感受野F(p)={A,L,T,Am,An}∈Gm,n的所有属性。高斯参数可按如下随机梯度下降法[23]更新：

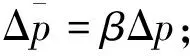
ΔΣ=β[Δp(Δp)T-Σ]。

(9)

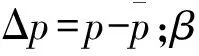
(10)

式中：s的初始值取0；p′为该感受野上一次收到的样本，在每个学习周期后更新为当前样本。感受野后两个属性wp和ag分别称作获胜概率和年龄，用于控制边的增长、删除和移动，初值也取0。

2.3 主轴竞争与边增长

em,n及其7个主轴可划分为5组，即祖父单元[am,an]、父单元a和e、子单元[l,r]和[t,b]，每一组均可表达局部样本的分布，获胜概率衡量哪一种表达方式误差较小。当前样本通过比较自身到不同单元的距离来估算F(p)每个成员X的获胜概率：

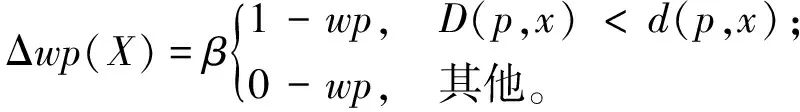
(11)

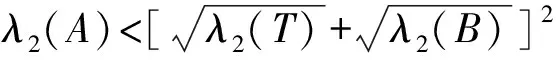
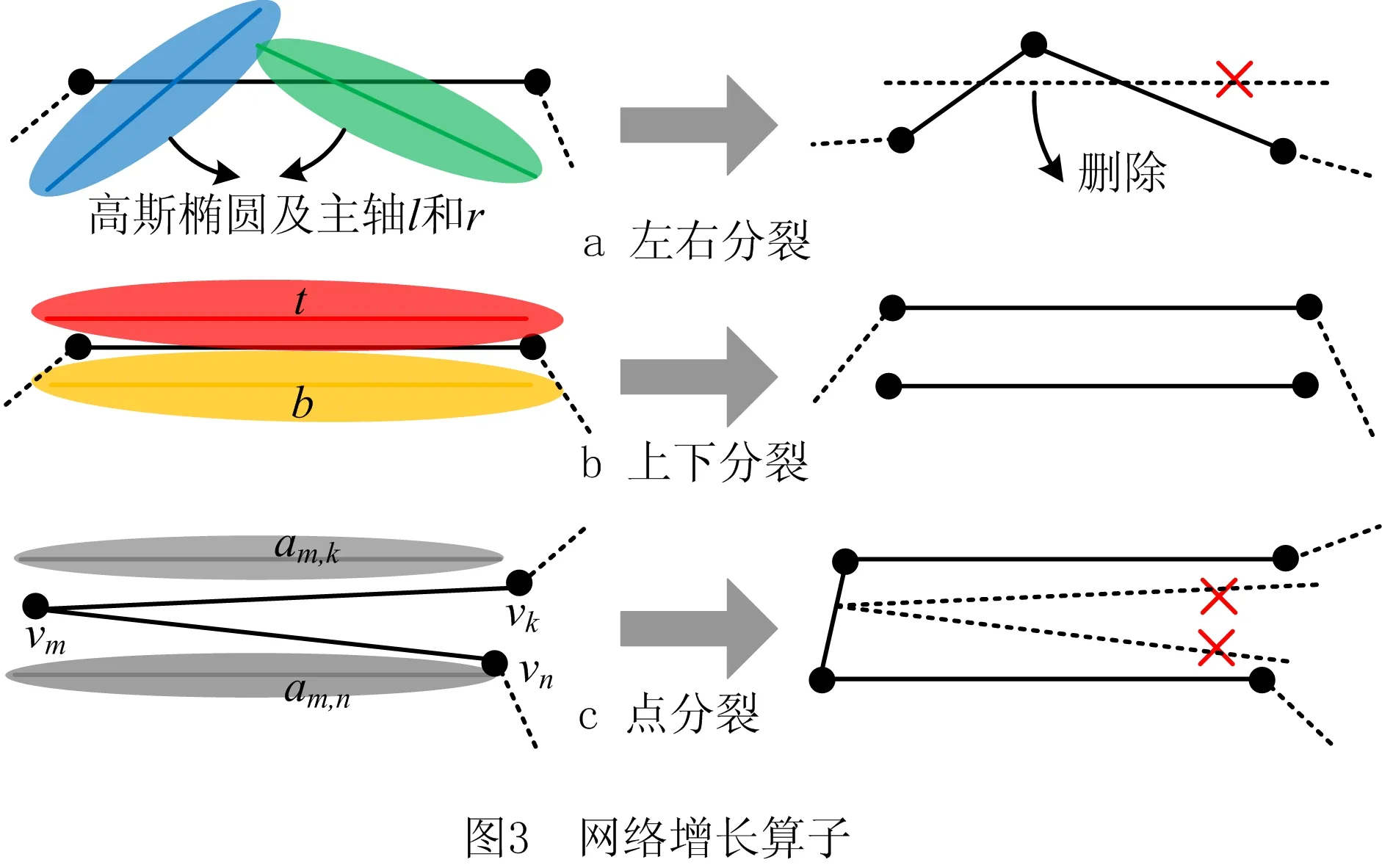
据上述分析，当min[wp(L),wp(R)]-s(A)>50%且大于两祖父单元感受野的获胜概率时，应触发左右分裂。同理，T和B满足该条件时执行上下分裂。偏置s(A)抑制样本稀疏区域增长边。当样本分布较复杂时，增长条件成立的可能性低，因此引入图3c中的点分裂，将顶点投影到两个相邻边的主轴以产生新边。2.2节得出理想顶点应重合于所在边的主轴交点，因此若两主轴所在直线的交点与顶点vm的距离d始终较大，则表明局部区域欠拟合或过拟合。由图3c可知，欠拟合时主轴比彼此约束的边更贴近样本，故获胜概率会超过50%，而过拟合会产生较大的wp(Am)。欠拟合区别于过拟合的另一特点是噪声λ2(Am)大于两主轴噪声之和(记为∑λ)。由以上分析可知欠拟合的特征如下：

d2>λ2(Am)>∑λ；

wp(Am,n)>50%>wp(Am)+2s(Am,n)。

(12)

为避免统计的不确定性，仅当式(12)在多次学习中持续成立才分裂vm，用ag(Am)记录该持续性。若式(12)成立，则将ag(Am)增加β(1-ag)，否则重置为0，当ag(Am)>50%时触发点分裂。

2.4 顶点的移动和删除

CPCA采用Winner-Take-All原则移动当前样本最近边em,n的顶点vm。式(4)给出误差随机梯度下降的方向为va=EV(p,e)。为抑制随机性，当该方向使边向获胜概率大于50%的主轴靠近时才移动vm。可表达边的全体样本的主轴包括a及其两个祖父单元，对于三者中的每一个x，边向其靠近的方向为vb(x)=EV[PP(p,x),e]。通过va和vb的夹角可以调节移动量，将3个主轴的贡献加权求和得到总移动量：

(13)

f(u,v)=

(14)

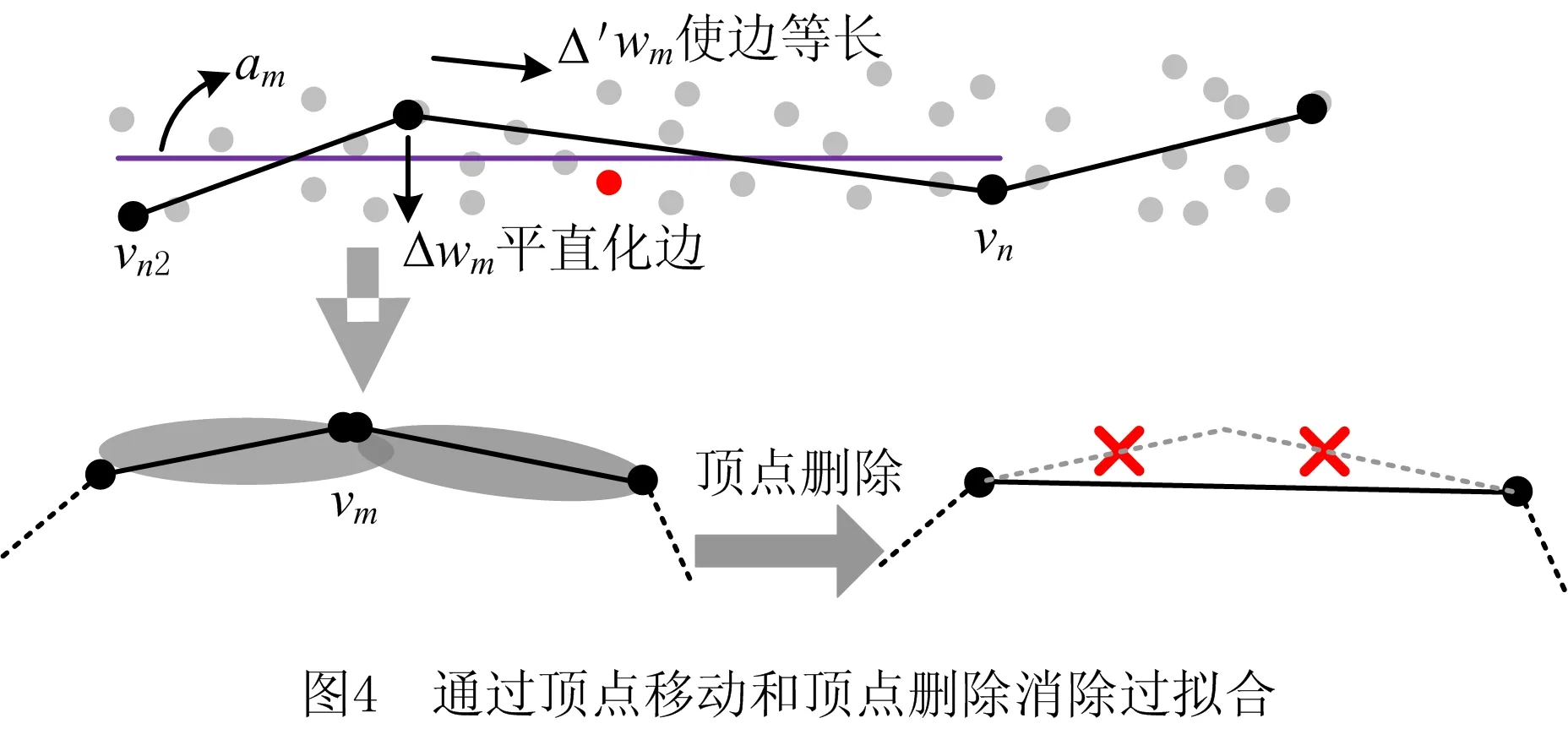
式中截断函数Ω(y)在y>0时取y，否则取0。式(13)表明：某主轴频繁获胜时，会使边迅速与其对齐；无过拟合时祖父单元的贡献量为0，满足误差最优条件后wp(A)≈50%且vb(a)≈0，因此顶点仅在σ2|σ→0范围内震荡。如图4所示，过拟合时，祖父单元贡献的移动使顶点所在的两边趋于平直，为进一步消除褶皱，可按GCS网络策略沿vc=p-wm方向移动[22]，从而产生等长边。与Δwm类似，为抑制随机性，需确认该方向趋于减小两边的长度差。为此，查找当前样本次近邻边em2,n2。当m=m2时得到长度差减小的方向vd=EV[(wn2+wn)/2，am，n]，由此导出另一移动分量

(15)

当m≠m2时，该式为0。

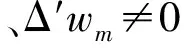
2.5 边竞争与拓扑变化

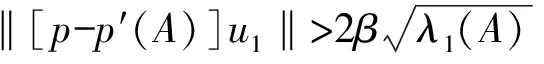
Δag=[s(L)-1]ag。

(16)

否则所有边的ag(A)增加[1-s(Lm,n)]/|E|，除数为总边数。上述不等式条件成立的概率与边长无关。

若当前样本到最近和次近边的距离差值d较小，则其中一边可能是冗余边[24]，用[ag(L)，ag(R)]估计该可能性。此时样本到边的距离已不能有效判定样本归属，因此认为两边中使夹角p′(A)-p,e取较小值的边与样本分布更一致，另一边记为ei,j。若ei,j的样本稀疏性较显著且前述d值较小，即则将左感受野的年龄ag(Li,j)增加

Δag=β(1-ag)，

(17)

否则将ag(Lm,n)降低β×ag(Lm,n)。左右感受野及边感受野的年龄之和称为边的年龄，记作

age(e)=ag(A)+ag(L)+ag(R)。

(18)

age(e)综合考虑了边在全局范围(第1项)和局部范围(后两项)的比较结果，代表边的有效性，age(e)>1表示e为无效边。对于CPCA的任意顶点，若其所有邻边均无效，则执行图4中的顶点删除算子。

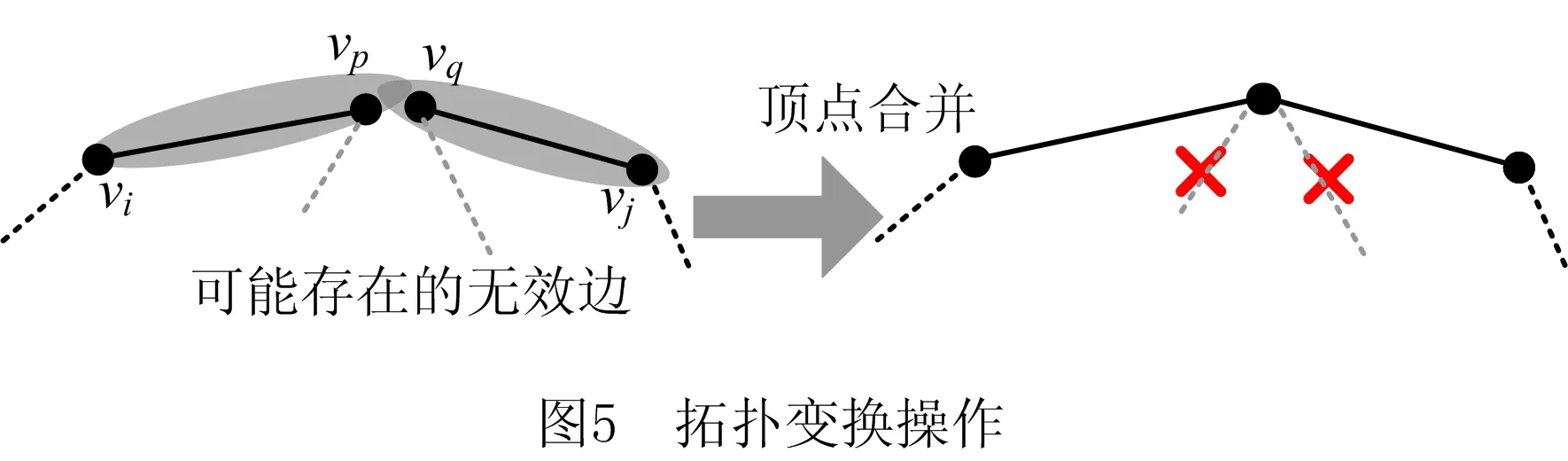
顶点被删除后不改变多义线的拓扑结构，然而CPCA还需跟踪不同分层平面上的拓扑变化。2.2节表明，理想顶点应与两邻边主轴的交点重合，与此相反，若非拓扑邻边的主轴相交，则可能存在拓扑错误，由此导出图5中的顶点合并算子。与CHL(competitive Hebbian learning)规则[23]一样，合并的两顶点为当前样本的最近和次近顶点[vp,vq]，本文在CHL基础上添加了两条约束。首先，两顶点各自均仅存在一条有效边(age<1)，记作ep,i和eq,j；其次，这两边的主轴近似相交。令d为ap,i([0,1+s(Ap,i)])与aq,j([0,1+s(Aq,j)])间的最短距离，当d2≤2λ2(Ap,i)时认为近似相交。用s扩展主轴参数范围以处理较稀疏的样本，用距离阈值代替相交条件可辨别两边共线的特殊情形，这两个条件成立时便可合并当前样本的最近和次近顶点，合并后的新顶点位于与两主轴距离之和最近的位置。

2.6 分层计算流程

将各计算过程组合得到点云分层流程：

输入：点云P。

输出：各层上的多义线。

步骤1初始化分层面Z和CPCA(为随机三角形)。

步骤2准备一个样本点作为CPCA输入(2.1节)。

步骤3通过边竞争(2.5节)和主轴竞争(2.3节)更新属性。

步骤4根据属性触发边增长/删除/拓扑变换算子。

步骤5移动顶点(2.4节)。

步骤6边平均学习次数n=n+1/|E|，若其比上次检查时的增量达到10次，则检查网络是否收敛，是则输出当前层多义线，并将Z移动到下一层。

步骤7迭代步骤2～步骤6，直到Z超过结束位置。

步骤8按Z倒序逐层检查并修复可能的拓扑错误。

步骤6中，网络收敛需满足3个条件：①多义线数量在[n-20，n]时间段内始终恒定；②边数量在该时间段内的变化率小于β；③所有边的噪声λ2(A)的平均值在连续3次收敛检查时的变化率小于β。当前层收敛后，CPCA不重置网络结构，直接切换到下一层继续学习，因此避免了从头构建下一层多义线。

由于统计学习具有随机性，无法保证成百上千层多义线中无任何拓扑错误，因此用步骤8按照Z倒序逐层检查。检查过程中，若某层存在开线或无效边(age>1)，则用下一层(Z+层厚)结果重新初始化CPCA并学习，直至收敛。若收敛后所得封闭线数量减开线数量比正向分层时大，则替换原有结果。

步骤2中计算虚拟边需查询最近邻点对，步骤3需查询当前样本的最近和次近边及顶点，算法采用可动态扩展/收缩的均匀网格[25]保存边、顶点及分层平面附近的点云，以加快查询速度。由于相邻层形状具有相似性，网格在分层平面移动时不用频繁地扩展或收缩。

3 实验结果与分析

为评价分层效率及多义线重建的几何误差和拓扑错误，将本文算法与基于平面最小二乘投影(Planar Least-Squares Projection, PLSP)的分层算法[7]进行比较。PLSP采用图1中的直接投影法准备样本，然后用滚球法抽取其外轮廓，最后迭代移动轮廓顶点，以最小化样本到顶点的加权距离和。与PLSP不同，本文目标函数衡量样本到边的距离和，类似于最优输运(Optimal Transport, OT)[10]曲线重建算法。OT算法从样本点的Delaunay剖分开始，不断合并对误差贡献较小的边，同时移动顶点以得到多义线。OT代表常用的基于Delaunay剖分的曲线重建算法族，因此也作为对比算法，其样本同样用虚拟边方法生成。所有算法都采用C++实现，其中PLSP的实现来自文献[7]，OT来自开源程序[10]，所有实验运行环境为Intel(R)Core(TM)i7-4790 CPU@ 3.6 GHz。为测试容噪性，在理想曲线上采样无偏差样本后，按高斯分布N(0，kε2)作随机移动，其中k控制噪声幅度，ε为最近邻样本点对的平均距离。用理想曲线C(θ)和重建多义线间的偏差衡量重建误差，每条边的误差按其感受野内曲线与边的Hausdorff距离计算：

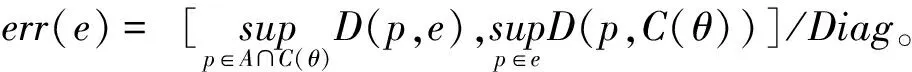
式中Diag为整体样本外包围盒对角线的长度。计算误差统计值时采用手动删除拓扑错误，并用试错法优选对比算法的运行参数。

首先用不同噪声幅度k及不同分布的4组样本测试CPCA的基本特性，得到如图6～图9所示的结果。所有图中都列出了CSR，OT，PLSP 3种算法的对比输出，图中的数字标号表示局部放大区，用于观察散乱分布的样本与重建曲线的拟合情况。图6和图7分别表示样条曲线和组合曲线两种典型的应用场景。在图6算例中，曲线既包含细长的尖角，也包含光顺区域，样本含10 000个点，噪声k=2，6；在图7算例中，样本有两个汉字，各采样7 000点，k=2，4。图6和图7表明：①当样本噪声较小时，CPCA输出逼近目标曲线的高精度多义线，曲线的光顺部分和尖角部分均得到重建；②CPCA和OT的尖角重建效果优于PLSP，这是因为前两者的目标函数优化样本到边的距离，而PLSP优化样本到顶点的距离，所以PLSP重建具有尖角特征的曲线时误差较大(如表1)；③噪声增加时，CPCA的输出由精变粗，精度随之下降，该特性与图6c～图6d中OT的重建结果表现一致，但OT为避免拓扑错误而生成了更简化的多义线。

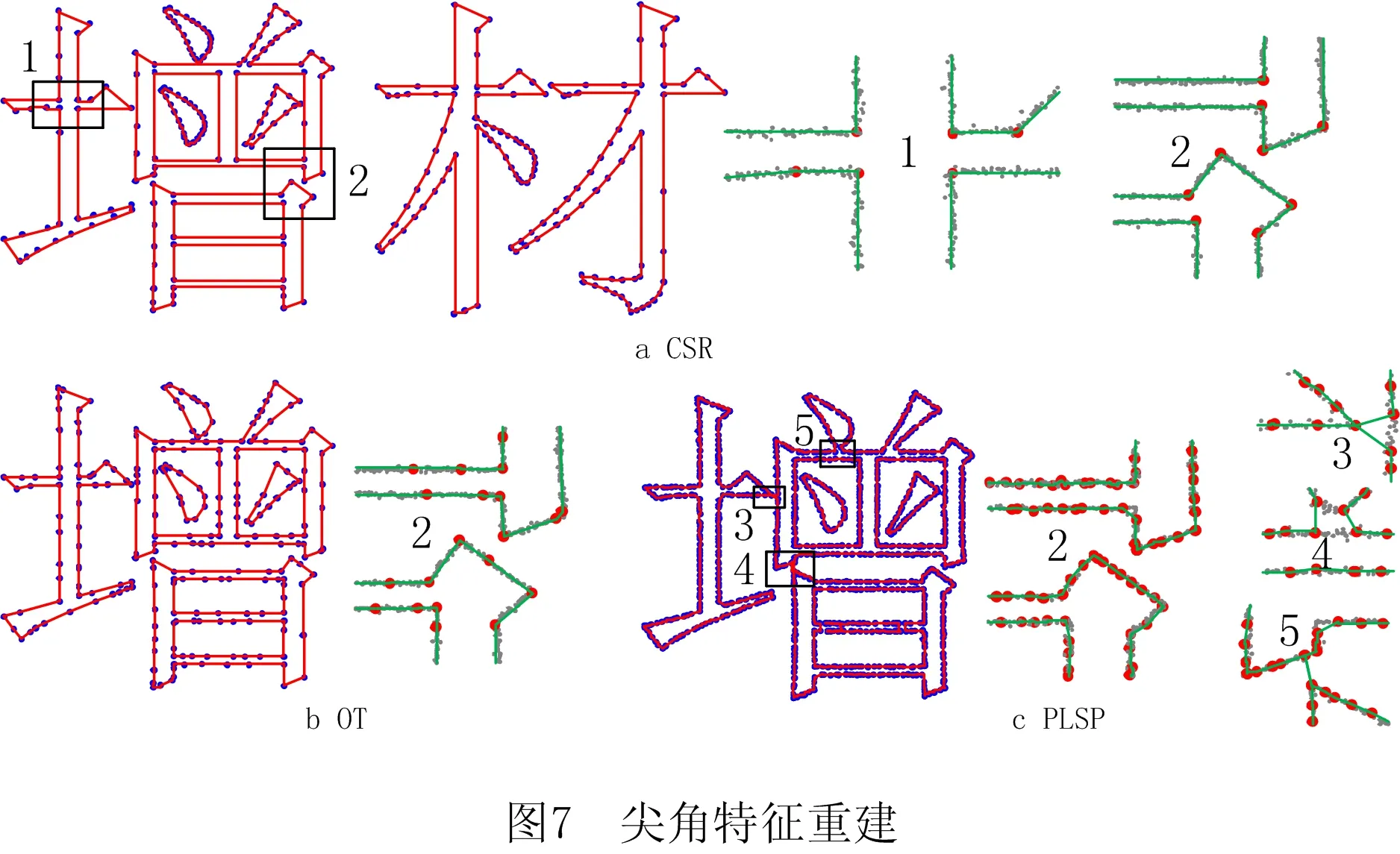
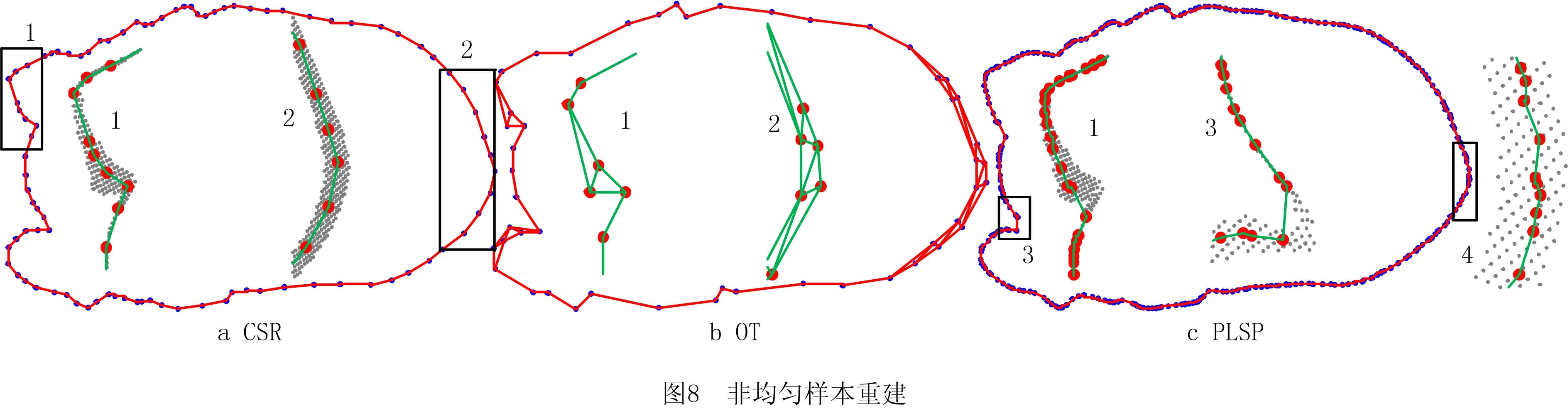
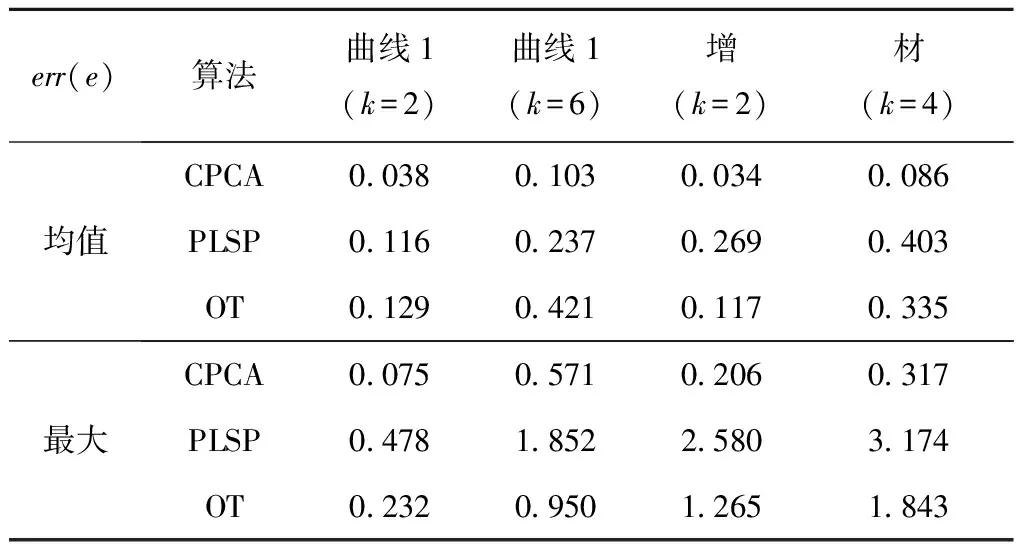
表1 多义线重建几何误差的比较 %

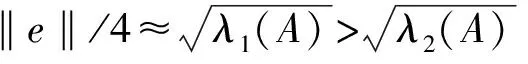
图8和图9的算例验证了CPCA处理非均匀和稀疏样本的能力，样本点采用图1中的直接投影法得到，分别包含2 062和791个点。3种算法在图8和图9中的对比结果表明，CPCA和PLSP均可处理投影点云带宽度不均匀的情形，而OT在宽度较大的区域生成分叉边。PLSP采用直接投影法生成样本，因此可能导致相邻曲线无法分辨，在与分层平面接近于平行的区域采样时，需要减小图1中的参数d，或调整用于识别相邻曲线的距离参数，这样的用户干预导致成百上千层曲线的自动重建较困难，而本文采用的虚拟边采样方法避免了这一问题。如图9a的样本分布所示，当样本存在局部缺失时，CPCA仍可得到图9b中正确的拓扑结构，但已无法重建曲线的细节特征。对于这种特殊情形，可对多义线进行拟合得到光滑的样条曲线[12]。

为验证CPCA对实测点云的分层效果，使用形创HandySCAN(TM)扫描仪获取图10a中的4组点云，分别为720°螺旋叶轮、传动螺杆、狗雕塑、鞋模。由于采用非接触式测量，点云在自相遮挡区域存在部分缺失。点云4的分层方向垂直于图像平面，前3个点云沿图像列方向分层，图10b～图10e所示为分层结果，其中的层片每间隔数层显示1层。为衡量CPCA的增量分层特性，将边按其创建的先后顺序编号，执行增长、删除和拓扑算子时，若既有移除边也有新增边，则后者编号继承自前者。若第k层的某边在k-1层也存在，则称为继承边，单层上继承边的占比称作继承比，边在单层上的平均学习次数简称为平均学习，表2所示为继承比和平均学习次数在所有层上的均值。另外，将连接相邻层相同编号边的曲线称为层间映射线。

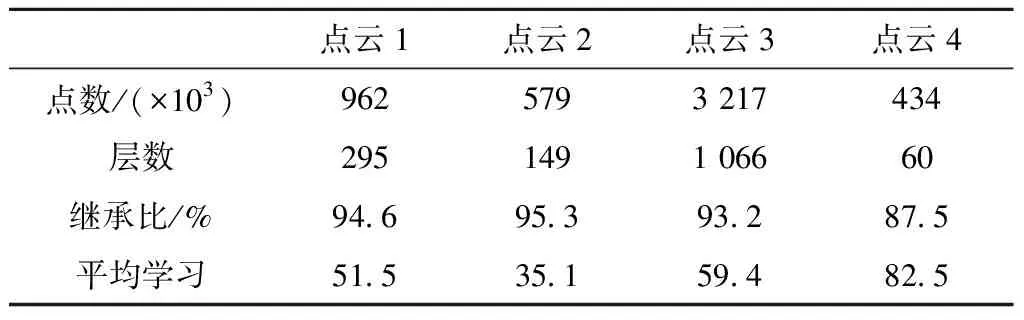
表2 点云分层基准测试

叶轮模型两端是平行于分层方向的中轴，层厚为1 mm时，端部约30 mm范围内(图11a曲线上的箭头标识)CPCA快速收敛，继承比大于98%；螺旋上升的叶片部分的继承比在90%～98%之间波动，平均学习次数与继承比呈反相关。图12所示为继承边的运动轨迹，其中多数继承关系延续数十层不间断。图10c所示为螺杆层片的侧视图，螺杆的外轮廓呈圆柱形，但上下两端存在齿槽导致的拓扑结构变化，对应图11d平均学习曲线上标识的尖峰，因此拓扑突变比同胚变形更耗时。另外，螺杆点云的平均学习曲线呈U型下降后上升，与圆柱轮廓截面的变化趋势一致，即单层收敛时间随同胚变形量增长。由图10e可见，点云4鞋底有复杂的花纹，其在表2中的平均学习次数显著高于其他3组数据。以上对不同层及不同点云的比较表明，本文算法可有效利用层间形状的相似性来提高分层效率。

为进一步验证CPCA增量分层对效率的贡献，对不同分层方式的运行时长进行比较，得到表3所列数据。表中的分层时间包括了图1中样本生成方法的耗时和后续的曲线重建耗时。为获得有意义的比较结果，两个阶段都需要合理设置影响耗时的参数，样本生成时参数d(如图1)统一取1.3 mm。在曲线重建时，PLSP，OT，CPCA具有不同的参数。其中，PLSP构建初始轮廓时按建议值[7]取k近邻为40，移动顶点时，当其振幅小于平均边长的5%后停止迭代；OT迭代删除边直到数量与CPCA输出相同，将其加速选项全部打开，而且构造初始Delaunay剖分时仅使用15%样本；CPCA除学习率外无其他参数，取默认值5%。

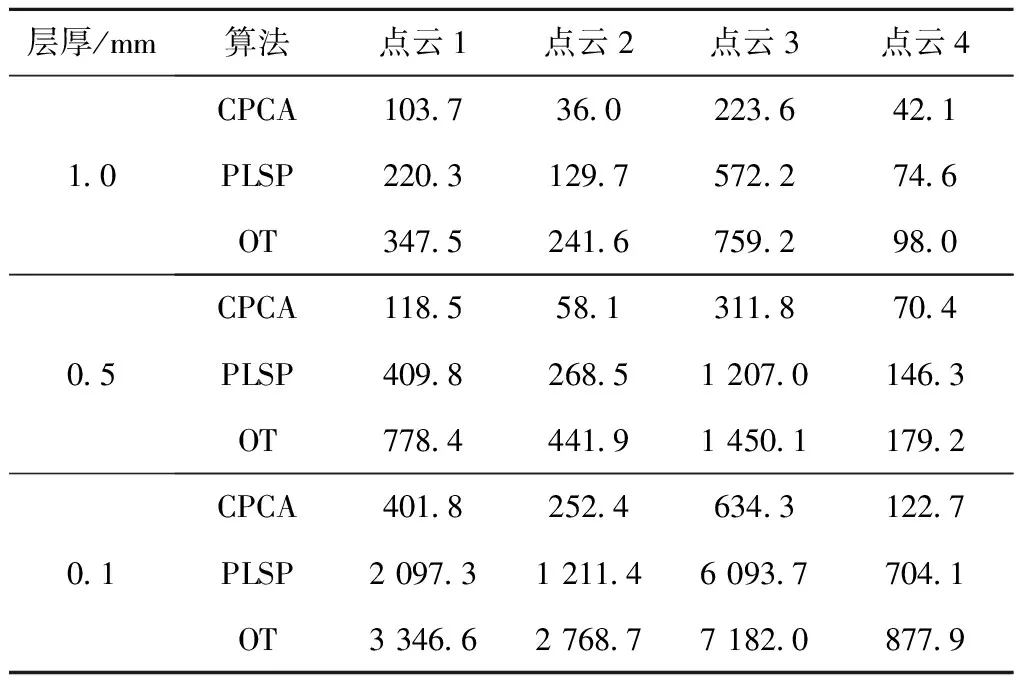
表3 分层时间比较 s

由表3可知，当点云1的层厚由1 mm降低到0.5 mm时，CPCA整体耗时仅略为增长，即单层耗时减半，而PLSP和OT的单层耗时与层厚无关。比较表明，CPCA增量分层较每层从头构建多义线的方法(PLSP和OT)缩短了计算时间，而且效率优势随层厚的降低更加显著，这是由于CPCA的边平均学习次数与层厚相关。如图11c和图11f所示，层厚为0.1 mm时多数层片在1～2次检查后便收敛，边平均学习10～20次。现有的选择性光固化、数字光投影、选择性激光熔融等增材制造方法已将层厚降至数十微米，因此CPCA在实际应用中具有极低的边平均学习次数，可以利用层间相似性显著加速分层过程。虽然较非增量式的点云分层方式大幅提高了效率，但是CPCA仍不及网格分层[21]，若不考虑点云转换为STL模型的复杂性及手动修复网格的耗时,表3算例中等价的网格模型分层耗时均小于1 min。

表4统计了不同分层方式下拓扑错误的数量，包括非封闭多义线、相交边、分叉线(某顶点连接到多于两条边的情形)。除这3类拓扑错误外，还将点云重构为STL文件后使用Minetto[21]的开源程序进行分层处理，网格分层与点云分层所得多义线数量的差值也计入表4中的拓扑错误数量。在CPCA输出中未发现相交边和分叉线，表4列出了其步骤8修复前/修复后的错误数。点云1～点云3的分层错误均被修复，点云4鞋底花纹区遗留了部分开线，这些开线归因于统计学习的非确定性，花纹部位点云密度不足会加剧非确定性。在所有测试案例中，点云4的样本数量最少，实验特意选定了一个使截面轮廓拓扑变化最剧烈的分层方向，即使采用点云重建网格+网格分层的处理方式，花纹部分也需用耗时的网格手动修复才能避免拓扑错误。由表4可知，本文的增量分层方法通过继承相邻层的学习结果降低了拓扑错误发生的概率(修复前)，而且步骤8进一步利用层间的相似性修复了可能的拓扑错误。对于层间相似性小的低密度点云，可多次迭代执行步骤8，从而用降低算法效率换取拓扑正确性。另外，实际应用中可通过缝合开线的最近邻端点对来闭合多义线，但该操作在处理复杂拓扑结构时可能需要手动修复。图13所示为点云4分层数据(0.1 mm层厚)经过修复后用SLA打印得到的树脂件。

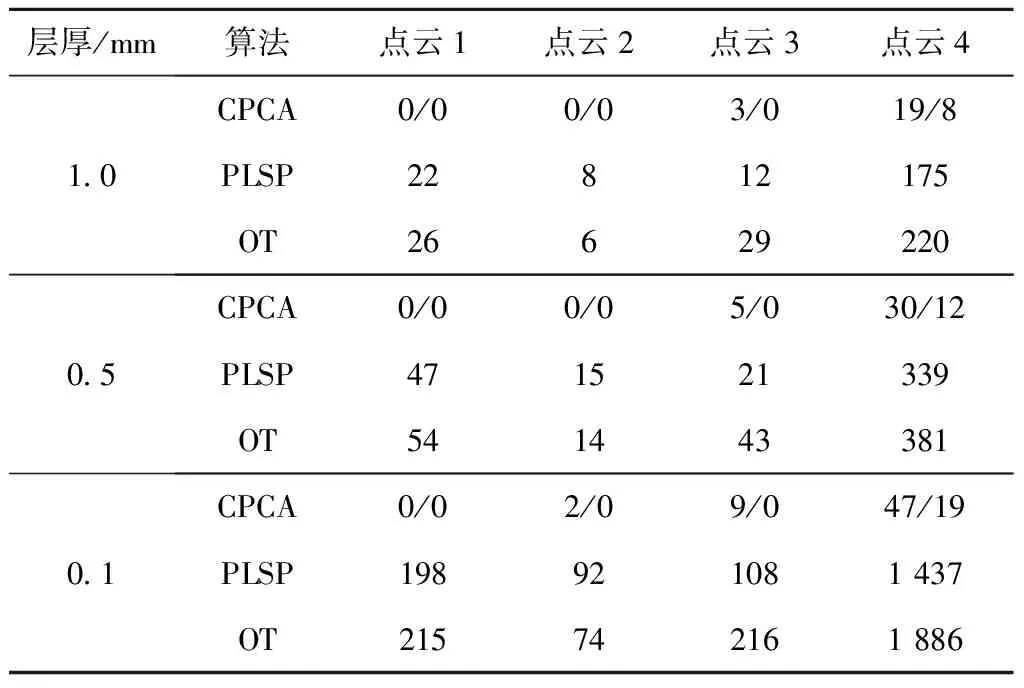
表4 拓扑错误的数量比较

CPCA仅开放学习率这一参数，所有实验取默认值5%。较大的学习率可加快网络收敛，但会增加需要步骤8修复的拓扑错误。由于点云3和点云4的截面轮廓变化较大，PLSP和OT很难通过固定参数得到拓扑错误较少的结果。在表4中，实验将两组点云沿Z方向手动分割为数个区间，并单独调整每个区间的参数，发现OT中控制输出边数量的参数和PLSP中分辨多条曲线的参数对拓扑错误起主导作用。虽然引入了手动干预，但是OT和PLSP方法的拓扑错误数仍高于CPCA。在重建成百上千层曲线时，参数优选成为不可忽视的问题，现有文献[3-19]对此关注较少，而增量分层利用层间相似性为其提供了可能的解决思路。

4 结束语

本文提出一种非监督学习网络CPCA，由点云增量式地构造增材制造用的各层曲线。CPCA设计了一套移动、增长、删除、拓扑变换学习机制，在对输入点云假定最少先验知识的条件下，可连续追踪变化的曲线，并利用相邻层片的拓扑和几何相似性避免从头构造每层曲线，该相似性用于从噪声、数据缺失等异常输入中恢复尖角、凹凸性等显著特征，以及从学习历史中继承正确的拓扑关系。实验将CPCA与非增量式PLSP和OT算法相比，结果表明CPCA可提高成百上千层密集堆叠层片的构造效率，且在无用户干预下重建拓扑结构较复杂的截面轮廓。然而，作为统计学习网络，CPCA的输出是非确定的，后续研究将通过增加迭代次数、批量学习等策略来完全消除复杂模型的拓扑错误。