叶片抛光表面粗糙度与残余应力优化分析

刘 德，史耀耀，蔺小军，鲜 超，谷志阳,2

(1.西北工业大学 机械电子工程学院，陕西 西安 710072;2.温州职业技术学院 控制科学与工程学院，浙江 温州 325035)

0 引言

TC17为一种典型的α+β型钛合金，因比强度高、耐高温性佳、抗腐蚀性好等特性被应用于航空发动机叶片[1-2]。为充分发挥钛合金良好的机械性能，提高叶片的工作寿命，要求叶片表面具有良好的表面完整性，作为机加工的最后一道工序，抛光对表面完整性起决定作用。为提高加工后工件表面的完整性，国内外学者针对复杂型面的磨抛加工展开了一系列研究。

针对钛合金整体叶盘结构复杂、叶片薄、开敞性差等特点，实验选用自行设计的五轴联动数控抛光机床，采用百叶轮对航空发动机整体叶盘、叶片等复杂型面构件进行抛光[3-4]。百叶轮体积小、结构简单，具有良好的可达性，可深入开放性差的复杂型面进行抛光；而且百叶轮高速旋转，其抛光片受离心力作用充分伸展，能够获得良好的弹性，从而对复杂型面进行随形切触，并使抛光力更加稳定[5]，抛光效果更好。

Grzesik等[6]研究用立方氮化硼(Cubic Boron Nitride，CBN)硬质砂轮精密磨削加工的能耗，并通过平衡比能与犁能优化了硬加工操作，降低了能耗；Kuo等[7]开发了一种Ace-Tone气相抛光系统，对熔融沉积模型制备的丙烯腈—丁二烯—苯乙烯零件进行抛光，通过复杂的几何结构降低了表面粗糙度；Xiao等[8]采用点到点法优化抛光路径，形成精细均匀的纵向微痕，提高了精度一致性；Liu等[9]研究了Ti-6Al-4V的磨削加工，提高了加工效率和表面质量；张军锋等[10]研究了砂带抛光表面粗糙度，优化了工艺参数，降低了加工表面粗糙度；Zhao等[11-12]对抛光进行一系列研究，提高了工件的表面完整性，以及抛光系统的可靠性和效率；Yao等[13-14]通过优化磨抛工艺参数研究了一系列表面完整性和疲劳行为，提高了工件的疲劳寿命；张军锋等[15]采用灰色关联模型对砂带抛光叶片表面的粗糙度和材料去除效率进行分析，在改善抛光表面粗糙度的同时提升了抛光过程中的材料去除效率；计时鸣等[16]分析了气囊抛光的工作原理、特点和发展现状，并对其关键技术进行了比较分析，研究结果表明，气囊抛光可有效对自由曲面进行高效精密抛光；Silva等[17]分析了磨削过程中润滑剂的性能，采用流体分析方法优化润滑剂用量，对磨削表面完整性的改善起到积极的作用；刘薇娜等[18]通过正交试验探索了抛光压力、磨料浓度、磨粒粒径和加工时间等工艺参数对被抛光微孔表面粗糙度的影响规律，结果表明，喷油嘴微孔磨粒流单向循环抛光加工有利于改善喷孔结构，各加工参数、抛光压力和磨料浓度对抛光流道的表面粗糙度有显著影响。

根据以上文献可知，目前对百叶轮抛光的研究主要是为降低表面粗糙度而进行的抛光机构改进和工艺参数优化，对抛光后表面残余应力状况的分析较少。大量研究表明，表面粗糙度对工件的耐磨性、疲劳寿命、接触刚度和冲击强度等有重要影响，表面残余应力对工件的疲劳强度、尺寸精度等有重要影响[19-22]。因此，提高表面完整性不能单纯地降低表面粗糙度。

百叶轮的抛光力虽然相对较小，但是仍会产生大量抛光热，抛光导致的高温对残余应力的影响不容忽视；钛合金导热系数低(仅为铝的1/4，钢的1/5)，摩擦系数大，使磨抛过程中产生的热量无法迅速传导出去，容易造成残余拉应力，降低工件的机械性能和寿命。因此本文以改善抛光后钛合金叶片的表面粗糙度与残余应力为目的优化工艺参数，对提高钛合金叶片工作寿命有积极的意义。

1 实验条件和方案

1.1 实验平台

实验选用TC17钛合金叶片，化学成份如表1所示；选用布基、SiC磨料的百叶轮为抛光磨具；采用五轴联动的数控机床作为抛光设备，如图1所示；百叶轮安装在磨削主轴上，磨削主轴可沿坐标轴X，Z完成直线运动，沿A完成偏摆运动；磨削主轴径向均布3个气缸，通过控制气缸压强调整磨削主轴径向位姿；每个气缸对面布置一个位移传感器，可对磨削主轴位移进行监测，并实现气缸位移的反馈调节，提高加工精度；钛合金叶片固定在机床上，可沿坐标轴Y方向做直线运动，沿U方向做旋转运动，各机构相互协同来调整磨头抛光位姿，完成叶片的抛光加工。

表1 TC17钛合金的化学成分 %

1.2 测量条件

在实验过程中，根据各组实验的工艺参数依次对叶片进行抛光实验，然后测量抛光区域的粗糙度和残余应力，并观测微观形貌，从而分析各参数条件下叶片的抛光效果。由于百叶轮对叶片的叶盆和叶背进行抛光时的材料去除量很小(约20 μm)，实验不考虑抛光对型面精度的影响。

叶片表面粗糙度采用Mahr粗糙度轮廓综合测量仪测量，该测量仪采用内置激光测量系统，单次测量可同时测量轮廓和粗糙度。集成于内部的专用激光干涉仪可提供大范围、高分辨率的高精度测量；驱动臂使用桥式结构设计，可保证测量过程中的结构刚性；测量力从0.5 mN～50 mN(软件选择电子控制调整)，可根据不同测量臂选择合适的测量力，以提高测量精度。在粗糙度的测量过程中，每次在待测面随机选取5个点取平均值为最终测量结果。

采用X射线残余应力分析仪测量百叶轮抛光后钛合金叶片的残余应力。X射线衍射法是一种无损测量技术，可用于测量不透明材料的表面残余应力。试件中存在的残余应力使晶格间距离发生变化，用波长为λ的X射线以不同的入射角照射实验件，当发生拉布拉格衍射时，产生的衍射峰将随之移动，通过分析不同X射线入射角照射钛合金时的衍射角，结合残余应力计算公式，可得钛合金叶片表面的残余应力。每次测量在待测面随机选取不同方向和不同位置的5个点，测其残余应力，取平均值为该面残余应力。

1.3 磨具与抛光面的初步分析

在显微镜放大100倍下，观察抛光后百叶轮的表面微观形貌特征，如图2所示。可见，部分磨粒磨损，靠近百叶轮边缘的磨粒磨损严重，而且布基上也有烧焦的痕迹，原因是在抛光过程中产生了大量的热量，高温引起残余压应力减小。因此，抛光过程对残余应力的影响不容忽视。

铣削和抛光后叶片的表面微观形貌如图3所示。在100倍显微镜下，铣削表面形貌如图3a所示。点接触铣削后，钛合金叶片的表面粗糙度为1.125 μm，表面残留高度明显，微裂纹较多，需要进一步抛光以降低表面粗糙度。抛光表面形貌如图3b所示，采用百叶轮抛光后，钛合金叶片表面粗糙度为0.376 μm，粗糙度明显降低。与抛光前相比，有效去除了铣削后叶片表面的残留高度，改善了表面纹理，明显减少了表面微裂纹，然而抛光表面仍有一些刀痕和凹槽，需要进一步优化抛光工艺参数来提高抛光表面质量。

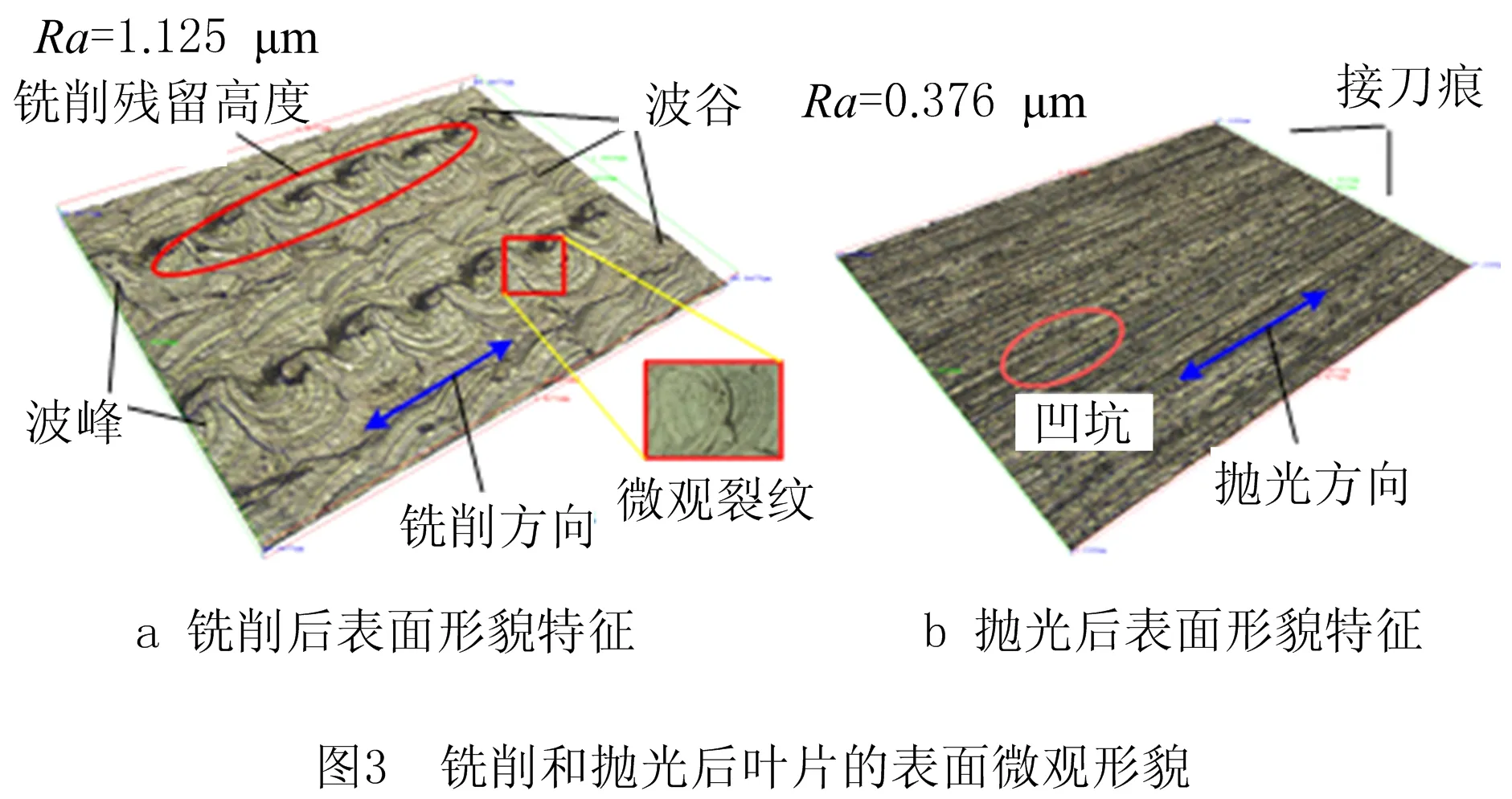
以上分析表明，抛光降低表面粗糙度的同时，加工过程中产生的热量也降低了表面残余压应力，因此需要对抛光参数进行优化分析使其更加合理，以在保证表面粗糙度的同时尽可能保留较大的残余压应力。

1.4 单因素实验

利用实验平台在叶背进行抛光实验，并保证叶片在抛光区域走刀5次，研究单因素对粗糙度Ra，残余应力σ和表面微观形貌的影响，如图4所示。

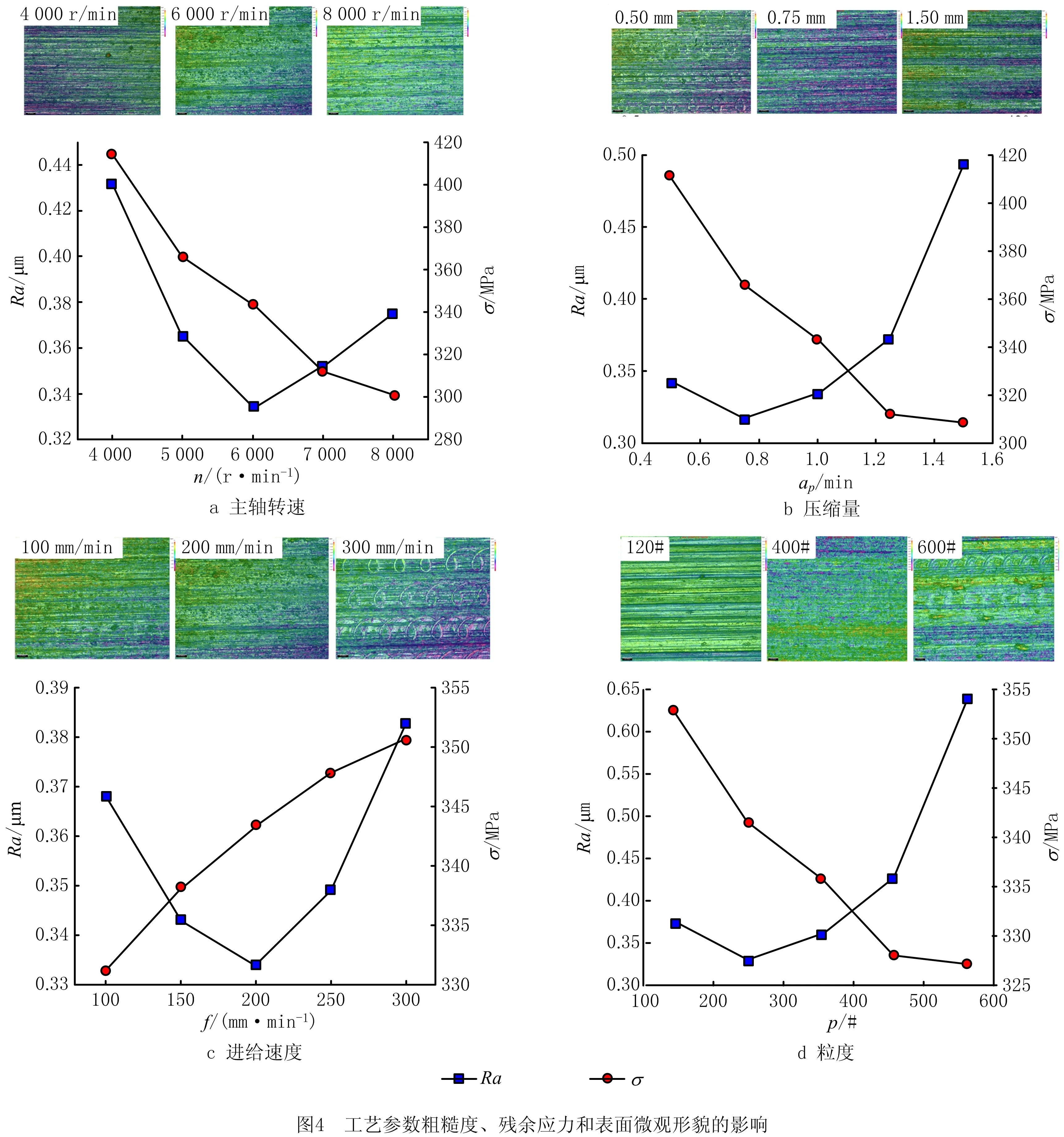
如图4a所示，粗糙度随主轴转速的增加先减小后增大。根据抛光叶片的表面形貌，主轴转速为4 000 r/min时，叶片表面纹理明显，主要原因是主轴转速较低，砂布片展开量较小，未能充分发挥百叶轮的高弹性，每个磨粒完成一次切削需要较长时间，导致较大的切削深度。随着主轴转速的增加，百叶轮完成一圈旋转的时间缩短，减小了每一圈的单次切削厚度。当主轴转速达到6 000 r/min时，百叶轮有良好的柔性及合理的切削深度，因此抛光后的表面粗糙度降低。当主轴转速为8 000 r/min时，百叶轮因其圆柱度和同轴度误差而产生高频振动，造成抛光过程不平稳，导致叶片表面粗糙度增大，残余应力单调下降。其原因是随着主轴转速的增加，抛光时间和抛光热增加，导致表面残余压应力降低。

如图4b所示，粗糙度随压缩量的增加先减小后增大，结合叶片表面微观形貌，分析该现象的主要原因。压缩量较小时抛光力小，百叶轮对叶片表面的主要作用是滑动和犁削，根据压缩量为0.5 mm的表面微观形貌可知，压缩量较小时材料去除量不足，使得叶片表面铣削残留高度不能被完全去除。当压缩量增加为0.75 mm时，百叶轮进入正常抛光状态，降低了抛光表面的粗糙度。随着压缩量的继续增加，抛光力进一步增大，各磨粒的单次切削厚度增大，导致抛光表面粗糙度增大。例如压缩量为1.5 mm的表面微观形貌，抛光表面的纹理较明显，残余压应力单调下降。其原因是增加压缩量引起抛光力增加，产生更多抛光热，导致抛光后的表面残余压应力降低。

如图4c所示，粗糙度随进给速度的增加先减小后增大，主要原因是，当进给量比较小时，不能将抛光热及时传导出去，导致抛光表面热变形增大，影响了抛光精度，例如进给速度为100 mm/min时的抛光表面微观形貌，随进给速度的增加，抛光表面的散热效果明显改善，抛光表面粗糙度降低；当进给速度为200 mm/min时，单位面积的抛光时间过短，无法完全去除残余高度，例如进给速度为300 mm/min时的抛光表面微观形貌，铣削残留高度未完全去除，导致粗糙度增大，残余压应力单调增加。其原因是随着进给速度的增加，抛光单位面积产生的热量减少，使残余压应力增大。

如图4d所示，粗糙度随百叶轮粒度的增加先减小后增大。其原因可能是随着粒度的增加，百叶轮砂布片表面单位面积的磨粒数增多，磨粒体积减小，材料去除能力降低，各磨粒的单次材料切削厚度与宽度减小，有利于降低抛光表面纹理。随着粒度的增大，磨粒体积进一步减小，单颗磨粒的去除量过小，抛光效率降低，导致叶片表面铣削残余高度不能完全去除。残余压应力随着粒度的增加而单调变大，其原因可能是随着粒度的增大，去除效率降低，单位时间内百叶轮的材料去除厚度减小，且抛光热减少，使抛光后的叶片表面残余压应力增大。

分析单因素对粗糙度和残余应力的影响规律可知，叶片表面的最小粗糙度与最大残余压应力对应的最佳工艺参数不同，想要提高抛光后叶片的表面完整性，不能将粗糙度和残余应力分离，需要综合分析抛光后叶片表面的粗糙度和残余应力，在保证粗糙度的前提下，尽可能保留较大的残余压应力。

2 实验设计与建模分析

2.1 实验设计

影响百叶轮抛光的工艺参数主要包括主轴转速n、压缩量ap、进给速度f和粒度p[21]。根据以上单因素实验所得的曲线，选取各参数范围，使其体现参数曲线的变化趋势：主轴转速4 000 r/min～8 000 r/min，压缩量0.5 mm～1.5 mm，进给速度100 mm/min～300 mm/min，粒度120#～400#。选择布基、SiC磨料的百叶轮为抛光工具，刀具直径×长度=15 mm×12 mm。抛光参数水平分布如表2所示。

表2 抛光参数水平分布

为了降低实验次数，采用Taguchi法的正交设计，σ为抛光后的表面残余压应力(单位：MPa)，Ra为表面粗糙度(单位：μm)，具体工艺参数和实验结果如表3所示。

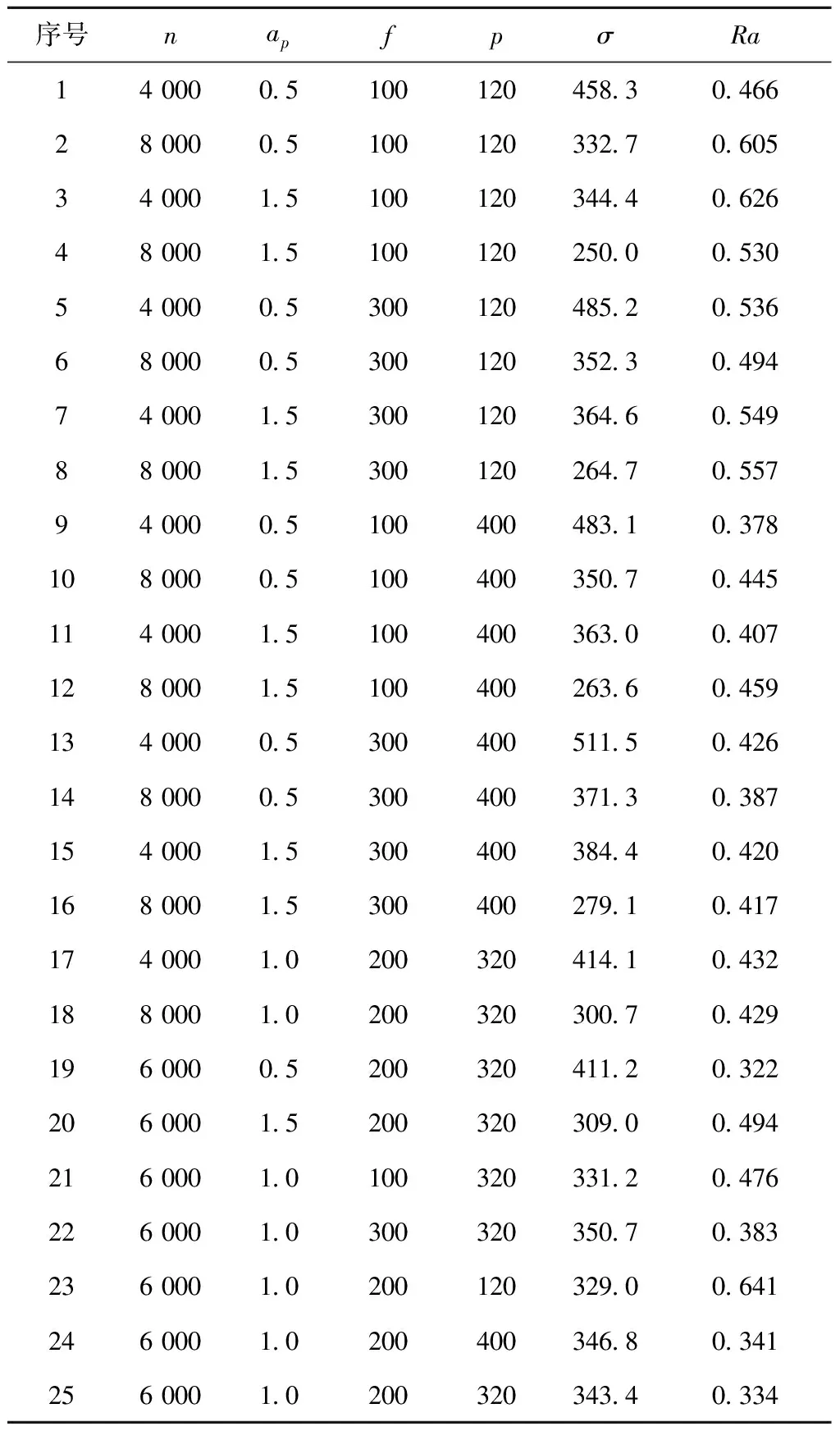
表3 正交试验结果

2.2 预测模型的建立

根据单因素实验，分析工艺参数对抛光表面粗糙度与残余应力的影响规律，采用二阶回归方程对粗糙度预测模型进行建模，采用经验模型对表面残余应力预测模型进行建模：

(1)

(2)

式中：a，b为预测模型系数；x为不同的工艺参数。将表3的实验数据代入式(1)和式(2)，可得各项回归系数，则粗糙度与残余应力的预测模型如下：

Ra=0.621-4.12×10-6n+0.228ap

-1.059×10-6-1.84×10-3p+2.32×

2.39×10-6p2-1.025×10-5nap-

7.44×10-8nf+1.37×10-8np-3.5×10-5

apf-3.44×10-5app+9.96×10-8fp；

(3)

(4)

为检验预测模型的显著性，采用F检验法对粗糙度与残余应力预测模型进行显著性检验[21]。如果F>F0.01(p,n-p-1)，则表示目标函数与参数之间有十分明显的线性关系，回归方程可信。采用Design-Expert分析粗糙度与残余应力预测模型，模型显著性检验如表4所示。其中：df为自由度，SS为平方和，MS为均方和，F为F值统计量。

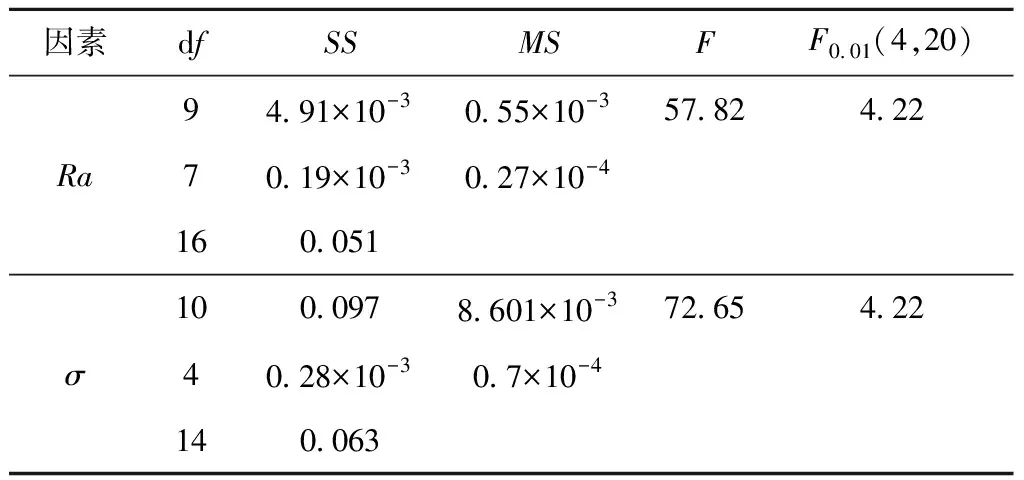
表4 模型显著性检验

由表4可知，粗糙度与残余应力的F值分别为57.82，72.65，均大于F0.01(4,20)，因此预测模型显著性良好，可用于分析粗糙度与残余应力。

2.3 敏感性分析

相对敏感分析可以综合反映各目标参数对工艺参数的敏感程度[23]，计算公式为

(5)

式中：S′(xk)为目标参数的相对灵敏度；f(x)为目标函数，x=(x1,x2,…,xn)；xk为目标参数。

将残余应力预测模型代入式(5)，计算可得残余应力对工艺参数的相对灵敏度Sσ′(n)=0.461 9，Sσ′(ap)=0.260 1，Sσ′(f)=0.152，Sσ′(p)=0.043 8，显然残余应力对主轴转速的变化最敏感，压缩量和进给速度次之，对粒度的变化最不敏感。

2.4 稳定域划分

为划分粗糙度与残余应力的工艺参数稳定域，进行灵敏度分析，计算公式为

(6)

式中S(xk)为一阶灵敏度。

将粗糙度预测模型带入式(6)，可得粗糙度对工艺参数的灵敏度模型：

(7)

根据粗糙度对工艺参数的敏感性分析，结合工艺参数对粗糙度的影响规律，对粗糙度进行工艺参数的敏感性分析和稳定域划分(划分规则见文献[23])，如图5所示。首次稳定域划分标记为Stable1，首次非稳定域划分为Unstable1；第2次稳定域划分为Stable2，第2次非稳定域划分为Unstable2。

将表面残余应力预测模型带入式(6)，可得粗糙度对工艺参数的灵敏度模型，如式(8)所示。

(8)

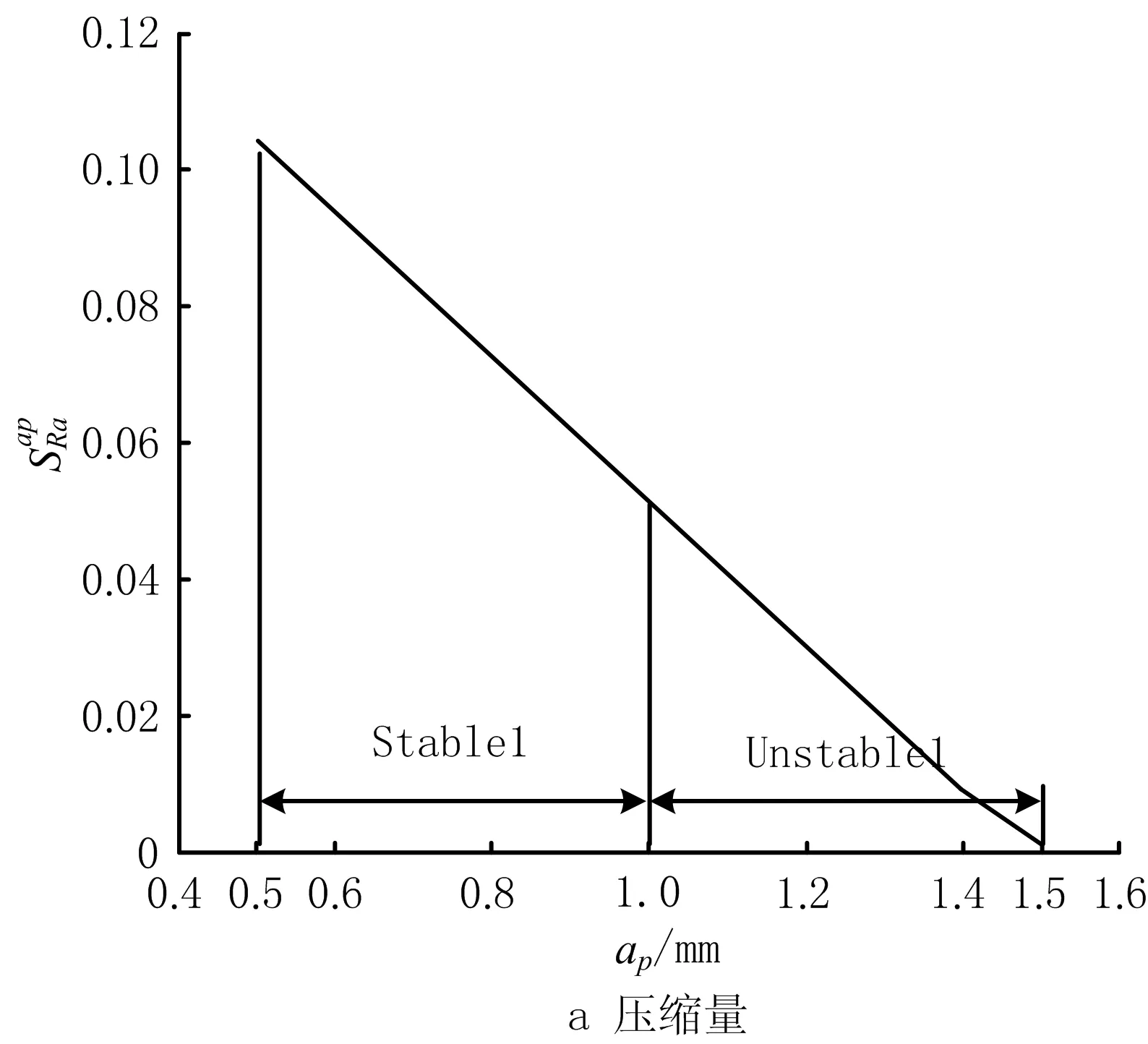
根据残余应力对工艺参数的敏感性分析，结合工艺参数对残余应力的影响规律，对残余应力进行工艺参数的敏感性分析与稳定域划分，如图6所示。首次稳定域划分为Stable1，首次非稳定域划分为Unstable1。第二次稳定域划分为Stable2，第二次非稳定域划分为Unstable2。

根据稳定域的划分结果，为工艺参数优选参数区间。通过粗糙度与残余应力的灵敏性分析和稳定域划分结果，可得粗糙度与残余应力的优选区间，取两者相交区间为最终优选区间，如表5所示，主轴转速、压缩量、进给速度和粒度的最终优选区间分别为5 000 r/min～6 000 r/min，0.75 mm～1.0 mm，150 mm/min～300 mm/min，260#～400#。

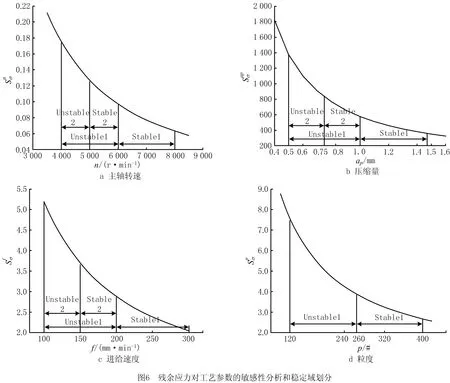
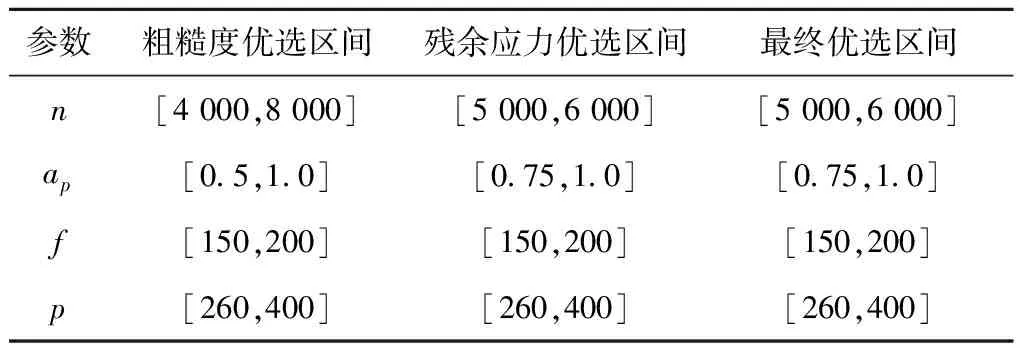
表5 工艺参数优选区间

3 灰色关联分析

3.1 数据转换和等权关联系数的计算

等权关联系数的求解过程如式(9)～式(12)所示。表面残余压应力可以提升工件的抗疲劳强度，有利于提高工件的机械强度，残余压应力数据变换如式(9)所示；表面粗糙度对工件耐磨性、疲劳寿命、接触刚度和冲击强度等有重要影响，较小的表面粗糙度有利于提高工件的机械性能和工作寿命，粗糙度数据变换如式(10)所示；分别计算每个比较序列和参考序列对应的关联系数，如式(11)所示；分别计算残余应力、粗糙度和参考序列对应元素的均值，以反映评价对象和参考序列之间的关联关系；等权关联系数计算如式(12)所示。

(9)

(10)

η=

(11)

(12)

式中：yi(k)为变换后的数列；xi(k)为原始数列；x0(k)为初始值；η为灰色关联系数；ρ为分辨系数；y0(k)为参考数列的最优值，由表7分析可知残余应力变换后数列的最优值y0(σ)=0.881，粗糙度变换后数列的最优值y0(Ra)=0.851；0<ρ<1，通过查询手册此处取0.5。

根据式(9)和式(10)对残余应力和粗糙度进行数据转换，由式(11)可得灰色关联系数，式(12)可得等权关联系数，如表7所示。

3.2 响应权重和灰色关联度计算

通过主成分分析(Principal Components Analysis, PCA)对数据进行降维可定量得出各参数对应的影响程度。采用PCA计算残余应力和粗糙度的灰色关联影响权重(即贡献率)，建立多种质量特征的原始序列矩阵X，

(13)

式中：m为实验次数，m=25；n为目标响应数，n=2。

相关系数数组的计算方法如下：

(14)

|λkI-R|=0；

(15)

(16)

式中：Cov(xi(j),xi(l))为xi(j)和xi(l)的协方差，j,l=1,2,…，n；Dx为方差；I为单位矩阵；αk为残余应力与粗糙度的影响权重。用式(15)可求得特征值λk。

根据式(13)建立原始序列矩阵，然后用式(14)算出系数矩阵R，用式(15)求出特征值，最后用式(16)求得残余应力和粗糙度的影响权重，如表6所示。

表6 主成分分析结果

由表6分析可知，表面粗糙度Ra所对应特征值为1.210 1，贡献率为60.5%，为第一主成分；表面残余应力所对应的特征值为0.789 9，贡献率为39.5%，为第二主成分。灰色关联度为灰色关联系数的加权和，如式(17)所示:

(17)

式中，βk为主成分贡献率。

根据表6可知粗糙度和残余应力的贡献率，β1=0.605，β2=0.395。用式(14)计算灰色关联度，如表7所示。

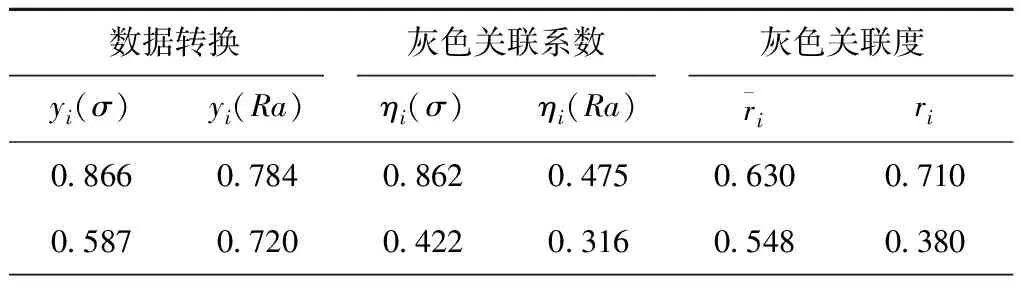
表7 等权关联系数

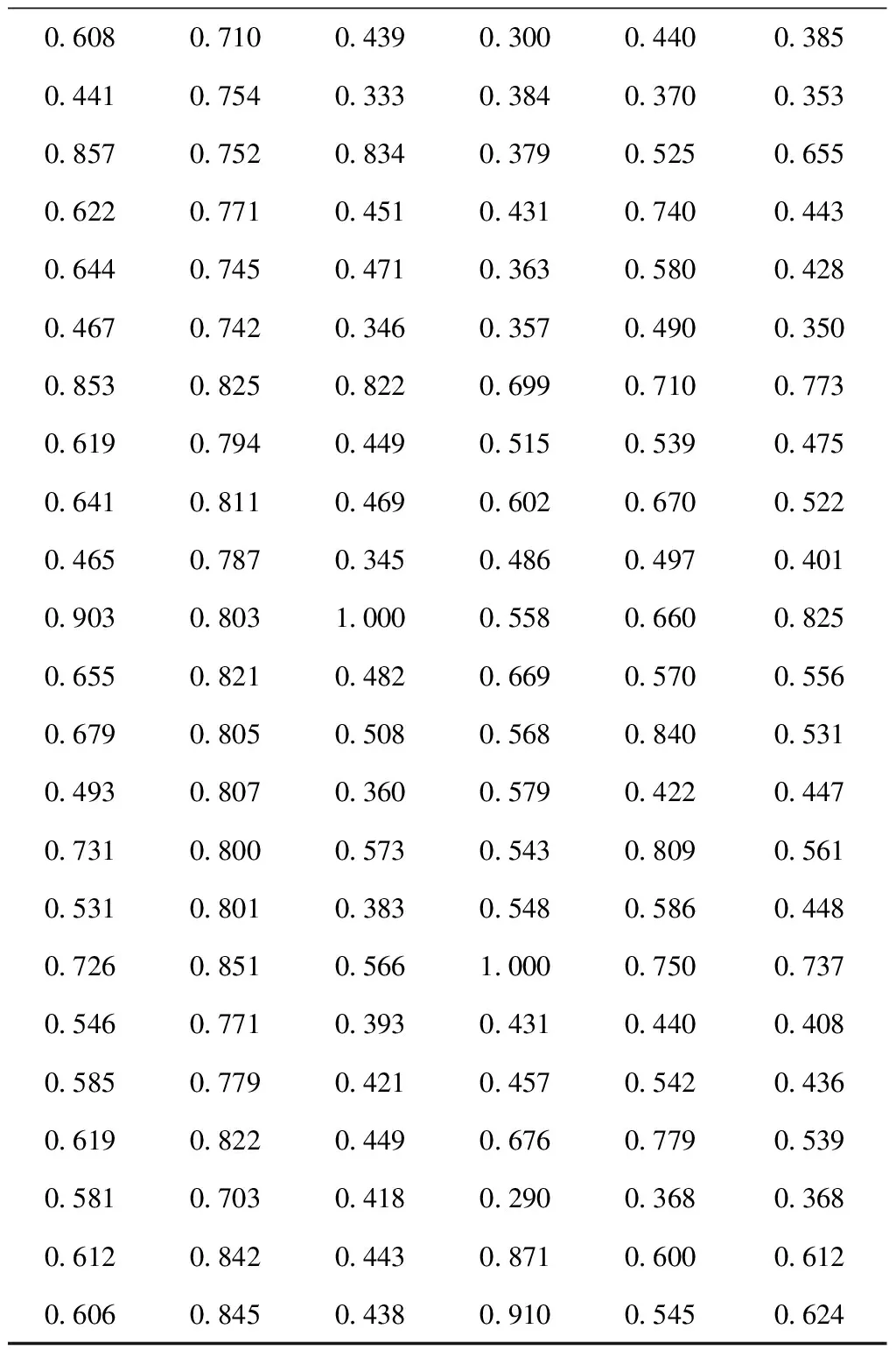
续表7

3.3 优化模型的建立

为对抛光工艺参数进行优化，需构建各工艺参数与灰色关联度之间的函数关系，因为各参数与目标函数之间为非线性关系，所以采用二阶回归方程表示为

(18)

式中：r′为灰色关联度预测值；ε为实验误差；a为二次回归方程系数；xi，xj为抛光工艺参数。

利用Design-Expert对实验数据进行二次回归分析，计算预测模型的方程系数，得到灰色关联度与各工艺参数之间的预测模型为

r′=0.681 5-1.664 7×10-4n-0.041 3ap

-1.290 1×10-3f+5.102 6×10-3p-4.05

×10-5nap+3×10-8nf-1.811×

10-7np+2.125×10-4apf+3.118×

10-4app-3.725×10-7fp+1.787×

7.445 6×10-6p2。

(19)

灰色关联度的实验值与预测值对比如图7所示。由图7a可知，灰色关联度的真实值与预测值的差值较小，说明预测值误差较小；图7b所示为灰色关联度预测模型的残差图，可见数据沿直线分布，实验点与模型拟合程度良好，呈现为线性关系，表明预测模型与真实值吻合度高，因此该模型可用于预测分析灰色关联度。

3.4 影响规律分析

利用主效应法分析各抛光工艺参数对残余应力、表面粗糙度的灰色关联系数和灰色关联度的影响，如图8所示。

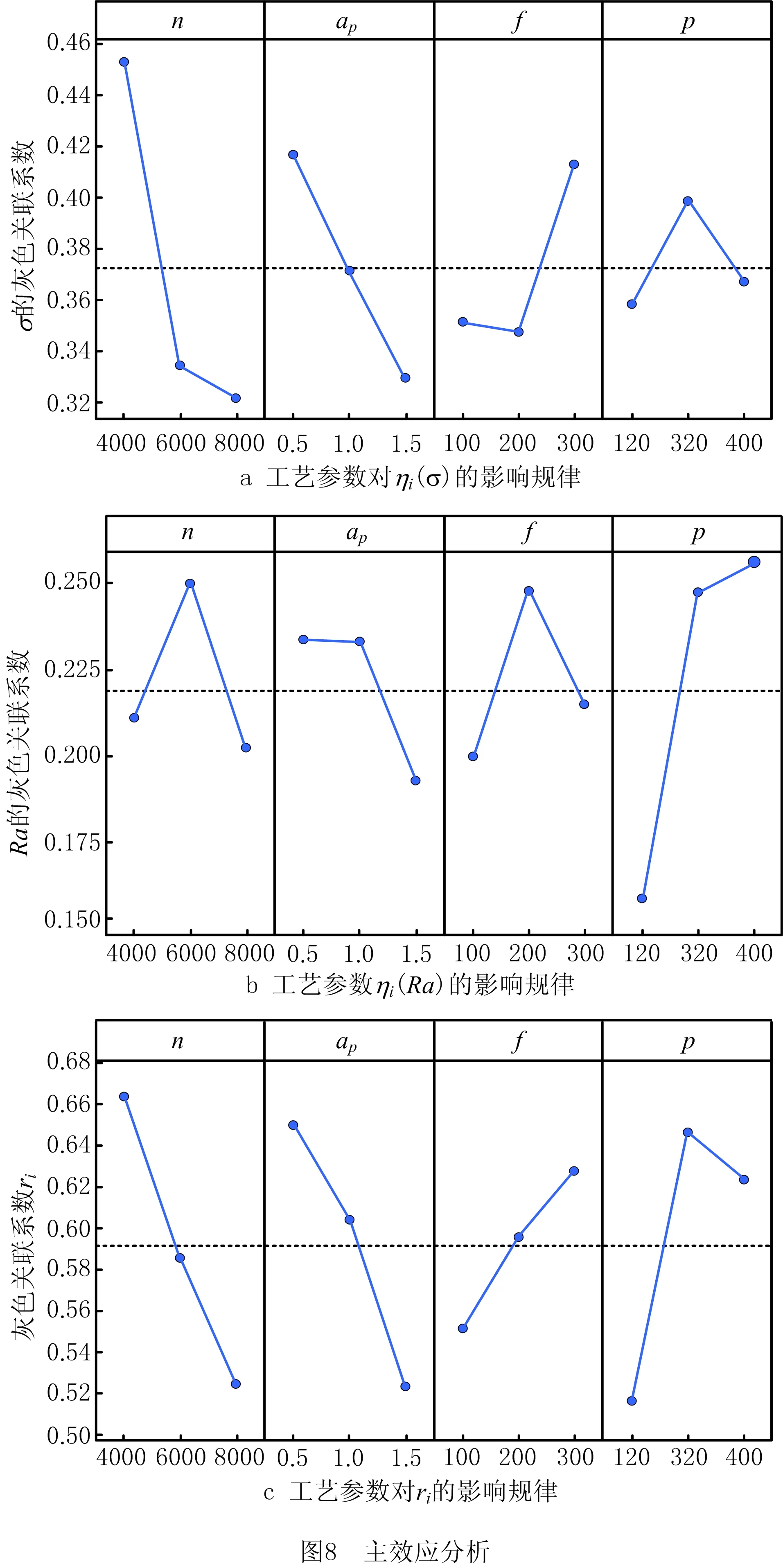
表面残余压应力属于效益型，其灰色关联系数越大，残余压应力越大。故由图8a各参数的斜率可知主轴转速对表面残余应力的影响最大，压缩量次之，进给速度和粒度的影响相对较小；另外，ηi(σ)随主轴转速与压缩量的增大而减小，随进给速度的增大而增大，随粒度的增大先增大后减小。

表面粗糙度为成本型，灰色关联系数越大表面粗糙度值越小。由图8b可知，粒度对应的斜率最大，因此对表面粗糙度影响最大，压缩量次之，主轴转速和进给速度的影响相对较小；ηi(Ra)随主轴转速的增加先减小后增大，随压缩量的增大而增大，随进给速度的增大先减小后增大，随粒度的增加而减小。

由图8c可知，主轴转速、压缩量对灰色关联度影响较大，粒度次之，进给速度的影响最小。其中，灰色关联度随主轴转速、压缩量的增加而减小，随进给速度的增加而增大，随粒度的增加先增大后减小。

根据以上分析可知，最大表面残余压应力和最小表面粗糙度值所对应的最佳水平参数并不一致，因此表面残余应力和表面粗糙度对应的灰色关联系数为参数依赖性响应，而灰色关联度为表面残余应力和表面粗糙度对应的灰色关联系数的加权和，可通过各灰色关联系数随参数的变化判断各参数影响响应目标的规律，灰色关联度则可用于对表面残余应力和表面粗糙度进行整体性参数优化。

4 参数优化及实验验证

4.1 参数优化

采用Minitab中的响应优化器对所建灰色关联度预测模型进行分析，通过分析各工艺参数与表7中的等权关联度得等权模型优化方法如图9a所示，通过分析各工艺参数与表7中的灰色关联度得灰色关联模型优化方法如图9b所示。

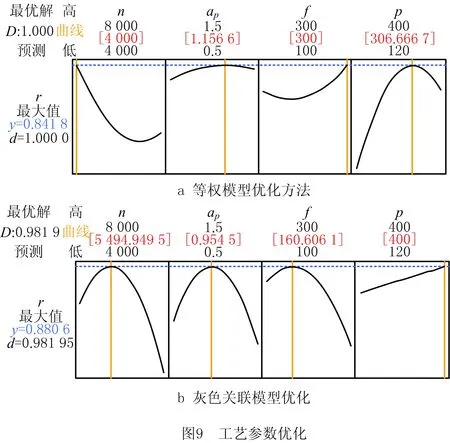
由图9a可知，最优灰色关联度GRG=0.880 6，所对应的工艺参数依次为n=8 000 r/min，ap=1.3 mm，f=300 mm/min，p=298#，因为不存在粒度为298#的百叶轮，所以此处取粒度p=320#。由图9b可知，最优灰色关联度为GRG=0.841 8，所对应的工艺参数依次为n=5 939 r/min，ap=1.2 mm，f=229 mm/min，p=400#。

4.2 实验验证

分别采用等权模型优化方法和灰色关联模型优化方法所得的最佳工艺参数对TC17钛合金叶片进行抛光实验，并对比分析抛光后叶片的表面残余应力和表面粗糙度。抛光后的实验验证数据如表8所示。

表8 实验验证数据

采用两种优化方法抛光的叶片样件如图10a所示，铣削叶片表面的微观形貌如图10b所示，灰色关联模型抛光后叶片表面的微观形貌如图10c所示，等权关联模型抛光后叶片表面的微观形貌如图10d所示。铣削后的表面粗糙度和残余高度较大，采用等权模型和灰色关联模型的优化工艺参数对叶片进行抛光，能够有效去除表面的残留高度，而且采用灰色关联模型的优化工艺参数对表面进行抛光，获得了较好的表面一致性。如表8所示，用等权优化模型得到的最佳参数抛光后，叶片的残余压应力较大，然而粗糙度相对较大，为0.429 μm>0.4 μm。根据工艺参数的稳定域划分所确定的最优区间(如表5)对两种优化方法所得的最优参数进行判断，灰色关联模型优化方法所得到的最优参数均位于最终优选区间，而等权模型的优化方法所得的最优主轴转速、进给速度、压缩量不在最终优选区间。因此，灰色关联优化模型所得的最优参数抛光叶片表面的粗糙度与残余应力更满足工艺要求。

残余应力沿叶片深度方向的分布如图11所示，根据等权模型和灰色关联模型所得的最优参数，比较抛光后残余应力沿深度的分布情况。采用等权模型所得优化参数进行抛光，表面残余压应力为391.4 MPa，大于灰色关联模型所得优化参数抛光的表面残余应力337.5 MPa。采用等权模型的优化参数进行抛光，残余应力的影响深度为20 μm，采用灰色关联模型的优化参数进行抛光，残余应力的影响深度为30 μm。因此，采用灰色关联模型所得的最优参数进行抛光对抛光面残余应力的影响深度更大，当深度达到140 μm时，残余应力趋于稳定。

5 结束语

本文通过对TC17叶片进行抛光实验，分析工艺参数的敏感性、划分稳定域，并确定最优参数区间。分别采用等权模型和灰色关联模型优化百叶轮叶片的抛光工艺参数，结合稳定域划分所确定的最优参数区间，对两种模型的可靠性进行了比较分析，实验结论如下：

(1)对比分析钛合金叶片铣削与抛光后表面微观形貌、粗糙度和残余应力，可知抛光能够去除铣削残留高度，降低粗糙度值，导致表面残余压应力减小。

(2)单因素实验分析可知，粗糙度随各参数的增加先减小后增大；表面残余压应力随主轴转速、压缩量的增大而增大，随进给速度、粒度的增大而减小。

(4)通过残余应力对工艺参数的相对灵敏度分析得Sσ′(n)=0.461 9，Sσ′(ap)=0.260 1，Sσ′(f)=0.152 0，Sσ′(p)=0.043 8，可知残余应力对主轴转速的变化最敏感，压缩量和进给速度次之，对粒度的变化最不敏感。

(5)通过优选粗糙度与残余应力的工艺参数区间，可得主轴转速、压缩量、进给速度和粒度的最终优选区间分别为5 000 r/min～6 000 r/min，0.75 mm～1.0 mm，150 mm/min～300 mm/min，260#～400#。

(6)采用等权模型优化方法得最佳工艺参数为n=8 000 r/min，ap=1.3 mm，f=300 mm/min，p=320#；采用灰色关联模型优化方法得最佳工艺参数为n=5 939 r/min，ap=1.2 mm，f=229 mm/min，p=400#。

(7)采用等权模型优化方法得最佳工艺参数抛光钛合金叶片，叶片表面的残余应力为391.4 MPa，粗糙度为0.429 μm>0.4 μm；采用灰色关联模型优化方法得最佳工艺参数抛光钛合金叶片，叶片表面的残余应力为337.5 MPa，粗糙度为0.372 μm。灰色关联模型优化方法所得的最佳参数均位于稳定域划分所得的最优区间内，在保证粗糙度满足要求的同时，可以保留较大的表面残余压应力。